快速独立分量分析法识别结构模态参数研究*
2016-09-21刘文波常军胡皞巩文龙
刘文波 常军 胡皞 巩文龙
(苏州科技学院土木工程学院, 苏州 215011)
快速独立分量分析法识别结构模态参数研究*
刘文波常军†胡皞巩文龙
(苏州科技学院土木工程学院, 苏州215011)
采用快速独立分量分析(FastICA)算法,快速、准确地识别结构模态参数.该算法以模态响应之间的独立性为依据构建出目标函数,并以此目标函数为基准采用ICA算法对结构输出信号进行分离,而得到结构振型向量.进而通过单模态识别技术-希尔伯特(Hilbert)变换,识别出结构的频率和阻尼比.最后通过白噪声激励下六层框架结构的模态参数识别,验证了快速独立分量分析算法识别结构模态参数的可行性和鲁棒性.
快速独立分量算法,模态参数识别,模态响应,目标函数,希尔伯特变换
引言
模态分析是依据输入和输出响应,采用不同的参数识别方法,获得系统的固有频率、模态阵型和阻尼等模态参数,属于系统识别的重要部分.传统的模态识别方法需要根据系统激励信号和响应信号求出频响函数进行参数识别.但是,由于环境条件的复杂多变和实际结构复杂程度的诸多限制,往往很难准确测得激励和理想的结构响应信号.因此,仅依靠系统输出响应的无监督参数识别方法显示出了独特的优越性.盲源分离技术(Blind Source Separation, BSS)作为无监督的参数识别技术,逐渐成为研究的热点.
独立分量分析(Independent Component Analysis, ICA)属于盲源分离的一种,是指在输入信号未知或不可观测,并且混合系统特性也未知或仅知其少量先验知识(如循环平稳性、非高斯性等)时,仅从观测到的输出信号中提取、恢复出无法直接观测的各个输入信号的过程[1-3].与其它时域方法相比,该技术无需对响应数据进行预先处理,提高了参数识别的精度,计算更加简便.文章对ICA进行模态识别的相关理论和识别过程进行了详细描述,并用六自由度框架验证方法的可行性及良好的抗噪性能.
1 ICA的理论基础
1.1ICA问题的描述
考虑混叠信号系统:
X(k)=AS(k)+N(k)
(1)其中,X(k)∈RM,S(k)∈RN分别表示M维观测信号矢量和N维未知输入信号矢量,N(k)∈RM为M维加性观测噪声矢量,A∈RM×N为未知混合矩阵.ICA的实质在于寻找一个适当的分离矩阵B,通过分离矩阵从观测信号X(k)中恢复输入信号S(k),即Y(k)=BX(k),Y(k)为输入信号的估计矢量[4-6].
1.2ICA的基本假定
由于输入信号和混叠系统未知,如果缺少其它的先验知识,仅仅依靠观测信号很难将输入信号恢复.因此,为了使问题得到解决,根据存在的实际情况,对该算法提出几点假定[7-8]:
(1) 输入信号S(k)各分量si(k)为零均值的平稳随机信号,且分量相互独立;
(2) 混合矩阵A为列满秩矩阵(即A-1存在),通常假定A为方阵;
(3) 为了避免多个信号混合后成为无法分离的高斯信号,假定输入信号最多只有一个高斯信号.
1.3优化判据
ICA算法是一种寻求最优解的过程,即寻找与各输入信号最逼近的独立成分值.因此,ICA主要的两个方面包括优化判据和寻优算法.优化判据即根据各成分独立性判断的不同方面,选择最优的目标函数.函数的概率密度是最基本的优化判据,但是实际应用时概率密度函数是未知的而且一般很难进行估计,因此大多通过其它途径解决.这里采用的是信息理论中的负熵判据[9-10].
当信噪比较高时,输入和输出间互信息量的最大化表明二者的信息冗余量达到最小,即各输出间互信息量最小,也就是负熵最大,从而保证各输出量间的统计独立.
负熵表示与变量密度具有相同均值、方差的高斯变量密度的非负的K-L距离,且对坐标的可逆线性变换具有不变性,定义为:
(2)
式中,ki是正常数;v为一个具有零均值和单位方差的高斯随机变量;yi是具有零均值和单位方差的输出变量;E(·)为均值运算;G(·)种形式的非线性函数.
中心极限定理表明,多个独立随机变量的和比单个信号更接近高斯分布.因此,当负熵最大时分离结束,此时y的非高斯性最强.
1.4快速独立分量分析(FastICA)
快速独立成分分析(FastICA)是一种无监督的盲信号分离算法.该算法基于非高斯性最大化原理,使用固定点迭代理论寻找输入信号非高斯性最大的估计矢量,是一种进行ICA处理的快速、效算法[5,11].
(1) 预处理数据
一般所测得的响应数据都具有一定的相关性,为了保证算法的收敛性和提取独立分量过程的简化,通常要对采集的数据进行预处理.预处理的方法有主成成分分析(PCA)、白化(球化)、模型降维、小波包变换、稀疏变换等.文章主要采用白化进行预处理,白化是对信号施加一个线性变换,使其变为具有单位方差且互不相关的白色信号的过程[6-7].
对观测信号X(t),寻找一个线性变换,使X(t)投影到新的子空间后变为白化信号:
Z(t)=UX(t)
(3)
式中,U为白化矩阵,Z(t)为白化后的信号.
白化矩阵可以根据特征值分析由下列公式得出:
U=Λ-1/2ψT
(4)
式中Λ=diag[λ1,λ2,…,λN],ψ=[l1,l2,…,lN].λi表示观测数据x(t)的协方差矩阵RX=E{X(t)XT(t)}对应的最大特征值,li为相应的特征向量.
(2) 盲源分离
寻找分离矩阵w,使得分离出的估计信号y=wX(t)能达到最大函数值.用牛顿迭代法求解目标函数的最优解,算法的迭代公式为
(5)
(6)
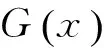
(3) 分离步骤
步骤一:令n=0,对权值向量w(0)进行初始化;
步骤二:调整更新w,w(n+1)=E{Xg(wT(n)X)}-E{g′(wT(n)X)}w(n);
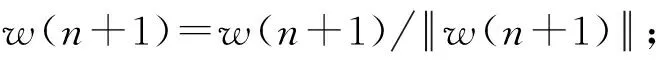
在第三步调整权值时,需要利用期望值.实际计算中,采用样本平均值来简化代替.理论上要求所有样本参与期望值的求解运算,但是这样会导致很大的计算量.因此,每次计算可以随机提取一段长度适中的数据进行平均值的计算,要求提取数据的位置尽可能的分散,其长度要依据迭代算法的收敛效果进行调整.

(7)
(8)
2 正则坐标和独立分量
多自由度运动方程:
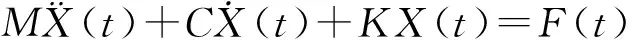
(9)
其中M、K、C、X(t)分别是系统的质量矩阵,刚度矩阵,阻尼矩阵,外力向量和位移坐标.
位移坐标可以用正则坐标和阵型向量表示为:
=Φq(t)
(10)
其中:Φi、wi、ωDi、ξ为第i阶模态振型向量、固有频率、阻尼频率、阻尼比;Φ、q(t)为振型矩阵和正则坐标向量.
正则坐标映射采用的是动力反应的振型叠加法.当不同正则坐标间的振动频率不相等时,对应的正则坐标可以看做统计独立的源信号[13].结合ICA分离原理,把正则坐标看作时间响应序列的一种特殊的输入信号,即结构响应是由正则坐标按振型矩阵线性叠加而成的.将结构自由振动的振型分解看作是一个盲分离问题,从结构的响应中分离得到混合矩阵和分离矩阵Φ-1,其逆矩阵为振型矩阵,从而利用傅里叶变换 (FT)、希尔伯特变换 (HT)或对数变换(LT)进行结构的模态参数识别.
3 数值模拟
建立六层框架模型的数值模型,如图1所示.采用瑞利阻尼模型,并由质量和刚度矩阵得到结构的理论参数值,模型特性如表1所示.以自由响应为研究对象,利用ICA直接从结构振动响应信号中得到结构的模态坐标分量并进行结构振型的估计,再结合HT从单一正则坐标分量中计算出结构系统的固有频率和阻尼比.
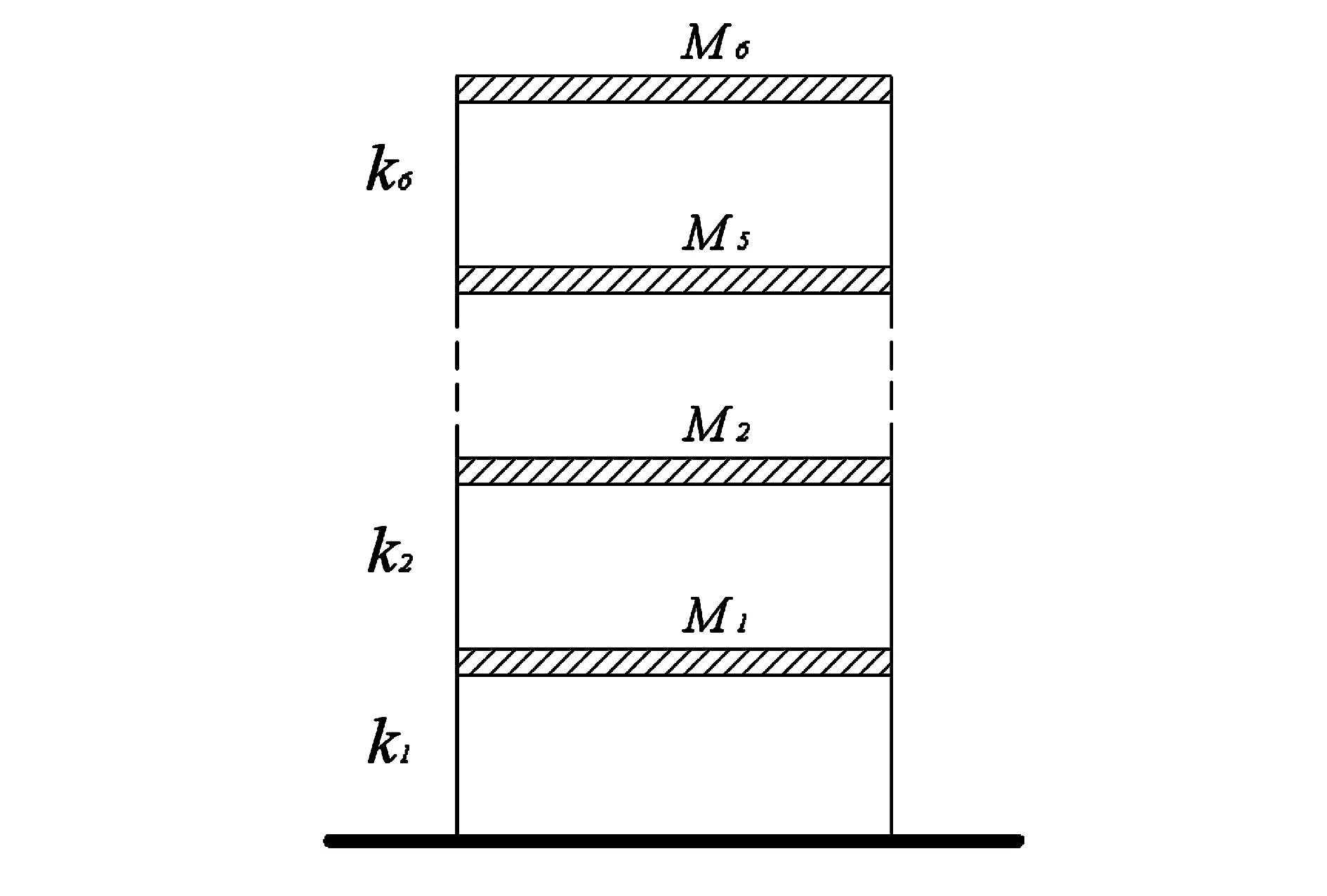
图1 六层框架模型
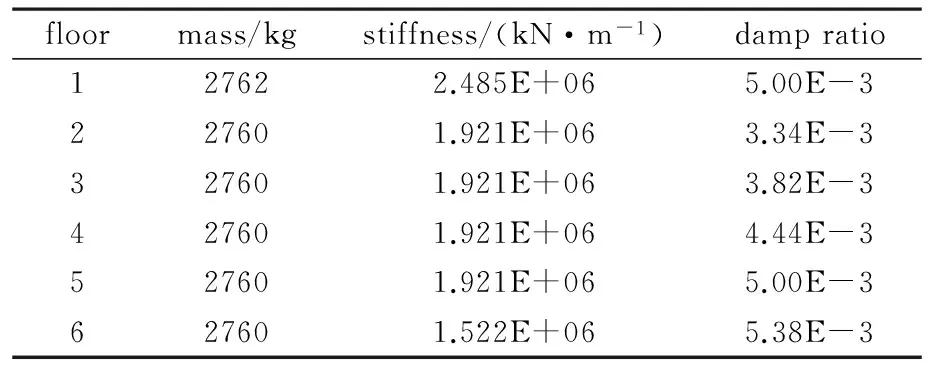
floormass/kgstiffness/(kN·m-1)dampratio127622.485E+065.00E-3227601.921E+063.34E-3327601.921E+063.82E-3427601.921E+064.44E-3527601.921E+065.00E-3627601.522E+065.38E-3
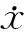
图2 位移响应曲线Fig. 2 Displacement response curves
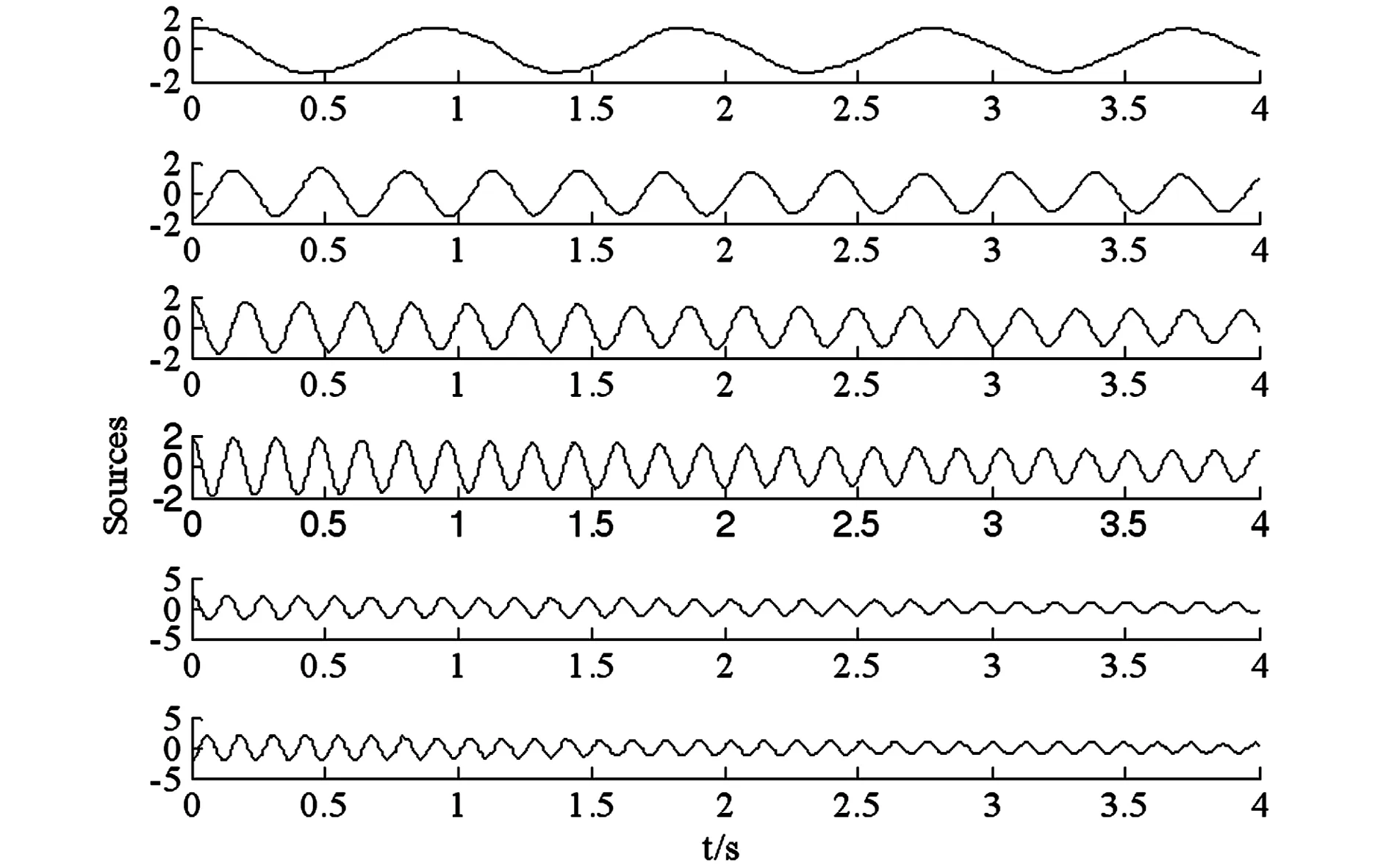
图3 模态响应时程曲线Fig. 3 Modal response time-history curves
比较图3和图4可以看出,FastICA算法识别出的时程曲线与实际输入信号的时程曲线之间基本没有差别,只是二者间的顺序不同,而且某些信号还存在相位角和幅值不同的问题.但是这些不确定性属于算法固有的特性,并不影响振型的提取和模态参数的识别.因为可以依据模态的相关知识确定与分离信号相对应的信号源,进一步处理分离的独立分量.
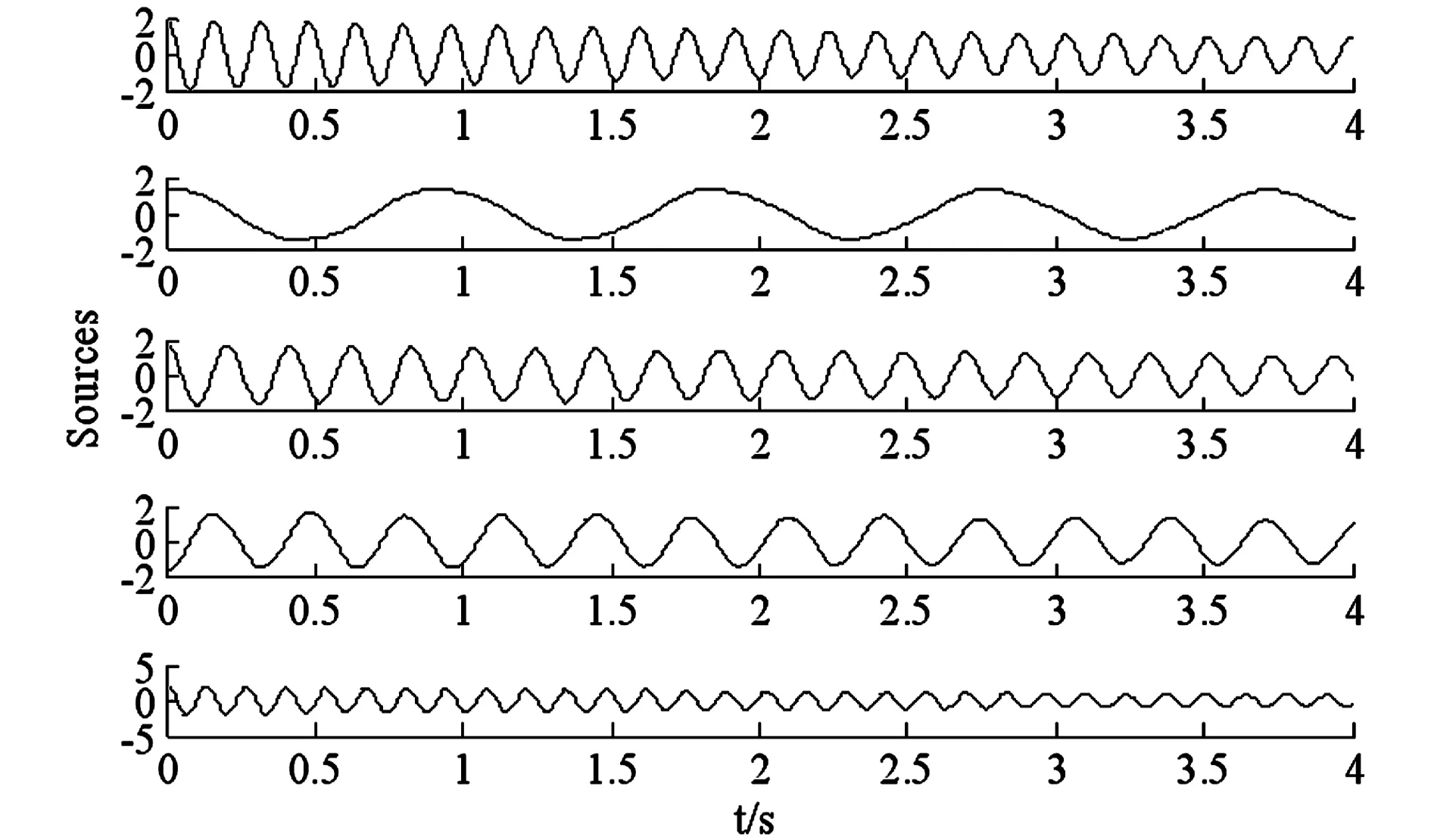
图4 Fast-ICA识别的时程曲线Fig. 4 Time-history curves identified by FastICA
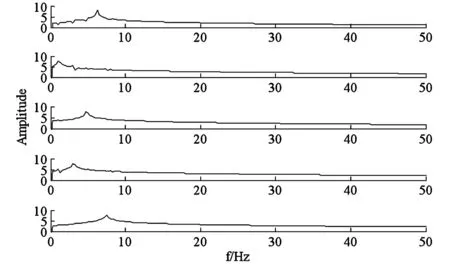
图5 对应的幅频曲线Fig. 5 Amplitude-frequency curves
FastICA识别的原输入信号是自由衰减的简谐振动,对应于各阶模态的正则坐标.因此,可以直接利用Hilbert变换相应的相位角和对数幅值曲线,采用最小二乘拟合得到曲线斜率,进一步计算得到结构的频率和阻尼比.为验证本文方法的鲁棒性和有效性,按照公式(11)以信号能量为基准附加一定比率的白噪声,并和传统频域识别方法峰值法(pick-peaking,PP)进行比较.
(11)
式中,RMS代表信号的标准差值.表2给出了对应工况下的识别结果.
FastICA识别模态振型的准确度,可以利用识别振型与结构模态振型理论解的模态置信度(Modal Assurance Criterion)准则来描述,其定义为:
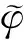
(12)式中为理论振型,φ为识别振型.MAC值介于0和1之间,其值越接近1意味着两个模态振型之间的相关性越好.框架各阶对应的振型图如图6所示.
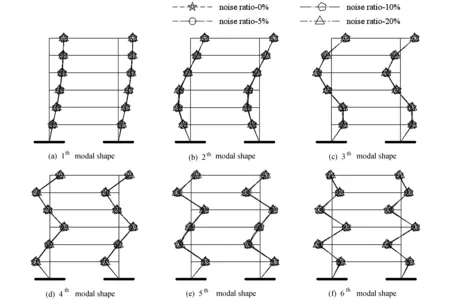
图6 模态振型Fig. 6 Modal shape
从表2的识别结果中可以看出:(1)在该算例工况中,FastICA对于低频的识别比PP法具有相对较高的精度,有一定的抗噪性,但不如PP法抗噪性强;(2)在无噪和有噪声条件下,ICA所识别的模态振型与振型理论解的MAC值均在99%以上,白噪声对振型识别结果不产生明显的影响;(3)无噪声时频率结果的识别值与理论解基本一致,阻尼比识别结果第2阶的误差稍大,也仅为3.5%;(4)加入噪声后,各阶频率和阻尼比的识别误差逐渐增大.噪声为10%时,频率误差最大为8.41%,阻尼比最大误差为11.83%,表明算法具有较好的稳定性.
4 结论
1) 独立分量分析算法在无噪声条件下,模态参数识别结果与理论值基本一致,表明了算法进行结构参数识别的可行性和有效性;
2) 算法对低频的识别比高频精度高且具有一定的抗噪性能,可以用于实际环境下工程结构的模态参数识别及作为结构损伤识别、结构状态评估等健康监测有效的输入参数;
3) 算法的局限性在于仅适用于阻尼比为1%以下的低阻尼结构,且要求结构传感器数量远大于或至少等于结构的活性模态.
1毛欣,徐慨,刘杰. 盲信号分离技术现状与发展动态. 通信技术,2013,46(8):24~26 (Mao X, Xu k, Liu J. Present situation and development of blind signal separation technology.CommunicationsTechnology, 2013,46(8):24~26 (in Chinese))
2Hyvärinen A, Oja E. Independent component analysis: Algorithms and applications.NeuralNetworks-Oxford, 2000,13:411~430
3Antoni J. Blind separation of vibration components: principles and demonstration.MechanicalSystemsandSignalProcessing, 2005,19:1166~1180
4McNeill S. Modal identification using blind source separation techniques[PhD Thesis]. Houston, University of Houston, 2007
5静行,袁海庆,赵毅. 基于独立分量分析的结构模态参数识别. 振动与冲击,2010,29(3):137~141 (Jing H, Yuan H Q, Zhao Y. Structural modal parameter identification based on independent component analysis.JournalofVibrationandShock, 2010,29(3):137~141 (in Chinese))
6张晓丹,姚谦峰. 基于盲源分离的结构模态参数识别. 振动与冲击,2010,29(3):150~153 (Zhang X D, Yao Q F. A modal identification method based on fast ICA.JournalofVibrationandShock, 2010,29(3):150~153 (in Chinese))
7Yang Y, NAgarajaiah S. Time-Frequency blind source separation using independent component analysis for output-only modal identification of highly damped structures.ASCEJournalofStructuralEngineering, 2013, 139:1780~1793
8张晓丹. 基于盲源分离技术的工程结构模态参数识别方法研究[博士学位论文]. 北京:北京交通大学,2010 (Zhang X D. Study on structural modal identification using blind source separation techniques[PhD Thesis]. Beijing: Beijing Jiaotong University, 2010 (in Chinese))
9Zang C, Friswell M I, Imregun M. Structural damage detection using independent component analysis.StructuralHealthMonitoring, 2004, 3:69~83
10Kerschen G, Poncelet F, Golinval J C. Physical interpretation of independent component analysis in structural dynamics.MechanicalSystemsandSignalProcessing, 2007,21(4):1561~1575
11Chao J C, Douglas S C. A simple and robust FastICA algorithm using the Huber M-estimator cost function. ICASSP2006. Toulouse, France. 2006:14~19
*The project supported by the Jiangsu Province Natural Science Foundation (BK20141180) and the Scientific Research Foundation of University of Science and Technology of Suzhou(XKZ201304)
† Corresponding author E-mail: changjun21@126.com
12 August 2014,revised 2 October 2014.
STUDY ON FASTICA IDENTIFYING STRUCTURAL MODAL PARAMETERS*
Liu WenboChang Jun†Hu HaoGong Wenlong
(SchoolofCivilEngineering,UniversityofScienceandTechnologyofSuzhou,Suzhou215011,China)
This paper presented a structural modal parameters identification by Fast Independent Component Analysis (Fast ICA) rapidly and accurately. The method builds the objective function based on the independence between the modal responses, and separates the structural output signals by Fast ICA based on the objective function, and gains the structural modal shape vectors. Then structural frequencies and damping ratios are gained by Hilbert transform, a single mode analysis technical. Finally, the efficiency and robust of structural modal parameters identification by Fast ICA presented herein was verified by a six-story frame structure.
fast independent component analysis,modal parameters identification,modal response,objective function,Hilbert transform
E-mail: changjun21@126.com
10.6052/1672-6553-2016-01
2014-08-12收到第1稿,2014-10-02收到修改稿.
*江苏省自然科学基金项目(BK20141180)、苏州科技学院科研基金项目(XKZ201304)
