基于数字工业摄像的非接触式纯弯曲梁正应力测量

刘　洋，钱仁军，张卫峰，资新运，何　健

(1．军事交通学院 基础部，天津 300161； 2.军事交通学院 研究生管理大队，天津 300161；2．军事交通学院 军用车辆系，天津 300161)



● 基础科学与技术Basic Science & Technology

基于数字工业摄像的非接触式纯弯曲梁正应力测量

刘洋1，钱仁军2，张卫峰3，资新运3，何健2

(1．军事交通学院 基础部，天津 300161； 2.军事交通学院 研究生管理大队，天津 300161；2．军事交通学院 军用车辆系，天津 300161)

提出一种基于数字工业摄像的纯弯曲梁正应力测量方法，通过CCD工业相机采集弯曲梁应变前后表面的图像信号，对应变前后的图像进行二维相关计算和基于梯度法的亚像素位移计算，得到弯曲梁表面的应变位移量，进而计算出弯曲梁正应力。搭建了数字工业摄像实验系统，设计了与电阻应变片法测正应力的对比实验，并对结果进行了误差分析。结果表明：数字工业摄像的正应力测量精度在5%以内，能够适用于弯曲梁表面微小应变的位移测量。

光学测量；正应力测量；数字工业摄像；数字散斑相关技术；梯度法

数字工业摄像系统通过CCD工业相机，采集弯曲梁在应变前后的表面图像，将弯曲梁上因载荷所产生的应变量转换为表面散斑图像的位移量。然后通过数字散斑相关技术(digital speckle correlation method，DSCM)，计算得到表面的应变位移，从而最终得到正应力值。数字散斑相关技术是近年来发展的一种高精度的物体表面和内部位移与应变的测试方法，是对全场位移和应变进行量化分析的光测实验力学方法。它的基本原理是通过比较试件变形前后所采集散斑图的变化，来获得物体位移和应变场等力学信息[1]。该方法系统简单，抗干扰能力强，并且具有非常高的精度。

赵健[2]将数字散斑相关方法在材料变温实验和木材断裂力学实验中进行了应用，探讨了数字散斑相关方法在实际应用中的正确性、适用性和通用性。苑苗苗[3]基于DSCM测量方法对两种粒径沥青混合料的疲劳变形局部化特征进行了研究，对材料疲劳断裂过程进行了实验观察。章超等[4]运用数字散斑相关方法的原理，对泡沫铝冲击变形过程的高速摄影图像进行处理，研究了高速冲击载荷下泡沫铝的全场应变及其变化趋势。

本文将其应用在纯弯曲梁正应力测量的力学实验中，并与传统电测法实验进行了对比分析。

1　系统设计

数字散斑相关法的核心就是应变前后两幅图像上对应点的匹配，其基本原理如图1所示。在两幅图像上，同一点位移前后子区的灰度值基本不变，因此子区灰度值可以作为图像特征进行匹配。DSCM便是通过分析应变前后采集的两帧物体表面散斑图像灰度来获得物体的应变信息。

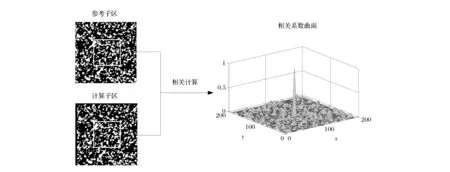
图1　数字散斑相关法原理

在数字散斑场中，由于散斑点具有随机性，每点周围区域的散斑分布规律各不相同，因此可在应变前图像(参考图像)中选择以P0为中心、大小为(2M+1)×(2M+1)的像素子区。通过相关计算，在应变后图像(目标图像)中搜索相似度最大的子区，得到与相对应的子区中心点P1，进而获得应变位移信息。文献[5]中列举的函数有10种，应用最为广泛的是标准化协方差函数，本文采用标准化协方差函数的平方形式作为相关函数：

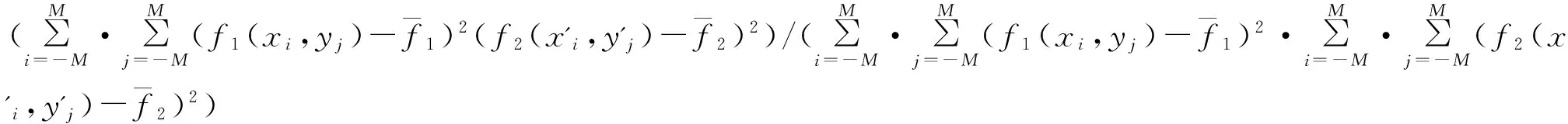
(1)

由于弯曲梁表面实际应变位移很小，整像素级别的测量精度不足以满足实际测量需求，因此，在整像素搜索的基础上，对表面位移进行亚像素搜索，从而得到更高精度的测量值。

文献[6]对3种常用的亚像素位移测量算法进行了研究，并用数值模拟进行了比较。结果显示，牛顿-拉普斯法计算精度最高，但易受噪声影响；曲面拟合法具有较大不确定性，精度不高；梯度法具有较高的精度，同时具有较强的抗噪性。本文采用梯度法作为亚像素位移测量算法。

假设图像子区做微小位移时，若子区足够小，则图像子区运动可近似为面内刚体运动，此时有

(2)

式中：u和v分别为与x、y方向上的整像素位移；

Δu、Δv为相应的亚像素位移。

对式(2)进行泰勒展开，并舍弃高阶小量，得

g(xi+u+Δu,yj+v+Δv)≈g(xi+u,yj+v)+Δu·gx(xi+u,yj+v)+Δv·gy(xi+u,yj+v)

(3)

式中gx和gy为子区一阶梯度。

选择效果较好的Barron算子：

(4)

将式(3)带入最小平方距离相关函数，所求亚像素位移Δu、Δv将使其取得驻值，即

C(Δu,Δv)=∑∑(f(x,y)-g(x+u+Δu,

y+v+Δv))2

(5)

(6)

(7)

结合以上两步位移计算，可以得到弯曲梁表面任一点的像素位移量，通过标定关系，可以得到其实际应变位移量。

根据材料力学中纯弯曲梁的平面假设：变形前原为平面的梁横截面变形后仍保持为平面，仍然垂直于变形后的梁轴线，可得出弯曲梁受力变形(如图2所示)。

(a)原理结构

(b)实际受力变形图2　纯弯曲梁受力变形

图中，ρ为中性层的曲率半径，纯弯曲梁变形前，A、B、C、D是在其表面确定的4个点，AB、CD分别垂直于梁轴线，ABCD构成一个矩形。变形后，运用数字散斑相关法，分别搜索到A、B、C、D的匹配点，从相似三角形可知：

(8)

从而求得

(9)

根据材料力学，在纯弯曲条件下，任意纵向纤维的正应力与它到中性层的距离成正比，求出正应力为

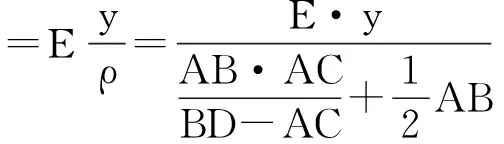
(10)

式中：σ计为计算得出的正应力值；E为弯曲梁的弹性模量；y为所求应力点至中性层的距离。

2　实验验证

为验证本文实验方法，搭建高精度的纯弯曲梁正应力测量实验平台(如图3所示)。通过拉力轮对弯曲梁添加载荷，载荷F可由标准力传感器测出。在梁的表面贴有电阻应变片，应变值由XL2118C型力&应变综合参数测试仪读出。弯曲梁正对面搭建了Pike-F032bCCD工业相机，采集图片信息为640×480pixel，并通过数据线传输给工业计算机。

测定弯曲梁的原始尺寸，所测结果见表1。

图3　实验平台

应变片至中性层的距离/mmY1-20Y2-10Y30Y410Y520梁的尺寸和参数数值宽度b/mm20高度h/mm40跨度L/mm600载荷距离a/mm125弹性模量E/GPa206

实验中，利用加载系统均匀缓慢地给弯曲梁等增量加载载荷，依次记录各点电阻片的应变值ε。每次加载完毕记录数据后，利用CCD工业相机拍下弯曲梁表面已经变形的数字散斑图。实验数据记录见表2。

表2　各测点实验记录数据

每次加载载荷产生的标准正应力为

(11)

式中：M为载荷的力矩；Iz为惯性矩。

载荷F每增加200 N，分别用两种方法测量一次各测点的正应力值。

(1)电测法。根据材料力学中单向应力状态的胡克定律，求出各点的实验应力为

σi实=Eεi实

(12)

式中εi为各应变片测量的应变值，i=1，2,3,4,5。

(2)数字工业摄像。以序列为0的散斑图为参考图像，在参考图像中选择A、B、C、D四点为参考点，坐标分别为(100,100)、(380,100)、(100,540)和(380,540)。以A、B、C、D为中心，选择窗口大小为41×41 pixel的子区，作为参考子区。将参考图像分别与不同载荷下的应变散斑图像(目标图像)进行相关计算，求出A、B、C、D四点所对应的应变位移点，通过像素位移值与实际位移值的标定关系，进而计算出中性层曲率半径ρ。

以载荷F=2 200 N时为例，对参考图像和所采集的应变散斑图像进行相关计算，得出参考图像中A、B、C、D四点在应变散斑图像中的对应点(如图4所示)。

(a)A点在目标图像上的搜索结果

(b)B点在目标图像上的搜索结果

(c)C点在目标图像上的搜索结果

(d)D点在目标图像上的搜索结果图4　各点的相关计算结果

由图4可知，在载荷为2 200 N的作用下，将像素位移值转换成实际位移值，AB、AC、BD实际距离均可求出，带入式(10)，得到各应变片测点处纯弯曲梁正应力的计算值σi计。以1号应变片为例，最终实验结果和计算误差见表3。

表3　Y1测点实验测量数据

从表3可获得，1号测点处正应力值与所加载荷的关系(如图5所示)。

图5　1号测点正应力与所加载荷关系

采用增量法分析，即

(13)

可得到1号测点数据(见表4)。

表4　Y1测点增量法实验数据

表5　各测点增量法平均值数据

由表5可知，各测点正应力平均值与各测点至中性层的距离的关系如图6所示。

图6　各测点正应力平均值与测点至中性层距离关系

由表5和图6可知，数字摄像法与电测法测量精度已经比较接近，并且结论一致：当某一测点至中性层距离不变，该测点处正应力值与所加载荷成正比；当所加载荷增量为等载荷增量，弯曲梁各测点处正应力值与各测点至中性层的距离成正比。

3　结　语

本文针对纯弯曲梁正应力的测量需求，提出了基于数字工业摄像的弯曲梁正应力测量方法，搭建了用于测量正应力的实验系统，并对其进行了理论分析和实际测量实验。

本文实验系统可以调整相机与梁的距离位置，从而调节相机的放大倍数，满足梁不同大小的应变位移测量需求。当测量微小应变时，所需测量的应变位移值很小，较小的位移测量偏差就会对测量精度产生较大影响，故需要较大的放大倍数，以保证足够的测量精度；当测量较大应变时，

所需测量的应变位移值很大，较小的位移测量偏差不会对测量精度产生太多影响，故需要较小的放大倍数，以保证足够的测量范围。

随着CCD工业相机的不断发展，本文方法的测量精度也会不断提高，可根据测量精度需求配置设备，系统结构简单，为纯弯曲梁的正应力测量提供了新方法，对梁的大应变位移测量具有一定的指导意义。

[1]孟力波.数字散斑相关方法的研究和应用[D].北京:清华大学,2005.

[2]赵健.数字散斑相关方法及其在工程测试中的应用研究[D].北京:北京林业大学,2014.

[3]苑苗苗.基于数字散斑相关方法的沥青混合料疲劳破坏机理研究[D].广东:华南理工大学,2013.

[4]章超,徐松林,王鹏飞,等.基于数字图像相关方法对冲击载荷下泡沫铝全场变形过程的测试[J].实验力学,2013,28(5):629-634.

[5]MA S P, JIN G C. New correlation coefficients designed for digital speckle correlation method (DSCM)[C]. Proc. SPIE. 2003,(5058):25-33.

[6]资新运,耿帅,赵姝帆,等.3种亚像素位移测量算法的比较研究[J].计量学报,2015,36(3):260-267.

[7]田莹,苑玮琦.遗传算法在图像处理中的应用[J].中国图像图形学报,2007,12(3):389-395.

[8]刘国华,包宏,李文超.用Matlab实现遗传算法程序[J].计算机应用研究,2001(8):80-82.

[9]潘兵,谢惠民,续伯钦,等.数字图像相关中的亚像素位移定位算法进展[J].力学进展,2005,35(3):345-352.

[10]潘兵,谢惠民,续伯钦,等.面内位移测量的基于梯度的数字图像相关方法[J].光学技术,2005,31(5):643-647.

[11]潘兵，吴大方，谢惠民,等.基于梯度的数字体图像相关方法测量物体内部变形[J].光学学报,2011,31(6):1-7.

[12]米红林.基于数字散斑相关法的岩石材料力学性能的测试[J].应用光学,2013,34(1):123-127.

[13]资新运,耿帅,李永乐,等.应用数字散斑相关的运动轴面位置匹配[J].光学精密工程,2015,23(4):941-948.

[14]资新运,耿帅,赵妹帆,等.数字工业摄像技术用于转轴动态扭矩测量原理的研究[J].中国激光,2015,42(2):1-7.

(编辑：张峰)

Normal Stress Measurement of Non-contact Pure Bending Beam Based on Digital Industrial Photography Technology

LIU Yang1， QIAN Renjun2, ZHANG Weifeng3, ZI Xinyun3, HE Jian2

(1．General Courses Department, Military Transportaion University, Tianjin 300161, China;2.Postgraduate Training Brigade, Military Transportation University, Tianjin 300161, China;3.Military Vehicle Department, Military Transportation University, Tianjin 300161, China)

A new method for measuring normal stress of pure bending beam is proposed. The image signal is obtained by CCD industrial camera, and then the strain displacement is calculated on the surface of the curved beam, and the normal stress of bending beam is calculated. The experimental system of digital industrial camera is set up, and the comparison experiment of the positive stress with the resistance strain gauge method is designed, and the error analysis is carried out. The experiment shows that the accuracy of positive stress measurement in digital industry is less than 5%, which can be applied to the measurement of micro displacement of curved beam.

optical measurement; normal stress measurement; digital industrial photography technology; digital speckle correlation; gradient method

2015-11-12；

2015-12-01．

国家高技术研究发展计划项目(2013AA065303)；国家自然科学基金重点项目(91120306)．

刘洋(1978—)，男，硕士，讲师．

10．16807/j.cnki.12-1372/e.2016.05.022

TP391.41

A

1674-2192(2016)05- 0090- 06