基于神经网络的异步电动机PI控制器参数在线整定

康少华，蒋林飞，张　俊

(1．军事交通学院 军事物流系，天津 300161； 2．军事交通学院 研究生管理大队，天津 300161)



● 车辆工程Vehicle Engineering

基于神经网络的异步电动机PI控制器参数在线整定

康少华1，蒋林飞2，张俊2

(1．军事交通学院 军事物流系，天津 300161； 2．军事交通学院 研究生管理大队，天津 300161)

针对传统异步电动机矢量控制系统PI控制器存在的适应性弱、不能实时进行自适应调节的问题，提出了一种基于神经网络的异步电动机PI控制器参数在线整定的控制策略。实验表明，采用的控制方案可行，在负载转矩突变的情况下具有良好的转速特性，增强了系统的鲁棒性。

异步电动机；矢量控制；神经网络；PI控制

异步电动机结构坚固、工作可靠、易于维护，普遍用于蓄电池叉车、牵引车以及各种电动汽车的电驱动系统。但是，异步电动机的数学动态模型复杂，是一个多变量、高阶、非线性、强耦合的系统，其系统控制复杂。目前，应用较多的控制系统为基于转子磁场定向的矢量控制系统，即模仿直流电机的控制方法，将定子电流分解为转矩电流和励磁电流两部分，独立进行调节控制，从而实现转矩电流与励磁电流的解耦控制。在实际控制系统的设计中，可以对转矩电流分量和励磁电流分量分别进行闭环控制，这样就实现了异步电动机转矩的有效控制。

在传统的异步电动机矢量控制系统中，转矩电流和励磁电流的控制是通过PI调节器实施控制的，PI调节器具有结构简单、控制精度高以及鲁棒性好的特点。但传统的PI控制参数固定，在控制电机的运行过程中，如果电机的参数出现变化(如转子时间常数)，会造成控制精度下降，甚至不稳定。此外，在对异步电动机PI矢量控制进行参数整定过程中，所得的参数值是一定范围内的最优解，而不是全局的最优解，这时需要对PI矢量控制器的参数进行在线整定，以适应这种变化和提高控制精度。现有的将PI矢量控制器与遗传算法、蚁群算法以及粒子群算法等相结合的智能控制方法，在改进PI矢量控制方面取得了一定的优化效果，但都不同程度地存在计算量大、模型复杂、实时性差等问题。因此，本文采用基于PI矢量控制模型的神经网络控制方法，将PI控制的参数作为神经网络的权值，通过对PI矢量控制的神经网络模型进行在线训练，得到PI矢量控制的两个最佳参数，从而实现电机参数随运行时间变化的实时最优控制。

1　矢量控制与数学模型

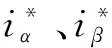
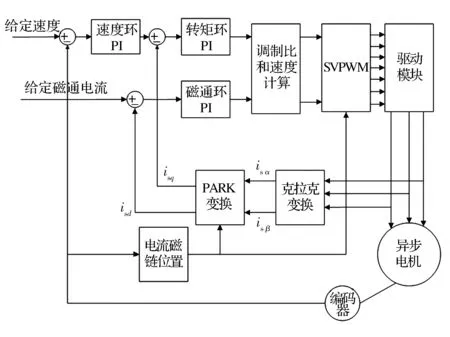
图1　矢量控制系统结构

异步电动机矢量控制的关键在于将异步电动机的数学模型进行一系列坐标变换，最后简化得到易于控制的模型。图1中SVPWM模块用于根据矢量信号跟踪异步电动机的圆形磁场，并发出脉宽信号驱动异步电动机。异步电动机在三相静止坐标系α-β中的数学模型为

(1)

式中：u为定子和转子电压矩阵；R为电阻矩阵；i为定子和转子电流矩阵；er为电磁感应电动势中与角速度ω成正比的旋转电动势；Te、TL分别为电磁转矩和负载阻力转矩；J为机组的转动惯量；L为电感矩阵；pn为电机磁极对数。

异步电动机在两相静止坐标系d-q中的数学模型为

(2)

式中：isd、isq分别为定子d轴电流和q轴电流；ird、irq分别为转子d轴电流和q轴电流；Lm为定子与转子同轴等效绕组间的互感。

在矢量控制系统中，若将d轴取为沿着转子磁链Ψr方向，称作M轴，再逆时针旋转即为T轴。当两相同步旋转坐标系按转子磁链定向时，d轴落在转子磁链矢量Ψr上，而Ψr在q轴的分量为0。异步电动机在两相旋转坐标系M-T下的数学模型为

(3)

式中：Ψr为转子磁链；ism为定子励磁分量；ist为定子转矩分量；Tr为转子时间常数。

2　基于神经网络的PI控制器

当前应用较多的BP神经网络存在收敛速度慢的问题，用作控制器的矢量控制算法时计算量太大，会导致控制的实时性变差。为此本文采用简化的神经网络算法，在保留神经网络控制优良特性的同时减小了计算量，提高了系统控制的实时性。

通用的数字增量式PI控制算法表达式为

Δu(k)=Kp[e(k)-e(k-1)]+KIe(k)

(4)

这种方法理论上可以通过异步电动机矢量控制的模型来建立系统的控制模型，从而计算出KP和KI值。然而，由于异步电动的模型对于异步电动机的描述总是存在误差，导致所得KP和KI不能使PI控制器达到最优的控制性能，所以KP和KI值还得进行在线调整，以使异步电动机的控制系统达到最优的控制性能[2]。

神经网络采用前馈网络模型，并将PI控制器的两个参数KP和KI作为神经网络的连接权值，如图2所示[3]。

策略：延长入射光线与折射光线比，如果折射光线更靠近法线则为会聚是凸透镜，如果折射光线远离法线为凹透镜。

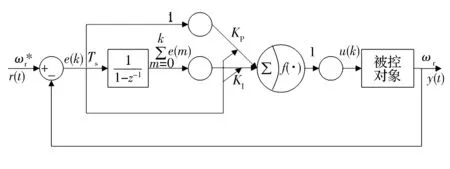
图2　神经网络原理

神经网络用于自动控制具有以下特点：一是神经网络可以处理难以用模型进行精确描述或参数随时变化的系统；二是神经网络的并行计算特性可以实现实时控制；三是神经网络自身可以看作是一个多维的系统，因此可以通过自身的调整去逼近任意的非线性系统；四是神经网络处理信息的能力很强，能够处理大量不同的输入信息[4]。

神经网络算法的实现步骤如下：

(1)给定初始权值：KP=0、KI=0，设e(-1)=0，φ(0)=1。

(2)分别计算误差和学习率。

e(k)=r(k)-y(k)

(3)递归计算权值。

KP(k+1)=KP(k)+μe2(k)yu(k)

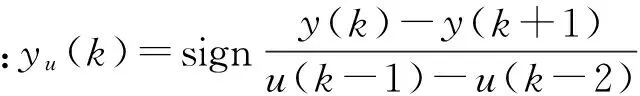
(4)计算神经网络输出。

(5)返回继续执行步骤(2)。

3　实验结果与分析

基于神经网络PI控制器(调节器)的矢量控制系统如图3所示。应用keil软件进行神经网络算法程序编写，测试数据如图4所示。

图3　实验控制器

图4　数据显示界面

实验用异步电动机额定转速为1 200 r/min，额定电流为270 A，额定频率为40 Hz，额定电压为48 V，额定功率为11 kW，互感为Lm=0．172 2 H，漏感为Ls=5．839 mH，转子时间常数为Tr=0.276，转子电阻为Rr=1.25 Ω，电机磁极对数为np=2。

试验中，稳定运行转矩设定为30 N·m，然后突然变为10 N·m，再变为30 N·m，转速设定为1 200 r/min。

当负载转矩为30 N·m时，传统的PI控制电机会出现抖动、转速不稳，响应曲线如图5所示。采用神经网络PI控制后，转速波动幅度减小(如图6所示)。

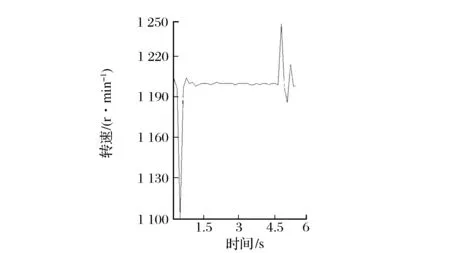
图5　30 N·m时传统PI控制的转速响应曲线

图6　30 N·m时神经网络PI控制转速响应曲线

当负载转矩由30 N·m变为10 N·m时，转速的波动减少了大约35 r/min。在由10 N·m突然变为30 N·m时，转速的波动减少了大约30 r/min，并且在实验时使用神经网络PI控制时的噪声较小，优化效果明显。在这种情况下，神经网络PI控制比传统的PI控制响应快、超调小，具有良好的转速动态性能。

当负载转矩由30 N·m变为50 N·m，再变为30 N·m时，分别得到转速的响应曲线如图7和图8所示。可以看出，在负载转矩较大时神经网络PI控制与传统的PI控制对转速相应的优化上只有5 r/min左右的差距，对转速响应的调节虽然有效果但不明显，这主要是由于在负载转矩较大时，电机的转速响应主要受电机自身的影响，参数的优化已变成次要因素。

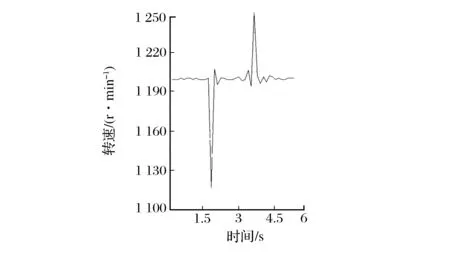
图7　50 N·m时传统PI控制转速响应曲线

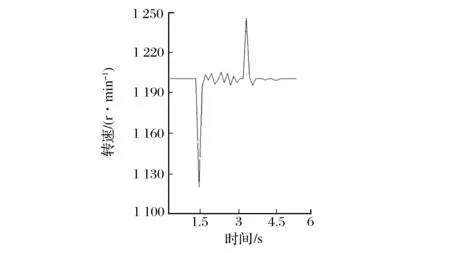
图8　50 N·m时神经网络PI控制转速响应曲线

4　结　语

本文在分析矢量控制理论的基础上，将传统的异步电动机神经网络PI控制方法进行了改进，将转速PI的两个参数选为网络的权值，以输出值和期望值的差值和所设计的神经网络输出的实际值对神经网络进行训练，从而获得PI的最佳参数。这种方法克服了传统神经网络PI控制需要调整的权值多、计算量大的不足，在负载转矩不大时，能够实现快速响应，且超调量和抗干扰能力均优于传统的PI控制。

[1]陈伯时，陈敏逊.交流调速系统[M].3版.北京：机械工业出版社，2013：119-126.

[2]曾喆昭．神经计算原理及应用[M].北京：科学出版社，2012：199-205.

[3]李鹏，王胜勇，卢家斌，等.PI参数混合整定法在闭环矢量控制系统中的应用[J].智能系统学报，2013，8(5)：446.

[4]杨宁，史仪凯，袁小庆，等.基于BP网络横向磁场永磁电机调速系统的设计[J].西北工业大学学报，2011，29(5)：824.

[5]陈伯时.电气传动控制系统调节器的工程设计方法[M]//电力电子与电力传动自动化：陈伯时教授文集．北京：机械工业出版社，2008：40-61.

(编辑：史海英)

The Self-tuning Method of Asynchronous Motor PI Adjuster Parameters Based on Neural Network

KANG Shaohua1, JIANG Linfei2, ZHANG Jun2

(1．Military Logistics Department, Military Transportation University, Tianjin 300161, China；2．Postgraduate Training Brigade, Military Transportation University, Tianjin 300161, China)

Considering that traditional PI adjuster in asynchronous motor vector control system is poor at adaptation and cannot be adaptively adjusted, this paper proposes the online tuning control strategic of asynchronous motor PI adjuster parameters based on neural network. The experiments show that the control adopted is feasible and has a good speed response on a sudden load torque change, which enhances the system robustness.

asynchronous motor; vector control; neural network; PI adjuster

2015-12-21；

2016-01-14．

康少华(1959—)，女，教授．

10．16807/j.cnki.12-1372/e.2016.05.009

TM301．2

A

1674-2192(2016)05- 0036- 04