差异产品的最优定价决策

李梅英，赵　晗， 陈　静，李亚玲

(1.军事交通学院 基础部，天津 300161； 2.军事交通学院 学员旅，天津 300161)



● 基础科学与技术Basic Science & Technology

差异产品的最优定价决策

李梅英1，赵晗2， 陈静1，李亚玲1

(1.军事交通学院 基础部，天津 300161； 2.军事交通学院 学员旅，天津 300161)

针对差异产品定价问题，考虑有一个制造商和两个零售商组成的供应链系统，该制造商生产两种差异产品并把这两种产品分别批发给这两个竞争的零售商，然后再由他们销售给顾客。利用博弈论的方法在两种不同情形下探讨了该供应链中每一个参与企业的定价决策，研究了各参与企业在面临变化的环境时的决策行为，分析了参数对于各参与企业的决策及收益的影响，可为企业决策提供一定的理论依据。

定价决策；博弈论；差异产品

近年来，许多制造商通过分离他们的基本产品的一些关键属性 (如颜色、外观形状、附加功能等)来扩大产品的种类，以此来赢得更多的产品市场份额。Ho等[1]指出许多公司每年都以高于10%的速度扩大自己产品的种类。尽管增加产品的种类能得到消费者的极大欢迎，但是这同时也给零售商带来了许多新的挑战。首先，同一种产品的不同类型(如不同颜色、不同外观形状、不同附加功能等)之间在某种程度上存在着需求相互替代的关系，在这种情形下零售商该如何决定产品的分类以最大化自己的销售利润？其次，对于给定的产品种类零售商该如何决策每种产品的订货量来最大化自己的利润？第三，当不同类型的产品可以产生需求互相替代时，零售商如何通过调整零售价格来最大化自己的利润？对于存在零售竞争的零售商来讲，既不能把自己所销售的产品价格定得过高，否则，市场对自己所售产品的需求会转移到竞争者所售的产品上去；同样，也不能把自己所销售的产品价格定得过低，否则，会降低自己的销售利润。

目前一些关于差异产品的定价问题的研究，陈兆波等[2]针对产品的品牌和产地存在的差异性，研究了供应链网络的均衡模型，构建了具有随机需求的多种差异产品的供应链网络均衡模型，运用随机效用理论和多项式logit模型分析了需求市场上产品的随机选择问题。罗勇等[3]研究了商品存在弹性需求的情况下，企业销售功能相同但有差异产品时的选址和定价问题，基于Hotelling模型，建立了弹性差异产品的双寡头竞争选址定价模型，利用两阶段博弈过程，得出了企业的最优选址和相应定价。Tsay等[4]研究了有一个制造商和两个独立的零售商组成的销售系统，该制造商为这两个零售商供应同一种产品。Zhao等[5]研究了由一个零售商、一个制造商组成的系统的多周期问题，在该模型中需求是确定的、价格是敏感的、依赖于时间的。

与现有研究不同，本文考虑了一个存在零售竞争的差异产品的二级供应链定价博弈问题，产品的需求依赖于存在竞争的两种差异产品的零售价格，利用博弈论方法给出了在3种不同情形下制造商和零售商的最优决策，同时分析了参数对于企业决策的影响。

1　问题描述与建模

假设系统中有一个制造商和两个竞争的零售商(分别记作零售商1、零售商2)，该制造商生产两种不同的差异产品(分别记作产品1、产品2，产品i的单位制造费用为ci,i= 1,2)，并且把这两种产品分别批发给这两个独立经营的零售商(把产品1批发给零售商1，把产品2批发给零售商2，产品i的单位批发价格为wi)，然后再由他们销售给终端顾客。假定每一种产品的市场需求都是只依赖于这两种产品的零售价格的确定性需求，产品i的需求函数定义为

Di(pi,pj)=ai-βpi+γpj

(1)

式中：i、j=1、2,i≠j，aj>0，0<β<1，0<γ<β；pi为零售商i对于产品i所给出的零售价格；ai为该种产品的市场基础，假定参数ai足够大以保证需求Di的取值总是非负的；β为每种产品的市场需求对于其自身零售价格反应程度的度量，即价格弹性；γ为每种产品的市场需求关于竞争产品价格敏感程度的度量。

假定在各参与企业之间没有任何勾结或合作，每一个系统成员都有相同的目标，即最大化自己的利润，并且他们之间的信息是对称的、完全的，制造商决策两种产品的批发价格来最大化自己的利润，两个零售商分别决策他们各自所销售产品的零售价格来最大化自身利润。即零售商i的目标是最大化自己的利润(记作πri)，πri定义为

πri=(pi-wi)Di(pi,pj)

(2)

式中：i=1，2;j=3-i；wi为制造商所给出的产品i的批发价格。

制造商的目标是最大化自己的利润(记作πm)，πm定义为

(3)

注意到每一个系统成员在系统中的地位可以影响本模型中价格博弈的求解顺序。一般来说，在一个行业中处于垄断地位的制造商所拥有的讨价还价能力要比相应的零售商所拥有的讨价还价能力强，因此在实际决策上就具有优先地位；相反，如果零售商具有较强的协商能力，则他们就可以在某种程度上降低制造商的利润，而将这部分利润转移到自身上。因此，研究探讨供应链系统中的成员的协商能力如何影响供应链系统的平衡解是非常重要的。本文分别按制造商是主导者的Stackelberg博弈、零售商是主导者的Stackelberg博弈两种情况进行讨论分析。

2　模型求解

2.1制造商是主导者的 Stackelberg 博弈

2.1.1零售商的决策

在制造商是主导者的Stackelberg博弈中，制造商首先给出他的两种产品的批发价格，零售商根据制造商所给出的两种产品的批发价格，同时决策他们将对各自所售产品所要收取的零售价格。考虑到两个零售商要同时给出决策，我们需要首先求解他们之间的Nash均衡解。

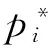
(4)

利用式(1)(2)，可以求得其一阶导数分别为

(5)

(6)

利用式(5)(6)可得二阶导数为

(7)

由式(7)看出零售商i的利润函数πri是关于决策变量pi的凹函数。因此根据上面所得到的一阶和二阶最优条件可以算出每一个零售商的最优零售价格。

令式(5)(6)等于零，并同时求解两个方程，可得在制造商是主导者的Stackelberg博弈方式下，给定制造商关于两种产品的批发价格w1、w2时，两个零售商的最优零售价格分别为

(8)

(9)

2.1.2制造商的决策

(10)

(11)

(12)

式中：M=a1-a1A+(a2-a1)E-a2B+Gc2-Hc2；N=D+F+G；Q=F-C+H；R=a2-a2A+(a1-a2)E-a1B+Gc2-Hc1。

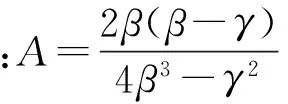
2.2零售商是主导者的Stackelberg博弈

零售商是主导者的Stackelberg博弈情形发生在零售商的地位比其制造商的地位高的情形，如沃尔玛、家乐福、苏宁电器、国美电器等大的零售商要比许多制造企业拥有更高的讨价还价能力(或者说协商能力)。在此，不失一般性，令mi表示零售商i在产品i上所获得的利润，即

pi=wi+mi

(13)

式中mi>0。

2.2.1制造商的决策

(14)

式中πm(wi,wj|p1，p2)为在给定零售商的决策结果p1、p2的条件下，且制造商给出的两种产品的批发价格分别为w1、w2时的利润。

利用式(3)可得πm关于w1，w2的一阶导数(为了书写方便，把πm(wi,wj|p1，p2)简写为πm)为

(15)

(16)

利用式(15)(16)可求得二阶导数：

(17)

通过式(17)，可以验证制造商的利润函数πm关于w1、w2的Hessian矩阵是负定的。

令式(15)(16)等于零可得两个方程，求解这两个方程可得在零售商是主导者的Stackelberg博弈方式下，分别给定两个零售商的零售价格p1、p2时,制造商的最优批发价格为

(18)

(19)

2.2.2零售商的决策

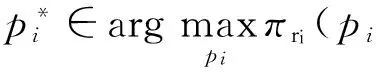
(20)

式中：i=1，2，j=3-i;πri(pi|pj，w1，w2) 为在给定零售商j的零售价格pj和制造商的批发价格w1、w2的前提下，零售商i设定产品i的价格为pi时的利润。

利用式(1)及式(18)(19)，可以得到πri关于pi的一阶、二阶最优条件(为了书写方便，把πri(pi|pj,w1，w2)简写为πri)。由二阶最优条件可知利润函数πri(pi|pj,w1，w2)是关于变量pi的凹函数。然后再对一阶最优条件进行求解可得在零售商是主导者的Stackelberg博弈方式下，零售商1和零售商2的最优零售价格为

(21)

(22)

3　参数敏感性分析

利用数值算例来比较上面两种情形所求得的理论结果，同时研究分析各参与企业在面临谈判地位变化的环境时的决策行为。通过上面不同情形下所求得的理论结果，很容易看出最优批发价、最优零售价以及需求数量都是两种产品的市场基础和生产费用的线性函数。下面分析两种情形下参数β是如何影响产品的零售价格、批发价格以及各参与方的利润。

3.1制造商主导情形下参数β的变化

从仿真结果(如图1、2所示)可以看出，在制造商为主导者的情形下，两种产品的批发价格、零售价格、市场需求量及制造商和零售商的利润都随参数β的增加而减少。

图1　批发价格、零售价格关于β的变化

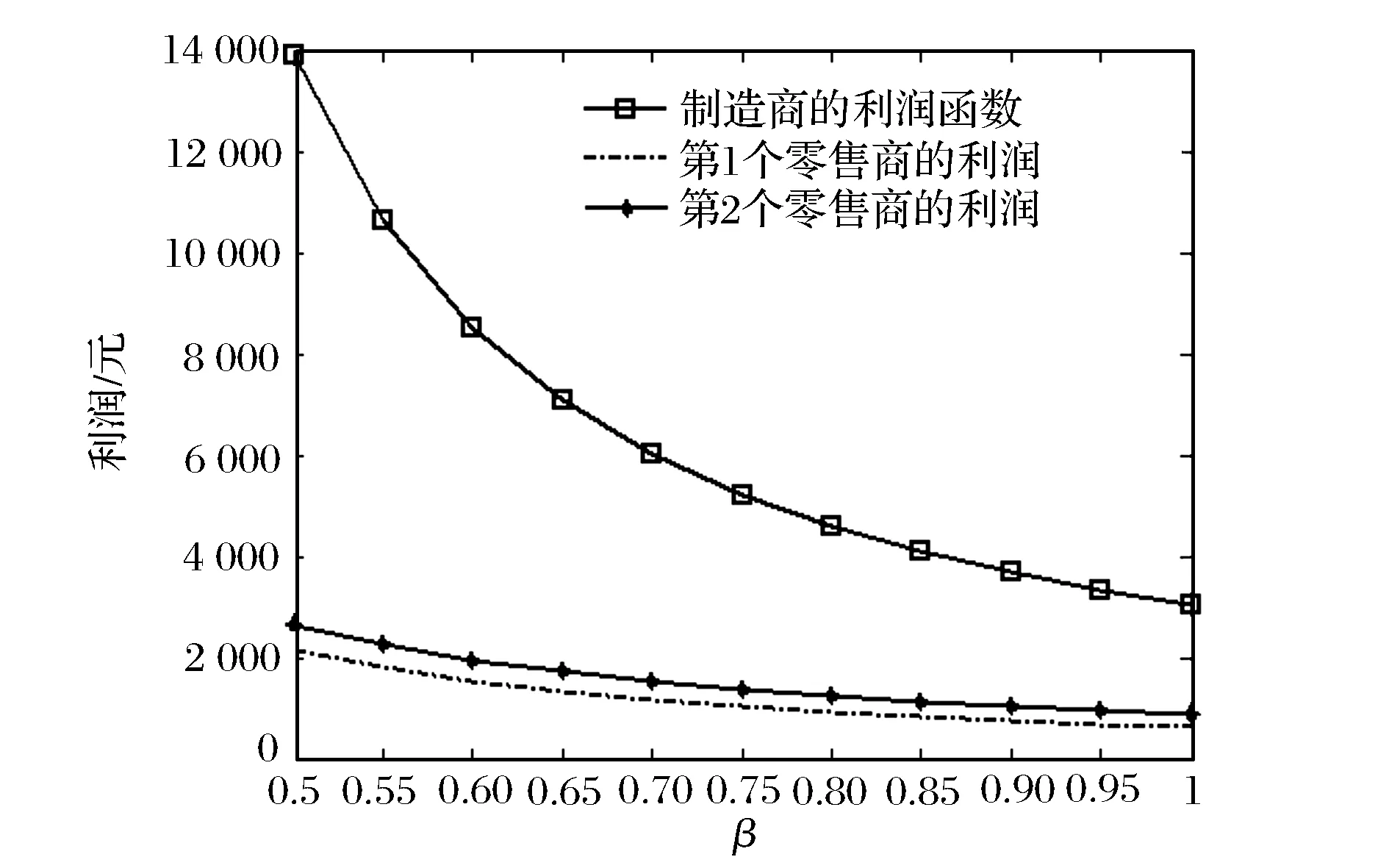
图2　利用函数关于的β变化

3.2零售商主导情形下参数β的变化

从仿真结果(如图3、4所示)可以看出，在零售商为主导者的情形下，两种产品的批发价格、零售价格、市场需求量以及制造商和零售商的利润都随参数β的增加而减少。

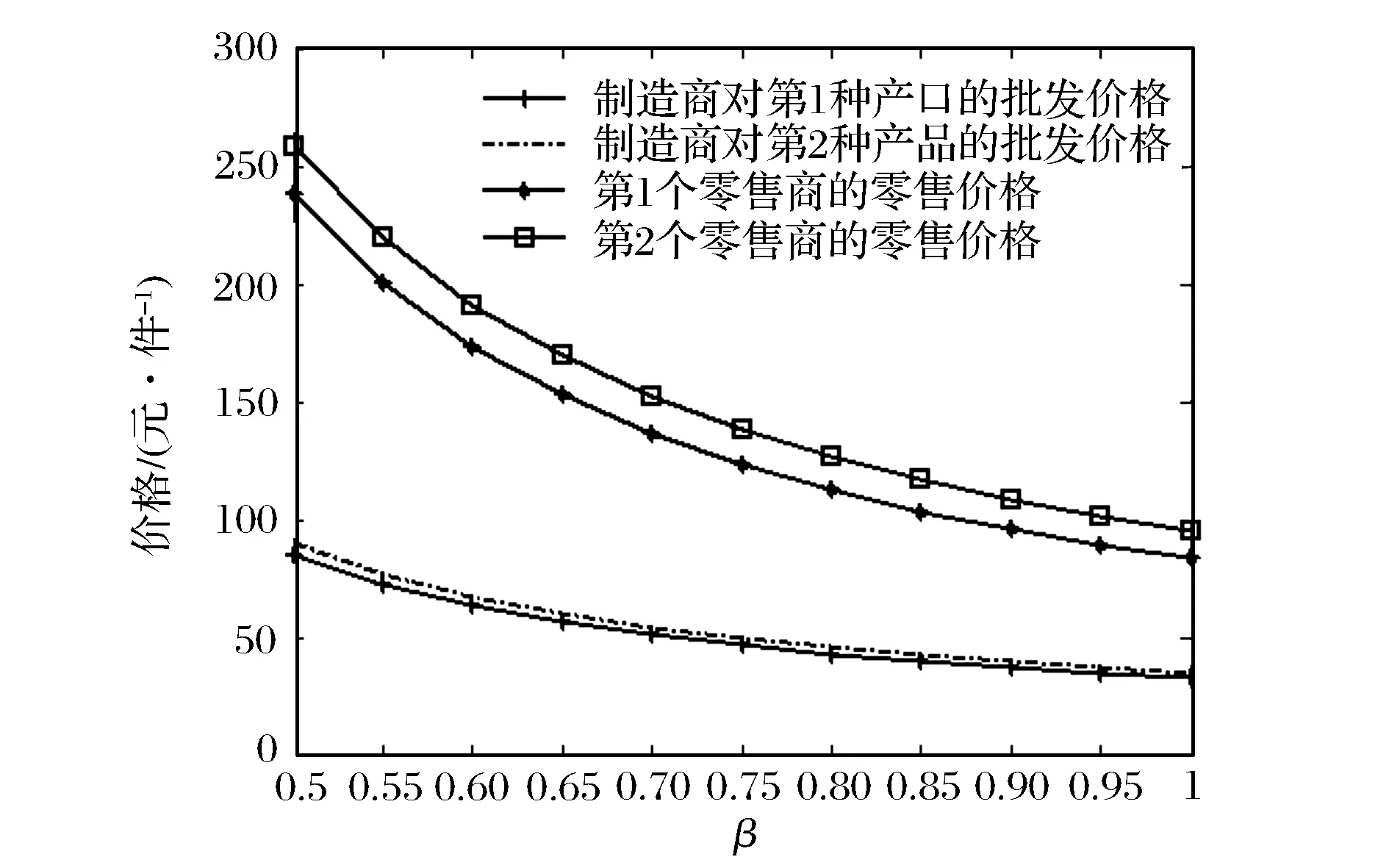
图3　批发价格、零售价格关于β的变化

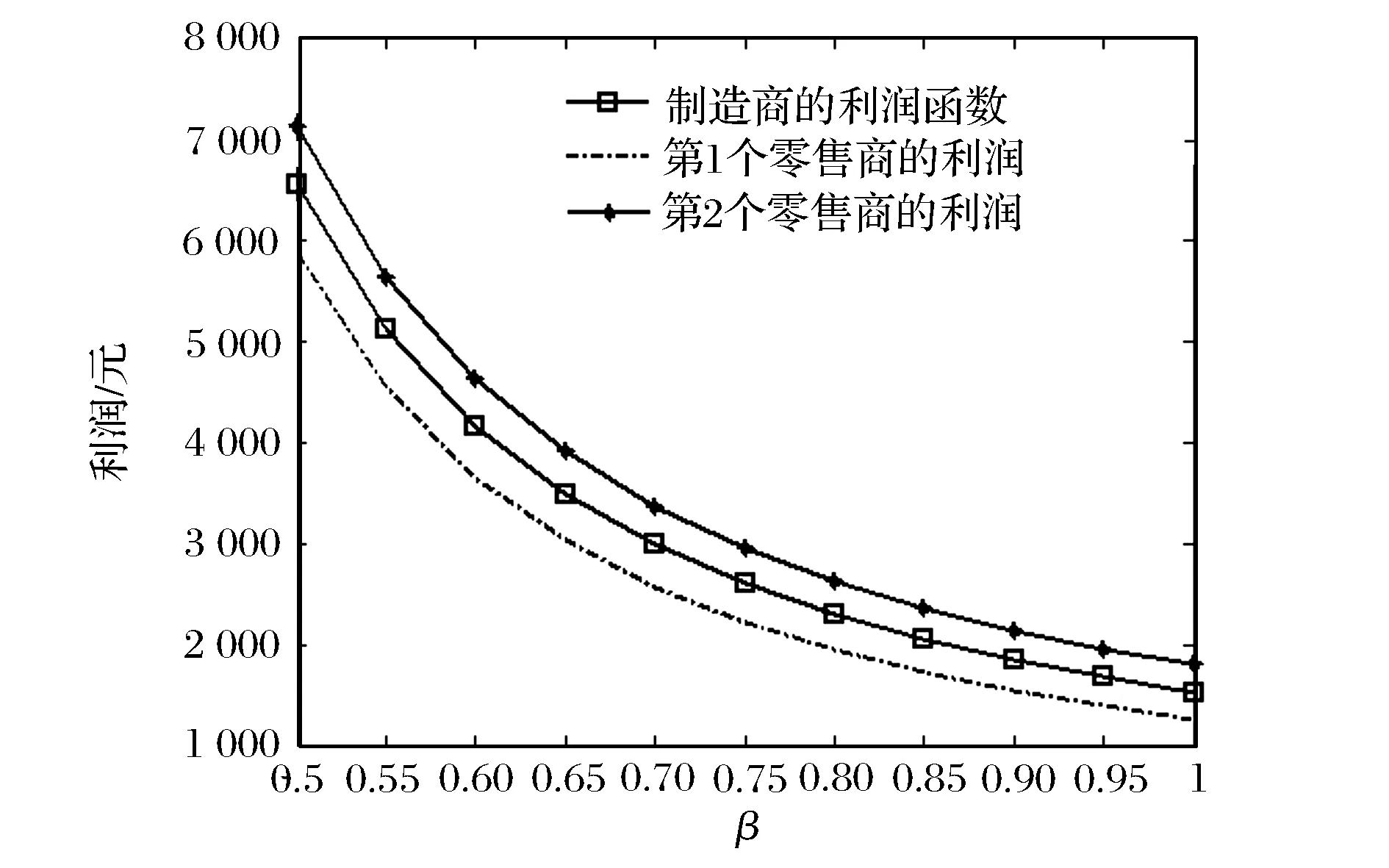
图4　利润函数关于的β变化

4　结　语

本文考虑了包含一个制造商和两个竞争零售商的二级供应链系统中的差异产品定价问题，利用博弈论方法，分别在两种不同博弈方式下给出了每一个参与企业的定价决策。另外，还对相关参数进行了数值分析，这将为企业决策提供一定的理论依据。今后可以进一步研究随机需求下企业的决策问题。

[1]HO T H, TANG C S. Research Advances in Product Variety Management[M]. Netherlands: Kluwer Publishers, 1998:25-26.

[2]陈兆波,滕春贤,姚锋敏.具有随机需求的多种差异产品供应链网络均衡模型研究[J].经济数学,2008,25(3)：271-276.

[3]罗勇,涂菶生,彭铁根,等.具有购买弹性的差异产品选址定价研究[J].南开大学学报(自然科学版),2007,40(4)：78-82.

[4]TSAY A A, AGRAWAL N. Channel dynamics under price and service competition[J].Manufacturing and Service Operations Management, 2000, 2(4)：372-391.

[5]ZHAO W, WANG Y. Coordination of joint pricing-production decisions in a supply chain[J]. IIE Transactions, 2002(34): 701-715.

(编辑：张峰)

Optimal Pricing Decisions of Two Differentiated Products

LI Meiying1, ZHAO Han2, CHEN Jing1, LI Yaling1

(1.General Courses Department, Military Transportation University, Tianjin 300161, China;2.Cadets Brigade, Military Transportation University, Tianjin 300161, China)

As to the pricing of differentiated products, suppose there is a supply chain involving one manufacturer and two retailers. This manuafcturer manufactures two differentiated products and sells them respectively to the two retailers who then sell the products to their own end customers. In this paper, by using game-theoretical approach, we examined the pricing strategy of each involved party and the different decisions they make in different situations. We also analyzed the effects of the parameters on the decisions and profits each of them make. The study is of theoretical reference value for the decision-making of an enterprise.

pricing decision； game-theory； differentiated product

2015-12-09；

2016-01-27．

国家自然科学基金资助项目(60474062, 70501014)；军事交通学院科研基金项目(2016B16).

李梅英(1981—)，女，硕士，讲师.

10．16807/j.cnki.12-1372/e.2016.05.021

C934

A

1674-2192(2016)05- 0085- 05