基于大数据处理的公共自行车服务系统研究

2016-09-20宣子岳朱家明张素洁张庆茹

赤峰学院学报·自然科学版 2016年16期

关键词：借车用车数据处理

宣子岳，朱家明，张素洁，张庆茹

（1.安徽财经大学　统计与应用数学学院；2.安徽财经大学　金融学院，安徽　蚌埠　233030）

基于大数据处理的公共自行车服务系统研究

宣子岳1，朱家明1，张素洁1，张庆茹2

（1.安徽财经大学统计与应用数学学院；2.安徽财经大学金融学院，安徽蚌埠233030）

本文针对浙江省温州市鹿城区公共自行车使用数据，使用数据透视表、GIS分析法等方法，基于公共自行车服务模式和使用规则，运用SPSS、EXCEL软件，对公共自行车服务系统从各个站点运行规律、借车人借车规律和高峰日的具体运行规律三个方面进行研究.并通过分析结果对目前公共自行车服务系统进行了评价，同时给出了提高公共自行车服务系统效率的建议.

公共自行车；大数据处理；SPSS；EXCEL

公共自行车服务系统由管理中心、站点、发卡处、调度中心、通讯网络和互联网业务平台共同组成，其中站点又包括公共自行车、锁车器和站点控制器.其运营原理是利用通讯网络信号，通过站点控制器将站点运营信息上传到管理中心服务器，管理人员利用互联网调取服务器中的站点信息，从而实现管理中心对全城各个站点的整体管控.[1]研究公共自行车的借还车规律，为公共自行车系统提供规划分析的决策支持，充分发挥公共自行车的综合优势，对改善居民的出行状况、缓解城市交通拥挤、促进城市交通可持续发展具有重要意义.

1　模型假设

⑴假设用户和借车卡之间是一一对应的关系；

⑵假设所查找到的数据真实可靠；

⑶假设用车时长在10h以上和1min以下的均为异常数据，不予以统计.

2　各站点借还车频次的统计模型

2.1研究思路

为了分别统计各站点20天中每天及累计的借车频次和还车频次,并对所有站点按累计的借车频次和还车频次分别给出它们的排序，得到每次用车时长的分布情况，借助EXCEL和SPSS对所给的数据做了处理.为了方便说明，引入了用车时长的人数分布频率的概念.

2.2数据处理

在对数据预处理的过程中，我们发现了表格中的错误，并将错误归纳如下：⑴除了180个站点外，还有编号为1000的调试点；⑵用车时长为0的数据分为两种情况，一种是因为借出自行车后，发现自行车有故障或者其他原因在一分钟之内又将其放回，另一种是由于记录中只有借车记录而没有还车记录，用车时长记为0；⑶用时在10h以上和1min以下的，均认为异常数据，不予以统计；⑷站点的编号是1~107和109~181.[1]

将20天的用车时长的数据导入SPSS后，得到了时长在0～6601分钟范围内的487组数据.我们发现用车时长集中在小于100分钟的范围内，因此对用车时长的人数分布频率进行了计算.用车时长的人数分布频率就是将用车时长按照一定的组距进行划分，划分后每组的人数除以用车总人数，结果见表1.

表1　用车时长的人数分布频率表

2.3结果分析

用EXCEL得到了各站点20天中每天及累计的借车频次和还车频次，然后对所有站点按累计的借车频次和还车频次分别进行排序，部分结果如图1、2、3、4所示.

从以上几幅图中可以直观的看出，站点的自行车借出量与归还量相差不大，也就是说借出量大的站点归还量也比较大，借出量少的站点归还量也比较少.

由图5可知，用车时长大多分布在30分钟以内，当用车时长多于30分钟时，出行者一般会考虑换乘其他交通工具继续行程.

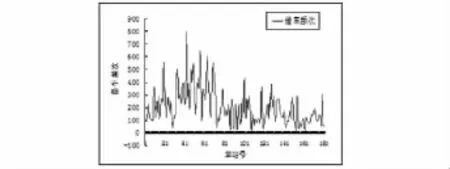
图1　第一天各站点的借车频次统计

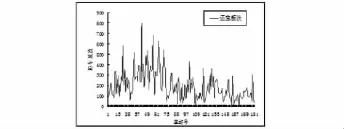
图2　第一天各站点的还车频次

图3　各站点20天累计借车频次

图4　各站点20天累计借车频次

图5　用车时长在100分钟以内的人数分布直方图

3　借车卡累计借车次数统计模型

3.1研究思路

根据温州市鹿城区借车卡办理方法规定，每张身份证限办一张借车卡，并且一张借车卡只能借一辆公共自行车.因此我们假定用户和借车卡之间是一一对应的关系，即每个用户各采用一张借车卡.为得到20天中各天使用公共自行车的不同借车卡数量，我们对数据使用EXCEL软件中的数据透视表功能对其进行处理.再利用SPSS软件的标识重复个案和选择个案功能对原始数据进行累加统计，由此得出每张借车卡累计借车次数的分布情况.

3.2数据处理

建立累加模型对每天累计借车次数以及20天总累计借车次数进行求解：

3.3结果分析

表2　不同借车卡每天累计数量

由表2可知，第20天借车人最多，第10天借车人最少.

表3　累计借车次数的区间频次统计

由表3可知，大部分人的借车次数都在30次以内，样本点99.2%的用户的借车次数都在100次以下，只有极少数人超过100次.

4　公共自行车使用次数最多一天的基本情况统计分析

4.1站点间距离的定义

4.1.1研究思路

已知站点181个，根据数理统计排列组合可知，距离数值共有C21R1组，短时间内无法通过地图精确计算任意两个站点之间的距离.因此选取不同站点间自行车代步所用的时间来估计不同站点间的距离.[3]我们定义：

s=vt

其中，v是一般自行车的骑行速度，t是不同站点之间自行车骑行的时间.

4.1.2数据处理

一般人的骑自行车速度为12~15km/h，为简便计算，取v=13.5km/h，即v=0.225km/min.[4]假设借车人从借车时起到还车时止，均在匀速骑车.部分借车站点的最近与最远还车站点及距离见表4.

表4　借车站点的最近与最远还车站点及距离（部分）

4.2借还车频次最高的站点基本情况统计分析

4.2.1研究思路

对于第二十天的数据，首先用EXCEL中的数据透视图求出所有车站的借车频次和还车频次，再对其进行排序，得到借车频次最高和还车频次最高的站点.针对所得的两个站点，对其借车时刻、还车时刻、用车时长分别进行条件筛选.由于数据量过大，为了统计方便，将时间段以两个小时为一层次、借车时长分钟段以10分钟为一段进行划分后统计出其各自分布.[6]

4.2.2数据处理

对于第二十天的数据，用EXCEL中的数据透视图求出所有车站的借车频次和还车频次，再进行排序，下表列出的是排名前十的借还车站：

表5　借车还车频次排名前十的站点统计

由上表可以知道借车频次最高的站点为42(街心公园)，还车的频次最高的站点为56(五马美食林)，对于第二十天的数据，用EXCEL中的数据透视图求出所有车站的借车频次和还车频次，再对其进行排序，得到借车频次最高和还车频次最高的站点.[5]我们将时间段以两个小时为一层次、借车时长分钟段以10分钟为一段进行划分，结果如表6、7所示.

表6　借还车时刻分布表

表7　用车时长分布

4.3各站点借还车峰值的统计分析

4.3.1研究思路

将一天中的借还车时段进行合理划分，统计出每个时间段各站点的借、还车频次，设置界定值筛选出每个车站的高峰期，并得出高峰时段各站点的借车频次和还车频次，最后对具有共同借车高峰时段和还车高峰时段的站点分别进行归类.

4.3.2数据处理

定义最小时间段为2小时，将借车还车总时间段6: 00—22:00划分为八个小的时间段.[7]统计181个站点每两个小时内的借车频次和还车频次，部分结果见表8、表9.

根据每个站点借还车频次的总和，计算每个时间段借还车频次占全天频次的比例.将两小时内借还车频次占全天比值大于0.20的时间段均称为高峰时间段.大部分站点借车高峰期和还车高峰期在8:00—10:00和16:00—18:00，相对于借车高峰期来说，还车高峰期在8:00—10:00的更多一些.这些时间正好处于上下班的高峰期，所以借还车频次增多实属正常.通过对具有共同借车高峰时段和还车高峰时段的站点的归类，可为公共自行车站点的管理提供参考，以能得到更好的管理效果，增大自行车站点的利用率.