关于2阶整数矩阵的Catalan方程*

李伟勋

(广东石油化工学院 理学院，广东 茂名525000)



关于2阶整数矩阵的Catalan方程*

李伟勋

(广东石油化工学院 理学院，广东 茂名525000)

整数矩阵；Catalan方程；特征方程；可解性

0　引言

1637年，Fermat[1-2]提出方程：

Xn+Yn=Zn，X,Y,Z∈N,n>2,gcd(X,Y,Z)=1

(1)

无解(X,Y,Z,n)。

1844年Catalan[3]提出：

Xm-Yn=1,X,Y,Z∈N

(2)

仅有解(X,Y,m,n)=(3,2,2,3)。这是两个迄今尚未完全解决的著名猜想，方程(1)和(2)分别称为Fermat方程和Catalan方程。由于这两个猜想在数论及其相关领域内有着重要的意义，人们对于它们在其他集合上的可解性进行了大量的研究[4-7]。

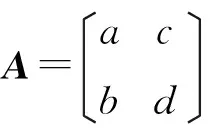
Xm-Yn=E,X,Y,Z∈S(A)，m,n∈N,m>1,n>1

(3)

的可解性。即用初等方法证明了以下结论：

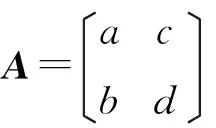
1　若干引理

设A是复数域上的n阶矩阵，En是n阶单位矩阵，则多项式fA(X)=|XEn-A|称为矩阵 A的特征多项式，代数方程fA(X)=0的根称为A的特征根。

引理1如果矩阵A的特征根都是单根，则存在n阶可逆矩阵P，可使P-1AP为如下的对角矩阵：

其中X1，…，Xn是矩阵A的全部特征根。

证明参见文献[8]的推论7.6.3。

设u，ν是正整数，此时二次方程

X2-uX-ν=0

(4)

恰有两个不同的实根：

(5)

引理2如果正整数α，β适合α>β，则必有：

(6)

证明由于α-β≥1，从(5)可知X1>1，故有：

故(6)成立。

2　定理证明

设(X,Y,m,n)是方程(3)的一个解，根据集合S(A)的定义，可知存在正整数r,s，可使X=Ar以及Y=As，代入(3)立得：

Arm-Asm=E

(7)

假如rm=sn，则(7)的左边等于O，故不可能，因此rm≠sn。

设u=a+b,ν=bc-ad,矩阵A的特征多项式

fA(X)=|XE-A|=X2-uX-ν

(8)

因此(8)恰有两个适合(5)的不同特征根X1和X2，于是根据引理1可知，存在2阶可逆矩阵P，使得：

(9)

因为对于任何正整数t，有P-1AtP=(P-1AP)t，所以从(7)和(9)可得：

P-1(Arm-Asn)P=P-1ArmP-P-1AsnP=(P-1AP)rm-(P-1AP)sn=

(10)

从(10)可得：

(11)

由于rm≠sn，而且X1>1，所以当rmsn时,由于n>1，所以sn>1，由引理2可知此时(11)也不成立。综上所述，方程(3)无解(X,Y,m,n)。

[1] Ribenboim P. 13 lectures on Fermat's last theorem[M]. New York: Springer Verlag，1979.

[2] Frejman D. On Fermat's equation in the set of Fibonacci matrices [J]. Discussiones Mathematicae，1993，13(1):61-64.

[3] Catalan R. Note extraite d'une letter addressee editeur[J]. J.Reine Anew Math，1844(27):192-193.

[4] LIU Zhiwei. The generalized Catalan conjecture[J]. Journal of Math,2013(3):1107-1114.

[5] Frejman D. On Fermat’s equation in the set of Fibonacci matrices[J]. Discuss. Math,1993(13):61-64.

[6] Grytczuk A. On Fermat’s eqution in the set of integral 2×2 matrices[J]. Period. Math. Hunger,1995(30):79-84.

[7] Q.Li, M-H. Le. A note on Fermat’s eqution in 2×2 matrices[J]. Discuss. Math,1995(15):135-136.

[8] 张禾瑞,郝炳新.高等代数[M].北京:高等教育出版,1984.

(责任编辑：柳丰)

On the Catalan’s Equation in 2×2 Matrices

LI Weixun

(College of Science ，Guangdong University of Petrochemical Technology ，Maoming 525000，China)

Let A=be a nonsingular integral 2×2 matrices，anda+b>0 withbc>ad, proved that the Catalan's equation in 2×2 matrices has no solution, by using some properties of eigenvalues of matrices.

Integer matrix; Catalan's equation; Characteristic equation; Solvability

2016-05-22；

2016-07-18

李伟勋(1971—)，男，广东茂名人，副教授，研究方向为初等数论。

O156.7

A

2095-2562(2016)04-0059-02