基于动水及桩-土-结构相互作用的斜拉桥地震响应分析

高大峰， 路　军， 董　旭， 陈凯旋

(西安建筑科技大学 土木工程学院， 陕西 西安　710055)



基于动水及桩-土-结构相互作用的斜拉桥地震响应分析

高大峰， 路军， 董旭， 陈凯旋

(西安建筑科技大学 土木工程学院， 陕西 西安710055)

为了得到更为符合实际情况的跨江大桥动力稳定性的地震反应分析，在桥梁抗震研究中必须综合考虑动水及桩-土-结构的相互作用。基于此，结合某斜拉桥，采用基于Morison方程的动水力简便计算方法来模拟水对桥梁下部结构的动水压力，通过大型有限元程序Midas/Civil分别建立了没有考虑动水及桩土效应和考虑动水及桩土效应两种情形下的计算模型，通过输入El-Centro波分析了动水及桩土效应对斜拉桥结构动力特性和地震反应的影响。分析表明动水及桩土效应对斜拉桥动力特性和地震反应的影响较大，因此在对跨江斜拉桥结构进行抗震分析时，应考虑动水及桩土效应对其动力反应的影响。

斜拉桥； 动水及桩-土-结构的相互作用； 抗震分析； 动水压力

0　前言

近年来，随着交通运输事业的不断发展，我国出现了许多在建和拟建的跨江跨海桥梁，其中许多桥梁处于深水之中[1]，即部分桥墩和基础位于深水中。在地震作用下，桥梁下部结构的运动会使得下部结构周围的水体产生辐射波浪运动，且由于下部结构与水体之间的相对运动，水体会在桥梁的下部结构作用有动水压力，该动水压力对结构的动力特性和动力响应有很大的影响。故充分认识地震作用下动水与桩土效应对斜拉桥结构的影响，对于深水斜拉桥的抗震设计和安全评估有非常重要的意义。

国内外学者对动水及桩土效应对跨江桥梁的地震响应进行了一定的研究。Liaw和Chopra[2]依据辐射波浪理论得到了柔性圆截面柱体的动水压力解析解，并且分析了附加质量法和水体压缩性等对柱体结构自振特性的影响；Goyal和Chopra[3]在考虑土与结构相互作用的基础上进一步研究了具有两个对称轴的任意截面形状柱体的动水压力；李玉成等[4]通过分析波浪对海上建筑物的影响，得出建筑物与流体之间的相互作用会对结构自身的动力反应产生很大的影响；郑海容等[5，6]在考虑作用在桥墩上的动水压力的情况下，进行了桩土-桥墩-流体相互作用体系的地震反应分析；李彤[7]采用Morison方程考虑了地震动水压力，对土一群桩一结构一水相互作用体系进行了地震响应分析。基于以上理论，本文对某斜拉桥结构在考虑动水及桩-土作用的情况下进行地震反应分析[8，9，11]。

1　计算方法

1.1地震激励下动水与桥梁结构的相互作用分析

根据Morison动水理论，假定水体是理想、不可压缩的，且忽略结构的运动对水体运动产生的影响，认为水体对结构的作用是由动水惯性力(加速度场引起的)和动水阻力(速度场引起的)两部分组成，则水体对柱体结构的动水压力计算表达式为[13]：

(1)

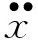
因为忽略了结构对水体运动的影响，于是水体质点的速度和加速度均为零，则式(1)可改写为：

(2)

由于式(2)右端的第二项是非线性项，在具体的计算过程中比较困难，因此采用文献[7]拟线性化的方法，则第二项可表示为：

(3)

式(3)中：xms为速度的均方根值。因此经过线性化处理得到新的线性Morison方程如下所示：

(4)

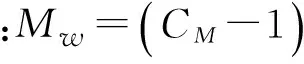
假设柱体结构中在相邻单元中点之间的部分水与结构的相对速度是一致的，并且作用在柱体结构第i个节点上的作用力等于与i点相连的各柱体构件受力总和的一半，则可以得到柱体结构的节点i处的动水等效附加质量如下所示：

(5)

式中：j为与柱体结构的节点i相邻单元的节点；lij为柱体结构第ij单元的有效长度的一半。

故高桩承台桥梁结构在地震激励下的运动方程可表示为如下形式：

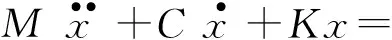
(6)

1.2桩-土-结构动力相互作用分析

对于处在深软地基中的桥梁结构，其桩-土-结构之间的动力相互作用问题一直是学术界非常棘手且热门的话题。我国目前在建或已建的桥梁，在选址上大多跨越了江河湖泊，而江河湖泊所处的深软场地对于桥梁结构的抗震来说是个非常不利的因素。在地震作用过程中，桥梁上部结构产生的惯性力通过基础反馈给地基，导致地基产生变形，地基的变形又反过来引起桥梁上部结构产生移动或摆动，从而导致上部结构的实际运动与按刚性地基假定计算的结果间出现较大的差异，这便是由地基与结构之间的动力相互作用引起的[10]。

在求解群桩基础的等代动力刚度时，由于桩周土对桩基础的弹性支承作用，此时可以把桩基础视为一种受到弹性支承的地基梁。在桩顶弯矩及横向荷载的作用下，计算桩基础的内力和位移的方法主要有四种：弹性理论法、弹性地基反力法、极限地基反力法以及复合地基反力法。弹性地基反力法又可以分为线弹性地基反力法和非线弹性地基反力法。由于Winkler假定中地基系数的不同取值，线弹性地基反力法中又派生出了m法、K法、C法以及张有龄法。由于m法简单实用，故国内的地基基础设计规范大都推荐采用该方法，m法的基本公如下式(9)和式(10)所示：

σy=Cy·x

(9)

Cy=my

(10)

式(9)和(10)中：σy为土层的横向水平抗力，MPa；Cy为土层深度y处的水平地基系数，MPa/m；m为水平地基系数随土层深度变化的比例系数，MPa/m2；x为土的横向位移，m；y为土层自地面或局部冲刷线往下的深度，m。

当采用m法计算桩基础周围的土体刚度时，首要的是确定m值。m法中所需土层的m值以实测数据为依据，根据公式(9)、式(10)得到：

m=σy/(x·y)

(11)

当土体的比例系数不能通过试验得到时，可以通过查阅文献[14]得到。在计算群桩基础的等效动力刚度时，m值应取为规范所提供的静力值的2倍～3倍。

根据式(11)可以求得每层土的等代弹簧刚度ks如下式所示：

ks=abpmy

(12)

式中：a为土层的厚度；bp为桩柱所在的土层宽度，一般取桩柱的计算宽度，这里取bp=0.9(D+1)，D是桩柱的直径。

2　工程概况

某斜拉桥的跨径布置为17×40 m+120 m+270 m+120 m+16×40 m，主桥采用120 m+270 m+120 m的斜拉桥，引桥采用40 m装配式部分预应力混凝土组合箱梁(先简支后结构连续)。该斜拉桥主桥的桥型为双塔双索面混凝土边主梁斜拉桥，孔跨布置为41.6 m+78.4 m+270 m+78.4 m+41.6 m，边跨设有辅助墩。主梁为双向预应力混凝土结构，支承体系采用半漂浮体系，在边墩、辅助墩墩顶处设纵向活动支座，单侧横向约束；在主塔处设纵向活动支座及阻尼器，横桥向设有横向支座。主塔是由上塔柱(斜拉索锚固区)、中塔柱、下塔柱及横梁组成的框架结构，为偏心受压受力构件。主要技术标准为：双向6车道高速公路，主桥两侧各设1.5 m宽人行道；公路I级设计荷载；计算行车速度100 km/h；地震动峰值加速度0.05 g；通航净空高度为21 m，通航净宽91 m，设计最高通航水位6.4 m。

采用Midas/Civil软件建立该斜拉桥动力计算的三维有限元模型(见图1)，在模型中主梁、主塔、承台以及桩基等均采用三维梁单元模拟，斜拉索采用桁架单元模拟。该斜拉桥主桥支承体系采用半漂浮体系，在边墩、辅助墩墩顶处设纵向活动支座，单侧横向约束；在主塔处设纵向活动支座及阻尼器，横桥向设有横向支座，用主梁与墩项结点自由度之间的弹性连接来模拟支座单元的作用。

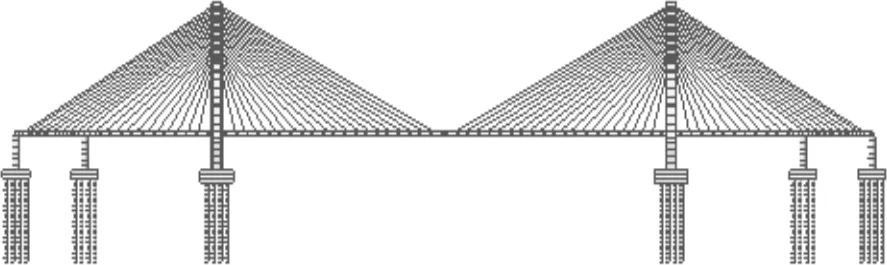
图1　斜拉桥三维有限元模型Figure 1　　　　Three-dimensional finite element model of cable-stayed bridge

3　动水及桩-土-结构相互作用对斜拉桥

动力特性的影响

自振特性分析是研究桥梁结构动力反应的基础，它决定了桥梁结构的动力反应特征，故在进行地震反应分析之前首先对该斜拉桥有无桩土水两种模型进行自振特性分析。并得出相应的结构动力特性，表1中列出了有无桩土水两种模型下结构的前8阶频率和振型特征，并求出了结构在有桩土水状态下的自振频率fy与无桩土水状态下的自振频率fw的比值fy/fw。

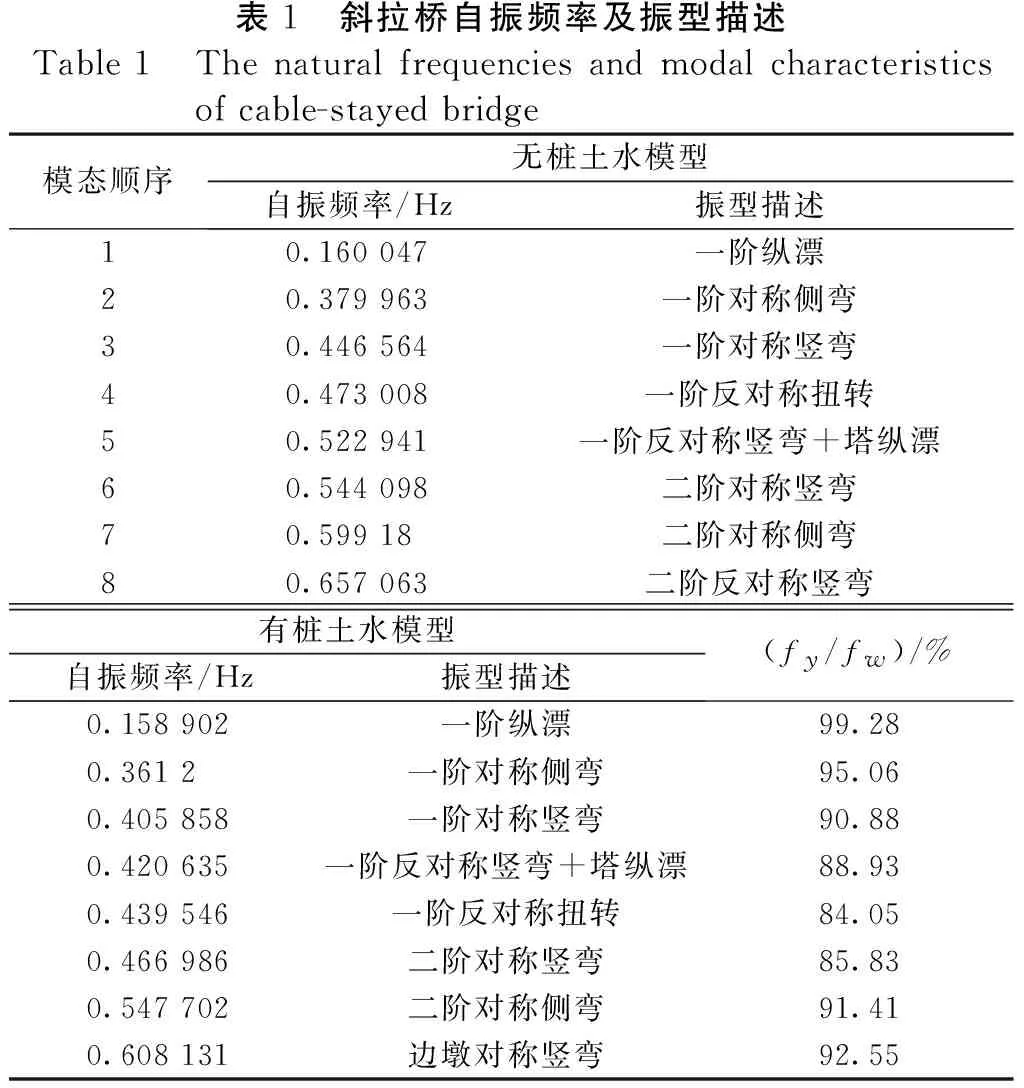
表1 斜拉桥自振频率及振型描述Table1 Thenaturalfrequenciesandmodalcharacteristicsofcable-stayedbridge模态顺序无桩土水模型自振频率/Hz振型描述10.160047一阶纵漂20.379963一阶对称侧弯30.446564一阶对称竖弯40.473008一阶反对称扭转50.522941一阶反对称竖弯+塔纵漂60.544098二阶对称竖弯70.59918二阶对称侧弯80.657063二阶反对称竖弯有桩土水模型自振频率/Hz振型描述(fy/fw)/%0.158902一阶纵漂99.280.3612一阶对称侧弯95.060.405858一阶对称竖弯90.880.420635一阶反对称竖弯+塔纵漂88.930.439546一阶反对称扭转84.050.466986二阶对称竖弯85.830.547702二阶对称侧弯91.410.608131边墩对称竖弯92.55

对于斜拉桥结构体系，纵漂振型对结构的纵向地震反应的影响较大，对于漂浮或半漂浮体系，纵漂振型通常是最低阶的振型。该斜拉桥结构的第一阶振型是纵漂，结构的第一阶自振周期是6.25 s，属于长周期结构。另外，从表1可以看出：在该斜拉桥结构的前8阶振型中，水及桩土效应对结构的自振特性有一定的影响，由于结构上的动水附加质量和桩-土效应的影响，使得该斜拉桥结构的自振频率有所降低。在该斜拉桥结构的前8阶振型中自振频率的降低幅度最大约达16%(第五阶振型)，所以在计算中必须考虑附加水质量和桩-土-结构相互作用对全桥自振频率的影响。由于动水和桩土效应的影响，一些振型的出现次序发生了改变，与不考虑桩土水时相比，有桩土水时的第5阶和第9阶振型分别变成了第4阶和第8阶振型。

4　地震激励下动水及桩-土-结构相互作

用对斜拉桥动力响应的影响

4.1动水及桩-土-结构相互作用对斜拉桥位移反应的影响

该斜拉桥桥址的基本烈度为6度，地震动峰值加速度为0.05 g，根据《公路桥梁抗震设计细则》(JTG/T B02-01-2008)[15]中的规定按照7度抗震设防烈度进行结构的抗震设计验算，则水平向的设计地震动加速度峰值是0.1 g。地震反应计算中采用了El Centro地震波的南北分量，计算中地震波峰值调整为0.1 g。采用瑞利(Rayleigh)阻尼，阻尼系数取0.05。

在前述建立的有限元计算模型的基础上，采用两种工况对该斜拉桥的进行了地震反应分析。工况1：不考虑动水与桩-土效应；工况2：考虑动水与桩-土效应。图2和图3分别给出了2种工况下主梁跨中和左塔塔顶的纵桥向位移时程曲线。

从图中可以看出：当考虑动水及桩土相互作用时，跨中纵桥向位移在t=36.02 s时位移达到了负向最大值，最大值为-0.135 m，t=39.18 s时达到了正向最大值，最大值为0.138 m。塔顶纵桥向位移在t=36.04 s时位移达到了负向最大值，最大值为-0.14 m，t=39.16 s时达到了正向最大值，最大值为0.145 m。当不考虑动水及桩土相互作用时，跨中纵桥向位移在t=35.36 s时位移达到了负向最大值，最大值为-0.107 m，t=32.4 s时达到了正向最大值，最大值为0.105 m。塔顶纵桥向位移在t=35.38 s时位移达到了负向最大值，最大值为-0.113 m，t=32.3 s时达到了正向最大值，最大值为0.112 m。由于动水及桩土效应的影响，主梁跨中和塔顶的纵桥向位移在两种工况下有显著的差别，考虑桩土水时的主梁跨中和塔顶纵桥向位移峰值比不考虑桩土水时出现的时间滞后，且其纵桥向位移的最大峰值普遍高于无桩土水时的最大峰值。通过比较2种工况下主梁跨中和塔顶的纵桥向位移可知，无论是塔顶还是主梁跨中，其地震响应都有不同程度的增加，在主梁跨中处达到了31.31%，在塔顶达到了23.57%，因此在对跨江深水斜拉桥进行地震响应分析时，应考虑动水及桩土相互作用对斜拉桥结构的影响。

图2　跨中纵桥向位移Figure 2　Across the elevated to displacement

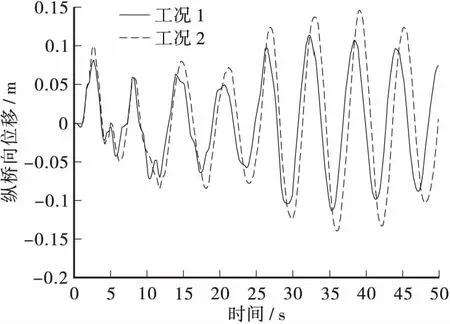
图3　塔顶纵桥向位移Figure 3　Elevated tower top displacement

4.2动水及桩-土-结构相互作用对斜拉桥内力反应的影响

为了分析地震作用下动水及桩-土-结构相互作用对斜拉桥结构的内力的影响，采用影响系数R来表示动水及桩-土效应对结构地震响应的最大值的影响。

表2给出了工况1、2 情况下左塔塔底的内力计算结果，图4～图6分别给出了工况1，2 情况下左侧辅助墩及边墩的内力变化曲线。

通过对表2和图4～图6的计算数据进行对比分析可知：动水和桩-土-结构相互作用对斜拉桥塔墩的内力影响很明显，具体分析如下：

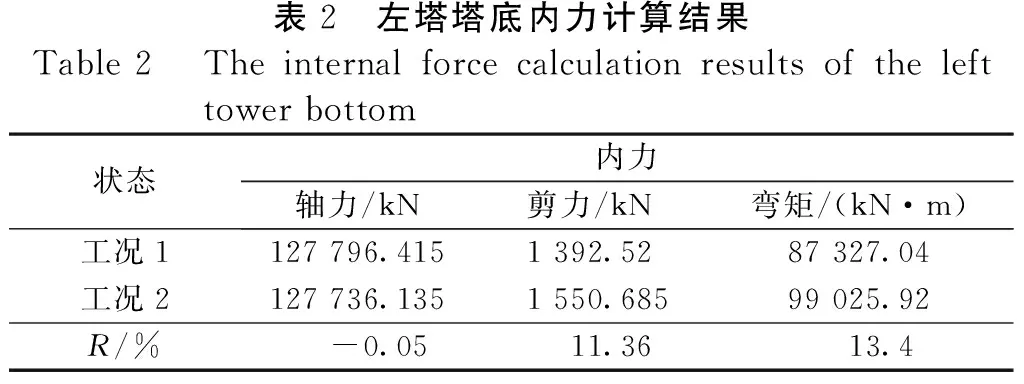
表2 左塔塔底内力计算结果Table2 Theinternalforcecalculationresultsofthelefttowerbottom状态内力轴力/kN剪力/kN弯矩/(kN·m)工况1127796.4151392.5287327.04工况2127736.1351550.68599025.92R/%-0.0511.3613.4

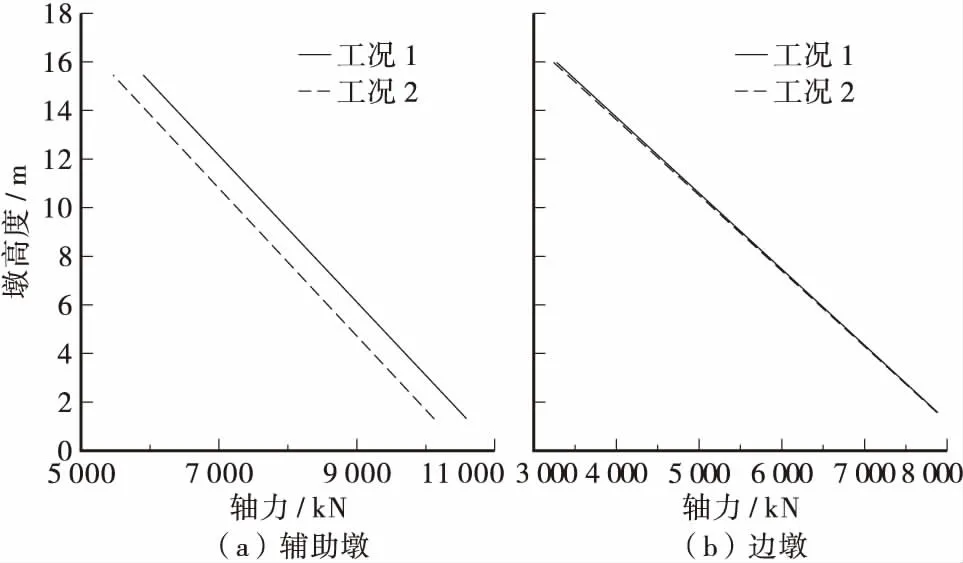
图4　左侧辅助墩及边墩轴力变化曲线Figure 4　　　　The axial force change curves of the left auxiliary pier and side piers

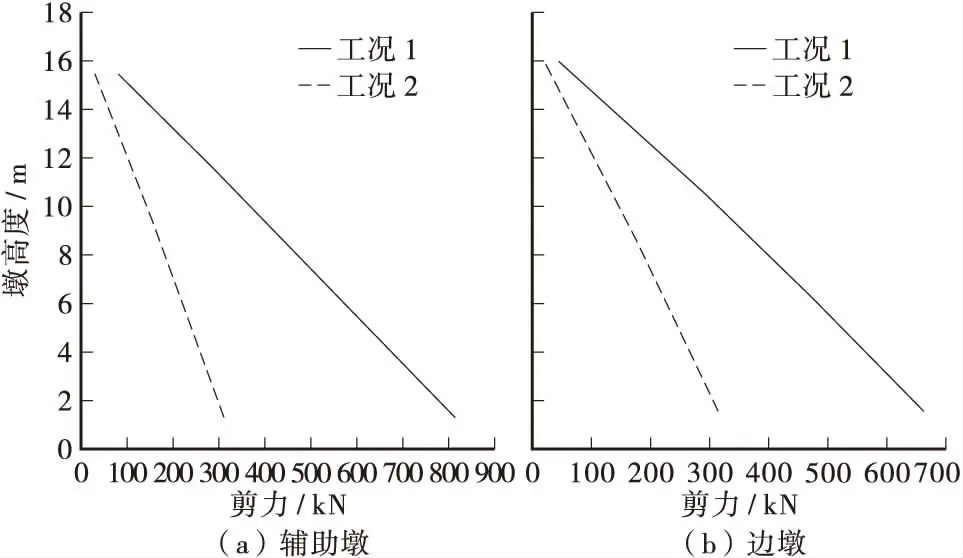
图5　左侧辅助墩及边墩剪力变化曲线Figure 5　　　　The shear change curves of the left auxiliary pier and side piers

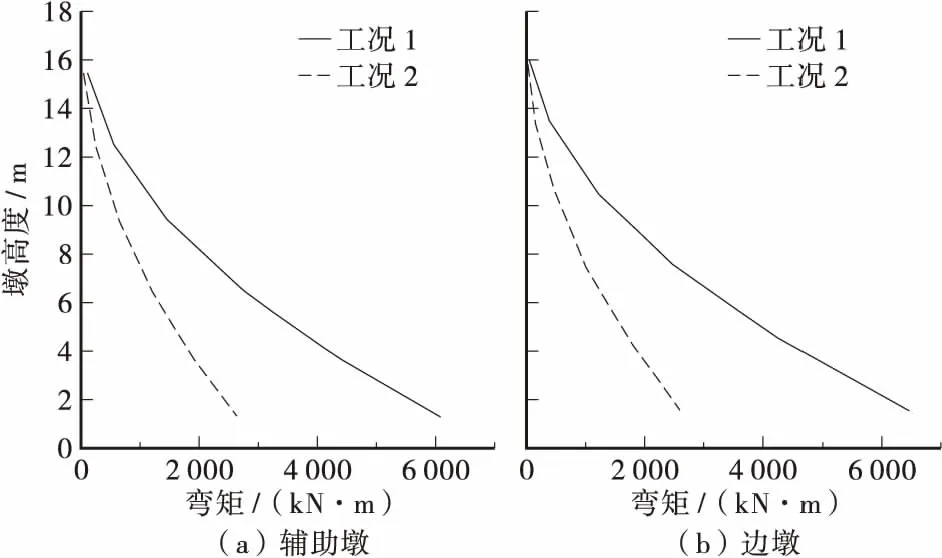
图6　左侧辅助墩及边墩弯矩变化曲线Figure 6　　　　The bending moment change curves of the left auxiliary pier and side piers

将工况2与工况1中的计算结果进行对比可知：工况2中左塔塔底最大轴力比工况1减少了0.05%，而辅助墩和边墩墩底最大轴力比工况1分别减少了4.5%和0.15%；工况2中左塔塔底最大剪力比工况1增加了11.36%，而辅助墩和边墩墩底的最大剪力比工况1的分别减少了61.62%和52.45%；工况2中左塔塔底的最大弯矩比工况1增大了13.4%，而辅助墩和边墩墩底最大弯矩比工况1 分别减少了56.56%和59.6%。

从以上分析可知：当对深水斜拉桥进行地震反应分析时，考虑动水及桩土效应与否，对斜拉桥结构塔墩轴力的影响较小，而对塔墩剪力和弯矩的影响较大，由此可见，对于跨江斜拉桥，抗震计算中有必要考虑动水压力及桩土效应的影响，忽略动水压力及桩土效应可能低估其动力反应。

5　结论

本文采用基于Morison方程的动水力简便计算方法，以某斜拉桥为例进行了有无桩土水时的地震动力响应分析，其中重点研究了动水及桩-土-结构相互作用对该斜拉桥自振特性的影响，对比了无桩土水和有桩土水两种状态下斜拉桥结构的自振频率及各阶振型变化。此外，还分析了动水及桩-土-结构相互作用对斜拉桥结构的动力反应影响，讨论了动水及桩-土-结构相互作用对斜拉桥主梁、主塔及塔墩内力的影响情况。主要结论包括：

① 该斜拉桥结构的第一阶振型是纵漂，结构的一阶自振周期是6.25 s，属于长周期结构。动水及桩土结构相互作用使得该斜拉桥各阶频率都有不同程度的减小，在该斜拉桥结构的前8阶振型中自振频率的降低幅度最大约达16%(第五阶振型)，一些振型的出现次序也发生了变化，故在计算中必须动水和桩-土效应对全桥自振频率的影响。

② 在地震波激励下，考虑动水压力及桩土相互作用时，斜拉桥塔顶和跨中主梁的纵桥向位移都有不同程度的增加，在主梁跨中处增幅达31.31%，在塔顶处增幅达23.57%。另外，考虑动水及桩土作用时塔顶和跨中的纵桥向最大位移出现的时间延迟。

③ 对深水斜拉桥进行地震反应分析时，考虑动水及桩土效应与否，对斜拉桥结构的塔墩轴力影响较小，而对塔墩剪力和弯矩的影响较大，如果忽略动水及桩土效应的影响可能会低估其动力反应。同

时，由于桥梁结构体系的差异和地震动的随机性，这种动水及桩土的作用还应进一步的深入研究，以使深水斜拉桥结构的地震反应分析更加合理。

[1]项海帆.21世纪世界桥梁工程的展望[J].土木工程学报，2000，33(3)：126.

[2]Liaw C Y，Chopra A K.Dynamics of towers surrounded by water[J].J.Earthquake Engineering and Structural Dynamics，1974，18(3)：32-33.

[3]Goyal A，Chopra A K.Earthquake analysis of intake outlet towers including tower water foundation soil interaction[J].Earthquake Engineering and Structural Dynamics，1989，18(3)：325-344.

[4]李玉成，滕斌.波浪对海上建筑物的作用[M].北京：海洋出版社，1993.

[5]郑海容.桩-土-上部结构-流体相互作用体系的地震反应分析[J].桥梁建设，1992(4)：67-75.

[6]吴明军，陈文元，肖盛莲.地震和波浪力共同作用下桥墩的动力响应研究[J].四川建筑科学研究，2010，36(6)：21-25.

[7]李彤.地震作用下土-群桩-结构-水相互作用体系的动力反应分析[D].上海：同济大学，1999.

[8]房营光，孙钧.平台-群桩-水流-土体系统的地震反应分析[J].土木工程学报，1998，31(5)：56-64.

[9]范立础，叶爱君.大跨度桥梁抗震设计[M].北京：人民交通出版社，2001.

[10]李国豪.桥梁结构稳定与振动[M].北京：中国铁道出版社，1996.

[11]屈爱平，高淑英.梁-墩-桩基的动力特性研究[J].西南交通大学学报，2001，36(6)：641-644.

[12]袁迎春，赖伟，王君杰.Morison方程中动水阻尼项对桥梁桩柱地震反应的影响[J].世界地震工程，2005，21(4)：88-94.

[13]宋波，李悦.高桩承台动水力简便计算方法[J].北京科技大学学报，2011，33(4)：509-514.

[14]JTJ D63-2007，公路桥涵地基与基础设计规范[S].

[15]JTG/T B02-01-2008，公路桥梁抗震设计细则[S].

Seismic Response Analysis of Hydrodynamic and Pile-soil-structure Interaction for Cable-stayed Bridge

GAO Dafeng， LU Jun， DONG Xu， CHEN Kaixuan

(School of Civil Engineering， Xi’an University of Architecture and Technology， Xi’an， Shanxi 710055， China)

In order to achieve the better response analysis of river-spanning bridge，the dynamic water and pile-soil-structure interaction are considered.Based on a cable-stayed bridge，use the dynamic hydraulic simple calculation method based on the Morison equation to simulate the dynamic water pressure on the lower part of the bridge structure，through the finite element program MIDAS/Civil respectively established without the dynamic water and pile-soil-structure interaction and considering the dynamic water and pile-soil-structure interaction the two calculation model of the bridge，through input El centro seismic wave to analysis the dynamic characteristics and seismic response of cable-stayed bridge under the dynamic water and pile-soil-structure interaction.Analysis shows that the dynamic water and the effect of piles and soil influence on the dynamic characteristics and seismic response of cable-stayed bridge is bigger，so when analysis the seismic of cable-stayed bridge across the river，the effect on its dynamic response by the dynamic water and pile-soil-structure interaction should be considered.

cable-stayed bridge； the dynamic water and pile-soil-structure interaction； seismic analysis； dynamic water pressure

2015 — 03 — 23

国家自然基金项目(51408453)；陕西省重点学科建设专项资金资助项目(E01004)

高大峰(1962 — )，男，河北乐亭人，教授，从事建筑结构与抗震方面的教学与科研工作。

U 448.27

A

1674 — 0610(2016)04 — 0019 — 05