基于微动参数估计的非对称进动目标三维成像
2016-09-20胡晓伟童宁宁何兴宇王宇晨空军工程大学防空反导学院陕西西安710051
胡晓伟,童宁宁,何兴宇,江 东,王宇晨(空军工程大学防空反导学院,陕西 西安710051)
基于微动参数估计的非对称进动目标三维成像
胡晓伟,童宁宁,何兴宇,江 东,王宇晨
(空军工程大学防空反导学院,陕西西安710051)
具有非对称结构的进动目标成像是目前空间目标成像的一个难点。在构建非对称进动目标回波模型的基础上,分析了成像所需的4个微动参数并给出了相应的参数估计方法。在微动参数已知的前提下,提出了一种基于三维复数逆投影变换的进动目标三维成像的方法。首先利用微动参数构建相位补偿因子,之后对时间距离像进行三维搜索,进而实现进动目标的三维成像。最后通过仿真实验验证了所提方法的有效性,同时仿真分析了微动参数估计误差对成像的影响。
非对称进动目标;微动参数估计;三维复数逆投影;三维成像
网址:www.sys-ele.com
0 引 言
空间进动目标成像对于弹道目标识别[1]、空间碎片监测等都具有重要意义。然而由于进动目标运动形式的复杂性,使得对进动目标的成像十分困难。目前,对于空间进动目标成像的研究主要集中在旋转对称目标。对于旋转对称目标,其回波不受自旋运动调制,目标上非理想散射中心[2-3]的运动可近似为正弦变化[4],因此可将目标的进动等效为各个散射点的自旋,进而利用自旋目标成像方法进行成像。文献[5]针对高速自旋目标,提出了相干单距离多普勒干涉高分辨二维成像方法;文献[6]基于窄带雷达信号,提出一种基于时频分析和广义Radon变换的空间进动锥体目_标_的_二_维重构算法;文献[7]在分析弹道目标进动效应基础上,利用时频分析实现了旋转对称目标的成像;文献[4]研究了一种锥形进动目标的微动估计方法和高分辨三维成像方法。然而对于进动的非对称目标,目标上的尾翼等非对称结构作锥旋和自旋的复合运动,运动形式复杂,以上针对自旋目标的成像方法此时将不再适用。对于非对称目标,文献[8]利用复数经验模式分解实现了目标主体回波和非对称结构回波的分离,并对分离后的主体回波进行了成像。但这种方法不能实现非对称结构的成像,且只能获取目标二维像,损失了目标信息。文献[9]通过提取目标的微动特征,实现了非对称自旋目标的三维成像,但该方法只适用于微动形式为自旋的目标。而对于非对称进动目标的三维成像,目前还未见到相关研究成果。
进动目标成像的复杂性源于其微动形式的复杂性。目前多数基于逆合成孔径雷达(inverse synthetic aperture radar,ISAR)成像方法的前提都是目标作微转动,当目标微动形式不满足微转动时,成像方法将不再适用。但如果能够提前获知目标的微动特性[10-11],便有望实现对复杂微动目标的成像。目前关于目标微动特性的研究已取得了许多成果。文献[12]研究了利用微多普勒分析提取弹道目标微动特征;文献[13]提出了一种有翼弹头进动特征提取方法;文献[14]在分布式组网雷达下实现了进动目标锥旋矢量、进动周期和自旋周期等进动特征的提取;文献[15]提出了一种基于雷达高分辨距离像求解进动锥体目标微动参数与几何外形参数的方法。以上关于目标微动特征提取的研究为复杂微动目标的成像提供了可能。本文通过建立非对称进动目标模型,分析了反映目标进动特性的微动参数,并给出了微动参数的估计方法,在此基础上利用三维逆投影变换的方法实现了非对称进动目标的三维成像。
1 非对称进动目标回波模型
理论和实验表明,目标在高频区的雷达回波可近似等效为多个强散射点回波的合成[2]。对如图1所示的含尾翼锥体目标,其等效强散射中心包括锥顶散射点P0和4个对称分布的尾翼散射点P1,P2,P3,P4。锥体在绕目标对称轴y轴作自旋的同时,绕进动轴Y轴作锥旋运动。其中XYZ为参考坐标系,xyz为目标本地坐标系,雷达视线方向(line of fight,L O S)为L O S。

图1 非对称锥体进动模型
对于锥体上任一散射点P,设其在本地坐标系中的初始位置为rP,则t时刻P在参考坐标系中的位置可表示为

式中,Rin为锥体的初始旋转矩阵;Rp(t)为t时刻的旋转矩阵。
对于进动目标,Rp(t)=RcRs,Rc和Rs分别为锥旋旋转矩阵和自旋旋转矩阵。由Rodrigues公式[3]

式中,ωc为锥旋角速度矢量;Ωc=‖ωc‖;ω′c=ωc/Ωc,^ω′c为ω′c的反对称矩阵。

式中,ωs为自旋角速度矢量;Ωs=‖ωs‖;ω′s=ωs/Ωs,^ω′s为 ω′s的反对称矩阵。
设雷达发射线性调频信号,则目标回波信号可表示为

式中,rect(·)为矩形包络;Tp为脉冲宽度;fc为载频;γ为调频率;^t为快时间;tm=t-^t(m=0,1,…,M-1)为慢时间为发射脉冲序号。ρ(x,y,z)和R(x,y,z;tm)分别为目标上(x,y,z)处散射点的散射强度和在tm时刻的径向距离。
对回波进行解线频调处理后可得目标的慢时间距离像信号为

式中,RΔ(x,y,z;tm)=R(x,y,z;tm)-Rr,Rr为参考信号的参考距离。
2 非对称进动目标三维成像
2.1 进动目标微动参数估计
为实现进动目标的成像,需要首先分析并提取进动目标的微动参数。在式(1)~式(3)中,除与散射点初始位置相关的参数外,还包括4个未知量,分别为:锥旋角速度Ωc、锥旋单位矢量、自旋角速度Ωs和自旋单位矢量。以上4个参数决定了进动目标的微动特性。在4个参数中,Ωc可利用相关法或Hough变换[16]等方法进行准确获取;对于和Ωs,文献[14]研究了目标三维锥旋矢量的重构,并提取了目标的自旋周期。以上参数中,无法获取的只剩自旋单位矢量。因为锥体对称轴即为目标自旋轴,所以自旋轴单位矢量即为锥体对称轴初始时刻的单位矢量。下面本文给出一种的估计方法。
由于锥顶散射点P0位于锥体自旋轴上,因此P0不受自旋的影响,在式(1)中,Rp(t)=Rc。设雷达视线方向单位矢量为nl,则锥顶散射点在雷达视线方向的距离变化可表示为

式中,r0=RinrP为锥顶散射点在参考坐标系中的初始位置矢量。式(6)可进一步表示为
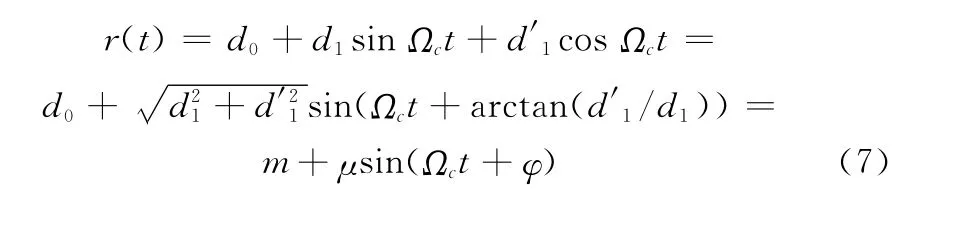
由式(7)可知,锥顶散射点的距离变化为正弦形式。在慢时间距离像中,利用H ough变换可以将锥顶散射点与尾翼散射点分离,并可提取正弦曲线的均值m、幅度μ和初相φ。

因为锥顶散射点位于锥轴上,因此r0的单位矢量即为自旋单位矢量=r0/‖r0‖。
2.2 三维成像
在获得微动参数Ωc,ω′c,Ωs和ω′s的基础上,本文提出一种基于三维逆投影变换的进动目标三维成像方法。
对于进动目标,式(5)中RΔ(x,y,z;tm)=(RcRsr)Tnl,其中r=[x,y,z]T为散射点在参考坐标系中的位置。利用Ωc,,Ωs,构造相位补偿因子

式中,r′=[x′,y′,z′]T为三维搜索参量。利用(x′,y′,z′;tm)对S(r,tm)作三维复数逆投影变换,即可得目标三维图像

对于目标上任一个散射点ri=[xi,yi,zi]T,当r′=ri时,在时间距离像上沿曲线ri(tm)=(RcRsri)Tnl进行相干叠加,则在三维空间I中,点(x′,y′,z′)=(xi,yi,zi)处将积累出峰值;而当r′≠ri时,时间距离像沿曲线r′(tm)= (RcRsr′)Tnl进行非相干叠加,在点(x′,y′,z′)处将不会出现峰值。设定合适的空间搜索范围,当遍历搜索空间中的任一位置,即可通过空间局部峰值检测的方法,重构出目标上强散射点的三维空间分布。
3 仿真实验
3.1 方法有效性仿真
为验证本文方法的有效性,进行以下仿真实验。仿真对象为图1所示的含尾翼进动锥体,长度3 m,底面半径1 m,锥旋频率1 Hz,自旋频率1 Hz,进动轴方向单位矢量[0-1 0],进动角20°。雷达发射载频为10 G Hz的线性调频信号,脉宽1μs,带宽2 G Hz,脉冲重复频率1 000 Hz,连续对目标观测1 s。目标回波产生采用动态电磁仿真的方法。首先对于锥顶散射点,考虑散射的各向异性,采用高频电磁计算的方法获得其雷达散射截面(radar cross section,RCS)[4];对于尾翼散射点,考虑遮挡效应,回波需要乘上遮挡因子

式中,r0×(r0×nl)为锥体轴线与雷达视线所成平面上垂直于锥体轴线的方向矢量;ri(tm)为第i个散射点tm时刻的位置矢量。之后结合第2节的目标进动模型,对静态RCS进行抽取,即可得到目标的动态电磁仿真回波。
图2给出了目标回波经dechirp处理后的慢时间距离像。从图中看到,锥顶散射点强度随慢时间作缓慢变化,反映了其RCS由视角变化引起的各向异性;各尾翼散射点由于主体遮挡,仅在半个周期内存在回波。

图2 目标回波慢时间距离像


图3 z′=0时x′y′平面搜索结果
图4仿真了对空间搜索结果的三维切面图。该图反映了目标强散射点在空间的三维分布情况,通过对空间中强点进行检测即可重构目标的三维结构。

图4 空间搜索结果三维切面图
为了避免图像中存在的旁瓣对强点检测造成干扰,需要设定合适的检测门限对旁瓣进行抑制。高的检测门限可有效抑制旁瓣干扰,但也可能影响对弱散射点的检测;而低的检测门限在提高弱散射点检测能力的同时,会增加噪声和旁瓣被检出的概率。因此需要综合考虑三维空间中噪声、旁瓣和散射点的相对幅度,从而选择合适的检测门限。图5仿真了检测门限为空间最强点幅度1/2时,z′=0平面的旁瓣抑制结果。从图中可以看到经检测门限后,较低的旁瓣得到很好地抑制,图像中只剩下幅度较高的峰值。

图5 z′=0平面的旁瓣抑制结果
对经过门限检测的空间数据进行局部极大值搜索,在三维空间中检测到5个局部极值,对应了目标在空间上的5个强散射点,据此可重构目标的三维结构,如图6所示。从图中看到,重构结果与仿真目标的外形结构一致,说明本文方法是有效的。

图6 目标三维重构结果
3.2 微动参数估计误差仿真
由于微动参数的估计可能不够精确,会导致目标成像质量下降,因此需要对微动参数估计误差对成像的影响进行分析。复数逆投影变换的核心是通过对回波进行相位补偿,使得同一散射点对应的时间距离曲线上的所有数据进行同相叠加。因此这里从参数估计误差对相位的影响入手进行分析。定义相位误差

从图7看出,相位误差随观测时间的增加而逐渐增大,因此,为减小微动参数估计误差对成像的影响应尽量缩短对目标的观测时间;同时,仿真结果还反映出相位误差受锥旋角速度和自旋角速度误差的影响相对更大,通过减小锥旋角速度和自旋角速度的估计误差也可有效提高成像质量。
4 结 论
非对称进动目标复杂的微动形式增加了其成像的难度。本文在估计目标微动参数的基础上,反演出目标的微动特性,进而利用逆投影变换的方法对目标三维空间结构进行重构。仿真实验验证了在微动参数估计较为精确时,该方法可准确实现目标的三维成像。
[1]Zhou W X.B M D radar target recognition technology[M].Bei j ing:Publ ishing House of Electronics Industry,2011.(周万幸.弹道导弹雷达目标识别技术[M].北京:电子工业出版社,2011.)
[2]M a L,Liu J,Wang T,et al.Micro-Doppler characteristics of sliding-type scattering center on rotationally symmetric target[J].Science China Information Science,2011,54(9):1957-1967.
[3]Yao H W,Wei X Z,Xu S K,et al.Micro-m otion characteristics of non-ideal scattering centers of midcourse targets with precession[J].Acta Electronica Sinic,2012,40(9):1844-1851.(姚辉伟,魏玺章,徐少坤,等.弹道中段进动目标非理想散射中心微动特性研究[J].电子学报,2012,40(9):1844-1851.)
[4]Bai X R,Bao Z.High-resolution 3 D imaging of precession coneshaped targets[J].IE E ETrans.on Antennas Propagation,2014,62(8):4209-4219.
[5]Zhang L,Li Y C,Liu Y,et al.Time-frequency characteristics based motion estimation and imaging for high speed spinning targets via narrowband waveforms[J].Science China Inform ation Science,2010,53(8):1628-1640.
[6]Ding X F,Fan MM,W ei X Z,et al.Narrow band imaging method for spatial precession cone-shaped targets[J].Science China Inform ation Sciences,2010,53(4):742-949.
[7]Pan X Y,Wang W,Liu J,et al.Modulation effect and inverse synthetic aperture radarimaging of rotationally symmetric ballistic targets with precession[J].IE T Radar,Sonar and Navigation,2013,7(9):950-958.
[8]Yuan B,Xu S Y,Liu Y,et al.Echo separation and imaging of spatial precession targets with unsym metrical appendix parts based on C E M D[J].Journal of Electronics&Inform ation Technology,2013,35(1):1-7.(袁斌,徐世友,刘洋,等.基于复数经验模式分解的非旋转对称空间进动目标回波分离及成像研究[J].电子与信息学报,2013,35(1):1-7.)
[9]Liang B S,Zhang Q,Lou H,et al.A method of three-dimensional imaging based on micro-m otion feature association for spatial asy m metrical spinning targets[J].Journal of Electronics& Information Technology,2014,36(6):1381-1388.(梁必帅,张群,娄昊,等.基于微动特征关联的空间非对称自旋目标雷达三维成像方法[J].电子与信息学报,2014,36(6):1381-1388.)
[10]Chen VC,Li F,Ho SS,et al.Micro-Doppler effectin radar:pheno menon,model,and simulation study[J].IEEE Trans. on Aerospace Electronic Systems,2006,42(1):2-21.
[11]Chen V C.The micro-Doppler effect in radar[M].Boston:Artech House,2011.
[12]Gao H,Xie L,W en S,et al.Micro-Doppler signature extraction fro m ballistic target with micro-motions[J].IE E E Trans. on Aerospace Electronic Systems,2010,46(4):1969-1982.
[13]Yao H Y,Sun W F,M a X Y,et al.Precession feature extraction of warhead with em pennages[J].Electronic Letters,2013,49(9):617-618.
[14]Luo Y,Zhang Q,Yuan N,et al.Three-dimensional precession feature extraction of space targets[J].IE E E Trans.on Aerospace and Electronic System,2014,50(2):1313-1329.
[15]Ning C,Huang J,Huang P K.Solution for characteristic parameters of precession cone-shaped target using H R RP[J].Systems Engineering and Electronics,2014,36(4):650-655.(宁超,黄璟,黄培康.基于HRRP的进动锥体目标特征参数求解方法[J].系统工程与电子技术,2014,36(4):650-655.)
[16]Zhang Q,Yeo TS,Tan H S,et al.Imaging of a moving target with rotating parts based on the hough transform[J].IE E E Trans.on Geoscience and Remote Sensing,2008,46(1):291-299.
Three-dimensionalimaging of precession targets with unsym metrical appendixes based on micro-motion parameters estimation
H U Xiao-wei,T O N G Ning-ning,H e Xing-yu,Jiang Dong,WANG Yu-chen
(Air and Missile Defense College,Air Force Engineering University,Xi’an 710051,China)
Imaging of precession targets with unsym metrical appendixesis a key challenge for spatialtargets imaging at present.The echo model of precession targets with unsym metrical appendixes is established.Based on that,4 micro-Doppler parameters needed forimaging are analyzed,and the corresponding parameters estimating method is given.With the parameters,a 3-D imaging method for precession targetsis proposed based on 3-D complex-valued back projection.Firstly,the phase compensation factor is structured with the parameters. Then a 3-D search is done in time-range profile,and the targets 3-D image is got afterwards.Finally,simulations verify the effectiveness of the proposed method,and analyze theinfluence of parameters estimating error to the imaging result.
precession targets with unsym metrical appendixes;micro-Doppler parameters estimation;3-D complex-valued back projection;3-D imaging
T N 957.51
A
10.3969/j.issn.1001-506 X.2016.03.04
1001-506 X(2016)03-0501-05
2014-12-29;
2015-08-22;网络优先出版日期:2015-09-18。
网络优先出版地址:http://www.cnki.net/kcms/detail/11.2422.TN.20150918.1532.004.html
国家自然科学基金(61372166);陕西省自然科学基础研究计划项目(2014J M 8308)资助课题
胡晓伟(1987-),男,博士研究生,主要研究方向为雷达目标成像与识别。
E-mail:601237134@qq.com
童宁宁(1963-),女,教授,博士,主要研究方向为雷达阵列信号处理。
E-mail:18092629021@189.com
何兴宇(1989-),男,博士研究生,主要研究方向为雷达目标成像。
E-mail:hxy_19890708@163.com
江 东(1991-),男,硕士研究生,主要研究方向为雷达目标成像。
E-mail:283945288@qq.com
王宇晨(1988-),女,硕士,主要研究方向为信号处理。
E-mail:13289322268@163.com
