一种基于DBF的反辐射导引头快速测向技术

李　翔，饶　鲜

(西安电子科技大学 电子工程学院，陕西 西安 710071)



一种基于DBF的反辐射导引头快速测向技术

李翔，饶鲜

(西安电子科技大学 电子工程学院，陕西 西安 710071)

为了提高反辐射导引头角度搜索的速度，文中提出了一种基于数字波束形成的快速测向技术。该技术基于折半查找的思想，将角度搜索问题转换为利用不同宽度的数字波束进行空间目标角度的折半查找问题。研究了该方法的基本原理，分析了其搜索速度和运算量。仿真结果显示，该方法在保证应有的测角精度与角度分辨力的条件下，解决了传统数字波束形成时侦测时间较长，且效率低的问题。

反辐射导引头；数字波束形成；快速测向技术

电子战中，反辐射导弹[1-3]是可摧毁敌方辐射源的一种杀伤性武器，其使得雷达系统由防御屏障转变为被攻击的目标。反辐射导引头是反辐射导弹完成对目标的捕捉以及跟踪的关键部件，测向过程中要求导引头有较大的瞬间视野、较高的测角精度和角度分辨力以及较快的测向速度。现代反辐射导引头常用的测向技术[4-5]包括比幅法测向、相位干涉仪测向以及比幅干涉仪测向等。比幅测向法算法简洁、结构并不复杂且价格低廉，但比幅测向系统的灵敏度以及测向精度等测向性会受到天线的极化方式、波束宽度、天线之间的张角等因素影响。干涉仪测向算法的关键问题是鉴相器的输出相位差测量值可能会出现模糊，而相位干涉仪测向系统最大无模糊视角范围与测向精度对基线长度要求存在着矛盾。

随着科技的发展，全数字波束形成技术因为良好的抗干扰能力和灵活性逐渐在反辐射导引头上得到应用。数字波束形成(DBF)[6]是相控阵天线与数字信号处理结合的产物，广泛地应用于阵列处理的领域，其无需模拟移相器和衰减器，在数字信号中形成波束，进而全面提升被动导引头的性能。传统的数字波束形成测向技术虽可得到较高的测角精度，但搜索次数与耗费时间却无法满足被动导引头实时测向的要求；而多波束形成[6]的DBF测向算法虽满足测角精度与速度要求，但计算量大且较为复杂，常采用FFT算法[7]减少运算量，但运算量仍较大，这两种方法均存在一定的缺陷。

本文主要在传统的数字波束形成测向技术基础上，为提高反辐射导弹在测向过程中的搜索速度，提出了一种基于DBF的反辐射导引头快速测向技术，这种方法既可兼顾测向精度、节省运算量，又可保证测向的时间要求，提高测角的效率。

1　数字波束合成原理

数字波束合成(DBF)的基本原理[8-13]如图1所示。

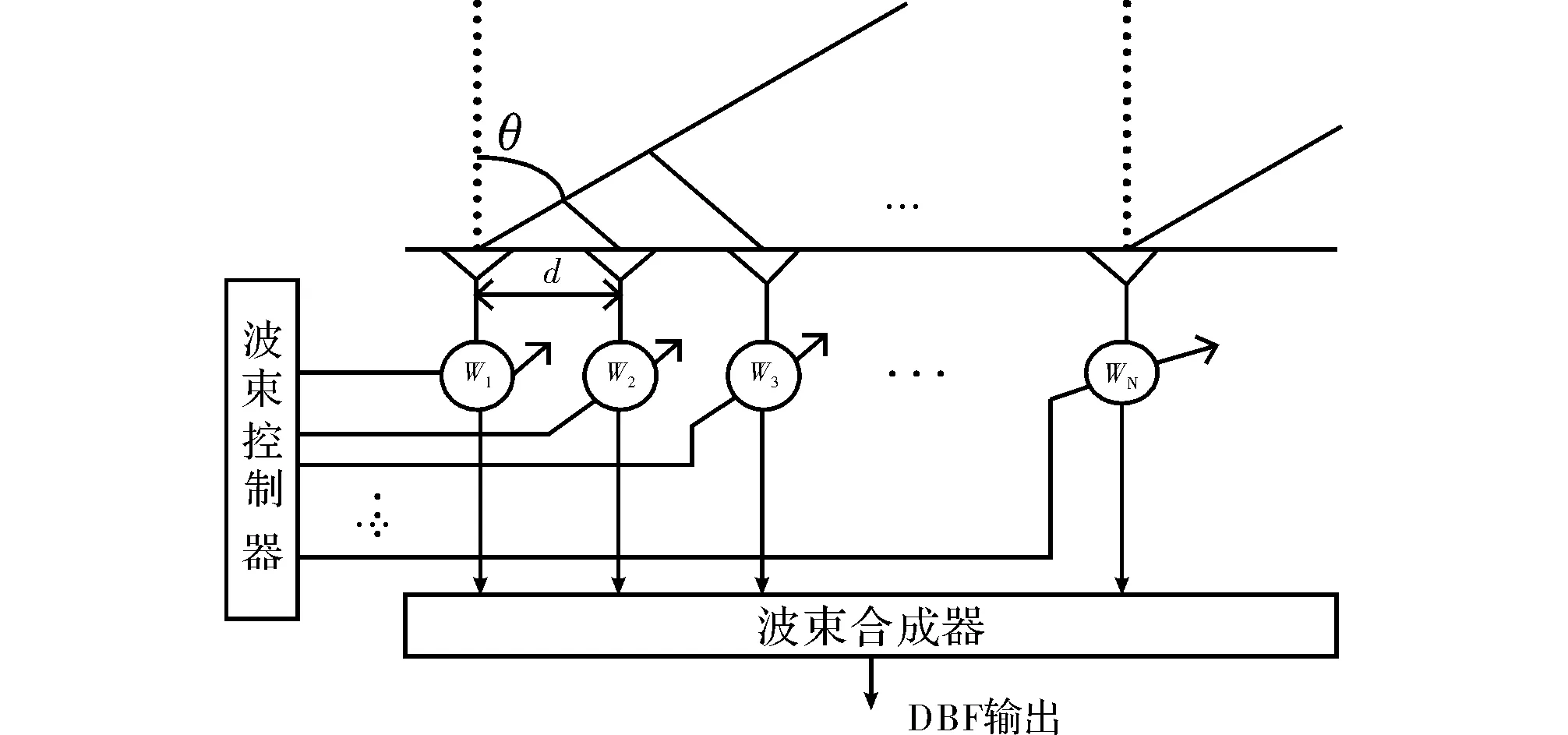
图1　DBF形成原理图

假设天线阵列是间距为d的N个阵元排列形成的等距离均匀线阵，以左边第一个阵元为参考阵元，接收信号为s(t)，信号的到达角度为θ,则第i个阵元所接收到的信号为

(1)

其中，n(t)为系统测量噪声。

将式(1)写成矩阵形式，则有

X(t)=A·s(t)+n(t)

(2)

系统的观测矢量为

系统噪声矢量为

系统的调相矢量为

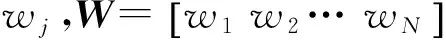
Y(t)=WT·X(t)

(3)

数字波束形成器输出的方向性函数为

(4)

由上述分析可知，DBF的实质是数字式空间滤波。由于信号矢量形式较为固定，只需通过改变加权矢量W不断调整波束方向和波束形状，便可达到对来波方向的波束指向，达到测向的目的。

要形成多个波束时，只需采用不同的加权矢量，分别求出其与阵列输出信号的加权和，即可获得不同指向的波束，这就是数字波束形成DBF的原理。在数字波束形成系统中，若形成m个独立波束，则有相应的m组加权矢量，其加权矩阵为W。

(5)

m个波束的输出为

(6)

由于多波束的数字波束形成的计算量较大，且计算较复杂，因此多采用快速傅立叶变化FFT的方法产生多波束。

2　快速测向技术原理

2.1快速测向技术基本原理

基于数字波束形成的反辐射导引头快速测向技术的核心是折半查找思想。在搜索空域内，利用数字波束形成技术在空域中心形成左右两个对称的波束，判定目标在空域的左侧或右侧范围后，再在该波束范围重复进行二分，直到达到了最小的波束宽度Δθ为止。运用这种方法，可经过几次二分之后快速地缩小范围定位目标并进行制导，因此可节省较大的计算量。

由理论可知，由N个天线阵元决定的雷达波束宽度为

(7)

根据折半查找思想，每进行1次二分之后需要的波束宽度是进行上1次二分需要的波束宽度的1/2，根据式(7)得到，每进行1次二分需要的阵元数是进行上1次二分需要的阵元数的两倍。

快速测向技术的原理如图2所示。

图2　快速测向技术的测向原理图

图2中，φi-1为上1次二分的波束中心指向，φil为本次产生的左波束中心指向，φir为本次产生的右波束中心指向，θi为本次的波束宽度。

该方法的实现步骤如下：

(1)赋初值。天线阵元数N0=1，波束宽度θ0=N·Δθ，波束指向φ0=0°；

(2)修正第i次搜索参数。天线阵元数为

Ni=2i·Ni-1

(8)

波束宽度为

(9)

左右波束指向分别记为φil与φir

(10)

应提供的天线阵内相位补偿值为

(11)

形成左右两个波束需要的对第p个单元通道的加权系数为

(12)

为在第i次二分时形成两个左右波束，接受信号的加权矢量Wi为

(13)；

(3)形成第i次的天线波束输出

(14)

(4)判断目标位于左右哪一个波束内。判决规则为sum(FI(1:))>sum(Fi(2:))判定：目标在左波束内；sum(FI(1:))≤sum(Fi(2:))判定：目标在右波束内；

(5)确定下1次二分的中心角度

(15)

(6)重复步骤(2)，直至到达所需要的最小波束宽度。

可以看出，这种技术每次只需要天线的一部分阵元进行测向，每次形成两个波束，运算量小，因此其优势主要集中在测向速度以及运算量上。

2.2快速测向技术性能分析

分析了快速测向技术的搜索速度和运算量，并在空间角度测量范围Ω=N·Δθ(N是以Δθ量化的角度范围)相同的前提下，分别在搜索速度上以及运算量上对比了传统的数字波束形成、多波束形成FFT算法以及快速测向技术3种方法的性能。

(1)搜索速度分析。搜索速度主要受搜索的次数影响。快速测向技术由于是折半查找方式，每一级运算产生两个波束，将角度范围成倍缩小直至最小角度分辨力为止，因此同样测角范围以及相同角度分辨力下，快速测向技术需要进行log2N级数字波束形成运算

T=log2N

(16)

传统DBF单波束测向算法由于形成单波束进行测向，要进行N级数字波束形成运算

T=N

(17)

N个天线的DBF多波束FFT算法中，根据FFT算法原理可知，需要进行log2N级运算。

3种测向方法测向搜索时的运算级数与量化测角范围的关系如图3所示。

图3　测向级数的关系对比

由图3所示，将快速测向技术与传统DBF单波束测向算法比较可知，快速测向技术与DBF多波束FFT算法可更加快速且高效地进行测向，在速度上有了大幅提高；

(2)运算量分析。快速测向技术由于前T-1次均未使用所有的天线，而是使用天线阵的一部分进行二分，每次产生两个波束，需要进行log2N次运算，且每次运算所需的乘法运算为前一次的1/2，所以其总的乘法运算量为

(18)

传统DBF单波束测向由于在空间范围Ω内需要形成N级运算，且每一级运算需要进行N次乘法运算，因此其乘法的运算量为

Q=N2

(19)

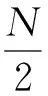
(20)

3种方法的乘法运算量关系如图4所示。

由图4可知，在角度范围不变时，天线数N值越大，快速测向技术节省的运算量就越多，优势就越明显。因此，根据对比结果可得出，快速测向技术在计算量的节省方面优势明显，这样就能提高运算的效率。根据运算级数以及运算量的分析可知，快速测向技术相较与传统的数字波束形成方法来说可大幅提高运算速度，减少运算量，提高运算的效率。更值得一提的是，二分法是一种将角度范围逐渐缩小的方法。因此，倘若辅助其他的算法结合使用，可大幅提高效率，或达到超分辨的能力，这也是今后进行更加深入研究的方向。

图4　3种测向算法的乘法运算量关系对比

3　仿真结果

由于反辐射导引头体积的限制，天线阵元数量通常不多。仿真时采用天线阵元数N=16，假设理论角度θth=16°，信号频率为9 MHz，根据频率可求得波长λ，为避免产生测角模糊，取d=λ/2，则角度分辨力Δθ=100/N，且整个测角范围Ω=N·Δθ。整个仿真过程需要的次数m=log2N=4。

首先仿真了4次二分的左右波束的波束合成图，如图5所示，其中实线都是右半波束，虚线均是左半波束。

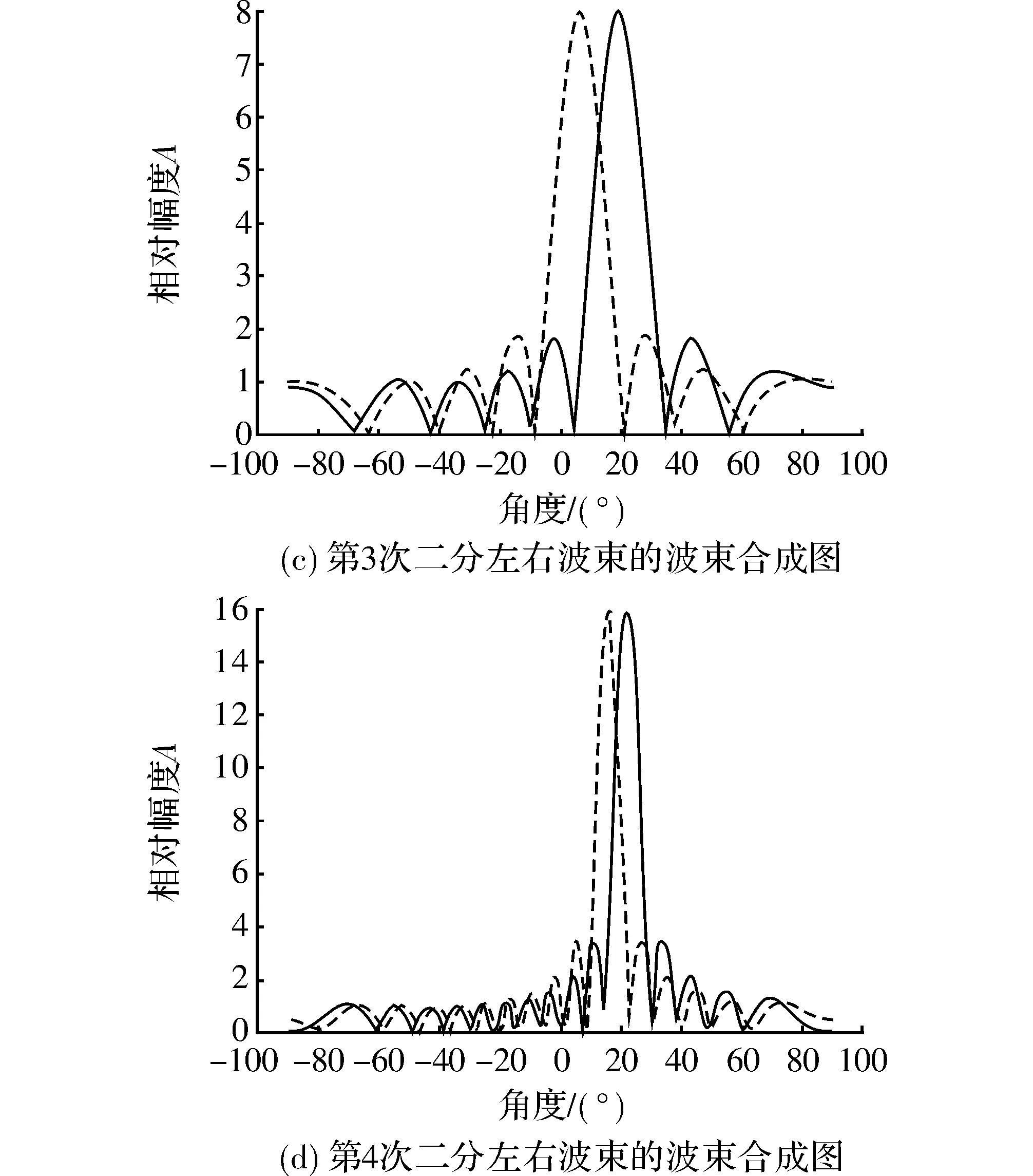
图5　SNR=13 dB时4次二分的左右波束的天线方向图

根据4次二分的波束合成图可得出：左右半边波束的输出在不同角度时均有不同的幅值，并可通过快速测向技术估计角度。

然后，仿真了每1次二分后左右波束的输出的幅值关系，如图6所示，其中实线都是右半波束，虚线均为左半波束。

由于加入了噪声，可看到信号的波动，但幅度仍有大小之分，可通过快速测向技术确定估计角度。

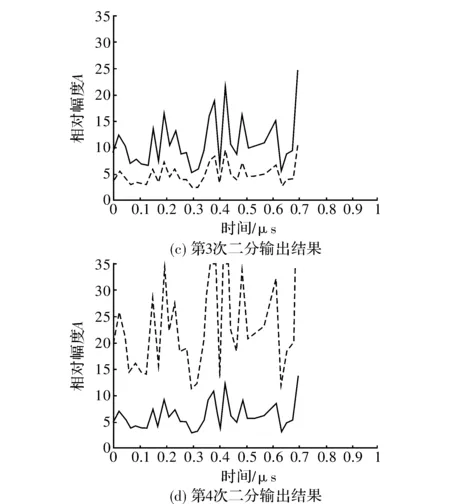
图6　3次二分输出的波形

然后，验证了角度估计的准确性，由仿真结果可知θes=15.625°，与理论分析结果一致。

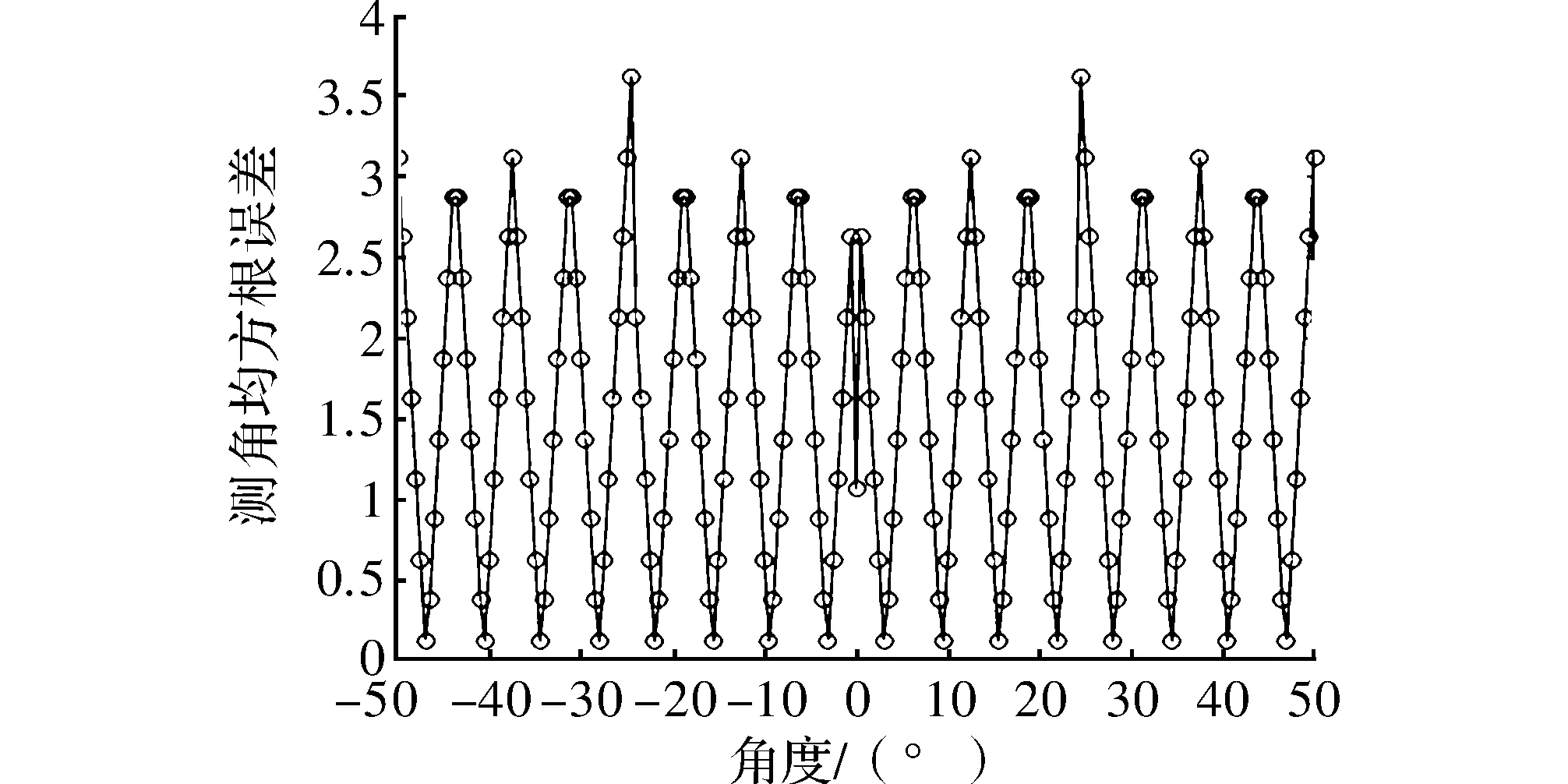
图7　不同角度下的均方根误差

根据仿真结果可得到：由于4次二分之后使得角度对准的点分别为：±3.125°，±9.375°，±15.625°，±21.875°，±28.125°，±34.375° ，±40.625°，±46.875°，因此越接近这些值时均方误差越小，由于文中取的间隔为0.5°，因此取不到最小值，与理论相符。

4　结束语

本文在基于反辐射导引头的应用背景下,针对传统的数字波束形成(DBF)测向算法速度慢的问题，提出并讨论了一种基于数字波数形成的快速测向技术的测向新思路，其主要思想是折半查找，即在展宽的角度范围内利用DBF测向原理形成两个波束并判定其所在波束区域，再在判定的区域内进行第2次二分，依次类推，直至达到最小的角度分辨力。这种方法相较于传统的测向方法而言在一定程度减少了计算量，测向速度快，且测角的稳定性良好，分析了快速测向技术的性能并与传统方法进行了比较。最后进行了仿真实验，验证了此方法的可行性。

[1]吕彤光.被动雷达导引头抗干扰技术研究[D].长沙:国防科学科技大学,2001.

[2]曲长文.反辐射导弹被动导引头分析[J].制导与引信,1997(1):33-37.

[3]王艳奎.反辐射导引头技术发展分析[J].飞航导弹,2009(3):39-44.

[4]邵姚定.宽带被动导引头技术的分析[J].制导与引信,1995(3):27-39.

[5]刘东文.反辐射导引头宽带测向技术研究[D].西安:西安电子科技大学,2014.

[6]赵国庆.雷达对抗原理[M].2版.西安:西安电子科技大学出版社,2012.

[7]王海峰,吴宏宇.被动雷达导引头发展历程及技术综述[J].飞航导弹,2013(1):78-80.

[8]刁晓静.电子侦察中的宽带DBF技术研究[D].西安:西安电子科技大学,2011.

[9]胡可欣,胡爱明.数字波束形成技术(DBF)在雷达中的应用[J].现代防御技术,2006,34(6):103-106.

[10] 张新胜.DBF技术在雷达领域中的应用[J].雷达科学与技术,2004(5):267-269.

[11] 王霖郁,司违建.利用DBF与MUSIC算法结合进行测向[J].弹箭与制导学报,2008, 28(3):68-70.

[12] 余锐.宽带DBF和数字信道化技术[D].西安:西安电子科技大学,2009.

[13] 王杰贵.应用于雷达电子战系统的宽带DBF技术[J].航天电子对抗, 2006, 22(5):39-41.

Fast Direction Finding Technology for Anti-radiation Seeker Based on Digital Beam Forming

LI Xiang, RAO Xian

(School of Electronic Engineering, Xidian University, Xi’an 710071, China)

A fast direction finding technology based on digital beam forming is proposed for the angle searching of anti-radiation seekers. The problem of angle searching is converted into the binary angles searching in space using digital beam with different widths. The basic principles, the speed and the amount of computation of this method are studied. The simulation results show that the searing time casting and efficiency are improved by the proposed method while keeping the same angle measurement accuracy and resolution.

anti-radiation seeker; digital beam forming; fast direction finding technology

10.16180/j.cnki.issn1007-7820.2016.08.014

2015-11-03

中央高校基本科研业务费专项基金资助项目(JDYB140810)

李翔(1990-)，男，硕士研究生。研究方向：电子对抗等。饶鲜(1976-)，女，副教授，硕士生导师。研究方向：雷达/通信辐射源无源定位技术，高分辨雷达干扰技术等。

TJ765.3

A

1007-7820(2016)08-046-05