超声变幅杆的理论设计与ANSYS仿真分析

2016-09-19山西中北大学山西省先进制造技术重点实验室常小龙

河北农机 2016年3期

关键词：变幅换能器振幅

山西中北大学山西省先进制造技术重点实验室　　常小龙

山西中北大学山西省先进制造技术重点实验室常小龙

本文以超声波的传播原理为理论基础，根据牛顿定律得到变截面杆纵振动的波动方程。并由此计算了圆锥阶梯型复合超声变幅杆的尺寸，并用ANSYS软件对所设计的变幅杆进行模态分析及谐响应分析，验证了理论设计的合理性。

超声变幅杆；ANSYS模态分析；谐响应分析

在超声波加工中，变幅杆作为一个重要的部分，主要起两个作用，即把放大振幅和超声振动传递给负载［1］。超声波引起变幅杆内各质点按正弦规律沿超声的传递方向在原地做往复振动，并传导到工具端面，使工具端面做超声频振动［2］。

1　超声加工的原理

由超声波发生器将220V或380V的交流电转换成有一定功率输出的超声频电震荡信号传递给换能器，再由换能器将高频震荡信号转换成高频机械振动后传递给变幅杆，经变幅杆将振幅放大后（0.05～0.1mm）传递到工具头，利用工具头在有磨料的液体介质中产生磨料的冲击、抛磨、液压冲击及由此产生的气蚀作用来去除材料［3］。

2　变幅杆的设计

2.1理论设计

超声换能器压电陶瓷在电场的作用下的伸缩为0.005～0.01mm，加工中要求工件或者刀具的振幅必须达到0.01～0.02mm［4］，必须对振幅进行扩大，因此变幅杆的设计成为实验的关键，通过比较不同截面形状变幅杆纵向振动的固有频率和理论频率，试验需要有较大放大系数且稳定性好的变幅杆，考虑设计圆锥阶梯式的复合变幅杆。

其中：S=S（x）为杆的横截面积函数；ε=ε（x）为质点位移；k=k为圆波数，ω为圆频率为纵波在细棒中的传播速度，ρ为杆材料的密度，E为杨氏模量。

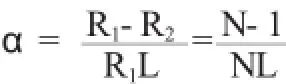
其中：R1、R2分别为复合变幅杆的大、小端半径；L为变幅杆总长度。

放大系数为：

其中：A1、A3分别为大小端的振幅；L1、L2、L3分别为复合变幅杆三段的长度。

R1的尺寸与选择的换能器尺寸相同，对于选定的换能器，其为确定值；R2是变幅杆的端部尺寸，由所需的振动振幅确定；通常复合变幅杆首先确定两端L、L的尺寸，取，L的变化122对放大系数和纵振频率影响很大，一般取值在50mm以内［5］，本设计取L2=30mm。

在变幅杆内部开D=10mm、L为杆长的通孔，用于安装换能器和工件。

材料选取45钢，疲劳强度高且易加工，性能参数如表1所示。根据以上公式及分析，可以得到圆锥阶梯型复合变幅杆的设计参数如表2所示。

2.2变幅杆模态分析

将工具头和变幅杆做整体分析，忽略两端螺纹孔的影响。在ANSYS中建立的三维模型，采用SOLID单元Block Lanczos法计算，通过提取10阶模态，频率范围为18～25kHz，得到如图1所示结果。

图1　模态分析结果

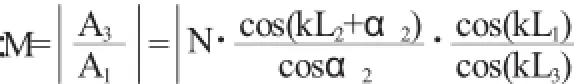
*国家自然科学基金（51275490）

表1　变幅杆材料特性

表2　变幅杆的设计参数

图3　五阶模态分析X方向位移图

通过图2和图3所示结果分析，可以看出当共振频率为20080Hz时，变幅杆在法兰盘处的位移最小，而在小端面处的位移振幅最大，五阶振动模态为超声电火花加工所需的纵向振动，其仿真结果与理论设计频率基本吻合，从而验证了所设计变幅杆尺寸的合理性。

2.3变幅杆谐响应分析

图4　变幅杆总位移云图

图5　变幅杆X方向位移云图

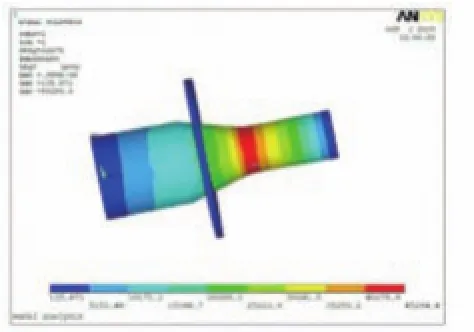
图6　变幅杆压力云图

采用full法及Sparse slover求解器，扫描范围为18～23kHz，子步数为20，在变幅杆大端为5μm，由图4、5可知，在20075Hz的激励下，X方向的位移和总的位移分别从大端到小端逐渐增大，但是在法兰盘处达到最小。图6可以看出圆锥形和小端阶梯型过渡处应力达到最大，而在法兰盘处应力最小，与理论设计相符合，满足试验要求。