汽车盘式制动器的优化设计

山东德州学院汽车工程学院　　冯衍辉

汽车盘式制动器的优化设计

山东德州学院汽车工程学院冯衍辉

当今社会汽车已成为人们最主要的交通工具，为了保证驾车安全，现在汽车都普遍采用盘式制动器，而盘式制动器的工作性能是整个制动系中最复杂、最不稳定的因素。为提高制动系统的性能，采用优化设计建模、遗传学算法以制动减速度、制动力矩为优化目标进行优化设计。

盘式制动器；制动力矩；优化设计

前言

盘式制动器以其诸多优越性广泛应用于汽车制动系统中，例如：涉水后仍能保持稳定的制动力矩和制动稳定性、在制动过程中产生的制动力大并且稳定、在各种路况下都能够产生稳定的力矩，适用范围广泛、盘式制动器能够和空气直接接触，故盘式制动器的散热性很好。盘式制动器也有其缺点，例如：摩擦片和盘片之间的尘土对摩擦盘的磨损严重、制动效能低、所需制动管压力较高、制动结构复杂。为了提高盘式制动器的制动性能和制动效率，我们在满足必须的性能指标和约束条件下对制动器进行优化设计［1］。本文采用最优优化设计为理论原则，对汽车盘式制动器的设计方案进行全方位的优化设计研究和实践，从而设计出高性能的盘式制动器。

1　盘式制动器基本特性分析

1.1盘式制动器制动力矩的分析与计算

假设摩擦片的整个摩擦表面和制动盘完全接触，并且在接触处所受单位压力分布均匀，则制动器在制动过程中产生的制动力矩为：Mρ=2ρPR

其中ρ——摩擦系数，一般ρ=0.35，在理想条件下ρ可取0.3，使计算结果符合实际情况。

R——受力半径

对于一些常见的摩擦片的表面，如果其具有相对较小的径向宽度，那么取R等于有效半径Re，在实际应用过程中是很准确的［2］。

平均半径：Rm=R1+R2/2

其中R1和R分别为摩擦衬片的内半径和外半径。

有效半径：Re=Mρ/2ρP

1.2制动器摩擦片所受的压力

假设摩擦片上任意一点到制动盘轴线的距离为r，在这段距

离范围内的摩擦片任一点所受压力P为［3］：

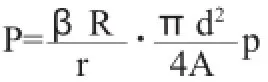
由上式可知，在R1和R2处，P分别达到最大值和最小值。摩擦片的最大的单位压力为：

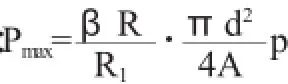
2　盘式制动器优化设计模型建立

2.1目标函数的建立

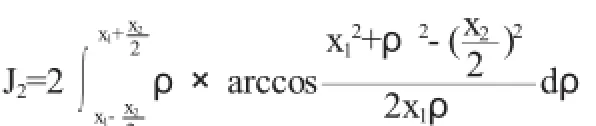
2.2约束条件

（1）在制动过程中制动减速度应大于等于国家标定的最小许用减速度a≥［amin］。制动时热衰退率φ一般为［0.25%］。

（2）摩擦片和制动盘间的空间约束应小于等于最大空间间隙即：0≤Dzp0/2-Dmp0≤Δ。

（3）制动盘温升ΔT≤［ΔT］，根据实际使用经验一般取［ΔT］=250℃。

（4）制动液压力p应小于等于制动系统压力极限值p≤［p］，［p］应在实际使用工况中取值。

3　优化算法

采用遗传学算法来研究追寻最优的解决方案。遗传学算法是模拟自然选择的遗传学机理计算生物进化过程，我们可以通

3.1算法设计流程图

如图1所示。

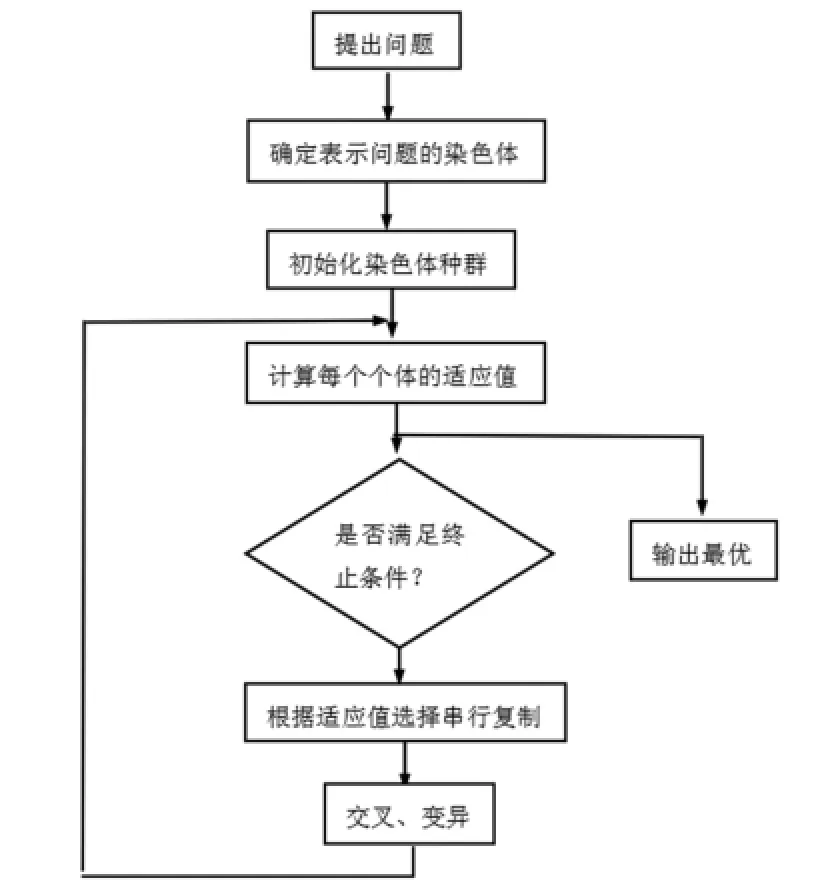
图1　算法设计流程图

3.2离散变量的处理

假设离散变量的值为 1，1.5，2，2.5，3，3.5，4，5，6，8，10，······。由此我们可以看到，如果采用统一的编码来表示，我们不能很准确地进行描述。因此，我们只能采用对应关系原则进行表示。

在设计的优化问题中只有取值在1～10之间，那么可取的值共有10个，所以二进制数的位数为l=4，并且其中有5个多余码。在处理这些多余码的过程中，如果我们采用调整编码精确度的方法进行处理是解决不了问题的，只能采用在多余的二进制编码中重复填写可取值的方法来解决这个问题。在经过处理后，得到的编码在解码的过程中二进制代码就和变量值具有了对应关系，这这种方法在无形中提高了变量值被选中的概率［5］。

3.3建立适度函数模型

遗传学算法适用于求函数极大值（极小值）的无约束最优化

问题，因此，需将原来的约束问题转化为无约束问题，设r1为惩

建立这样一个函数模型，我门可以将极小值问题转化为极大值问题，设Dmax是进化过程P（x）的极大值，则建立的适度函数为：f（x）=Dmax-P（x）。

3.4确定最终的求解结果

在MATLAB的操作环境下，采用遗传学算法编辑程序进行研究问题的优化求解，其结果如下：

X*=［0.080，0.060，0.040，0.062，0.020，3.243×107］

f（X*）=0.00873。

结果表明，优化后的目标函数值比原来设计的下降了80%，制动力矩显著增加，制动时间也缩短了，同时在制动过程中由于制动盘半径增大导致制动温度升高，但是温度升高值都在允许的范围内。

4　结论

盘式制动器在汽车制动系统中的应用日益增多，因此对盘式制动器的优化研究也是从未间断过的。由于其具有广泛性和结构形式的多样性，所以很多研究人员选择的研究方向和研究方法都不尽相同。针对盘式制动系一些制动力矩不足、制动温升不足等性能现状，我们以缩短制动时间和降低制动温升为目标进行了研究分析，在研究过程中我们采用遗传学算法选择合适的函数假设，最后得到了比实际值更好的优化值。

［1］姜平，黄文娟.基于MATLAB的盘式制动器优化设计［J］.机械工程与自动化，2007，34（6）：160～161.

［2］陈立周.机械优化设计方法［M］.北京：冶金工业出版社，2005.

［3］田福祥.盘式制动器的摩擦片压力和制动力矩［J］.工程机械，1998，32（10）：15～17.

［4］沈荣华，邹定平，黎桂英.汽车盘式制动器优化设计［J］.机械研究与应用，1999，12（1）：9～21.

［5］刘惟信.汽车制动系的结构分析与设计计算［M］.北京：清华大学出版社，2004.

冯衍辉，1993年1月出生，山东济宁人，本科在读。过这种模拟自然选择的进化过程寻求最优的方法［4］。