当逐差法遇上奇数段位移时数据该如何取舍

李研海

(吉林省永吉实验高中　吉林 吉林　132200)



当逐差法遇上奇数段位移时数据该如何取舍

李研海

(吉林省永吉实验高中吉林 吉林132200)

利用打点计时器打出的纸带求加速度，当逐差法遇上奇数段位移时，如何取舍数据，本文进行了大胆的猜想与探究，并提出新的主张.

逐差法奇数坏数据

1　问题提出

利用打点计时器打出的纸带求加速度，在高中阶段通常有算术平均值法、逐差法和图像法.不过，目前在一些教辅图书中几乎都采用逐差法，那么，当逐差法遇上奇数段位移时该如何取舍呢？

所谓逐差法就是分组求差法，在利用逐差法求加速度时，若纸带计数点间的间隔为奇数段时，通常需舍弃一个数据，化奇为偶后再分组求差.究竟舍弃哪个数据却众说纷纭，莫衷一是.有人认为，应去掉首段数据(以下简称“去首法”)，理由是首段位移长度最小，相对误差较大；多数人主张，应舍掉中间段位移(以下简称“舍中法”)， 其理由是这样可以增大测量量之差.难道舍弃末尾段位移(以下简称“弃尾法”)不行吗？不同的取舍方法，所得的结果不尽相同，那么舍弃哪一个数据计算误差会更小，误差的主要原因又是什么呢？“舍中法”真的最佳吗？

2　猜想探究

2.1误差猜想

笔者认为“弃尾法”也未尝不可.究竟哪种方法更准确，不能一概而论，关键在于舍弃的数据是否是“坏数据”.

值得注意的是，虽然都是利用打点计时器打出的纸带求加速度，但是不同的实验目的引起误差的原因是不同的.例如“研究匀变速直线运动”实验，误差主要来源于位移s的测量，无需考虑阻力的大小，因为它是求物体在合外力作用下的实际加速度.而“用打点计时器测重力加速度”实验，阻力的大小则为误差的主要来源.无论哪种情形，“坏数据”都是造成误差的罪魁祸首.

那么，坏数据是如何产生的呢？利用打点计时器的纸带求加速度，其误差主要取决于实验的偶然误差大小，而不是数据处理方法.研究发现，影响间接测量量(加速度)结果的最主要因素，是有的实验数据偏差过大.在诸多因素(交流电频率波动、长度测量、各种阻力等)中，主要是限位孔的阻力，其次是位移测量的偶然误差，而交流电频率波动的影响是可以忽略不计的.因为物体运动过程中，纸带不可能总保证与限位孔平行顺利地通过，纸带时常歪斜、扭曲甚至打卷，这势必造成阻力不均，使得某些数据点偏差过大产生“坏数据”，这样的坏数据参与求加速度的运算，势必造成较大的误差，倘若舍弃的恰好是坏数据，误差自然会减小.假如物体所受阻力均匀且无测量误差，当相邻计数点间距离之差Δs为一常量，反映在速度图像上，所有数据点均在一条直线上，无论用哪种取舍方法，所得结果都是一致的.

2.2图像探究

为避免有数据编造之嫌，防止以偏概全之疑，现以简便直观的v-t图像做一般分析，因为图像法的线性拟合既有取平均值的效果，还有助于剔除坏数据.

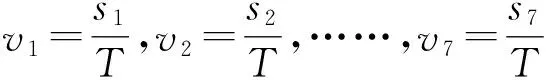
由图像不难看出，对于奇数个计数点， 假如数据点4偏离直线很远，则采用“舍中法”最好；如果数据点1偏离直线很远，则采用“去首法”更佳；倘若数据点7偏离直线很远，则采用“弃尾法”为妙.如果处理数据时剔除的恰好是“坏数据”，便可以有效地减小误差.

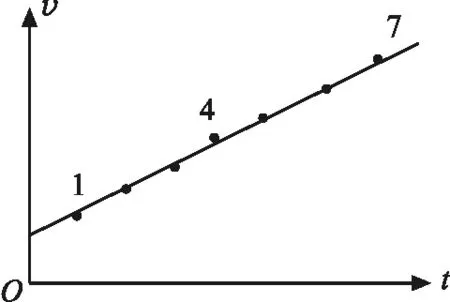
图1

可见，用逐差法处理实验数据时，采用哪种方法计算结果更准确，不在于数据取舍方法，而取决于舍弃的数据点是否为坏数据.或许有人会说，在没有画出图像的前提下，我们并不知道哪个是坏数据.的确，这纯属偶然，因此笔者说无论舍中还是弃端(去首、弃尾)均无绝对优势.

3　笔者之见

3.1数据处理

笔者认为，对于纸带上给出相邻计数点间奇数段位移时，也可以不舍弃某一数据，而利用全部数据直接作差.例如给出7个数据，设相邻计数点间的时间间隔为T，位移依次为s1，s2，…，s7，则

s4-s1=3a1T2

s5-s2=3a2T2

s6-s3=3a3T2

s7-s4=3a4T2

由此得

当然也可以写成

可见，前者所有7个数据全部得到了利用，而后者利用了6个数据，与舍中法无异，那么应如何测量数据呢？

3.2测量问题

对于打点计时器打出的纸带的数据测量可有3种方法：

一是起点测量，即一次性测量计数起点到其他各计数点的距离，设纸带上计数起点到其他各计数点的距离依次为d1，d2，d3，d4，d5，d6，d7，由此可求出相邻计数点间的位移为

s1=d1

s2=d2-d1

s3=d3-d2

s4=d4-d3

s5=d5-d4

s6=d6-d5

s7=d7-d6

二是逐段测量，就是依次测出相邻计数点间的位移s1，s2，…，s7，出于计算的方便和减小相对误差考虑，一般不主张用此法测量.

三是两段测量，亦即直接测出前后两大段位移，如上例的(s7+s6+s5)与(s3+s2+s1)或(s7+s6+s5+s4)与(s4+s3+s2+s1)，后者中s4似乎不起作用，但是这样可以增大测量量进而减小测量的相对误差.

实验纸带的数据究竟如何处理，应视具体情况而定.如果是自己测量实验数据，采用两段测量法最优，为了减小测量误差，可以多测几次取平均值代入公式进行计算.如果是考试做题，则别无选择，通常都是以起点测量或逐段测量形式给出数据.

大多数人主张起点测量法，且认为起点测量法会减小测量的相对误差.笔者认为，这倒未必，关键在于计数点的选取，要具体问题具体分析.比如我们要测量5楼窗户的高度，没必要先测出这个窗户的上下沿距地面的高度再作差，更不需将窗户分成几段测量再求和，最好的方法就是直接测出这个窗户上下沿的距离.

3.3创新主张

多数人认为，用逐差法求加速度，数据能得到充分利用,从而可减小误差.其实，数据的充分利用并不等价于数据全部参与，也不意味着一定能减小误差.表面上看，逐差法能充分利用实验数据，那是对逐段测量而言的，若采用起点测量，其实它也只利用了2～3个数据而已.笔者认为，就求加速度而言，两段测量法最优，即便是逐差法遇上奇数段位移，也无需舍弃数据.当然，起点测量法和逐段测量法除了能求加速度外，还可以判断物体是否做匀变速运动及求出各计数点的速度.

当纸带上给出相邻计数点间的位移为奇数段形式，欲利用逐差法计算加速度时，无论舍中与弃端，都只是实验数据的利用问题，由此产生的误差纯属偶然.当任意连续相等时间间隔内的位移之差Δs相等时，无论舍弃哪一数据，结果都相同；当Δs不等时，不同的取舍方法，所利用的实验数据不同，可能导致结果各异，只有当所舍弃的恰为“坏数据”时，误差才最小.那么与其纠缠纸带的数据处理，倒不如从减小误差上多下功夫，倘若取多条纸带求加速度平均值会更好一些.这正是：纸带数据奇数形，舍中弃端皆可行.数据不舍可全用，自行测量酌情定.

1杜志建.试题调研高考突破难点100讲 物理(修订版).乌鲁木齐:新疆青少年出版社,2012.7

2戴耀东.探究逐差法处理纸带时奇数段位移该如何取舍.物理教师,2013(12):52～54

3卢炜杰，吴先球，王笑君.三种实验数据处理方法的误差分析和教学探讨.物理教学,2013(12):22～23

4魏兴文，魏延博.对逐差法求加速度的质疑.中学物理教学参考，2013(9):30

2016-03-25)