例说“组合方块模型”中的摩擦力问题

林 宁

(江苏省东台中学　江苏 盐城　224200)



例说“组合方块模型”中的摩擦力问题

林 宁

(江苏省东台中学江苏 盐城224200)

“组合方块模型”考查的是多个方块的整体运动，或是先整体运动而后可能出现运动分离的情形，所涉及的知识主要有牛顿运动定律和功能关系，难点在于过程中对研究对象的把握及摩擦力的变力做功问题，适当情形下还要突出重心研究的意识.因此，这类题目知识点分布多，思维灵活性大，综合能力要求高，很有参考研究性.现赏析几例，以为抛砖引玉，望引起高度重视.

1　把握“整体归一”思想 发散能力突出求解方法

【例1】如图1所示，n个完全相同、边长足够小且互不粘连的小方块依次排列在一起，其总长度为l，总质量为M，它们一起以速度v在光滑水平面上向左滑动，某时刻开始滑上粗糙水平面．小方块与粗糙水平面之间的动摩擦因数为μ，若小方块恰能完全进入粗糙水平面，则摩擦力对所有的小方块所做功的数值为

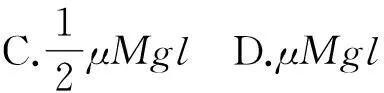
图1

解析：以所有方块为整体(相当于一个大方块)，根据题意,可有两种方法求出摩擦力所做的功.

方法1：由动能定理

可得A符合要求.

方法2：根据摩擦力的变力做功特点有

可得C符合要求.

所以该题答案选A,C.

点评：这n个小方块在滑上粗糙水平面前，相互之间没有弹力，进入后才有弹力，在研究时必须把它们看成一个整体(相当于一个大方块).由于它们进入粗糙水平面的长度在发生变化，所受到的摩擦力大小也在变化，并且摩擦力的大小与方块整体滑入的长度成正比，因而摩擦力做功的大小可根据平均摩擦力的大小或f-x图像来计算.当然，对于摩擦力大小变化的问题，我们通常要优先考虑用牛顿第二定律和功能关系.此题学生如果不注意从多角度来分析，很容易漏选答案.

2　扣准“合分状态”条件 明确运动突显功能关系

【例2】如图2所示，倾角为θ的斜面与足够大的光滑水平面在D处平滑连接，斜面上有A，B，C三点，AB间距为2l，BC和CD间距均为4l，斜面上BC部分粗糙，其余部分光滑．4块完全相同、质量均匀分布的长方形薄片，紧挨在一起排在斜面上，从下往上编号依次为1，2，3，4，第1块的下边缘恰好在A处．现将4块薄片一起由静止释放，薄片经过D处时无能量损失且相互之间无碰撞．已知每块薄片质量为m，长为l，薄片与斜面BC间的动摩擦因数为tanθ，重力加速度为g．求：

(1)第1块薄片下边缘刚运动到B时的速度大小v1；

(2)第1块薄片刚好完全滑上粗糙面时的加速度大小a和此时第3,4块间的作用力大小F；

(3)4块薄片全部滑上水平面后，相邻薄片间的距离d．

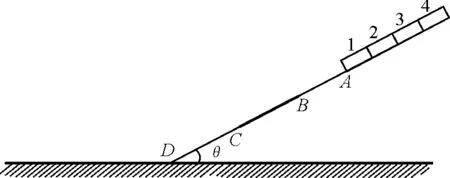
图2

解析：(1)以第1块薄片为研究对象(也可以4块为整体来研究)，根据动能定理有

得

(2)一旦第1块薄片滑上粗糙斜面，各薄片之间便有了弹力，以4块薄片为整体，有

4mgsinθ-μmgcosθ=4ma

得

以第4块薄片为研究对象，有

mgsinθ-F=ma

(3)设4块薄片全部滑上粗糙面时速度大小为v2，对A到C的过程，有

由于μ=tanθ，所以当第1块滑出C后，将沿斜面向下加速运动，其他3块仍在BC上一起匀速下滑，然后依次分离，重复1的运动.设每块薄片滑到水平面时速度为v3，注意重心变化，对C到D的过程，有

由于相邻薄片到达水平面时的时间差

得

点评：第(3)问的设计巧妙，但要求较高．这里首先要解决好4块薄片刚好全部滑入时的速度；其次要判断好4块薄片分别滑出时的运动状态、分离条件及相互滑出的时间间隔；最后还要解决好每块薄片滑到水平面时的速度．学生要能冷静思考，分析到位，才能高质量地解好此题．尤其是两次对不同对象用好功能关系，特别是方程中摩擦力做功的正确表达，更是对学生思维应用能力的一种重点考验．

从以上两例的分析可知，“组合方块模型”中的摩擦力在物体的运动和功能关系中扮演着非常重要的角色，同时这也恰恰是学生在应用中最为薄弱的环节．高考的命题有方向，但往往都会设置情境，来考查学生对知识综合的通透能力．作为教师，我们更要从“教与学需求”的高度去潜心思考和研究，才能让学生全面学习，轻松走向成功．

2016-03-21)