湖南省人均GDP的模型建立与分析

张锐　姚晗

湖南省人均GDP的模型建立与分析

张锐姚晗

人均GDP是体现一个地区发展状况的综合指标。本文针对湖南省历年人均GDP数据构建混合时序模型，并预测下年人均GDP数值，揭示该省人均GDP的潜在发展规律，以此为地方政策的制定提供理论依据。

人均GDP；时间序列模型；ADF单位根检验

一、引言

人均GDP既考虑了经济总量的大小，又很好的结合了人口因素的影响，所以它较为真实直观的反映了一个国家或地区的发展水平，是一个很重要的经济指标。因此深入分析该指标的增长趋势、波动规律有助于制定相应的宏观政策。

因为时间序列模型是依据自身数据出发研究其潜在关系，所以本文选取时间序列模型对湖南省人均GDP值进行预测。本文针对湖南省1978-2012年人均GDP数据用Eviews统计软件进行分析，并根据其内在联系给出了相关模型和预测结果。

二、混合时序模型

（一）ARMA（p，q）模型

假定时间序列中部分是自回归，部分是滑动平均，我们可以得到一个相当普遍的时间序列模型。一般来说，如果称｛xt｝为自回归滑动平均混合模型，简记为ARMA（p，q）。从一般表达形式可看出数据xt既和其滞后序xt-i（i=1，2 …p）列有关，也和滞后序列的误差εt-i有关。此模型针对平稳序列，否则应先对原序列进行处理，使其平稳后再进行模型建立。

（二）ARIMA模型

若某一时间序列为非平稳序列，但进行d次差分后变为平稳序列，则有如下定义：若一个时间序列的d次差分是一个平稳的ARMA过程，则称为自回归滑动平均求和模型。若yt服从ARMA（p，q）模型，我们称是ARIMA（p，d，q）过程。ARIMA（p，d，q）模型的实质就是将ARMA（p，q）模型和差分运算进行组合。

（三）混合时序模型

本文用传统时序分析方法提取确定性因素，但只有确定性因素是不够的，因为时序中还存在一些系统性因素以外的随机变动因素，这些是不能用普通时序方法来分析的。随着经济增长，随机因素在经济现象中所占比重逐渐加大，并且这些随机因素呈现一定的规律性。因此我们在实际分析中应将传统时序分析方法和随机分析方法结合起来建模，以此达到对时间序列信息的充分提取。因此本文拟建立混合时序模型，先用传统时序方法模拟人均GDP序列中的确定性影响因素，拟合后所存在的误差项反映的是其他一些随机因素的综合影响，它不满足随机误差的经典假设，会导致参数估计没有意义。所以本文对于误差项再采用ARMA模型进行拟合，以此来消除一般时间序列存在的序列相关性，以此达到修正传统时间序列模型的目的。本文用的混合时序模型如下：

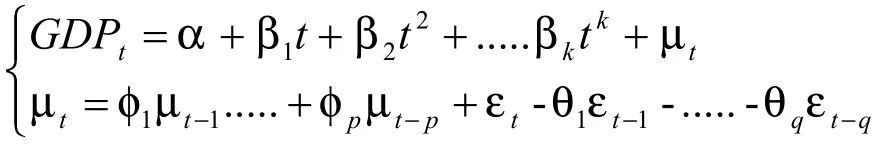
其中εt为白噪声，μt为误差项。

三、湖南省人均GDP预测模型的建立与分析

（一）样本的选择

本文利用湖南省1978-2012年的人均GDP数值进行研究，数据由《湖南省统计年鉴》整理得到。数据走势图呈现指数增长。为去除此种趋势影响和避免异方差问题，可对其进行对数处理。

（二）湖南省人均GDP模型的建立

走势图反映出对数化的人均GDP随时间变化呈明显规律性，设置如下两种模型对原时间序列进行拟合，用Eviews软件进行回归得到：

从上述两个模型的DW值可以看出两个模型的残差项均存在序列相关性，此时不能采用传统最小二乘法进行估计，可以采用混合时序模型，用ARMA模型拟合残差项，来消除残差项序列相关性的负面影响。在用ARMA模型进行拟合残差项前要保证该序列为平稳序列。若序列不平稳，则要对该序列进行差分，再拟合。本文用ADF检验残差序列的平稳性。

结果显示均通过了检验，所以继续用ARMA（p，q）模型对残差序列进行拟合。在拟合中要依据其自相关函数与偏自相关函数选择p与q的具体值，并根据SIC准则，进行ARMA最优模型选择。将最优模型分别与模型一、二结合，最后得到人均GDP混合时序模型分别为：

模型一对应的最终混合时序模型为：

模型二对应的最终混合时序模型为：

第三个模型的t检验与F检验均符合条件，但模型四的t2系数较为不显著。通过拟合效果图得出混合时序模型都较好的反映了真实序列的相关信息。

（三）模型检验

（1）参数显著性检验：相关结果表明模型三通过了显著性检验，模型四的t2系数不显著，但整体系数显著。（2）系数整体显著性检验：相关结果表明均通过了F检验。（3）相关性检验：在模型三和四中DW值都大约为2，代表残差项不存在一阶自相关性。然后继续进行LM检验，得出两个模型的残差序列不存在多阶序列相关性。

综上所述，模型三、四均通过了模型检验，我们用其对已知的2013年湖南省人均GDP值进行预测，后将预测值与真实值对比，来选择最优的模型对其拟合。2013年湖南省人均GDP真值为36763元，用模型三进行预测结果为38376元，相差1613元，用模型四进行预测结果为35513元，相差1250元。可以明显看出模型四预测精度较高，所以选模型四拟合该序列。

（四）预测2014年湖南省人均GDP数值

通常构建模型中使用的数据较少，且时间序列反映的为短期变化情况，因此只适合进行短期预测，在此我们只预测2014年数值。进行短期预测时选择模型四的形式，用已知的1978-2013年的湖南省人均GDP值对未知的2014年人均GDP值进行预测。经计算得2014年湖南省人均GDP的值为38445元。今后每经过一年就可以得到一个新的实际数据，即增加一个样本观测值，按上述方法重新拟合，后再用新的模型对后续几年预测，以此得到较高精度。

四、结语

本文用时间序列混合模型对湖南省人均GDP值进行拟合。经研究得出模型四较好的拟合了湖南省人均GDP值，预测精度较高。并随样本数据的增加，会不断对模型进行修正，使模型预测精度逐渐提高，因此可以认为该模型较好的反映了湖南省经济发展状况。

［1］成刚，袁佩琦，陈瑾.北京市人均GDP的时间序列分析及预测［J］.生产力研究，2007.

［2］严天艳，吕王勇，朱丽萍.中国人均GDP的时间序列模型的建立与分析［J］.西安民族大学学报（自然科学版），2008，6（34）.

［3］祝丹.福建省人均GDP预测模型及其应用［J］.漳州师范学院学报（哲学社会科学版），2008，68（2）.

（作者单位：湖南科技大学商学院）