基于铣刀精确建模的刀尖点频响函数预测方法

朱坚民， 何丹丹， 张统超



基于铣刀精确建模的刀尖点频响函数预测方法

朱坚民， 何丹丹， 张统超

(上海理工大学 机械工程学院，上海200093)

为准确地获取铣刀刀尖点频响函数，提出一种基于铣刀精确建模的刀尖点频响函数的预测方法。该方法基于RCSA理论和Timoshenko梁理论，将机床-主轴-刀柄-刀具系统划分为机床-主轴-刀柄-部分刀杆和剩余铣刀两个部分，并将剩余铣刀细分为剩余刀杆、过渡段以及多段刀齿。将铣刀分为对称型铣刀和非对称型铣刀两类，并针对每类铣刀各部分分别进行精确建模。以多把2刃和4刃铣刀为研究对象，进行实验测试，比较本文方法、等效质量法预测的铣刀刀尖点频响函数与实测刀尖点频响函数之间的差异，分析结果表明：该方法比等效质量法具有更高的预测精度，所预测频响函数的固有频率与实测频响函数固有频率的相对误差在5%以内。

刀尖点频响函数预测；响应耦合子结构分析法；等效质量法；铣刀精确建模；实验模态测试

机床高速加工过程中，机床的切削颤振会降低工件表面精度，甚至会加剧刀具的磨损和主轴的损坏[1]。目前，避免机床切削颤振最为有效的方法是借助颤振稳定性叶瓣图来确定避开引起机床颤振的切削工艺参数[2]，而获得切削系统刀尖点频响函数是确定颤振稳定性叶瓣图的先决条件。刀尖点的频响函数可以通过模态锤击实验获得，但在实际加工过程中，由于刀具刀柄的不同组合所引起的重复性模态测试，不仅会占用加工的大量时间，还会引入人为误差[3]。为此，SCHMITZ等[4]提出了响应耦合子结构分析(Receptance Coupling Substructure Analysis，RCSA)法用于预测铣刀刀尖点频响函数，将该方法应用到HSK[5]刀柄上，采用多把长径比不同的刀具进一步验证了RCSA理论的正确性，并将此法用于预测稳定性叶瓣图[6]。为了获得更为准确的铣刀刀尖点频响函数，近年来，很多学者在此基础上对该方法进行了改进，主要在结合面建模及参数识别[7-13]等方面进行了诸多研究，如王二化等[7]利用传递矩阵法与RCSA耦合算法预测刀尖频响函数，并通过PSO优化算法辨识主轴-刀柄、刀柄-刀具的结合面参数。AHMADI等[8]建立主轴-刀柄-刀具结合面刚度的多项式模型，并通过非线性最小二乘法辨识方程参数，基于RCSA法预测铣刀刀尖点频响函数。MEHRPOUYA等[9]采用逆响应耦合法辨识组合刀具中刀具子结构之间的结合面参数。AHMADIA等[10]采用连续弹性层模拟主轴-刀柄、刀柄-刀具的结合面，推导出包含结合面的系统频响函数公式。SCHMITZ等[11]提出多点响应耦合法建立刀柄-刀具结合面的模型，并耦合到机床主轴系统中[12]，预测铣刀刀尖点频响函数。XIAO等[13]通过有限元法建立主轴-刀柄之间无质量、无厚度的结合面模型，通过系统的振动方程辨识结合面参数，并在有限元中预测刀柄末端的频响函数。但是基于铣刀精确建模的研究并不多，而铣刀的精确建模对于刀尖点频响函数的准确预测也具有重要影响[14]。目前铣刀的建模方法主要是等效建模法，即将铣刀划分为刀杆和刀齿两个部分，通过不同的等效原则将刀齿部分等效为均匀直径圆柱梁。张俊等[14]总结了铣刀等效建模的三种方法，即等效质量法(Equivalent Mass Method，EqM法)、等截面积法以及等刚度法，并提出了基于等平均惯性矩法进行修正的铣刀刀齿等效建模方法[15]，该方法考虑了铣刀刀齿占总长的比例、刀齿螺旋角以及刀具长径比等因素。ZHANG等[16]还在铣刀等效直径的计算上采用刀齿质量等效的方法，通过对比预测刀尖点频响函数和实测刀尖点频响函数，表明等效质量法的等效效果较好。KOPS等[17]建立了3刃和4刃铣刀刀齿截面的实际模型，利用刀齿刚度相等的原则计算刀齿等效直径，对于所测试的3刃铣刀和4刃铣刀，其等效模型和实际模型的受力变形误差大约在2.25%。此外，FILIZ等[18-19]不区分铣刀的刀杆和刀齿，直接采用与铣刀最外端的包络圆直径相等的圆柱体进行等效建模。

上述研究中，将铣刀采用不同原则等效为等直径梁无法精确反映铣刀的真实结构，未考虑铣刀的真实曲面，进而导致刀尖点频响函数的预测精度有待进一步提升。针对以上问题，本文提出铣刀精确化建模 (Actual Modeling of Milling Cutter，AMMC)的方法，该方法按铣刀的实际结构将铣刀细分为铣刀刀杆、过渡段以及多段刀齿，分别进行精确建模。并基于RCSA理论和Timoshenko梁理论，对铣刀刀尖点的频响函数进行预测，获得了较高的预测精度。

1　机床-主轴-刀柄-刀具系统的响应耦合模型

1.1机床-主轴-刀柄-刀具系统的子结构划分

为提高刀尖点频响函数的预测精度，本文对铣刀进行精确建模，将机床-主轴-刀柄-刀具系统划分为机床-主轴-刀柄-部分刀杆和剩余铣刀两大部分。考虑铣刀的实际结构，将剩余铣刀细分为剩余刀杆、过渡段以及多段刀齿。图1以立式加工中心VMC850E的加工系统为例，给出了系统子结构划分的示意图。图1中，机床-主轴-刀柄-刀具系统被划分为7个子结构，其中子结构Ⅰ-Ⅳ为刀齿部分，子结构Ⅴ为铣刀过渡段，子结构Ⅵ为剩余刀杆，子结构Ⅶ为机床-主轴-刀柄-部分刀杆部分。

图1　机床-主轴-刀柄-刀具系统的子结构划分Fig.1 Substructure division of machine tool-spindle-holder-cutting tool system

1.2机床-主轴-刀柄-刀具系统的子结构响应耦合分析

假设子结构Ⅰ-Ⅶ之间为刚性耦合，通过RCSA顺序耦合各子结构Ⅰ-Ⅶ确定刀尖点的原点频响函数矩阵。下面以图1中子结构Ⅰ、Ⅱ的耦合为例说明RCSA原理。将子结构Ⅰ和子结构Ⅱ耦合后两端自由的子结构记为Ⅰ-Ⅱ，耦合原理如图2所示。

图2　RCSA耦合子结构Ⅰ、Ⅱ的原理Fig.2 Principle of RCSA used to couple substructure Ⅰ and Ⅱ

图2中两端自由的子结构Ⅰ、Ⅱ的频响函数矩阵Rij可表示为通式(1)

(1)

式中:i,j=1,2a或i,j=2b,3a，Hij、Lij、Nij和Pij依次为子结构Ⅰ或子结构Ⅱ在j点激励下i点获得响应的位移/力、位移/力矩、转角/力以及转角/力矩的频响函数。Fj、Mj分别为j点处所受到的外力和外力矩；Xi、θi分别为在外力和外力矩的作用下i点处的平动位移和转角。

耦合后的子结构Ⅰ-Ⅱ的频响函数矩阵RCij可表示为通式(2)

(2)

式中:RCij为子结构Ⅰ-Ⅱ的频响函数矩阵(i,j=1,3a)，HCij、LCij、NCij和PCij依次为子结构Ⅰ-Ⅱ在j点激励下i点获得响应的位移/力、位移/力矩、转角/力以及转角/力矩的频响函数。

根据子结构Ⅰ和子结构Ⅱ在结合处的兼容条件和平衡方程，可得到子结构Ⅰ-Ⅱ的频响函数矩阵与子结构Ⅰ、子结构Ⅱ的频响函数矩阵之间的关系，如式(3)所示[20]。

(3)

类似地，根据RCSA理论，通过式(3)顺序耦合子结构Ⅰ-Ⅶ，最终得到刀尖点原点频响函数矩阵G11。

G11=RC11-RC17a(RC7a7a+R7b7b)-1RC7a1

(4)

式中:G11可表示为

(5)

式中：HC11、LC11、NC11和PC11依次为刀尖点的位移/力、位移/力矩、转角/力以及转角/力矩的频响函数，其中HC11也可简称为刀尖点频响函数。

为借助颤振稳定性叶瓣图来确定不会引起机床颤振的切削工艺参数，需根据刀尖点频响函数计算铣刀极限切削宽度blim，如式(6)所示，并通过比较实际切削宽度是否小于极限切削宽度blim以判断铣削过程的稳定性。因此刀尖点频响函数的准确性对于blim计算结果的可靠性具有至关重要的作用。

(6)

式中：Kf为切削厚度方向上的切削力系数；m为在切削的平均齿数；Re(H(ω))为铣刀刀尖点频响函数的实部。

另外，式(4)中的R7b7b是子结构Ⅶ末端的频响函数矩阵，可表示为

(7)

式中:H7b7b可通过对子结构Ⅶ进行锤击试验得到。由于R7b7b中考虑了与转动自由度相关的频响函数L7b7b、N7b7b和P7b7b，而转角无法直接准确测量，导致与转动自由度相关的频响函数难以求解，一般采用间接计算方法。目前学者提出的间接计算方法主要有解方程组法[19]，一阶有限差分法[21]，二阶有限差分法[22-23]，多段EB梁公式法[24]。和其他方法相比，一阶有限差分法应用广泛、测量简便，本文基于RCSA理论，采用一阶有限差分法计算R7b7b中的L7b7b、N7b7b和P7b7b，原理如图3所示。

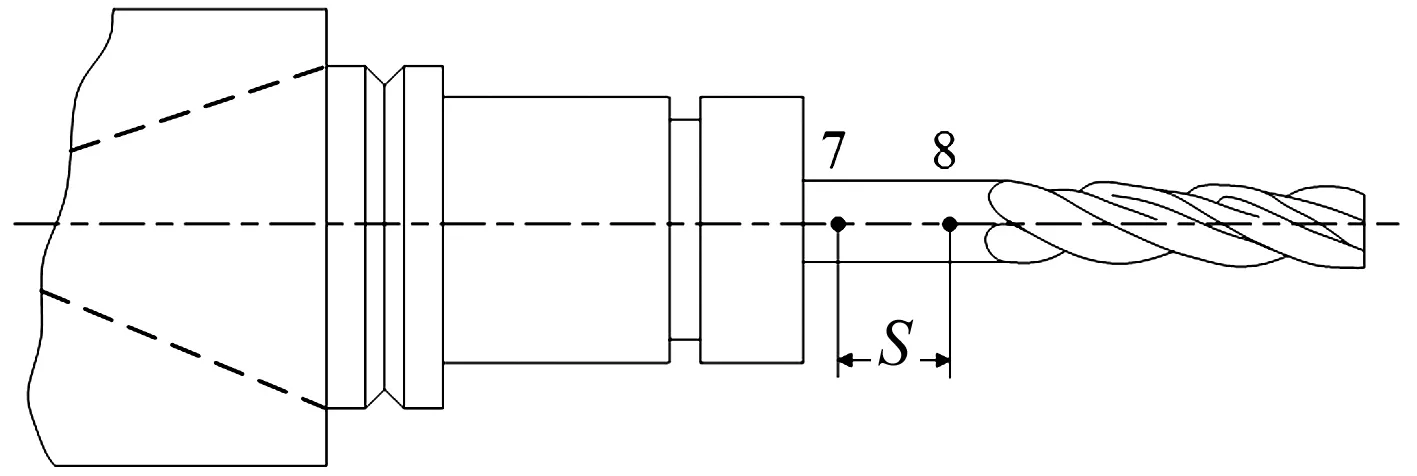
图3　有限差分法计算原理图Fig.3 Principle of finite difference method

首先通过一阶有限差分法计算出图3中7点处的频响函数矩阵G77，然后根据RCSA的耦合原理，推导出G77的耦合公式，如式(8)所示。

G77=RC7a7a-RC7a7a(RC7a7a+R7b7b)-1RC7a7a

(8)

根据式(8)可反向推出R7b7b，如式(9)所示。

R7b7b=RC7a7a(RC7a7a-G77)-1RC7a7a-RC7a7a

(9)

式中:RC7a7a为子结构Ⅰ-Ⅵ耦合后的频响函数矩阵，可通过本文第2节理论计算而得。G77可表示为

(10)

式中:H77可通过锤击试验获得，其他参数可通过一阶有限差分法计算而得。根据一阶有限差分法有

(11)

式中:S为点7和点8之间的距离，H77为刀杆上点7的原点平动位移频响函数，H78为刀杆上点8的跨点平动位移频响函数，H77、H78可通过锤击试验得到。

根据频响函数矩阵的互易性原理有

N77=L77

(12)

则

(13)

至此，R7b7b中的参数均可确定，将R7b7b代入式(4)中可得到理论刀尖点原点频响函数矩阵G11，从而确定刀尖点频响函数HC11。

2　子结构Ⅰ-Ⅵ的频响函数计算

子结构Ⅰ-Ⅵ在自由状态下，其频响函数矩阵可通过有限元、EB梁模型或Timoshenko梁模型计算得到。有限元法需要建立刀具的三维模型，当处理的刀具种类较多，刀具结构复杂时，该方法相比于梁模型计算法显得费时费力。EB梁模型忽略了梁的转动惯量和剪切效应，计算简单，适用于细长梁的频响函数计算；而Timoshenko梁考虑了梁的转动惯量和剪切效应，对于短粗梁的频响函数计算相比EB梁模型更为准确。本文考虑铣刀的精确建模，将铣刀细分为多段短粗梁，如图1所示，铣刀各子结构的长径比较小，适合用Timoshenko梁模型计算其频响函数。根据文献[20,25-26]，按照Timoshenko梁模型，参照图4定义的单个两端自由的子结构，可得到其频响函数的计算公式，如式(14)～(17)所示。

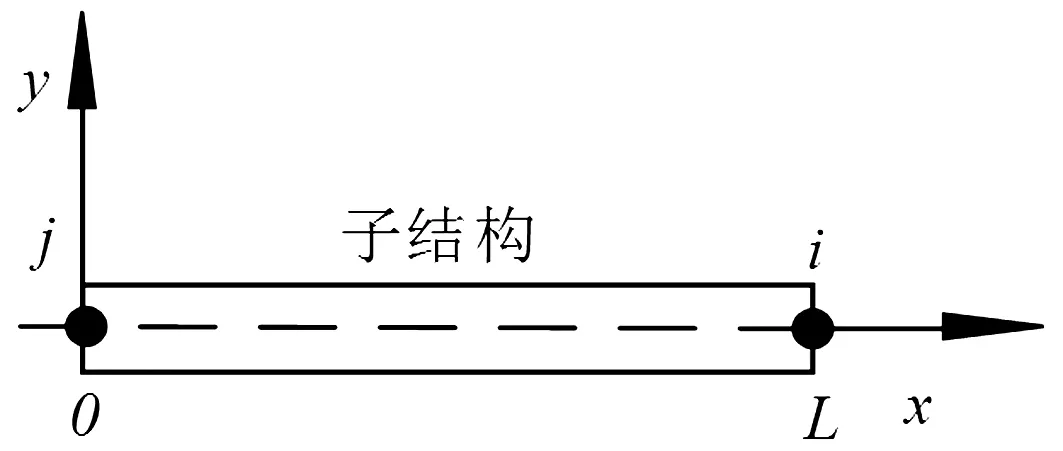
图4　两端自由的Timoshenko梁模型的坐标定义Fig.4 Coordinate definition of a free-free Timoshenko beam model

(14)

(15)

(16)

(17)

式中:Φ,Φ′分别为两端自由的Timoshenko梁的平动振型函数和平动振型函数对x的导数，且Φ是截面惯性矩的函数[20,25]；γ为阻尼因子，ω为角频率，r为模态阶数。

本文对铣刀进行精确建模，图1中子结构Ⅰ-Ⅵ的截面形状不同，如图5所示。根据式(14)～(17)，对于同一把铣刀，各子结构Ⅰ-Ⅵ的频响函数计算中除了截面惯性矩不同外，其他参数均相同，因此，子结构Ⅰ-Ⅵ的频响函数计算的差异主要在于子结构Ⅰ-Ⅵ截面惯性矩的不同。

3　子结构Ⅰ-Ⅵ截面惯性矩的计算

铣刀的建模一般忽略铣刀刀齿过渡段的实际建模，将铣刀分为刀杆和刀齿两个部分，并通过不同的等效原则将刀齿简化等效为均匀直径圆柱梁，其中EqM法计算简单，应用广泛。为了验证本文AMMC法的有效性，将通过对比AMMC法、EqM法预测的刀尖点频响函数与实测刀尖点频响函数三者之间的差异来说明。EqM法基于铣刀刀齿质量和均匀直径圆柱梁质量相等的原则，确定刀齿等效模型直径dm，如式(18)所示。

(18)

式中,M为刀具总质量；ρ为刀具材料的密度；ls、ds分别为刀杆的长度和直径；lf为铣刀刀齿段的长度。

通过对图5所示的铣刀实际结构的分析，如将铣刀截面等效为圆形截面计算其截面惯性矩会产生较大的建模误差。本文采用AMMC法按照铣刀实际截面形状计算其截面惯性矩，并将铣刀分为对称型铣刀和非对称型铣刀，即在铣刀截面建立x-y笛卡尔二维坐标系，如果铣刀刀齿截面对x轴的惯性矩和对y轴的惯性矩相等，则该铣刀属于对称型铣刀，否则属于非对称型铣刀。

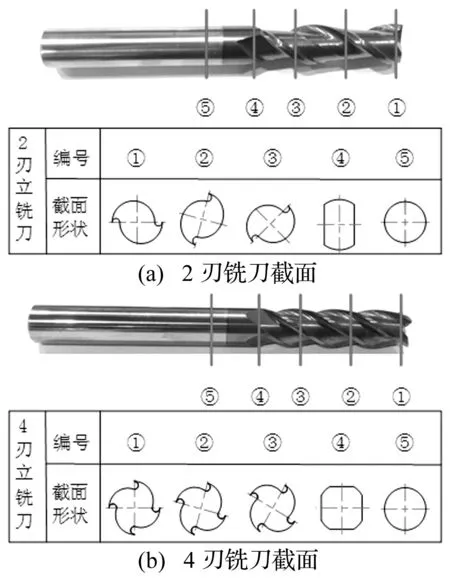
图5　2刃和4刃铣刀截面Fig.5 Section of the two fluted milling cutter and the four fluted one

本文以右旋2刃铣刀(非对称型铣刀)和右旋4刃铣刀(对称型铣刀)为例，推导基于AMMC法的对称型铣刀和非对称型铣刀各子结构截面惯性矩的计算公式，并确定相关参数。

3.1铣刀刀齿段子结构Ⅰ-Ⅳ截面惯性矩的计算

由于刀齿螺旋槽的存在，对称型铣刀和非对称型铣刀的刀齿部分具有如下特点，即在距刀齿端面不同距离处的刀齿截面几何形状相同，不同的是其位置相对刀齿端面转动了一个角度，如图6所示。令u-v为铣刀刀齿任意截面上的坐标系，x-y为铣刀刀齿端面的坐标系，u-v相对于x-y的转角为ψ。为计算方便，将u-v作为铣刀刀齿任意截面上的局部坐标系，将x-y作为铣刀各部分截面惯性矩计算的全局坐标系，并将刀齿任意截面u-v坐标系下的截面惯性矩转换到x-y坐标系下，转换过程如式(19)所示。因此，本文首先计算铣刀端面处的截面惯性矩，然后根据式(19)确定距离铣刀端面不同距离处的刀齿截面惯性矩。

(a)　2刃铣刀刀齿端(截)面坐标系定义

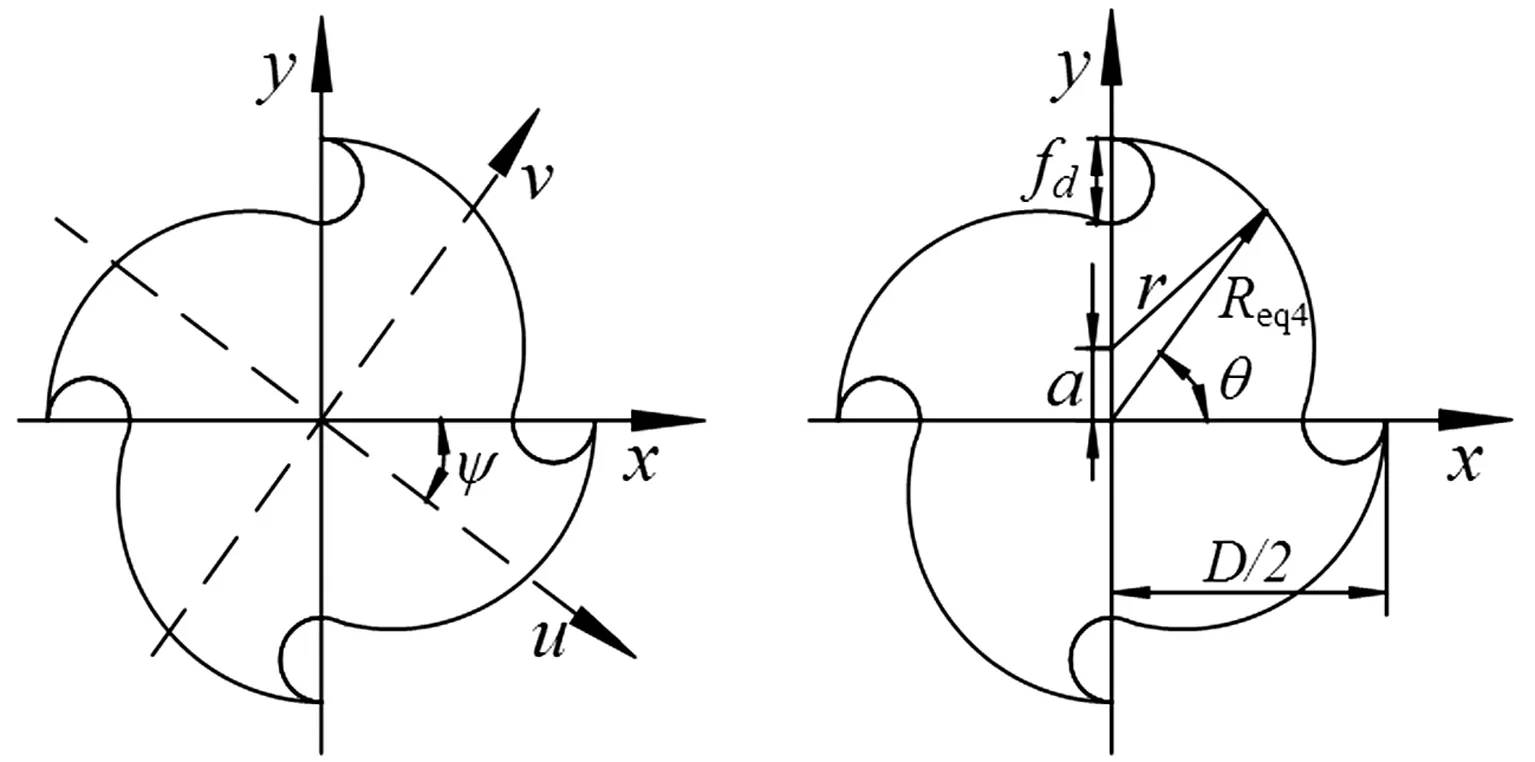
(b)　4刃铣刀 刀齿端(截)面坐标系定义图6　2刃铣刀和4刃铣刀刀齿端(截)面坐标系Fig.6 Coordinate system of the two fluted milling cutter’s end face (or section) and the four fluted one’s

(19)

(20)

式中：z为铣刀刀齿任意截面距离刀齿端面的距离；β为铣刀螺旋角；D为铣刀刀齿圆柱基体直径。

由图6可以看出，2刃和4刃铣刀截面具有中心对称的特点。根据文献[1]，可先求解1/2的2刃铣刀和1/4的4刃铣刀端面的惯性矩，如式(21)、式(22)所示。

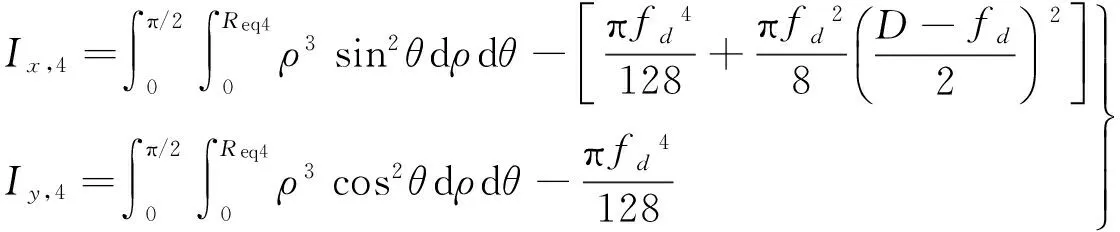
式(21)、(22)中，

(23)

(24)

式(23)、(24)中，r为铣刀切削刃圆弧半径，a为铣刀切削刃圆弧中心到铣刀中心的距离，fd为铣刀螺旋槽直径。Reqi为i刃铣刀刀齿截面的等效半径，i=2,4。Ix,j为j刃铣刀刀齿端面对x轴的惯性矩，Iy,j为j刃铣刀刀齿端面对y轴的惯性矩，j=2,4。

将式(23)代入式(21)，得到2刃铣刀刀齿端面对x轴的惯性矩和对y轴的惯性矩，如式(25)所示。由于Ix,2、Iy,2展开式较为复杂，本文通过中间量I21、I22、I23和矩阵A、B、C表示，I21、I22、I23的定义如式(26)所示，A、B、C的定义如式(27)所示。

(25)

(27)

将式(24)代入式(22)，得到4刃铣刀刀齿端面对x轴的惯性矩和对y轴的惯性矩，如式(28)所示。同理，Ix,4、Iy,4可通过中间量I41、I42、I43和矩阵D、E、F表示，I41、I42、I43的定义如式(29)所示，D、E、F的定义如式(30)所示。

(28)

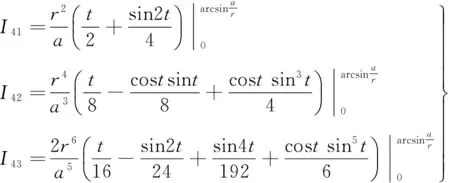
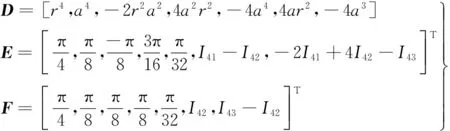
然后根据刀齿截面中心对称的特点可得到2刃铣刀和4刃铣刀刀齿端面剩余部分的截面惯性矩，最后通过叠加原理得到2刃和4刃铣刀刀齿端面对x轴总的惯性矩Ix,2tot、Ix,4tot和对y轴总的惯性矩Iy,2tot、Iy,4tot，如式(31)和式(32)所示。

(31)

(32)

式(23)、(24)中，r,a可通过铣刀刀齿端面的几何边界条件确定。对于2刃铣刀，其几何边界条件如式(33)所示，通过求解得到r,a，如式(34)所示。

(33)

(34)

同理可得4刃铣刀刀齿的参数r,a，如式(35)所示。

(35)

为了获得铣刀刀齿部分距刀齿端面不同距离处的截面惯性矩，可将求出的Ix,2tot和Iy,2tot、Ix,4tot和Iy,4tot代入式(19)，即可得到2刃和4刃铣刀刀齿部分距刀齿端面不同距离处的截面惯性矩。

3.2铣刀过渡段子结构Ⅴ截面惯性矩的计算

铣刀刀齿和刀杆之间的部分为铣刀过渡段，2刃和4刃铣刀过渡段的截面形状如图7所示。

图7　2刃铣刀和4刃铣刀过渡段截面分块Fig.7 Transition section block of the two fluted milling cutter and the four fluted one

本文对铣刀过渡段截面惯性矩的计算采用分块计算再叠加的方法。根据对称型铣刀和非对称型铣刀截面的特点，在铣刀过渡段截面建立以其形心为坐标原点的笛卡尔二维坐标系，然后以其原点为中心，划分出若干块三角形区域和扇形区域，分别计算每块区域的截面惯性矩后再依次叠加，确定截面整体的截面惯性矩。下面以2刃铣刀为例具体说明计算过程。

步骤1以2刃铣刀过渡段截面形心为坐标原点，建立笛卡尔二维坐标系，如图7(a)所示。

步骤2将2刃铣刀划分为四个区域，分别标号为①、②、③、④。

步骤3分别计算各区域对x轴的惯性矩和对y轴的惯性矩。

步骤4叠加各区域对x轴的惯性矩和对y轴的惯性矩，最终得到整个截面对x轴总的惯性矩和对y轴总的惯性矩。

图7(a)中，②、④为三角形区域，①、③为扇形区域，先按照图8(a)、8(b)分别建立坐标系计算单个三角形区域和扇形区域对x轴惯性矩和对y轴惯性矩，如式(36)所示。

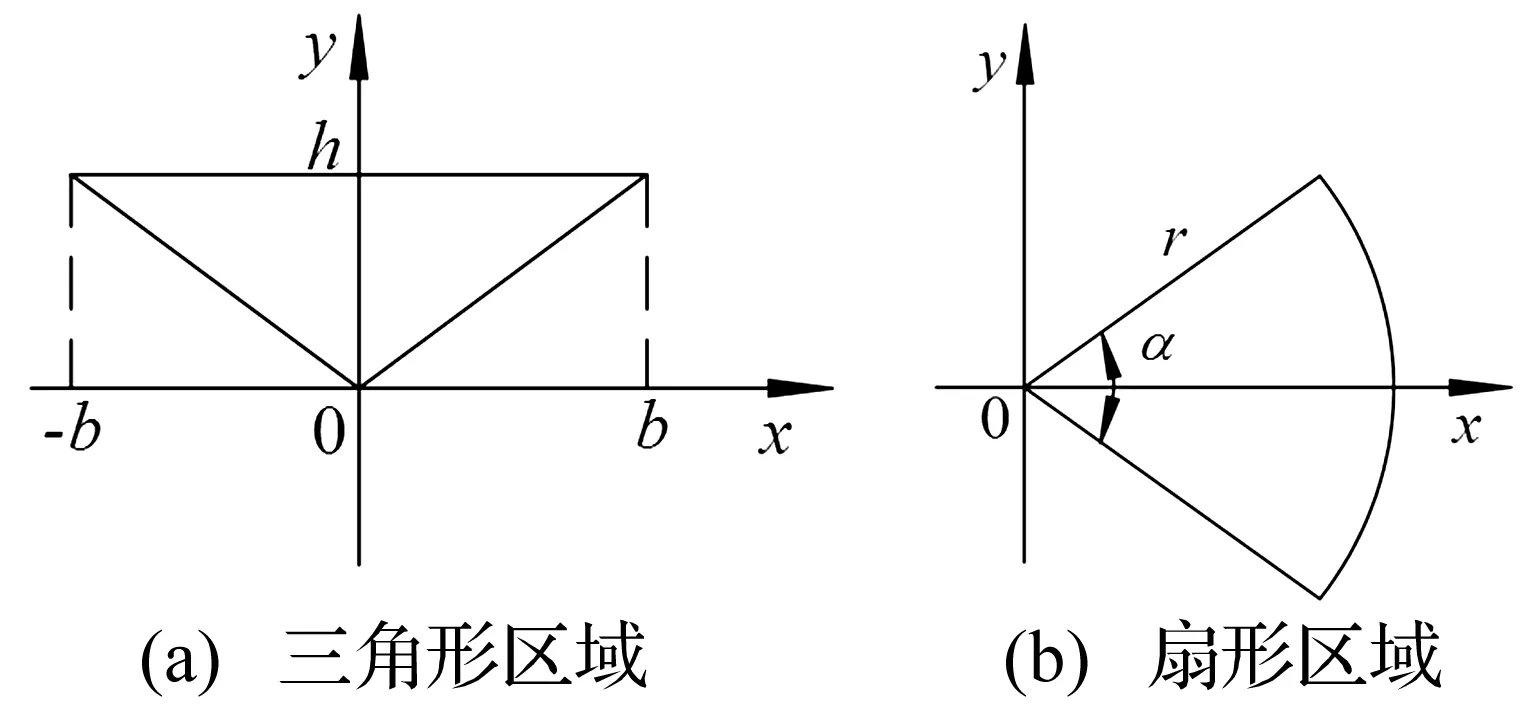
图8　三角形、扇形截面坐标系Fig.8 Coordinate system of triangle and sector cross section

(36)

式中:Itx为三角形截面对x轴的惯性矩；Ity为三角形截面对y轴的惯性矩；Isx为扇形截面对x轴的惯性矩；Isy为扇形截面对y轴的惯性矩。

然后根据坐标转换原理得到剩余部分三角形区域和扇形区域的截面惯性矩，转换原理同式(19)。经过叠加，最终得到2刃铣刀过渡段截面对x轴总的惯性矩Ix,2tot和对y轴总的惯性矩Iy,2tot，如式(37)所示。

(37)

同理可得4刃铣刀过渡段对x轴总的惯性矩Ix,4tot和对y轴总的惯性矩Iy,4tot，如式(38)所示。

(38)

3.3铣刀刀杆子结构Ⅵ截面惯性矩的计算

铣刀刀杆部分截面为圆形，其对x轴的惯性矩Ix和对y轴的惯性矩Iy为

(39)

式中:D为铣刀刀杆段的直径。

4　实验研究

4.1实验方案与步骤

为验证本文AMMC法的有效性，本文在VMC850E立式加工中心上进行实验研究。

根据AMMC法的理论推导可知，2刃铣刀x向、y向上的理论刀尖点频响函数不同，4刃铣刀x向、y向上的理论刀尖点频响函数相同。根据式(6)计算铣刀的极限切削宽度blim时，2刃铣刀会因为x向、y向上刀尖点频响函数的差异，而需判断采用哪个方向的频响函数计算blim更为可靠。因此本文先通过实验验证AMMC法将铣刀分为对称型和非对称型铣刀分别进行建模的合理性和必要性，即通过实验测试结果判断2刃和4刃铣刀各自在x向、y方向上的刀尖点频响函数是否存在差异，并讨论2刃铣刀采用哪个方向上的频响函数计算blim更为可靠。然后通过对比AMMC法铣刀建模、EqM法铣刀建模时预测的刀尖点频响函数与实测刀尖点频响函数之间的差异，验证AMMC法的有效性。实验中所用的主要设备和铣刀的相关参数如表1和表2所示。

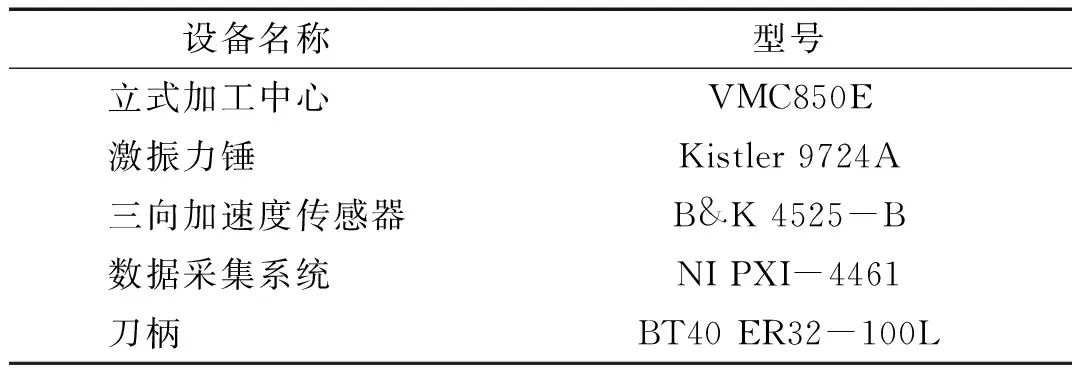
表1　实验设备相关参数

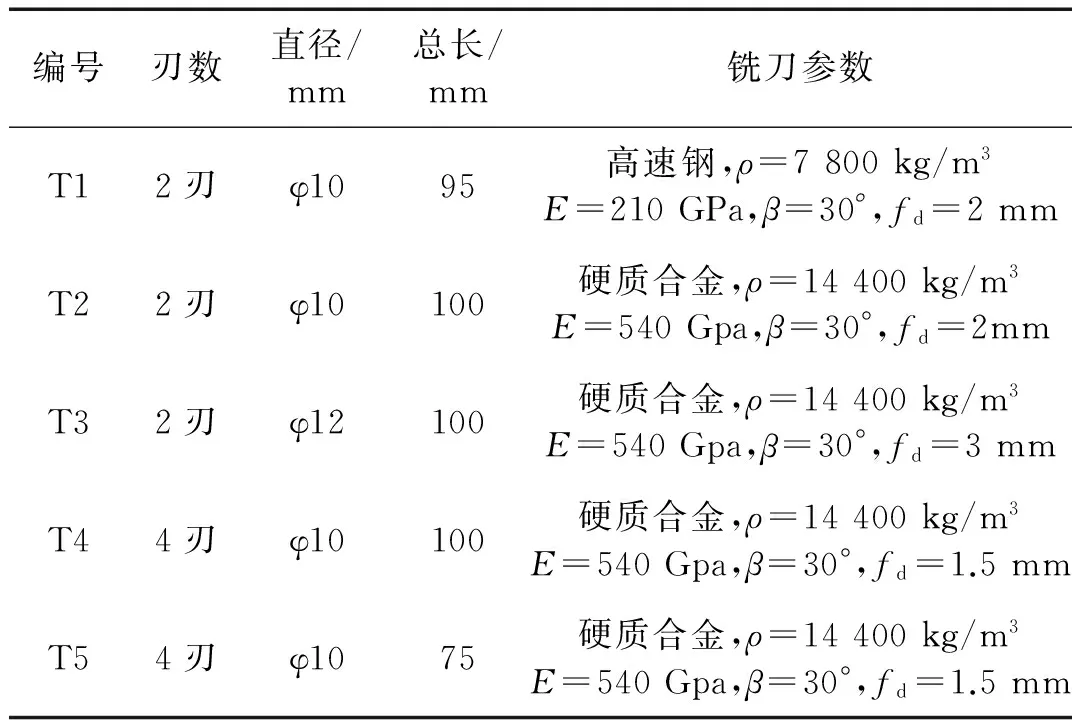
表2　实验所用铣刀参数表

实验步骤如下：

步骤1按照图9所示原理安装铣刀和加速度传感器，进行刀尖点频响函数测试。实验所用铣刀在刀柄中的装夹长度均为20 mm，分别测量2刃和4刃铣刀x向、y向的刀尖点频响函数。

图9　铣刀刀尖点频响特性测试Fig.9 Tool point frequency response test

步骤2按照图10(a)所示原理搭建实验平台，按照图10(b)安装加速度传感器。选择铣刀刀杆上点7的位置，该点位置的选择需要注意两点：①便于力锤进行锤击实验；②尽可能地接近刀柄末端，如果点7 距离刀柄太远会影响S的取值。

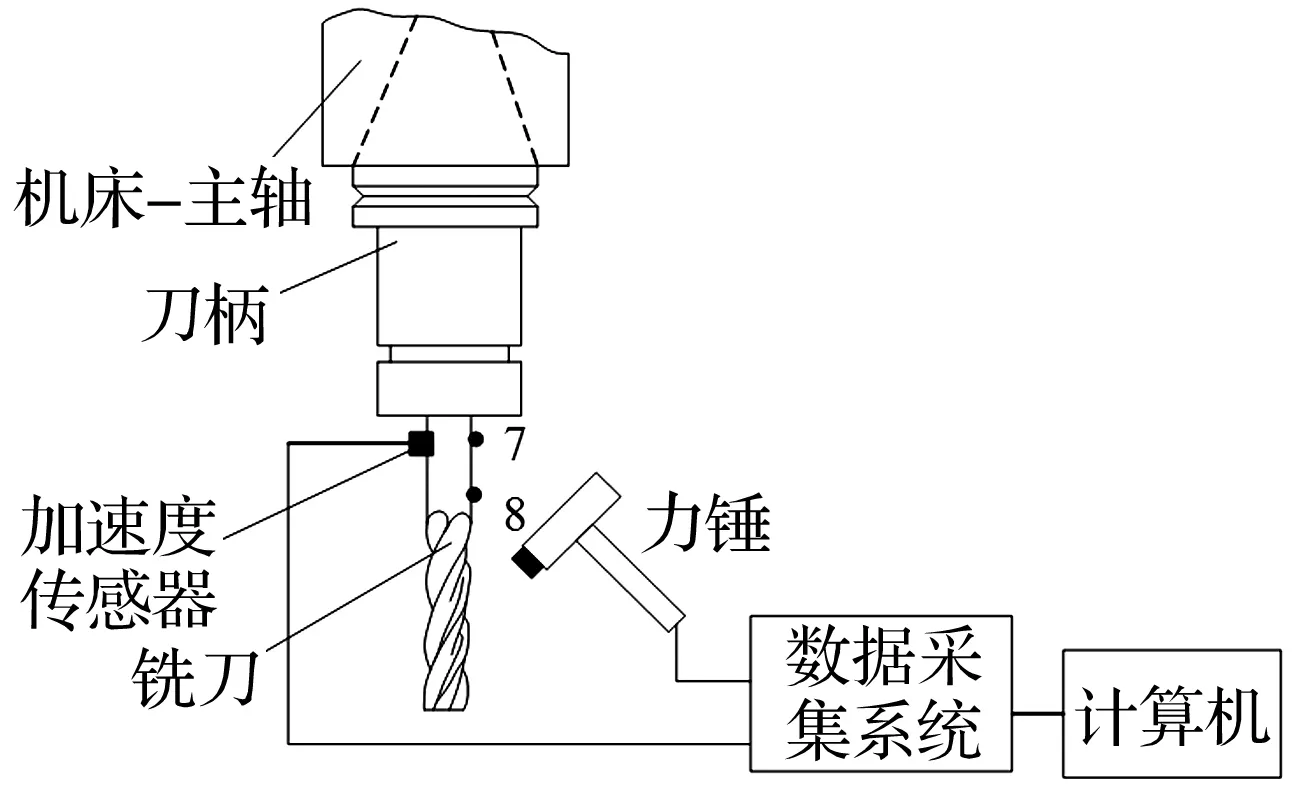
(a)　H77和H78锤击试验测量的实验原理图

(b)　H77和H78锤击试验测量的实际实验照片图10　H77和H78锤击试验测量的实验原理图和实验照片Fig.10 Experiment principle and test diagram of measuring H77 and H78

步骤3：选择点8的位置，点8与点7之间的距离为S，两者位于同一条母线上，以保证锤击力的方向和传感器测量的加速度方向一致；选择点8时应注意：点8和点7之间的距离S应尽可能地选择较大的值，以保证H77和H78的差异明显，而具体的值应根据不同铣刀的参数灵活选择。本实验中S的取值如表3所示。

表3　S的取值

步骤4在点7和点8处分别进行模态锤击实验，使用力锤分别对点7和点8施加激振力，并用安装在铣刀刀杆处与点7正对的加速度传感器记录振动加速度响应，利用数据采集系统同步采集激振力信号和加速度信号，并进行多次测量，使用ModelVIEW模态分析软件对信号进行处理，得到频响函数H77和H78。

4.2实验结果与分析

根据步骤1得到实验所用铣刀x向、y向的实测刀尖点频响函数，如图11所示。

图11　不同铣刀x向、y向的实测刀尖点频响函数对比Fig.11 Comparison of different milling cutters’ experimentally obtained tool point frequency response function in x and y direction

从图11可以看出，2刃铣刀(T1、T2、T3)x向、y向的刀尖点频响函数实部之间、虚部之间均不重合，而4刃铣刀(T4、T5)x向、y向的刀尖点频响函数实部之间、虚部之间十分接近，说明2刃铣刀x向、y向的刀尖点频响函数并不相同，4刃铣刀x向、y向的刀尖点频响函数近似相等。实验结果验证了前述理论分析的正确性，同时也表明采用AMMC法将铣刀分为对称型铣刀和非对称型铣刀分别进行精确建模的必要性和合理性。从图11(a)～11(c)中还可以看出，2刃铣刀刀尖点频响函数在y向上的固有频率稍小于x向上的固有频率，y向上的频响函数实部的最小值小于x向上频响函数实部的最小值。按式(6)进行铣刀极限切削宽度blim计算时，为保证blim对于铣刀截面各个方向的适用性，式(6)中Re(H(ω))需取绝对值最大的值。即对于2刃铣刀，应选择y方向上的频响函数计算极限切削宽度；而对于4刃铣刀，可选择任意坐标方向上的刀尖点频响函数计算其极限切削宽度。为验证AMMC法的有效性，本文将AMMC法、EqM法预测的铣刀刀尖点频响函数以及实测刀尖点频响函数三者之间进行比较。根据步骤2～4得到的频响函数H77和H78，结合式(9)～(13)计算得到R7b7b，按照AMMC法和EqM法计算两种方法下各子结构的截面惯性矩，利用RCSA原理耦合各子结构，最终得到基于AMMC法、EqM法预测的铣刀刀尖点频响函数与实测刀尖点频响函数三者之间的对比，如图12所示。

图12(a)～(e)分别给出了不同刀具参数(材料、直径、长度以及刃数)下铣刀刀尖点的实测频响函数与AMMC法、EqM法建模预测的刀尖点频响函数的对比。从图12(a)～(e)可以看出：①AMMC法建模预测的刀尖点频响函数和实测的刀尖点频响函数十分接近，AMMC法建模预测的频响函数实部和虚部的幅值虽然与实测结果有一定的差异，但是AMMC法建模预测的频响函数固有频率和实测频响函数固有频率更为接近；②EqM法建模预测的铣刀刀尖点频响函数与相应的实测结果有较大偏差；③EqM法建模预测的频响函数基本上只有一阶固有频率与实测结果较为接近。从上述比较结果可看出，与EqM法相比，AMMC法能有效提高刀尖点频响函数的预测精度。

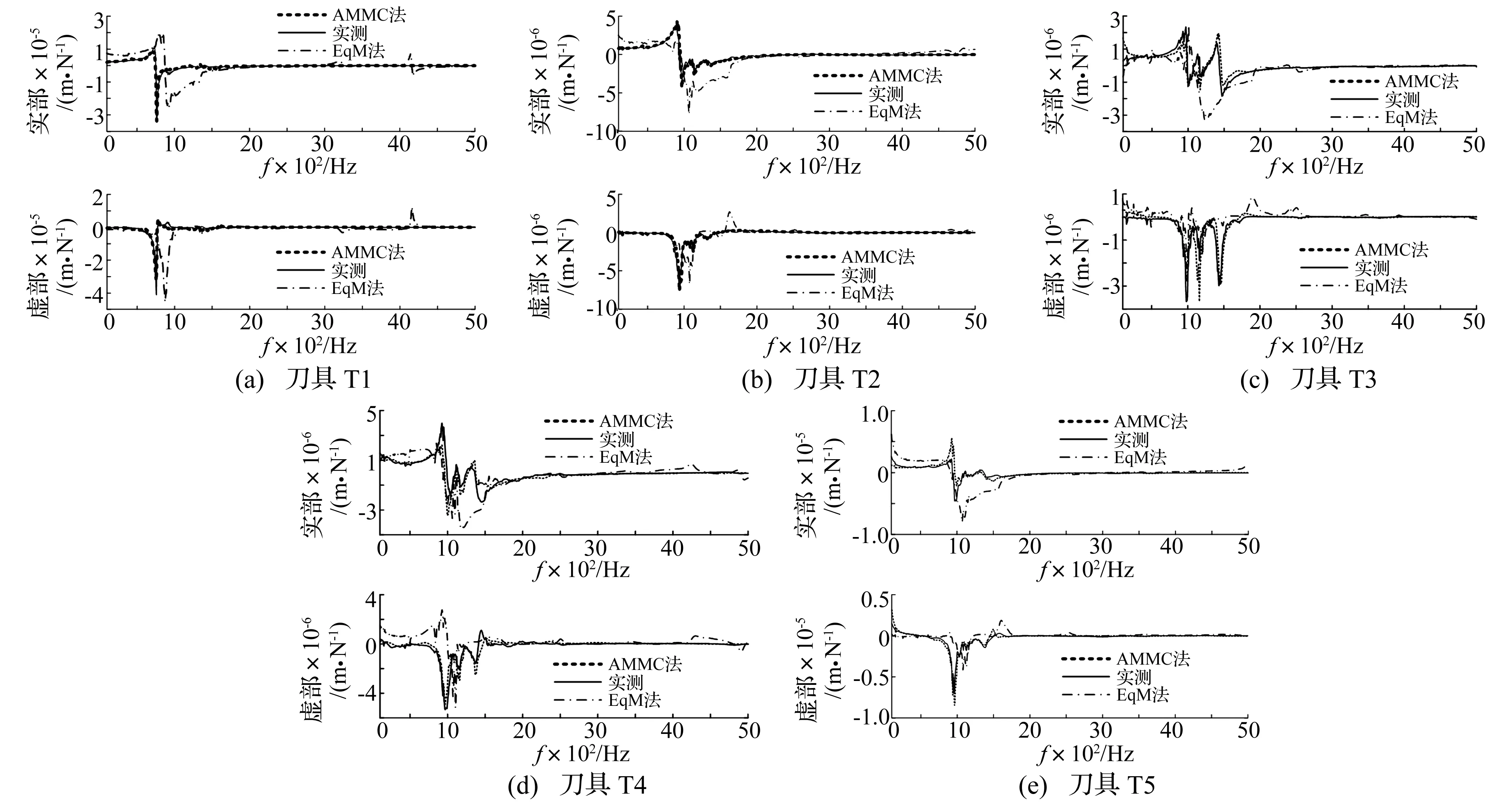
图12　两种建模方法下不同铣刀刀尖点频响函数的预测与实测结果对比Fig.12 Comparison of different milling cutters’ predicted tool point frequency response function under AMMC method and EqM method with experimental results

为了进一步量化三者之间的差异，本文对比2刃铣刀和4刃铣刀实测刀尖点频响函数、AMMC法和EqM法建模预测的刀尖点频响函数的固有频率。实验结果中，T1铣刀的实测刀尖点频响函数只有一阶固有频率最为明显，而其他铣刀实测刀尖点频响函数的前三阶固有频率比较明显，故对T1铣刀，只比较两种方法预测的频响函数的一阶固有频率与实测一阶固有频率之间的差异，对其他铣刀则比较其前三阶固有频率与实测固有频率之间的差异，如表4所示。

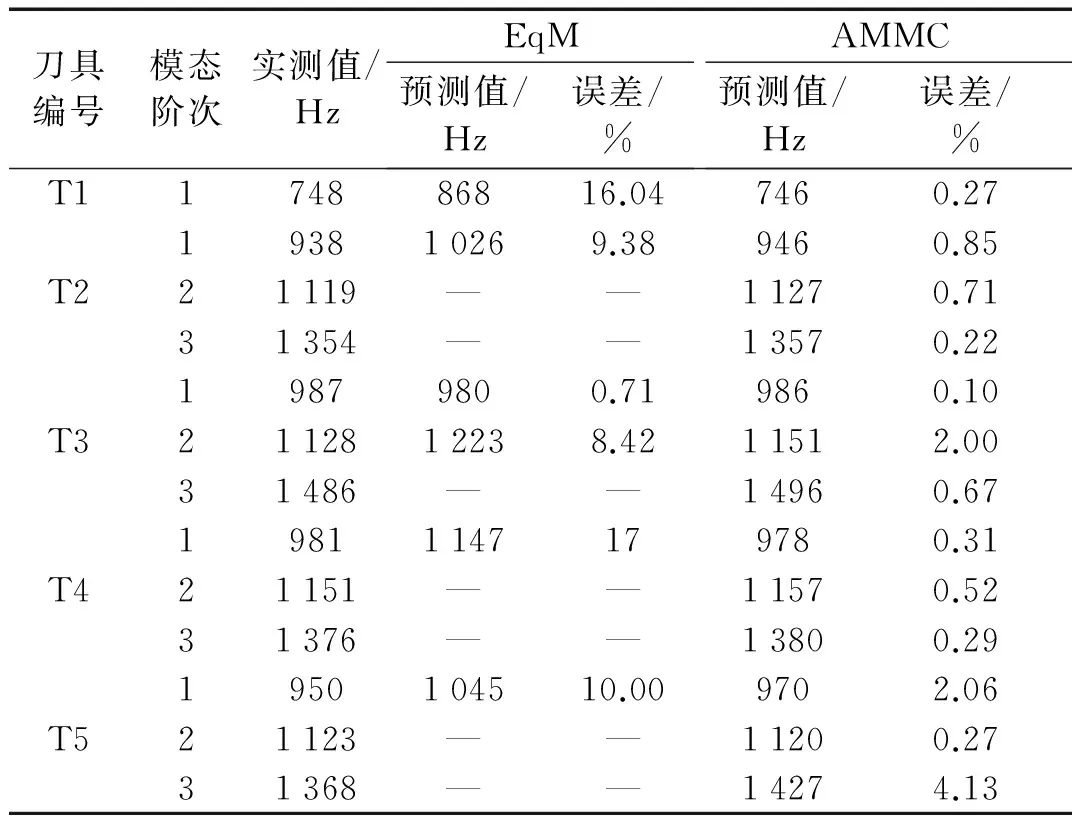
表4　两种方法下刀尖点频响函数固有频率与实测结果的对比

从表4可看出：EqM法预测的刀尖点频响函数的固有频率和实测结果之间的相对误差在0.71%～17%之间；而AMMC法预测的刀尖点频响函数的固有频率和实测结果的相对误差在5%以内，说明采用AMMC法进行铣刀建模预测的结果具有更高的精度，且从已有的实验结果可以看出：AMMC法建模对不同刀具参数(材料、直径、长度以及刃数)的刀尖点频响函数预测具有更高的预测精度。

5　结　论

(1) 提出了一种基于铣刀精确建模的刀尖点频响函数的预测方法。该方法按铣刀的实际结构精确建模，并基于RCSA方法和Timoshenko梁模型实现了刀尖点频响函数的精确预测。

(2) AMMC法建模将铣刀分为刀杆、过渡段以及多段刀齿，针对其各部分实际结构，按对称型和非对成型铣刀分别计算其截面惯性矩，有效保证了刀尖点频响函数的预测精度。

(3) 理论分析和实验结果表明：本文方法是正确的、有效的，对铣刀进行分类和精确建模是必要的，与经典的EqM法相比，本文方法具有更高的预测精度，并对预测不同参数铣刀的刀尖点频响函数具有一定的指导意义。

[1] KIVANC E B, BUDAK E. Structural modeling of end mills for form error and stability analysis [J]. International Journal of Machine Tool & Manufacture, 2004, 44: 1151-1161.

[2] 朱坚民, 王健, 张统超. 一种改进的基于响应耦合子结构法的刀尖点频响函数预测方法[J]. 中国机械工程, 2015, 26(3): 285-292.

ZHU Jianmin, WANG Jian, ZHANG Tongchao, et al. An improved tool point frequency response function prediction method based on RCSA[J]. Chinese Journal of Mechanical Engineering,2015, 26(3): 285-292.

[3] 闫蓉, 蔡飞飞, 彭芳瑜, 等. 基于响应耦合方法的铣刀刀尖点频响函数预测[J]. 华中科技大学学报:自然科学版, 2013, 41(4): 1-5.

YAN Rong, CAI Feifei, PENG Fangyu, et al. Predicting frequency response function for tool point of milling cutters using receptance coupling [J]. Huazhong University of Science & Technology:Natural Science Edition,2013,41(4): 1-5.

[4] SCHMITZ T L, DONALDSON R. Predicting high-speed machining dynamics by substructure analysis [J].Annals of the CIRP, 2000, 49(1): 303-308.

[5] SCHMITZ T L, DAVIES M A, KENNEDY M D. Tool point frequency response prediction for high-speed machining by RCSA [J]. Journal of Manufacturing Science and Engineering,2001, 123: 700-707.

[6] SCHMITZ T L, DAVIES M A, MEDICUS K, et al. Improving high-speed machining material removal rates by rapid dynamic analysis [J]. Annals of the CIRP,2001,50(1): 263-268.

[7] 王二化, 吴波, 胡友民, 等. 主轴-刀柄与刀柄-刀具结合面参数辨识研究[J]. 振动与冲击,2014,33(10):50-54.

WANG Erhua, WU Bo, HU Youmin, et al. Identification of spindle-holder and holder-tool joint parameters[J]. Journal of Vibration and Shock,2014, 33(10): 50-54.

[8] AHMADI K, AHMADIAN H. Modeling machine tool dynamic using a distributed parameter tool-holder joint interface [J]. International Journal of Machine Tools & Manufacture,2007, 47: 1916-1928.

[9] MEHRPOUYA M, GRAHAM E, PARK S S. FRF based joint dynamics modeling and identification [J]. Mechanical Systems and Signal Processing,2013, 39: 265-279.

[10] AHMADIAN H, NOURMOHAMMADI M. Tool point dynamics prediction by a three-component model utilizing distributed joint interfaces [J]. International Journal of Machine Tools & Manufacture,2010, 50: 998-1005.

[11] SCHMITZ T L, DUNCAN G S. Receptance coupling for dynamics prediction of assemblies with coincident neutral axes [J]. Journal of Sound and Vibration,2006, 289: 1045-1065.

[12] SCHITZ T L, POWELL K, WON D, et al. Shrink fit tool holder connection stiffness/damping modeling for frequency response prediction in milling [J]. International Journal of Machine Tools & Manufacture,2007, 47: 1368-1380.

[13] XIAO W W, MAO K M, ZHU M, et al. Modelling the spindle-holder taper joint in machine tools: a tapered zero-thickness finite element method [J]. Journal of Sound and Vibration,2014, 333: 5836-5850.

[14] 张俊, 黄保华, 赵万华, 等. 面向动态特性快速求解的铣刀等效模型建模方法[J]. 振动工程学报,2013, 26(3): 351-356.

ZHANG Jun, HUANG Baohua, ZHAO Wanhua, et al. The cutter equivalent model of dynamic characteristics of fast solving oriented modeling method [J]. Journal of Vibration Engineering,2013, 26(3): 351-356.

[15] 张俊, 黄保华, 赵万华, 等. 整体立铣刀动力学模型的最优等效方法[J]. 华中科技大学学报:自然科学版, 2012, 40(9): 17-20.

ZHANG Jun, HUANG Baohua, ZHAO Wanhua, et al. The optimal equivalent method of dynamics model for end mills [J]. Journal of Huazhong University of Science and Technology:Natural Science Edition, 2012, 40(9): 17-20.

[16] ZHANG J, SCHMITZ T L, ZHAO W H, et al. Receptance coupling for tool point dynamics prediction on machine tools [J]. Chinese Journal of Mechanical Engineering,2011,24(3):340-345.

[17] KOPS L, VO D T. Determination of the equivalent diameter of an end mill based on its compliance [J]. Annals of the CIRP,1990, 39(1): 93-96.

[18] FILIZ S, CHENG C H, POWELL K, et al. An improved tool-holder model for RCSA tool-point frequency response prediction [J]. Precision Engineering,2009, 33: 26-36.

[19] PARK S S, ALTINTAS Y, MOVAHHEDY M. Receptance coupling for end mills [J]. International Journal of Machine Tools & Manufacture,2003, 43: 889-896.

[20] ÖZSAHIN O, ÖZGÜVEN H N, BUDAK E. Analytical modeling of asymmetric multi-segment rotor-bearing systems with Timoshenko beam model including gyroscopic moments [J]. Computers and Structures, 2014, 144: 119-126.

[21] DUARTE M L M, EWINS D J. Rotational degrees of freedom for structural coupling analysis via finite-difference technique with residual compensation[J]. Mechanical Systems and Signal Processing, 2000, 14(2): 205-227.

[22] ALBERTELLI P, GOLETTI M, MONNO M. A new receptance coupling substructure analysis methodology to improve chatter free cutting conditions prediction[J]. International Journal of Machine Tool & Manufacture,2013,72: 16-24.

[23] SCHMIZ T L, DUNCAN G S. Three-component receptance coupling substructure analysis for tool point dynamics prediction[J]. Journal of Manufacturing Science and Engineering,2005,127:781-790.

[24] GANGULY V, SCHMIZ T L. Spindle dynamic identification using particle swarm optimization [J]. Journal of Manufacturing Processes,2013, 15: 444-451.

[25] ARISTIZABAL-OCHOA J D. Timoshenko beam-column with generalized end conditions and nonclassical modes of vibration of shear beams[J]. Journal of Engineering Mechanics,2004, 130(10): 1151-1159.

[26] 汪博, 孙伟, 闻邦椿. 基于阻抗耦合子结构法的电主轴固有特性求解[J]. 计算机集成制造系统, 2012, 18(2): 422-426.

WANG Bo, SUN Wei, WEN Bangchun. Inherent characteristic solution of motorized spindle based on receptance coupling substructure analysis [J]. Computer Integrated Manufacturing Systems,2012, 18(2): 422-426.

A prediction method for tool point frequency response function based on milling cutters’ accurate models

ZHU Jianmin， HE Dandan， ZHANG Tongchao

(School of Mechanical Engineering, University of Shanghai for Science and Technology, Shanghai 200093, China)

To obtain a more accurate tool point frequency response function, a new prediction method for tool point frequency response function based on milling cutters’ accurate models was presented. On the basis of Timoshenko beam and RCSA theories, a machine tool-spindle-holder-cutting tool system was divided into machine tool-spindle-holder-part of tool rob and the rest of milling cutter, then the rest of milling cutter was subdivided into the remaining tool rod, transition part and several cutter teeth. Furthermore, milling cutters were divided into symmetrical cutters and asymmetric cutters. The accurate models of each type of cutters were established respectively. Finally, with several two-fluted and four-fluted milling cutters as the research objects, predicted tool point frequency response function under the new method and equivalent mass method were compared with experimental results. It was experimentally proven that the new method has higher prediction accuracy than the equivalent mass method, in which the relative errors between natural frequencies of predicted frequency response function and the measured ones were within 5%.

tool point frequency response function prediction; receptance coupling substructure analysis; equivalent mass method; milling cutters’ accurate model; experimental modal testing

国家自然科学基金(50975179)；上海市教委科研创新项目(11ZZ136)；上海市科委科研计划项目(13160502500)；沪江基金(D14005)

2015-09-01修改稿收到日期：2016-01-18

朱坚民 男，博士，教授，博士生导师，1968年生

何丹丹 女，硕士生，1992年生

TH113

A

10.13465/j.cnki.jvs.2016.16.023