厦门本岛近地表三维速度结构建模研究

师黎静， 苏　茜， 刘宇实， 刘　恒

(1.中国地震局 工程力学研究所地震工程与工程振动重点实验室，哈尔滨　150080；2.武汉华阳宏创建筑设计有限公司，武汉　430000；3.南京工业大学 交通学院，南京　210009)



厦门本岛近地表三维速度结构建模研究

师黎静1， 苏茜2， 刘宇实1， 刘恒3

(1.中国地震局 工程力学研究所地震工程与工程振动重点实验室，哈尔滨150080；2.武汉华阳宏创建筑设计有限公司，武汉430000；3.南京工业大学 交通学院，南京210009)

搜集整理了厦门本岛202个钻孔资料，分析、总结了工程场地剪切波速度结构的空间相关性和带状异向性特征。在此基础上，发展了一套先通过不规则三角网(TIN)法和克里格法划分出不同土层的分界面，建立场地三维工程地质模型，再基于克里格方法对土层内部剪切波速进行空间预测，最后整合各土层剪切波速度结构的建模方法。通过建立厦门岛近地表三维速度结构模型，对方法可行性和精度进行了检验。结果表明，建立的模型，能够很好反映出厦门岛工程场地同一土层内的剪切波速变化规律及不同土层剪切波速的带状异向性。

剪切波速;三维建模;克里格法;厦门本岛

剪切波速模型是地震学和地震动研究中的基础性数据。地壳及上地幔三维速度结构建模一直是地震学领域的研究重点。刘福田等[1-4]利用强、余震记录对延怀盆地、安阳地区、京津唐、华北等地区的地壳及上地幔的三维速度结构探测和建模进行了研究。地表100 m以内浅层覆盖层虽然相对厚度小，但波速低，对地震波的整体影响要大得多。随着三维地震动模拟技术的提高，对浅层工程场地速度结构建模的研究也开始得到重视。MAGISTRALE[6-7]通过将剪切波速与地质年代以及土层深度相联系，建立了洛杉矶盆地、施甸盆地等国内外场地的三维速度结构模型。

上述研究中通常采用的思路是：利用地震波数据或钻孔数据建立波速等值面，再以等值面为控制面结合地质数据确定地质分布，最后得到三维速度结构模型。建模中以假定的剪切波速作为不同土层间划分依据，仅适用于以上百米至公里为尺度的大区域速度结构研究。

近地表覆盖层中，剪切波速随着土层类型及其空间分布的变化而变化，其变异性更加的复杂，对三维速度结构建模要求也更为精细。上述研究思路并不适用于覆盖层厚度常常在几十米范围的近地表工程场地三维波速建模研究。师黎静[8]根据唐山18个地脉动观测数据，利用地质统计学中的样条插值法与克里格插值法相结合，建立了唐山地区工程场地的三维速度结构模型。该研究主要基于地脉动方法的波速测试数据，对不同土层的划分仅基于剪切波速，也没有利用实际钻孔波速测试数据对所建立的三维速度结构模型进行检验。为了能够反映剪切波速在土层内部变化规律，需要考虑剪切波速度结构的空间相关性，更好区分不同类型土层剪切波速结构。

本文搜集整理厦门岛钻孔波速测试数据，建立场地三维工程地质模型，通过分析厦门岛滨海场地速度结构空间相关性和带状异向性特征，研究合理、高效的未知区域剪切波速空间预测方法，建立厦门岛三维近地表速度结构模型，并进行验证。

1　厦门岛近地表覆盖层及剪切波速数据

厦门岛位于福建省东南部的九龙江出海口，全岛面积约124 平方公里，地形呈现南高北低，丘陵地区集中在南部，台地及平原主要分布在北部。厦门市工程地质及搜集到的钻孔数据点分布见图1。厦门岛沉积类型主要滨海或滨岸相沉积，以及冲-洪积、风积和残积等。相应的覆盖层主要为第四纪的冲洪积物、坡积物以及残积物，主要分布于台地及丘陵区的沿海平原地区。南部观音山等区域为基岩出露区。

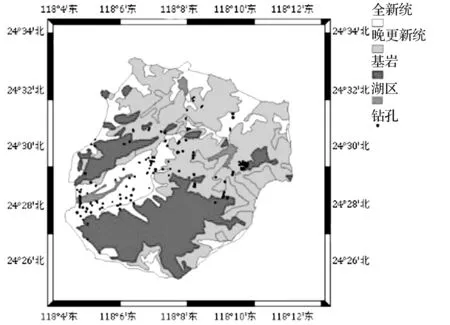
图1　厦门市工程地质及钻孔分布Fig.1 Engineering geology and boreholes in Xiamen

本文共搜集到202个钻孔资料，对应的剪切波速实测空间点2 100个。由图1可知，基岩区的钻孔较少，钻孔点主要集中在第四纪地质环境中，有利于建立土层的地质模型。钻孔揭示的土类主要包括填土、淤泥质土、黏土、粉质黏土、砂土和残积土等。按照实测钻孔点中出现的大致顺序，按上下顺序将厦门岛近地表土层划分为填土(T1)、黏性土(T2)、残积土(T3)、特殊类土(T4)和基岩(T5)共5层。其中，为方便建立土层模型，对其中数据点很少的黏土与粉质黏土归为T2，将集中在筼筜湖区的填土层与黏土层之内的淤泥与砂土归为特殊类土T4。各土层钻孔数据点数见图2。

图2　T1～T5土层的波速数据分布Fig.2 Distribution of Vs data in T1～T5

2　厦门岛工程场地剪切波速结构特征

2.1场地速度结构的空间相关性

自然界中的土体是在漫长的地质历史时期中经过复杂的地质作用而形成的地质体[10]。由于形成环境的相似性及动力地质作用的相继性，区域土体动力特性表现出明显的结构性和空间分布相关规律性。对同一区域场地两点间距越小，其成土环境的变化越小，两点之间的土层性质越相似，随着两点间距的增大，这种相关性逐渐减弱，甚至不相关[12]。

场地土层剪切波速作为场地土软硬程度和固结程度的具体表现，也同样具有这种空间相关规律性，遵从地质、地理信息的两条基本规律。一是在空间上具有一般的或平均的结构性质，在不同点间具有空间自相关性，这种相关性依赖两点间的距离，距离越近，联系越强；二是在一个地理空间系统内，因果关系制约着系统状态，系统状态除了受输入因子影响外，还部分受到其他区域的影响，具有局部的、随机的异常特征。

地学统计方法以区域化变量理论为基础，非常适合研究这种在空间分布上既有随机性又有结构性，或空间相关和依赖性的自然现象。最常用的克里格方法中，用协方差函数或半变异函数来表征这种空间相关性特征。图3为厦门工程场地剪切波速在不同方位角对应变异函数曲线分布。

图3　剪切波速在不同方位角对应半变异函数曲线分布Fig.3 The semivariogram of Vs in different azimuth angles of Xiamen engineering sites

2.2场地速度结构的带状异向性

带状异向性是指区域化变量在不同方向上的变异性差异较大。因其沉积环境条件的相近性和固结历史的相继性，工程场地土层水平方向性质和竖直方向有很大差异，相应的速度结构也具有明显的带状异向性。

图3中，右侧括号中参数表示空间克里格插值的搜索方位角的大小，其中第一和第二参数表示的是对水平两个方向的搜索方位角，第三个参数表示的是沿深度方向的竖向搜索方位角，这三个系数表示的是在插值过程中，椭球形搜索区间的方向转角。从图3中可以看出，当竖向搜索方位角Z=0时，沿X轴、Y轴、XY夹角45°方向的变异函数，在距离大于3 000 m(称为变程)时均稳定在一基本相同的平台上(称为基台)，基台值C值基本相同。且沿不同搜索方向的变异曲线的变程(曲线区域水平时对应的横轴值)均稳定在3 000 m～4 000 m，这说明在XY轴平面上剪切波速为各向同性的。而当竖向搜索方位角Z≠0时，对数据采用克里格插值法得到的拟合曲线均出现明显上升，没有稳定的基台值及变程，这说明剪切波速分布在Z轴方向有明显的带状异向性。这反映出了随着深度方向的土层类型发生变化，不同类别土的剪切波速变化明显。因此，为了避免这种不同土层剪切波速之间的差异性对建模的影响，应当按照不同类别土层分别单独建立其剪切波速分布模型。

3　建模方法

根据上述厦门岛波速结构分布特征，首先对各实测数据中的地质数据进行分类，确定各土层的分界面，以便在各层中进行空间克里格插值，建立场地三维工程地质模型。其次，在每一土层内部，对该土层钻孔点剪切波速数据，运用克里格插值，得到每层土体的空间剪切波速分布。最后，综合各个土层得到整体场地的三维速度结构模型。

3.1厦门本岛三维工程地质建模

首先对数据要进行分类整理，确定各种不同土体的基本层序，对钻孔数据进行分层后，再通过结合不规则三角网(TIN)法和克里格插值法，生成不同土层的分界面模型并进行平滑处理，最后利用场地土层的分界面建立空间三维地质模型。不规则三角网法是在地质地形方面运用的最多的建模方法，其主要是通过将一系列控制点组成三角形来构建地质面。各点通过一系列边两两相连，最终形成一个互不交叉的三角网，而这个三角网格即是真实地质面的数字模型。本文选用了Delaunay三角测量法。这种方法在建模过程中，会尽量确保模型中每个三角形的外接圆中没有其他测量点，如果整个三角网格都满足Delaunay原理，则可以保证模型中的三角形的最小角为尽可能最大化，即确保模型中没有太过狭长的三角形。由于实际勘察点数据的空间分布的不均匀性，形成的三角网通常很不规则，必须对其进行平滑处理。对土层面的平滑处理，本文选用普通克里格插值法。

三维地质模型的空间范围为一矩形区域(E118°03′-E118°11′，N24°25′-N24°33′)。将各钻孔点的经纬度坐标转换为平面坐标，以m为单位。模型的表面使用地表绝对高程，模型竖直方向高程范围：-53～46 m。对每一特定土层分界面的数据点进行克里格插值，得到在平面笛卡尔坐标系下的100 m×100 m的标准化网格点，确定每个土层的上下分界面。建立土层模型，利用土层分界面的标准网格点建立各土层的三维模型。各土层的三维模型见图4，整体模型见图5。

图4　厦门本岛各土层三维几何形态模型Fig.4 Spatial model of each layer in Xiamen Island

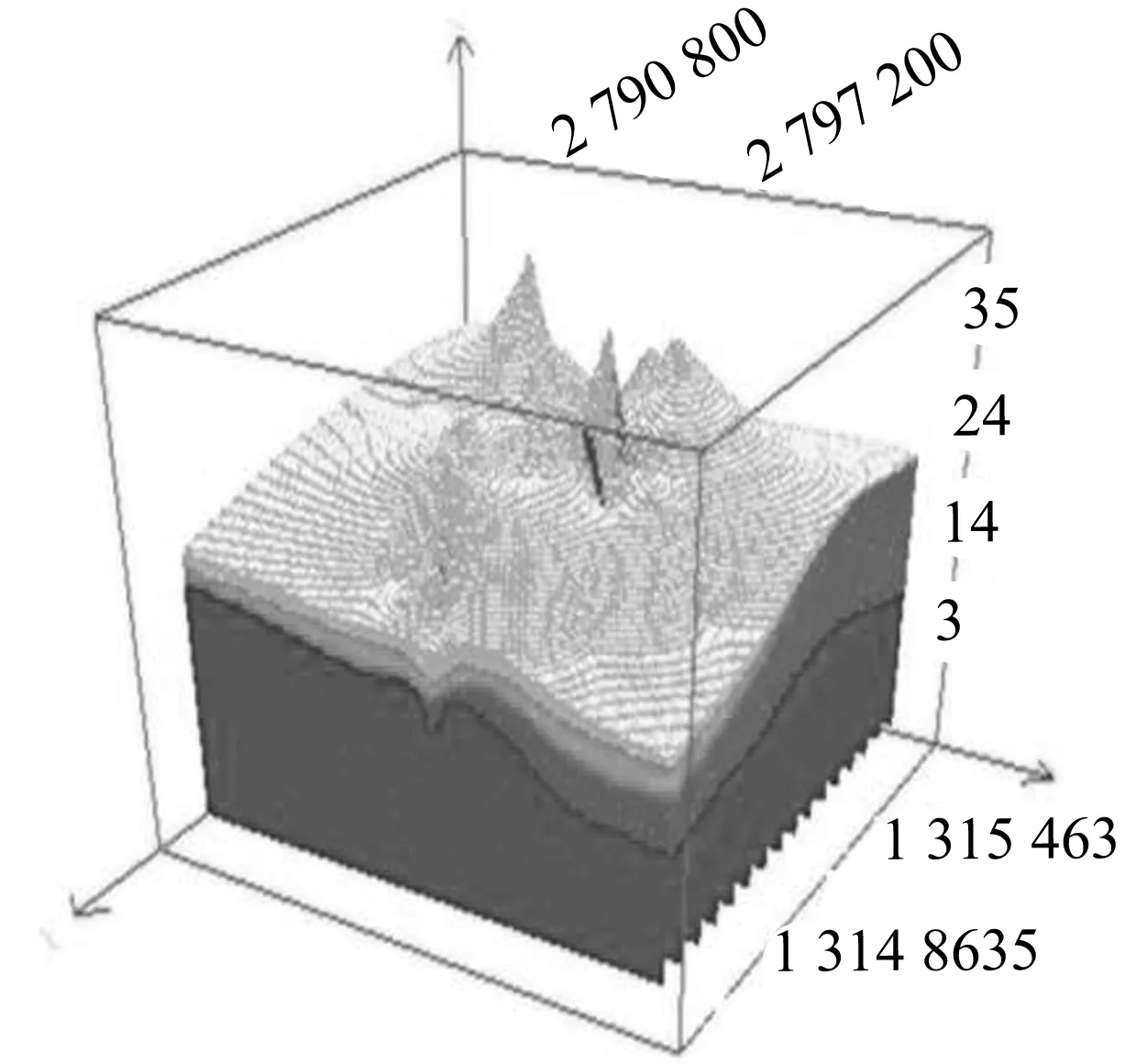
图5　厦门岛土层三维几何形态模型Fig.5 Soil 3D spatial model of Xiamen Island

图6　筼筜湖区各土层三维几何形态模型Fig.6 Spatial model of each layer in Yundang Lake

图7　筼筜湖区土层三维几何形态模型Fig.7 Soil 3D spatial model of Yundang Lake

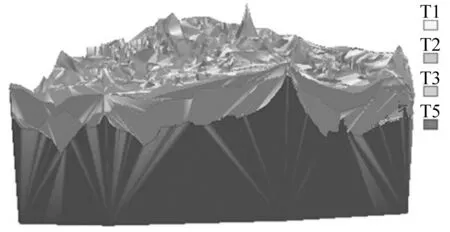
图8　御屏山南剖面土层三维几何形态模型Fig.8 Soil spatial model of south of Yuping Mount

插值结果基本反映了厦门岛的三维地质情况，选择筼筜湖区和御屏山南纵切面作地质剖面来分析。筼筜湖区各土层空间地质模型和全空间模型见图6和图7，御屏山南纵切面见图8。由图6和图7可知，土层按照基岩-残、坡积土-黏土-特殊类土-填土由下至上分布。以基岩层为基础层，在基岩峰之间，存在较厚的残坡积黏土层，而在残积土层上分布着少数黏土层。在黏土层上为淤泥和砂类土层，且在中部增厚。在剖面的表层分布着填土层，且填土层厚度比较均匀。

其分布特性的原因主要是，筼筜湖区原本是厦门岛的海湾，随着城市的发展，进行人工填海后使得筼筜海港成为筼筜湖，且在在该区域内第四纪沉积物之上人工进行回填土，因此在模型中黏土土上存在较厚的淤泥及砂层是符合实际的。由图8可知，御平山南剖面经过的土层按照基岩层-残、坡积土-黏土-填土由下至上分布。以基岩为基础层，在两侧基岩峰之间，存在较厚的残坡积土层，在残积土层上分布着黏土层，且黏土层沿基岩层山峰向两侧逐渐增厚，在剖面的表层分布着填土层，且填土层的厚度比较小。剖切线经过地区的为山地丘陵地区，基岩层一般比较高，保留有大量的残积土，黏土和填土较少等，建立的模型基本反映了实际的地质情况。

3.2厦门本岛剪切波速结构建模

依据已经得到的三维地质模型中的各土层土体的空间模型，将各土层的数据转化为标准化的网格点，得到各类土层的空间模型；对各土层中钻孔点的剪切波速数据运用克里格插值，得到每层土体的空间剪切波速分布；综合各个土层得到厦门岛工程场地的三维剪切波速模型。

克里格插值法要求数据分布呈正态分布。首先对剪切波速进行了对数变换。从图9可知，土层的剪切波速对数值更符合正态分布，仅基岩层(T5)因大量的钻孔点在钻入岩层后就停下，这些点的剪切波数据较小，使得剪切波速略集中在偏小一侧。

在取得其统计结果后，对各层数据建立变异函数模型。各土体中剪切波速对数值的半方差函数模型见图10。按照各向异性三维椭球面的方式进行搜索，将块金值设为0。根据顶点值确定各模型的基台值，得到变异函数模型中的各个参数，建立剪切波速模型。通过对图10进行分析，厦门本岛各类土的变程基本集中在3 500～4 500 m左右，与THOMPSON[9]所做的研究中加州地区的研究相近；而各类土的基台值不相同，即各模型的半方差值不一样，这体现各类土中剪切波速变化规律的不同。根据克里格插值法确立的各层内的剪切波速，整合各层得到的工程场地整体三维速度结构模型见图11及其半方差见图11。

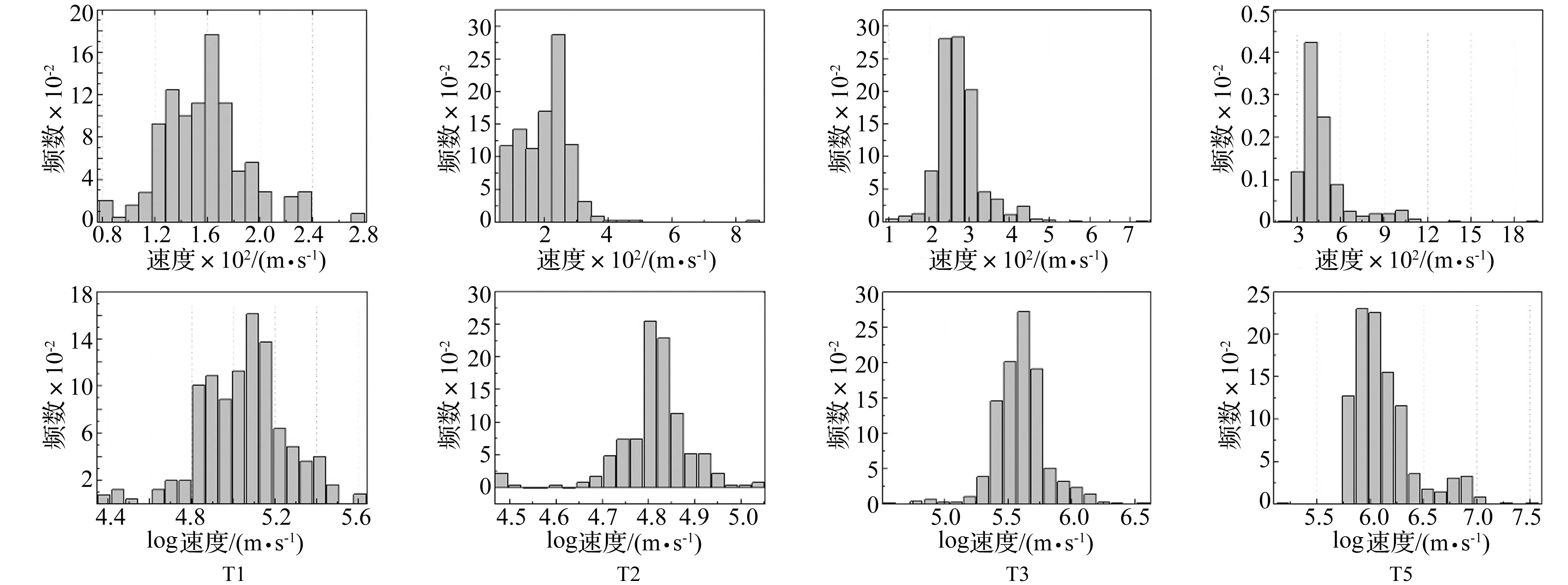
图9　钻孔点数据中各类土的剪切波速(上)及对数变换后波速统计图(下)Fig.9 Statistics of borehole Vs(up) and logarithmic Vs(down) for each layer

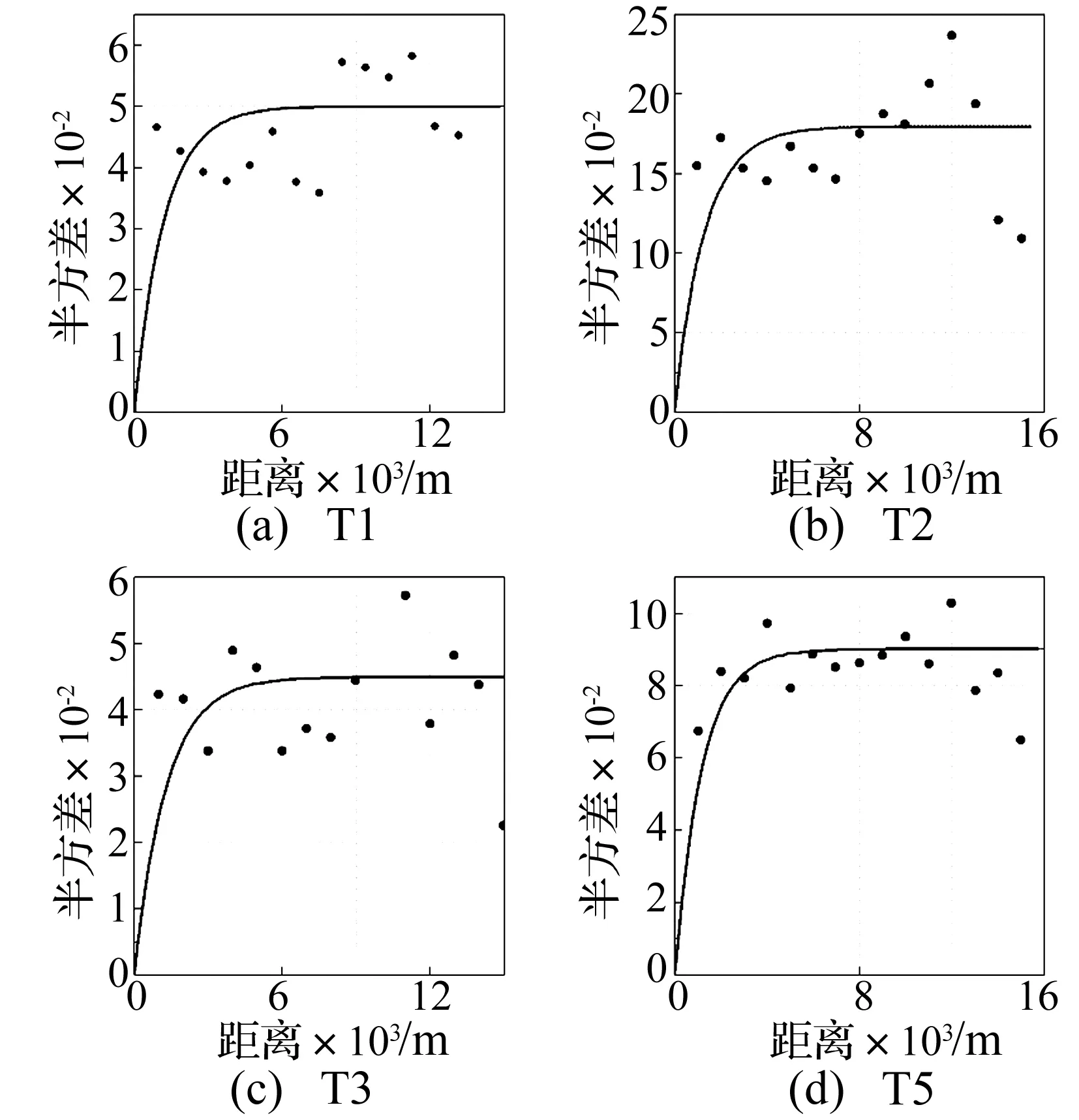
图10　各类土的剪切波速对数值在各向同性假定下的普通克里格插值的半方差模型Fig.10 The semi variance model of log(Vs) in each layer got from ordinary Kriging method in isotropic assumption

图11　三维剪切波速模型Fig.11 3D model of shear wave velocity

由图12可知，在建立模型的平面方向，区域的半方差值的大小与该区域周边的实际数据的多少密切相关，在模型中部区域，实际钻孔数据比较丰富，其半方差值均较小，在西北及东南区域，钻孔点数据较少，其半方差值普遍较大。在模型的垂直方向，由于钻孔数据在深度方向上，随着深度增加有效数据减小，使得在深度方向上，半方差值呈现上小下大的分布。

图12　三维剪切波速模型半方差图Fig.12 Semi variance of 3D Vs model

4　结果和分析

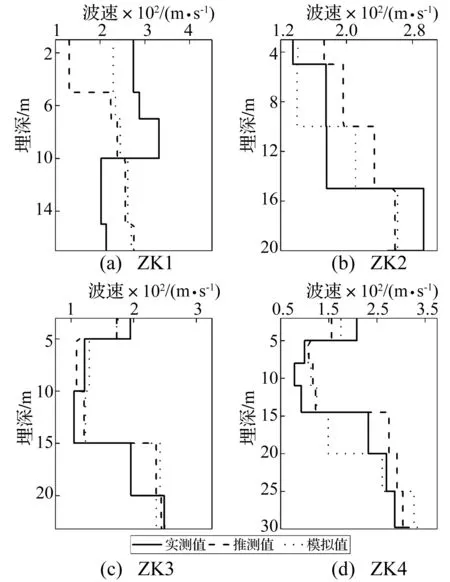
图13　随机钻孔点的实测剪切波速与拟合公式推测波速比较Fig.13 Vs Comparison in 4 boreholes

通过统计学建立的模型，实质上是对不确定性问题的一种估计方法，要确定模型所得的结果是否正确，则要用实际数据进行检验。随机选取未参与建模的4个实测钻孔点，对三维速度结构模型进行检验。实测剪切波速值与剪切波速推测值对比见图13。从图13中也可明显看出，由三维速度结构建模方法得到剪切波速推测值要明显优于直接通过剪切波速—埋深公式[11]给出的推测值，其中除有极个别的相对误差误差达到40%左右，大多数点的相对误差在30%以内，整体平均误差在20%以内。场地速度结构最重要的应用是评估场地的地震放大效应，而等效剪切波速Vs20是场地放大效应的主要评价指标。表1给出了分别根据钻孔点的实测剪切波速值、剪切波速—埋深公式推测值、实测值直接插值推测值以及三维速度结构模型推测值计算的等效剪切波速值Vs20。从表中可以看出，通过剪切波速—埋深公式得到的等效剪切波速的精度最差，其相对误差变化很大。对同一区域中，相同类型的土剪切波速也是变化的，这种统计关系仅能提供一个笼统的估计。而考虑了土层结构特性的三维剪切波速模型得到的等效剪切波速值，比根据实测钻孔点等效剪切波速直接插值给出的Vs20要明显更准确，即由三维速度结构模型推测剪切波速的方法效果更好。4个钻孔点覆盖层厚度均位于20～50 m之间。按照我国《建筑抗震设计规范》GB 50011—2010中的等效剪切波速对场地进行场地判别，可以得出ZK1、ZK2、ZK3的建筑场地类别为Ⅱ类场地，ZK4的建筑场地类别为Ⅲ类场地。根据本文所建立的速度结构模型计算的效剪切波速，判别的场地类别，与根据实测钻孔波速数据的判别结果是一致的。

表1　不同方法的等效剪切波速VS20对比表

5　结　论

厦门岛土层不同类别土存在明显的分层性，其对应的剪切波速也明显呈现分层性，具有明显的带状异向性，同一土层中的剪切波速具有很强的空间相关性。在工程场地剪切波速结构建模中，必须充分考虑速度结构大的空间相关性与带状异向性特征。本文在充分考虑滨海工程场地速度结构空间相关性和带状异向性特征的基础上，提出了能够反映剪切波速在土层内部变化规律的工程场地三维速度结构模型的方法，建立了厦门岛三维剪切波速结构模型。

通过随机选取的钻孔点对模型的检验表明，由三维速度结构模型得到的剪切波速推测值以及其等效剪切波速的值与钻孔数据的实测值更加接近，相对误差较小。通过先建立场地三维地质模型，再以地质模型中的土层分区建立剪切波速模型，最后整合各土层剪切波速模型，建立的三维剪切波速结构模型，能够反映工程场地近地表剪切波速的空间变化规律。模型中，钻孔数据较多的区域，半方差较小，拟合效果较好；而钻孔数据较少时，半方差较大，拟合效果较差。随着数据的增加，模型的可信程度将会增加。

[1] 刘福田,曲克信,吴华,等.华北地区的地震层面成像[J].地球物理学报,1986, 29(5): 442-449.

LIU Futian, QU Kexin, WU Hua, et al. Seismic tomography in north China region [J]. Chinese Journal of Geophysics,1986, 29(5): 442-449.

[2] SHEDLOCK K M, ROECKER S W. Elastic wave velocity structure of the crust and upper mantle beneath the north China basin[J]. Journal of Geophysical Research,1987,92(B9): 9327-9350.

[3] 朱露培,曾融生,刘福田.京津唐张地区地壳与上地慢三维P波速度结构[J].地球物理学报,1990, 33:253-269.

ZHU Lupei, ZENG Rongsheng, LIU Futian. Three-dimensional P wave velocity structure in Beijing-Tianjin-Tangshan area[J].Journal of Geophysical Research,1990, 33:253-269.

[4] 刘启元,李顺成,沈杨,等.延怀盆地及其邻区地壳上地慢速度结构的宽频带地震台阵研究[J]. 地球物理学报,1997,40(6):763-771.

LIU Qiyuan, LI Shuncheng, SHEN Yang, et al. Broadband seismic array study of the crust and upper mantle velocity structure beneath Yanhuai basin and its neighbouring region [J].Journal of Geophysical Research,1997,40(6):763-771.

[5] 莘海亮,方盛明,张元生,等.安阳及邻区三维地壳速度结构研究[J].地球物理学进展,2011(5): 1535-1543.

XIN Hailiang, FANG Shengming, ZHANG Yuansheng, et al.3D crustal velocity structure in the Anyang and its adjacent regions [J]. Progress in Geophysics,2011(5): 1535-1543.

[6] MAGISTRALE H, MCLAUGHLIN K, DAY S. A geology based 3D velocity model of the Los Angeles basin sediments[J]. Bulletin of the Seismological Society of America,1996,86: 1161-1166.

[7] 刘启方,李雪强,孙平善. 施甸盆地三维速度结构模型研究[J].地震工程与工程振动,2013,33(3): 88-94.

LIU Qifang,LI Xueqiang, SUN Pingshan, et al. Study on the 3D velocity model of Shidian Basin [J]. Earthquake Engineering and Engineering Dynamics,2013,33(3): 88-94.

[8] 师黎静.地脉动台阵观测三维速度结构反演与成像[D].哈尔滨:中国地震局工程力学研究所,2007.

[9] THOMPSON E M,BAISE L G, KAYEN R E, et al. A geostatistical approach to mapping site response spectral amplifications[J]. Engineering Geology,2010,114: 330-342.

[10] 薄景山,李秀领,刘红帅.土层结构对地表加速度峰值的影响[J].地震工程与工程震动,2003,19(2):11-15.

BO Jingshan, LI Xiuling, LIU Hongshuai. Effects of soil layer construction on peak accelerations of ground motions [J]. Earthquake Engineering and Engineering Dynamics,2003,19(2):11-15.

[11] 师黎静,苏茜.厦门本岛场地剪切波速相关性研究[J].地震工程与工程振动, 2014,34(增刊1):126-131.

SHI Lijing, SU Xi. Research on site shear wave velocity correlation in Xiamen Island [J]. Earthquake Engineering and Engineering Dynamics, 2014,34(Sup1):126-131.

[12] 高大钊.地基基础工程标准化与概率极限状态设计原则[J].岩土工程学报,1993,15(4):8-14.

GAO Dazhao. Standardization of foundation engineering and probabilistic limit state design approach [J].Chinese Journal of Geotechnical Engineering,1993,15(4):8-14.

A study on imaging the near-surface 3D wave velocities structure in the Xiamen Island

SHI Lijing1, SU Xi2, LIU Yushi1, LIU Heng3

(1. Key Laboratory of Earthquake Engineering and Engineering Vibration,Institute of Engineering Mechanics, China Earthquake Administration, Harbin 150050, China;2. HYH Architecture & Engineering Design Co. Ltd., Wuhan 430000, China:3. College of Transportation & Engineering, Nanjing Tech University, Nanjing 210009, China)

Based on 202-borehole data in the Xiamen Island, the characteristics of spatial correlations and zonal anisotropy of shear wave velocities(Vs) structure were analyzed. And an imaging method of 3D Vs structure was developed. In this method, the soil interfaces between layers was imaged first by the Delaunay triangulation and Kriging method to build the 3D geological model of the areas. Then the 3D Vs structures inside each layer were predicted by the Ordinary Kriging(OK)method. Finally the Vs models of each layer were integrated into a 3D model. The feasibility and accuracy of the method were verified by imaging 3D Vs structure of the Xiamen Island. The results show that the 3D Vs model is capable of reflecting both the Vs varying characteristics inside each layer and the zonal anisotropy of Vs between layers.

shear wave velocity; 3D model; ordinary kriging(OK)method; xiamen island

中国地震局工程力学所基本科研业务专项资金项目(2014B06);国家科技支撑计划项目(2015BAK17B01);黑龙江省自然科学基金(E2015068);国家自然科学基金(51308292);江苏省高校自然科学研究面上项目(13KJB130001)

2015-05-25修改稿收到日期：2015-07-21

师黎静 男，博士，研究员，1976年3月生

TU413.5

A

10.13465/j.cnki.jvs.2016.16.008