截流物损毁赔付计算方法的研究及其应用

邓铁军，宋玲，郝心童

(1. 湖南大学 土木工程学院，湖南 长沙 410082；2. 武汉大学 土木建筑工程学院，湖北 武汉 430072)



截流物损毁赔付计算方法的研究及其应用

邓铁军1，宋玲1，郝心童2

(1. 湖南大学 土木工程学院，湖南 长沙 410082；2. 武汉大学 土木建筑工程学院，湖北 武汉 430072)

基于工程险通用保险合同的一般约定条款建立工程险赔付计算模型，探讨截流物损毁赔付计算模型中标的损失 、减损费用 等参数的确定方法，基于散体力学和河流动力学分析截流物失稳垮塌临界状态下的流速与截流物体的变化关系，建立灾后截流物损失量估算模型，提出截流物损毁赔付计算的方法。并将损失量估算模型与损毁赔付计算方法应用到具体的截流物工程赔付案例中，验证了模型及方法的可行性与适用性。

截流物；损毁赔付；计算方法；估算模型

桥梁工程、水利工程等因建造需要而要构筑施工便道、筑岛等截流用临时工程，这些截流用工程因其临时性既要实现截流后施工目的又要节约成本，时常难以抵抗不可预见的洪灾冲击，故而施工单位常将其作为投保建筑工程一切险的内容。在承保期间，洪灾冲击损毁时有发生，而保险公司因缺少专业人士常驻施工现场，致使灾后勘验资料不足，无法准确地计算损毁损失、确定理赔额，从而发生理赔争议，只好通过诉讼方式解决。而法院处理此类案件中往往委托专业机构对损毁损失进行评估，因此，如何科学地对截流物损毁损失进行评估、正确的确定损毁量是一个很重要的课题。目前，有关保险理赔的研究主要集中在保险制度、理赔流程、保险中介及费用组成等方面。Gaafar等[1]对保险赔偿责任进行了分析，研究了合同责任条款应具备的法律地位；马士勇[2]提出规范工程保险体系、全方位推动保险制度的建议；Kamardeen[3]对理赔陷阱、免赔事项等进行了讨论；杨明亮[4]提出应委托保险公估人等专业人士来进行损失的评估，以利于评估结果的科学性与公正性；华建斌[5]在讨论工程保险理赔费用文章中，提出损失费用应由直接经纪费用、施救清理费用、修复费用及其他费用组成。这些研究都是设定理赔勘验到位、资料齐全的前提下进行的，往往与现实工程灾后状况不相符，且在研究中没有对具体的灾后状况提出相应的理赔计算方法，更没有针对截流物在洪水灾害后损失量及其相应的赔付计算方面的研究。对于理赔勘验不到位、资料不足的截流物灾后理赔，本文建立了赔付计算模型，提出了洪灾后水中截流物(施工便道、筑岛等)损失量的估算方法。

1　工程险赔付计算模型的建立

在工程领域中，工程险一般是指建筑(安装)工程一切险及其附带的第三者责任险。本文依据通用保险合同的一般约定[6]着重对前者理赔发生后的赔付额的计算进行研究。

理赔过程中，保险公司要严格按照合同约定进行赔付，在确保自身利益的同时保证被保险人的损失得到应有的赔偿，但实践中因事件的复杂性，而对合同的理解往往难以达到共识。由此基于合同确定恰当的赔付计算模型，是解决赔付事件的首要工作。

通用保险合同一般约定条款中有关赔付的要求有：

1)理赔的财产应同时满足在保险单中明确列出、除外责任以外的自然灾害及意外造成的损失、损失发生在指定承保的工地范围内3个条件。赔付部分可以分为标的损失(S)及被保险方为防止或减少标的损失所支付的必要的、合理的费用(H)；

2)足额投保即投保的保险金额(M)与标的价值(C)相等时，按实际损失进行赔偿；非足额投保时，按保险金额占标的价值的比例进行赔偿；

3)无论是采用恢复到损失前的费用扣除残值后的支付赔偿，还是采用修复赔偿、重置赔偿，赔付额都不能超过其保险金额；

4)如果采用同一标的由多个保险公司承保的重复投保方式时，则各保险公司以其承保的保险金额(Bi)占总保险金额(B)的比例为依据分摊赔付额(Pi)。

5)如果合同约定了免赔额(M)或免赔率(γ)，那么只有当保险公司应赔偿的损失超过了免赔额或根据免赔率确定的免赔额时，才负责赔偿。若免赔额(或免赔率)是绝对免赔，保险公司只赔偿超过免赔额的部分，当免赔额及由免赔率确定的免赔额同时存在时，选择两者中大的免赔；如果免赔额(或免赔率)是相对免赔，保险公司则全额赔偿。

根据上述要求体现的相关关系，本文建立的针对通用合同一般约定条件下的工程险赔付计算模型为：

(1)

2　截流物损毁赔付计算模型参数的确定

桥梁工程、水利工程等建造中构建施工便道、筑岛等截流物工程，损毁赔付的计算模型适用于本文公式(1)所建立的计算模型。但应结合具体工程确定计算模型的相关参数，主要是标的损失S及被保险人为防止或减少标的损失所支付的必要的、合理的费用H及相关参数。

2.1标的损失S及必要的减损费用H的计算

标的损失S一般按照原合同认定的造价原则进行计算。确定当中，可将标的损失划分为计算工程量部分(K)和核定成本部分(U)。计算工程量部分的费用按该部分工程量(Gi)乘以相应的成本单价(Di)计取，核定成本部分的费用由被保险人提供的相关费用凭据确认。标的损失可以表示为：

(2)

式中：Cj是指第j项被保险人提供的相关费用凭据。 成本单价Di包括人工费(r)，材料费(c)，施工机具使用费(s)和管理费(g)，即：

Di=r+c+s+g

(3)

必要的减损费用H也可按照标的损失S的确定方法进行计算，具体计算方法参照公式(2)和公式(3)。

2.2工程量的确定

工程量的确定，如果理赔勘察到位、过程资料记载齐全及跟踪到位，可以直接根据过程相关资料及勘察结果编制工程量损失清单，按照工程量清单计量规则计算各部分的工程量即可。但是，在实际理赔过程中，保险公司由于理赔机制不完善、专业人员不足，无法实施过程跟踪，导致出险后难以获得准确的勘验结果，而被保险人出于自身利益考虑，为获取高额赔偿，出险后提供的相关资料难以确保其客观性和真实性。

截流物在正常工作状态时处于受力平衡的稳定状态，当发生水毁时，是由于受洪水冲击导致失稳和垮塌。分析出现失稳垮塌的临界状态下流速与截流物的变化情况及相关关系，从而建立损失量估算模型，估算损失发生范围，然后按照工程量清单计量规则计算出各部分损失量，最后根据赔付计算模型确定赔付额。

3　灾后截流物损失量估算的理论研究

3.1损失发生时的临界流速

在桥梁与水利工程中截流物主要是指施工便道、筑岛等临时工程，它们一般是由性质大致相同的颗粒(填土、砂砾石、鹅卵石等)组成的集合体，属于散体堆砌物[7]。根据水力学原理，一颗静止于床面的颗粒主要受到其水下重力、水流作用力和床面反力的综合作用，当颗粒开始起动时的状态可以用拖曳力、平均流速和水流功率表示[8-10]。

假定水流强度特别大时，截流物的组成颗粒是成层运动的，则可以利用推移质理论中的起动流速来描述使截流物的组成颗粒从静止状态转为运动状态的水流平均速度[11]，其大小为：

(4)

式中：vL为起动速度，m/s；k和α为常数，根据清华大学水利系在长江某站测得的研究资料，推移质为卵石时，k取0.278，α取0.475；h为推移质离水平面的高度，m；d为固体的粒径，m；rs固体物质的容重，N/m3；r为水的容重，取9.8 kN/m3；g为重力加速度，取9.8 m/s2。

由公式(4)确定的水流平均速度即可认为是截流物损失发生时的临界流速。

3.2损失范围及损失量的确定

3.2.1损失范围的分析

陈森林[12]以河道最深处x0为分界点将河道分为左右两部分，并以左岸为基准点(基准点随着高程的改变而不同)建立了河道断面流速分布函数：

(5)

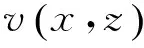
根据公式(5)可知，河道断面的同一高程上的水流速度向水位最深处逐渐递增，在x0处达到最大，河道断面任一垂线上的水流速度随着高程的增加逐渐递增，在靠近水面处达到最大(如图1所示)。并且x0左边(右边)不同高程上距离左岸(右岸)基准点水平距离相等的点的水流速度相等，x0处垂线两边水流速度连续。如果将水流速度相等的点连接起来可以得到一条条与河道断面形状相似的曲线，这些曲线为等速线。

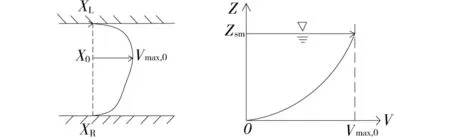
图1　河道断面的流速变化Fig.1 Velocity variations of the river cross-section

由于天然河道断面形状极不规则，很难用精确函数描绘出来，根据实测的大断面图可将其简化为多个梯形断面与抛物线或三角形的组合。本文首先将河道简化为一个梯形和两段抛物线的组合，结合所提出的等速线进行研究，得到河道断面等速线图如图2所示，河道断面两边越靠近x0处的等速线上的水流速度越大。

图2　河道断面的等速线图Fig.2 Flow-velocity contour lines of the river cross-section

由此，理想状态下的截流物损失范围就是水流速度超过其起动流速的部分，也就是起动流速构成的等速线所包围的部分，如图3所示的截流物阴影部分。

图3　截流物的损失范围Fig.3 Loss of the closure

3.2.2损失量估算的分析

以河道断面简化图形中梯形部分和抛物线部分的分界线为x轴，x0点垂直方向为y轴建立坐标系。截流物横截面一般为梯形，如果其上顶面宽为a，两边边坡坡度分别为i1和i2，临界流速构成的等速线函数为fv(x)，则损失大小的估算模型为：

V=∫S(x)dx=

(6)

当x0位置不确定时，为确保被保险人的利益，应取使损失量V最大的位置为x0。

3.3临界流速的等速线方程的确定

根据以上研究可知，临界流度构成的等速线函数与河道断面函数有关。设河道断面分布函数为：

式中，xA和xB分别为河道断面梯形部分与抛物线部分两交点的横坐标。

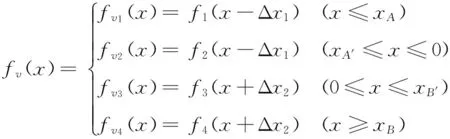
(7)

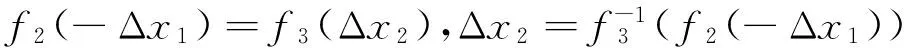
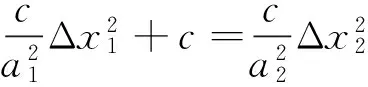
因此，已知河道断面分布函数f(x)求临界流速等速线的分布函数fv(x)，只需要知道Δx1或Δx2即可。有以下2种方法：

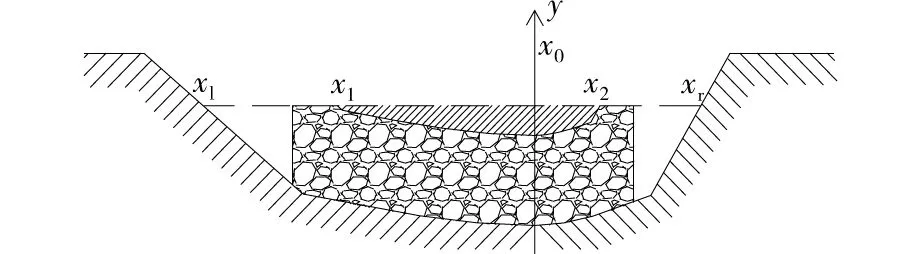
图4　截流物的损失大小Fig.4 Loss of the closure

2)根据水流速度确定fv(x)

①若x0的具体位置未知，在洪水期间，选取截流物附近多点测量水流速度，将获得的数据代入式(5)中求出a，b，c和d，得到河道断面水流速度分布函数，然后将式(4)求出的临界流速vL代入分布函数中，即可得到临界流速的等速线分布函数fv(x)。

②若x0的具体位置已知，由于x0垂线(即y轴)上各点水流速度符合指数分布，则设x0上各点流速为：

(8)

(9)

4　应用分析

某铁路扩能改造工程GTXG-3标段足额投保建筑工程一切险及第三者责任险，投保金额为95 395.55万元，洪水、暴雨等特种危险赔偿限额为总保额的80%，每次出险免赔额为50万元且为相对免赔额。在保险合同期限内该标段发生一次洪灾后紧接着发生了第2次洪灾，导致施工便道、筑岛围堰等临时工程发生损失。出险后被保险人申请该临时工程全部毁坏的赔偿金额为820.43万元，保险公司勘验后认为并未完全损毁，不认可赔偿额，但因资料不足、专业手段有限，无法确定损失大小，双方协调不下，最后诉至法院。法庭上，被保险人根据已有资料提出的赔偿额为500.00万元，但保险公司仍有异议，经法院协调，双方同意由法院委托专业机构进行损失评估鉴定。

为了检验提取mtDNA的纯度，本研究参考大豆已知基因NARK、psbC和Cox Ⅲ的序列，设计了3对引物(表1)，分别以提取到的mtDNA和大豆基因组DNA为模板，进行PCR扩增。电泳检测结果发现，提取到的mtDNA只有Cox Ⅲ序列引物扩增出了目的条带，而基因组DNA中3对引物均扩增出目的条带(图5)，说明所提取到的mtDNA纯度较高，无核基因组DNA和叶绿体DNA的污染。

鉴定过程中，鉴定人对被保险人提供的理赔资料进行梳理，基于保险公司的相关资料得到要求赔偿的项目、金额及其原因的情况分析如表1所示。

表1中第5项费用不应计算，第3项费用不能根据既有资料准确计算，在分析理赔条件的基础上，应用本文模型对第3项费用进行了估算，估算结果被法庭采用，双方当事人无异议。具体算法如下：

首先计算施工便道的损失工程量。在常水位下，该标段大桥2-6号墩处于水中，其中3-4号墩位的河道较深，高程约在76～78 m，5-6号墩位的河道较平坦，高程约为78.6 m。1-7号墩的施工便道顶部高程为85 m，洪灾后施工便道只在靠近两岸部分有残余，且残余长度相差不大，根据判断取两岸残余长度Δx1=Δx2=42.97m。取3-4号墩位中点处的河底为最深处，高程为76 m，河道断面图简化由梯形和抛物线形组成(如图5所示)，以梯形底边为x轴，最深处的垂线为y轴建立坐标系。其中，抛物线部分为2-3号墩位中点到4-5号墩位中点，最低点为(0,-2.6)。

表1　理赔资料分析

图5　河道断面的简化模型Fig.5 A Simplified model of the river cross-section

根据相关资料，河道宽417.3 m，左岸坡度约为0.58，右岸坡度约为0.72，A(-144.08，0)，B(226.77，0)，D(-80，0)，E(80，0)，则河道断面函数为：

则施工便道临界流速的等速线方程为：

施工便道损失部分为图中阴影部分(如图6所示)。

图6　施工便道的损失部分Fig.6 Loss of the construction Road

施工便道横截面为上顶面为7 m，两边放坡1∶0.75的等腰梯形，所以施工便道损失工程量为：

V=∫S(x)dx=

21 745.2m3

筑岛的损失工程量按照同样的算法进行，3号及6号筑岛损失的估算工程量分别为8 633和1 470.7 m3。

1-7号墩施工便道及3号和6号墩筑岛损失大小如表2所示。

属于保险公司承保范畴的损失为：

425 463+37 343.6+461 871+2 166 401=

3 091 078.6 元

由于保险为足额投保，损失金额高于免赔额且在赔偿限额内，因此保险公司应赔偿3 091 078.6元。该评估计算结果提交法院后为原被告双方所接受。

表21-7号墩运输便道及3号和6号墩筑岛损失大小

Table 2 Losses of the construction road of the No.1-7. pier and the islands of No.3. and No.6. pier

序号项目名称单位单价数量价值/元备注11-7号墩施工便道m390.021745.21957068.023号墩筑岛m390.08633.076970.036号墩筑岛m390.01470.7132363.04合计元2166401

5　结论

1)基于建筑(安装)工程一切险通用保险合同一般约定条款中有关赔付的规定，对不同的理赔方式建立了统一的工程险赔付计算模型，为灾后处理理赔赔付损失提供了理论计算方法。

2)施工便道、筑岛等截流物是桥梁、水利工程中常见的临时工程，洪灾发生后经常出现损毁。对截流物损毁赔付计算时涉及模型的标的损失S和减损费用H等参数的确定进行了讨论。

3)针对理赔过程中发生的理赔机制不完善、无法实施过程跟踪、专业人员及其手段不足、洪灾后资料不全的截流物工程，基于散体力学和河流动力学理论对其灾后损失估算的方法进行了理论研究，建立了截流物灾后损失估算量模型。并结合具体的截流物工程赔付案例进行了应用，验证了估算方法的适用性。

[1] Gaafar H K, Perry J G. Limitation of design liability for Contractors[J]. International Journal of Project Management, 1999,17(5): 301-308.

[2] 马士勇. 中国建设工程保险体系与实施策略研究[D]. 成都：四川大学, 2006

MA Shiyong. Insurance system of construction Project of our country and study on implementing the tactics[D]. Chengdu: Sichuan University, 2006.

[3] Kamardeen Imriyas. An expert system for strategic control of accidents and insurers’ risks in building construction projects[J]. Expert Systems with Applications, 2009, 36(2):4021-4034.

[4] 杨明亮.在公路建设中引入工程保险的政策建议[J]. 交通企业管理, 2006,245(8):36-38.

YANG Mingliang. The construction suggestions of introducing engineering insurance in highway[J]. Transportation Enterprise Management, 2006,245(8):36-38.

[5] 华建斌.工程保险理赔方法浅谈[J]. 安徽建筑, 2011,226(4):217-218.

HUA Jianbin. Discussion on engineering methods of insurance claims[J]. Anhui Architecture, 2011,226(4):217-218.

[6] 全国人民代表大会常务委员会.中华人民共和国保险法[Z]. 2015-4-24.

The Standing Committee of the National People’s Congress.Insurance Law of the People's Republic of China[Z]. 2015-4-24.

[7] 王兴奎，邵学军.河流动力学[M].北京：科学出版社，2004.

WANG Xingkui, SHAO Xuejun. River dynamics[M]. Beijing: Science Press, 2004.

[8] 吴爱祥, 孙业志, 刘湘平. 散体动力学理论及其应用[M]. 北京：冶金工业出版社，2002.

WUAi xiang, SUN Yezhi, LIU Xiangping. Granular dynamic theory and its application[M]. Beijing: Metallurgical Industry Press, 2002.

[9] 戴清，刘春晶.希尔兹曲线的拟合及不确定性研究[J].泥沙研究，2014,354(6):19-24.

DAI Qing, LIU Chunjing. Study on the curve-fitting for the Shields diagram and its uncertainty[J]. Journal of Sediment Research, 2014,354(6):19-24.

[10] 何文社, 方铎. 泥沙起动流速研究[J]. 水利学报, 2002,562(10):54-56.

HE Wenshe, FANG Yi. Study on incipient velocity of sediment[J]. Journal of Hydraulic Engineering, 2002,562(10):54-56.

[11] 张红斌. 泥沙起动流速的统一公式[J].水利学报，2012,43(12):1387-1396.

ZHANG Hongbin. A unified formula for incipient velocity of sediment[J]. Journal of Hydraulic Engineering, 2012,43(12):1387-1396.

[12] 陈森林.河道断面流速分布函数研究[J]. 水利学报，1999,520(4):70-74.

CHEN Senlin. Study on velocity distribution function of river section[J]. Journal of Hydraulic Engineering, 1999,520(4):70-74.

Research and application of the calculation model ofinsurance claim for the damaged closure

DENG Tiejun1, SONG Ling1, HAO Xintong2

(1. School of Civil Engineering, Hunan University, Changsha 410082, China;2. School of Civil and Architectural Engineering, Wuhan University, Wuhan 430072, China)

Based on the general provisions of the general insurance contract of engineering insurance, the model of engineering insurance compensation calculation was established. The determination of the parameters in the model was discussed, including the loss of insurance and the cost of reducing losses. Furthermore, the estimating model was established after examining the relationship between the current velocity and the closure at critical state of the closure’s loss of stability with the granule mechanics and the river dynamics. The method of calculation of the closure property damage compensation was put forward. Then the loss estimation model and the calculation method of insurance claim for damaged closure were applied to the specific project closure payment case, and the feasibility and applicability of the model and method were verified.

the closure; insurance claim for damages; calculation model; estimating model

2016-02-28

湖南省发改委重大课题项目(20151JDJB02)

邓铁军(1960-)，男，四川夹江人，教授，从事建筑工程施工与经济管理及工程项目管理研究；E-mail:dengtiej@163.com

F842.4

A

1672-7029(2016)08-1652-07