槽型轨磨耗演变过程数值模拟

杨阳，李芾，张茂松，丁军君

(西南交通大学 机械工程学院，四川 成都 610031)



槽型轨磨耗演变过程数值模拟

杨阳，李芾，张茂松，丁军君

(西南交通大学 机械工程学院，四川 成都 610031)

为研究槽型轨磨耗规律，采用多体动力学分析软件UM，基于Specht磨耗模型及轮轨多点接触理论以我国自主研发的70%低地板有轨电车为例，建立59R2槽型轨磨耗计算模型，分析槽型轨在缓和曲线、圆曲线、直线地段的磨耗情况。计算结果表明：圆曲线外侧轨道的磨耗主要集中在轨肩处;当列车通过次数较少时内侧轨道磨耗主要集中在轨头及轨肩处，随着列车通过次数增加磨耗量变大，轨槽磨耗量与轨头及轨肩的磨耗量基本相当；缓和曲线轨道的磨耗量远小于圆曲线上轨道的磨耗量，外轨磨耗集中于轨肩处，内轨集中在轨头及轨肩处；在直线地段上，左右侧轨道的磨耗情况基本相似，磨耗量远小于圆曲线和缓和曲线。

槽型轨；有轨电车；钢轨磨耗规律；多点接触理论；数值模拟

低地板有轨电车由于其线路建设成本低、节能环保无污染、乘坐方便等优点在国内越来越多的城市开始规划和投入使用，在缓解日益拥堵的交通问题中发挥越来越重要的作用。为了节省道路资源，低地板有轨电车一般同其他车辆共享路权，故有轨电车线路一般使用槽型轨，与普通钢轨不同槽型轨轨头处有一个不对称的轨槽如图1所示。槽型轨在铺设过程中能与公路路面平顺衔接，内侧轨槽可以限制轮对的横向运动能够起到一定的安全作用，防止车辆脱轨，行驶稳定性强，是有轨电车线路的最佳选择[1]。

磨耗是轮轨系统固有存在的现象，槽型轨也不例外，但城市有轨电车线路的显著特点是小半径曲线较多，这使轮轨磨耗问题更加突出。轮轨磨耗引起轨道外形发生变化，轮轨接触状态及车辆的动力学响应发生改变，严重的钢轨磨耗会引起车辆脱轨等严重的安全事故[2-3]。当钢轨磨耗到限时需要更换钢轨，将直接影响乘客出行，增加运营维护成本。国内外学者在轮轨磨耗的数值仿真及试验测量方面已做了大量的研究，主要集中在车轮踏面磨耗，在钢轨磨耗方面的研究成果较少。Zobory等[4]在现场统计数据及车轮磨耗试验的基础上建立了Zobory磨耗模型并应用于轮轨磨耗；DING等[5]基于半赫兹接触理论、FASTSIM算法和Zobory磨耗模型法对重载货车车轮磨耗进行预测仿真，并与实测结果进行比；王璞等[6]利用多体动力学软件UM，基于Specht材料磨损模型对钢轨磨耗进行计算，研究重载铁路不同地段钢轨磨耗的发展规律。槽型轨比普通轨道在轨道内侧多出轨槽，在运行过程中由于轨道激励和曲线等因素车轮轮背与槽轨内侧可能发生接触，因此槽型轨的轨头、轨肩、轨槽均会发生磨耗。这在我国某地正在使用的70%低地板有轨电车线路上已得以印证。在研究槽型轨的磨耗规律时，以某新型70%低地板有轨电车为研究对象，由于要考虑轮背与轨槽的接触问题，传统的轮轨接触力计算模型已不能满足计算要求，故本文基于轮轨多点接触理论及Specht磨耗模型对槽型轨磨耗行研究。以期通过数值仿真对槽型轨的磨耗过程进行预测，为运营部门对槽型轨的维护工作提供依据，降低经济成本，减缓钢轨磨耗。

图1　槽型轨示意图Fig.1 Schematic of groove track

1　槽型轨磨耗计算模型

以国内自主研发的新型70%低地板有轨电车为研究对象，采用多体动力学分析软件UM建立车辆系统动力学模型，在动力学模型的基础上基于Specht磨耗模型计算钢轨型面磨耗演变过程。

1.1车辆轨道耦合动力学模型

该车采用“M+TP+M”三模块编组形式如图2所示，2个车体模块之间使用上下铰接使其形成静定结构。连接铰具有以下几种形式：固定铰，类似于球铰限制3个方向的平动，可以传递垂向、横向及纵向力，可绕3个方向转动；自由铰，仅限制车体间的侧滚运动；转动铰，限制相邻车体间的横向和纵向平动，各铰接装置如图3所示。

图2　低地板有轨电车Fig.2 Low-floor tram

(a)固定铰；(b)转动铰；(c) 自由铰图3　铰接装置图Fig.3 Hinged equipment

该70%低地板有轨电车转向架设计方案如图4所示。为适应车辆与转向架之间的大转角动力转向架采用带摇枕结构，在摇枕与车体之间装有弹

性旁承及中心销如图4(a)所示；非动力走行部走行部直接通过二系橡胶堆与车体相连接，每轴上装有2个制动盘如图4(b)所示。

基于多体动力学理论，在动力学分析软件UM中建立整车动力学计算模型。该车采用国内常用的59R2槽型轨，因国内尚无适用于槽型轨的标准踏面，故为该有轨电车设计了非标准踏面。车辆在运行过程中由于轨道激励和曲线等因素车轮踏面与轨顶及车轮轮背与槽轨内侧可能同时发生接触，为了能够精确计算整个槽型轨型面各处的磨耗情况，在动力学计算时使用多点非椭圆接触理论[7]计算轮轨力。建立完成的动力学模型如图5所示。

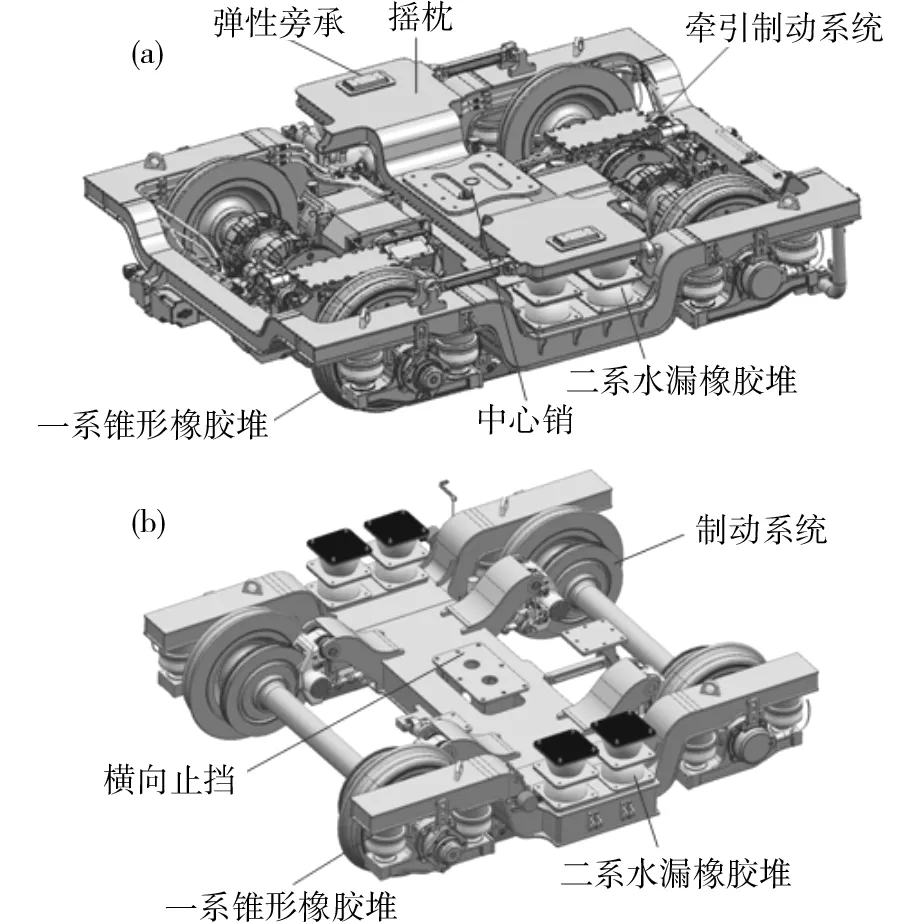
(a)动力转向架；(b)非动力转向架图4　转向架方案图Fig.4 Powered and non-powered bogies of vehicle

图5　车辆动力学计算模型Fig.5 Model of vehicle dynamic

1.2槽型轨磨耗计算模型

槽型轨型面磨耗演变过程仿真模型主要包括车辆轨道动力学仿真模型、轮轨接触关系计算模型、轨面磨耗计算模型和型面更新模型等部分，整个计算流程如图6所示。

通过多体动力学仿真程序计算轮轨接触斑内各单元的受力情况，根据磨耗模型计算各单元格内的磨损情况，最终再累加到槽型轨外型上。本文在计算时选用Specht磨耗模型[6,8-9]对槽型轨的磨耗演变过程进行计算，该计算模型假设磨耗体积与磨耗功线性相关，根据磨耗程度不同将磨耗区域分为轻度磨耗和重度磨耗两个区域，不同区域对应着不同的磨耗系数：

图6　槽型轨型面磨耗演变过程仿真模型流程图Fig.6 Scheme of wheel wear simulation

(1)

其中:I为磨耗量;kV为轨道长度方向上微段上的磨耗功；A为体积损伤因子；α为跳跃系数；w为轮轨摩擦功率；wcr为临界功率。损伤因子的取值受多种因素的影响，根据文献[6]和[9]取A=10-13m3/J,α=10,wcr=4 W/mm2。

由于槽型轨型面的磨耗量是连续增加的，在数值仿真时不可能做到实时更新，只能动力学计算一次进行m磨耗分析计算，当达到型面更新条件时进行车轮踏面更新，本文采用车轮的磨耗深度达到0.1 mm作为型面的更新条件。

2　槽型轨型面磨耗发展规律

根据车辆实际运行线路，选择半径为50 m的曲线路线作为分析对象，其中缓和曲线30 m，车辆以平衡速度通过。进行直线工况计算时考虑到低地板有轨电车线路一般为新修线路且仅有一种车辆运行线路条件较好，故激励选择为德国高干扰谱。

2.1圆曲线地段

圆曲线上的内外侧轨道原始型面及磨耗后的型面及车辆通过不同次数后型面累计磨耗量如图7～8所示。

对于曲线外侧轨道，磨耗主要集中在轨肩处，当列车通过15 404次时最大磨耗量为2.5 mm，从图7(b)中可以看出，当车辆通过11 252次时槽型轨内侧轨槽发生轻微磨耗，这主要是由于车辆通过曲线时转向架的状态造成的，车辆以低速通过曲线时后轮对可能贴靠内轨，随着磨耗量增加后轮对可以产生的横移量增加，曲线外侧车轮轮背与槽型轨内侧轨槽发生接触，产生磨耗，但是该磨耗量较小。

对于曲线内侧轨道，当列车通过次数较少时如图8(b)中8 550次，磨耗主要集中在轨头及轨肩处，随着列车通过次数增加磨耗量变大，轮对在轨槽内的横移量变大，车轮轮背与槽型轨内侧发生接触产生磨耗，列车通过次数再增加槽型轨内侧轨槽磨耗加剧，轨槽磨耗量与轨头及轨肩的磨耗量基本相当。槽型轨轨肩处磨耗与文献[6]中普通轨道有所不同，主要原因是由于文献[6]中曲线半径设置较大运行速度较高，转向架后位轮对不会贴靠内侧轨道的原因。

槽型轨轨槽内侧轨宽度较窄，发生大量磨耗对槽型轨十分不利，从保护轨道的角度出发，当车辆运行一段时间后，在不对车辆动力学性能产生巨大影响的情况下增加轮对轮背内侧距以减小对轨槽的磨耗。

(a)轨道型面变化;(b)轨道累积磨耗量图7　圆曲线外侧轨道Fig.7 Outside track of circular curve

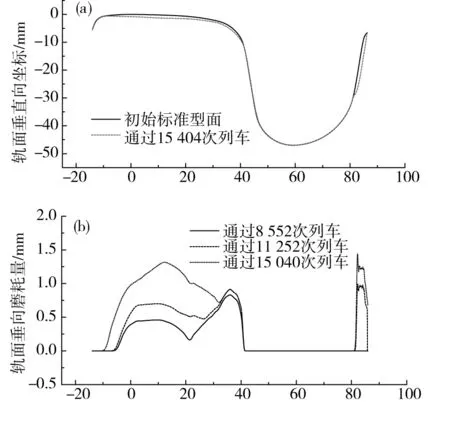
(a)轨道型面变化;(b)轨道累积磨耗量图8　圆曲线内侧轨道Fig.8 Inner track of circular curve

2.2缓和曲线地段

缓和曲线上的内外侧轨道原始型面及磨耗后的型面及车辆通过不同次数后型面累计磨耗量如图9～10所示。曲线外侧轨道磨耗主要集中在轨肩处如图9(b)所示，列车通过23 910次时最大磨耗量为2.5 mm，曲线内侧轨道磨耗主要集中在轨头及轨肩处如图10(b)所示，但其磨耗深度远小于外侧轨道仅0.88 mm。缓和曲线轨道的磨耗量远小于圆曲线上轨道的磨耗量。

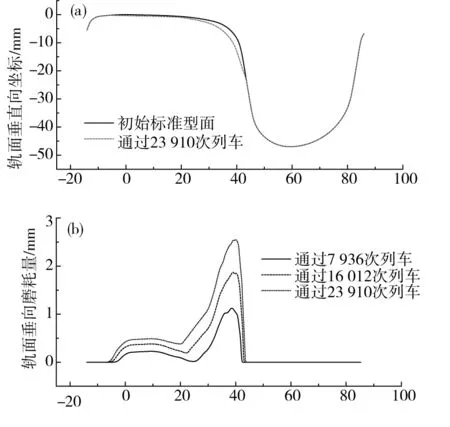
(a)曲线外侧轨道型面变化;(b)曲线外侧轨道累积磨耗量图9　缓和曲线外侧轨道Fig.9 Outside track of ease curve

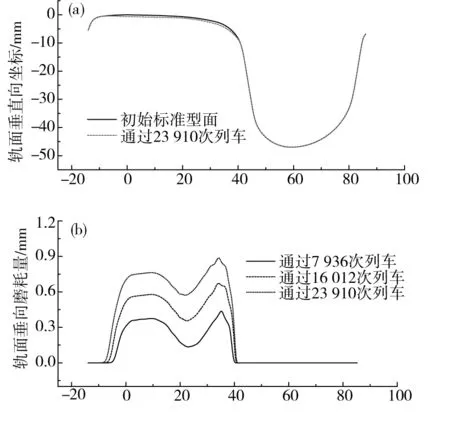
(a)轨道型面变化;(b)轨道累积磨耗量图10　缓和曲线内侧轨道Fig.10 Inner track of ease curve

2.3直线地段

在直线地段上，左右侧轨道的磨耗情况基本相似，主要集中在轨头上，当车辆通过3 333 240次时轨道的磨耗深度为1.57 mm，磨耗量远小于圆曲线和缓和曲线。

图11　直线槽型轨型面变化Fig.11 Profile changes of linear groove track

图12　直线槽型轨型面累积磨耗量Fig.12 Wear of linear groove track

3　结论

1)圆曲线外侧轨道的磨耗主要集中在轨肩处，当列车通过15 404次时最大磨耗量为2.5 mm，随着车辆通过次数的增加槽型轨内侧轨槽发生轻微磨耗；

2)圆曲线内侧轨道，当列车通过次数较少时磨耗主要集中在轨头及轨肩处，随着列车通过次数增加磨耗量变大，轨槽磨耗量与轨头及轨肩的磨耗量基本相当；

3)缓和曲线外侧轨道磨耗主要集中在轨肩列车通过23 910次时最大磨耗量为2.5 mm，内侧轨道磨耗主要集中在轨头及轨肩处但其磨耗深度远小于外侧轨道仅0.88 mm。缓和曲线轨道的磨耗量远小于圆曲线上轨道的磨耗量。

4)在直线地段上，左右侧轨道的磨耗情况基本相似，均主要集中在轨头上，且磨耗量远小于圆曲线和缓和曲线。

[1] 陈鹏.槽型轨及普通钢轨对独立轮对轻轨车辆轮轨动力特性的影响[J].城市轨道交通研究, 2012, 15(2):65-68.

CHEN Peng. Influence of groove rail and general rail on the dynamic characteristics of light rail vehicles with independent wheel set[J]. Urban Mass Transit, 2012, 15(2):65-68.

[2] 占栋, 于龙, 肖建,等. 基于激光摄像技术的钢轨磨耗截面积测量方法研究[J]. 铁道学报, 2014,36(4):32-37.

ZHAN Dong, YU Long, XIAO Jian, et al. Study on track wear cross-section measurement utilizing laser-photogrammetric technique[J]. Journal of the China Railway Society, 2014, 36(4):32-37.

[3] 丁军君, 李芾, 周张义,等. 基于车轮磨耗寿命预测的轨道参数研究[J]. 铁道科学与工程学报, 2013, 10(4):13-18.

DING Junjun, LI Fu, ZHOU Zhangyi, et al. Parametric study of the railway based on wheel wear lifetime prediction[J]. Journal of Railway Science & Engineering, 2013, 10(4):13-18.

[4] Zobory I Z. Prediction of wheel/rail profile wear[J]. Vehicle System Dynamics, 1997, 28(2):221-259.

[5] DING Junjun, LI Fu, HUANG Yunhua, et al. Application of the semi-Hertzian method to the prediction of wheel wear in heavy haul freight car[J]. Wear, 2013, 314(1-2):104-110.

[6] 王璞, 高亮, 蔡小培. 重载铁路钢轨磨耗演变过程的数值模拟[J]. 铁道学报, 2014, 36(10):70-75.

WANG Pu,GAO Liang,CAI Xiaopei. Numerical simulation of rail wear evolution of heavy hual railways[J]. Journal of the China Railway Society, 2014, 36(10):70-75.

[7] Kik W, Piotrowski J. A fast, approximate method to calculate normal load at contact between wheel and rail and creep forces during rolling[C]//2nd Mini Conference on Contact Mechanics and Wear of Rail/Wheel System, TU Budapest, Hungary, 1996: 52-61.

[8] Kovalev R, Lysikov N, Mikheev G, et al. Freight car models and their computer-aided dynamic analysis[J]. Multibody System Dynamics, 2009, 22(4):399-423.

[9] Specht W.New particulars of wear of heavy railway carriage wheels [J]. Glasers Annalen, 1987, 9: 271-280.

[10] WANG P, GAO L. Numerical simulation of wheel wear evolution for heavy haul railway [J]. Journal of Central South University, 2015, 22(1):196-207.

Numerical simulation of groove track wear evolution

YANG yang，LI Fu，ZHANG Maosong，DING Junjun

(School of Mechanical Engineering, Southwest Jiaotong University, Chengdu 610031, China)

This paper adopted the multi-body dynamics analysis software UM to study the wear law of rail. Taking the self-developed 70% low-floor trams as an example, the rail wear calculation model of 59R2 groove was establisked on the basis of the wheel-rail multi-point contact theory. The groove track wear situations at ease curve, circular curve and line area were analyzed. The results show: Wear is focused on rail shoulder at outside track of circular curve. When the trams passed less frequently, the wear is focused on rail head and shoulder at inner track. With the increasing numbers of the trams, the wear of the groove is equaled to that in the rail head and rail shoulder. The amount of wear at ease curve track is much less than that on the circular curve. Outside track’s wear is focused on rail shoulder while inner track’s wear is focused on both rail head and rail shoulder. In straight line, the amount of wear on left and right side is similar and far beyond the wear on ease curve and circular curve.

groove track; low floor rail vehicles; rail wear regular; multi-point contact model;numerical simulation

2015-11-11

国家自然科学基金资助项目(51305359);中央高校基本科研业务费专项资金资助项目(2682014BR020)

李芾(1956-)，男，云南昆明人，教授，博士，从事轨道交通车辆结构及动力学方面研究；E-mail：lifu@home.swjtu.edu.cn

U213.42

A

1672-7029(2016)08-1607-06