不同跨径高铁连续梁桥悬臂施工线形分析研究
2016-09-16杨耀方淑君段传武余豪
杨耀,方淑君,段传武,余豪
(中南大学 土木工程学院,湖南 长沙 410075)
不同跨径高铁连续梁桥悬臂施工线形分析研究
杨耀,方淑君,段传武,余豪
(中南大学 土木工程学院,湖南 长沙 410075)
结合高速铁路中主跨64,80和100 m的3种常见连续梁桥,基于Midas/civil软件平台,采用数值分析方法计算分析了悬臂施工过程不同工况下梁体的变形规律,并与施工过程中的实测值进行对比。研究结果表明:高速铁路连续梁桥刚度较大,活载引起的最大挠度较小,一般在5-15 mm范围;3种跨度连续梁桥的最大施工预拱度在20-30 mm范围,且方向向下;连续梁桥边跨合拢后,边跨向上变形,中跨向下变形;连续梁桥中跨合拢后,边跨向下变形,中跨向上变形;受混凝土收缩徐变的影响,连续梁桥的中跨出现微小的上挠,边跨受影响较小;施工过程中梁体变形实测值与理论值吻合较好,有限元结果能很好地反映梁体变形的实际情况。
高速铁路;连续梁桥;悬臂施工;线形;数值分析
随着铁路工程建设的发展,铁道专项工程的信息化成为现在和将来的发展趋势,铁路信息化是铁路现代化的主要标志,其重要目的是将信息技术广泛应用于铁路生产经营的各项活动中,改造这一传统产业,提高铁路运输生产率和竞争力[1]。连续梁桥线形监控信息化旨在充分利用信息化手段,规范连续梁线形监控量测工作,加强偏差超限控制,实现连续梁线形监控量测信息化,但在此过程中存在一系列有待解决的问题,设计人员对实测数据的分析有限,现场技术人员对梁体变形规律的认知不够等。为了更好推进连续梁桥线形监控信息化,提升设计人员和现场技术人员对连续梁线形变化规律的认知度,不同跨径连续梁桥施工过程中线形变化规律的研究和理论结果具有重要的现实意义。依托于高速铁路中的(40+64+40)m、(48+80+48)m 和(60+100+60)m 3种常见跨度连续梁桥,分别建立Midas有限元模型,结合2座(60+100+60)m连续梁桥的实测数据,从活载挠度、施工预拱度、合拢工况挠度变化和收缩徐变挠度变化4个方面探讨施工过程中梁体线形的变化规律。
1 工程概况
高速铁路(40+64+40) m连续梁桥,中支点截面中心线处梁高6.035 m,跨中10 m直线段及边跨13.75 m直线段截面中心线处梁高3.035 m;高速铁路(48+80+48) m连续梁桥,中支点截面中心线处梁高6.635 m,跨中9m直线段及边跨13.25 m直线段截面中心线处梁高3.835 m;高速铁路(60+100+60) m连续梁桥,中支点截面中心线处梁高7.835 m,跨中10 m直线段及边跨15.75 m直线段截面中心线处梁高4.835 m;梁底下缘按二次抛物线变化,边支座中心线至梁端0.75 m,桥梁宽度为12.6 m,底板宽度6.7 m。
2 梁体变形有限元结果分析
2.1有限元模型
参照时速350 km/h客运专线铁路无砟轨道现浇预应力混凝土连续梁设计图纸,建立3座连续梁桥的有限元模型,如图1所示。模拟施工过程考虑的因素有:结构自重、张拉预应力、收缩徐变、温度变化、临时支撑体系、体系的转换及施工荷载等[2]。连续梁桥采用梁单元来模拟,单元划分考虑到施工节段、变截面、支座等因素;本模型的边界条件采用一般支承+弹性连接模拟;梁段湿重和挂篮自重均采用集中力+集中力偶模拟。

(a)(40+64+40) m连续梁桥;(b)(48+80+48)m 连续梁桥;(c)(60+100+60)m 连续梁桥图1 连续梁桥有限元模型Fig.1 FEM of continuous girder bridges
2.2活载挠度结果
列车竖向静活载采用ZK活载,ZK标准活载如图2所示。

图2 ZK标准活载Fig.2 ZK standard live load
图3为(40+64+40) m连续梁桥、(48+80+48) m连续梁桥、(60+100+60) m连续梁桥活载挠度图[3]。
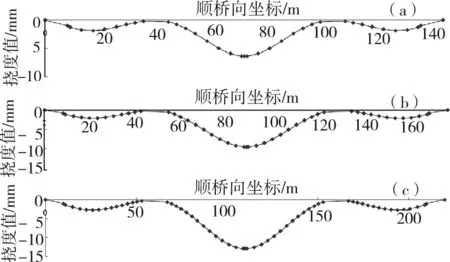
(a)(40+64+40) m连续梁桥;(b)(48+80+48) m 连续梁桥;(c)(60+100+60) m 连续梁桥图3 连续梁桥活载挠度Fig.3 Live-load deflection of continuous girder bridges
由连续梁桥活载挠度图可知,边跨活载挠度远小于中跨活载挠度,这也是很多学者认为边跨设置预拱度时可以不考虑活载的原因。根据Midas活载分析的数值结果,就活载挠度最大值而言,在高铁活载影响下,64 m跨连续梁桥边跨下挠1.83 mm,中跨下挠6.32 mm,中跨挠度是边跨挠度的3.45倍,中跨挠度是跨径的1/10 126;80 m跨连续梁桥边跨下挠2.13 mm,中跨下挠9.60 mm,中跨挠度是边跨挠度的4.5倍,中跨挠度是跨径的1/8 333;100 m跨连续梁桥边跨下挠2.74 mm,中跨下挠12.94 mm,中跨挠度是边跨挠度的4.72倍,中跨挠度是跨径的1/7 728;故高速铁路三跨连续梁桥中跨活载挠度约是边跨活载挠度的3~5倍,约是跨径的1/10 000~1/7 500。上述3种跨度连续梁桥的最大活载挠度分别为6.32,9.60和12.94 mm,相比于公路桥梁,活载挠度较小,说明高速铁路连续梁桥的刚度较大,这是由于在设计时箱梁截面尺寸取值较大,并且预应力钢束设置较多,通过桥梁博士软件估束功能分析,高铁连续梁桥预应力钢束设置数量约是公路桥梁的2倍左右。
2.3施工预拱度结果
施工预拱度考虑梁体自重、挂篮自重、张拉预应力和混凝土收缩徐变的影响,本模型根据设计院要求,施工预拱度不考虑活载的影响。
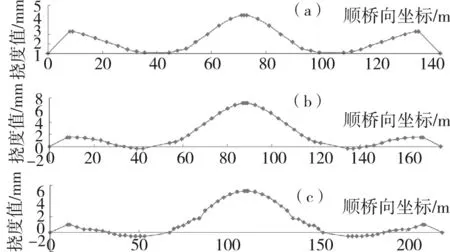
图4分别为(40+64+40) m连续梁桥、(48+80+48) m连续梁桥、(60+100+60) m连续梁桥施工预拱度图[4]。

(a)(40+64+40) m连续梁桥;(b)(48+80+48) m 连续梁桥;(c)(60+100+60) m 连续梁桥图4 连续梁桥施工预拱度Fig.4 Construction camber of continuous girder bridges
由连续梁桥施工预拱度图可知,80 m跨和100 m跨连续梁桥的边跨施工预拱度最大值和中跨施工预拱度最大值大致相当,每个墩身的大里程和小里程悬臂段施工段预拱度也以墩顶对称分布,64 m跨边跨施工预拱度比中跨大。根据Midas施工预拱度分析的数值结果,就施工预拱度最大值而言,64 m跨连续梁桥边跨为-22.7 mm,中跨为-9.6 mm;80 m跨连续梁桥边跨为-23.2 mm,中跨为22.7 mm;100 m跨连续梁桥边跨为23.9 mm,中跨为29.3 mm。上述3种跨度连续梁桥的最大施工预拱度在20~30 mm范围[5,6],相比于公路桥梁,施工预拱度较小,说明高速铁路连续梁桥的刚度较大;并且公路桥梁的施工预拱度一般是向上的,上述高速铁路桥梁施工预拱度是向下的,说明预应力钢束设置较多,使桥梁在施工过程中会有上挠的趋势。
2.4合拢工况挠度结果
边跨合拢施工步骤为:拆除挂篮,安装临时刚性连接构造和水箱,立模浇筑边跨合拢段,边浇筑边放空水箱;混凝土达到设计强度95%后张拉并锚固第1批合拢束和横向预应力束;拆除中墩墩身临时固结,落梁,将中支点水平方向临时约束,张拉第2批合拢束,并压浆封锚。
中跨合拢施工步骤为:安装中跨跨中临时刚性连接构造和水箱,拆除边孔支架和中支点水平方向临时约束;用悬吊支架现浇中跨合拢段,边浇筑边放空水箱;混凝土达到设计强度95%后张拉中跨合拢块顶板预应力束、底板预应力束,并压浆封锚。
图5为(40+64+40)m连续梁桥、(48+80+48)m连续梁桥、(60+100+60)m连续梁桥合拢挠度变化图。

(a)(40+64+40) m连续梁桥;(b)(48+80+48) m 连续梁桥;(c)(60+100+60) m 连续梁桥图5 连续梁桥合拢挠度Fig.5 Closure deflection of continuous girder bridges
由连续梁桥合拢挠度变化图可知,连续梁桥边跨合拢后,边跨向上变形,中跨向下变形[7];边跨合拢后,就梁体变形最大值而言,64 m跨连续梁桥边跨上挠14.2 mm,中跨下挠19.3 mm;80 m跨连续梁桥边跨上挠15.9 mm,中跨下挠14.5 mm;100 m跨连续梁桥边跨上挠18.2 mm,中跨下挠17.4 mm。连续梁桥中跨合拢后,边跨向下变形,中跨向上变形;中跨合拢后,就梁体变形最大值而言,64 m跨连续梁桥边跨下挠6.0 mm,中跨上挠15.5 mm;80 m跨连续梁桥边跨下挠6.4 mm,中跨上挠21.8 mm;100 m跨连续梁桥边跨下挠9.6 mm,中跨上挠31.7 mm。相对于最大悬臂施工状态,中跨合拢后的成桥线形边跨和中跨都是上挠的,不过64 m跨连续梁的中跨挠度变化不大,这与预拱度的大小规律吻合良好。
2.510 a收缩徐变挠度结果
收缩徐变按《公路钢筋混凝土及预应力混凝土桥涵设计规范》(JTG D60—2004)考虑,公路规范JTG D62—2004的徐变系数采用的是欧洲CEB-FIP (1990)中的徐变模型,欧洲CEB-FIP (1990)模型关于收缩应变的计算除了考虑构件尺寸和时间、环境相对湿度、水泥种类外,还考虑了混凝土的极限抗压强度,极限收缩应变则由混凝土轴心抗压强度和相对湿度所确定[5]。
图6为(40+64+40) m连续梁桥、(48+80+48) m连续梁桥、(60+100+60) m连续梁桥10 a收缩徐变挠度变化图。
(a)(40+64+40) m连续梁桥;(b)(48+80+48) m 连续梁桥;(c)(60+100+60) m 连续梁桥图6 连续梁桥收缩徐变挠度Fig.6 Shrinkage and creep deflection of continuous girder bridges
由连续梁桥l0 a收缩徐变挠度图可知,受混凝土收缩徐变的影响,连续梁桥的中跨出现微小的上挠,边跨受影响较小。根据Midas收缩徐变分析的数值结果,就收缩徐变挠度最大值而言,64 m跨连续梁桥边跨为2.3 mm,中跨为4.0 mm;80 m跨连续梁桥边跨为1.5 mm,中跨为7.1 mm;100 m跨连续梁桥边跨为1.0 mm,中跨为5.3 mm。与活载挠度和施工预拱度不同,收缩徐变挠度并不是跨度越大挠度越大,此处是80 m连续梁桥收缩徐变上挠最大[8]。
3 梁体变形实测值与理论值对比分析
为了验证梁体线形变化规律有限元结果的正确性,以京沈客专下桃花吐(60+100+60) m连续梁桥和铁营子(60+100+60) m连续梁桥为例,进行理论值和实测值的对比分析[9]。
3.1悬臂施工状态下变形分析
图7~9分别为(60+100+60) m连续梁桥2号块、5号块和8号块顶板和底板挠度实测值与理论值的对比图,其中“G”代表灌注混凝土施工阶段,“Z”代表张拉预应力施工阶段。
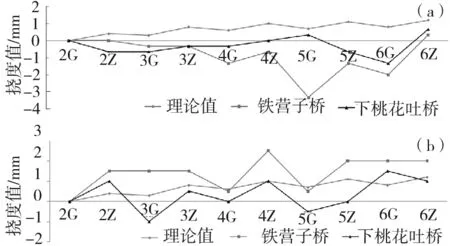
图7 2号块顶板和底板挠度实测值与理论值对比Fig.7 Comparison of measured value and theoretical value for roof and floor plate of block No.2

图8 5号块顶板和底板挠度实测值与理论值对比Fig.8 Comparison of measured value and theoretical value for roof and floor plate of block No.5

图9 8号块顶板和底板挠度实测值与理论值对比Fig.9 Comparison of measured value and theoretical value for roof and floor plate of block No.8
由悬臂施工状态下3个节块的顶板和底板挠度实测值与理论值对比图可知,梁体在预应力张拉后上挠0~6 mm,梁体在灌注混凝土后下挠0~6 mm,并且随着悬臂段的伸长,梁体变形更明显。梁体变形的实测值与理论值差距都在0~4 mm范围,说明理论数据与实测数据较吻合[2,9],并且高铁连续梁桥的刚度较大,所以梁体悬臂施工状态下梁体变形较小。
3.2边跨合拢工况变形分析
图10为2座(60+100+60)m连续梁桥边跨合拢后全桥挠度变化实测值与理论值的对比[10]。

图10 边跨合拢工况挠度实测值与理论值对比Fig.10 Comparison of measured value and theoretical value for deflection of side span closure
由连续梁边跨合拢挠度变化线形可知,铁营子连续梁桥的实测值与理论值吻合较好,说明梁体变形的有限元结果能很好地反映连续梁施工的实际情况。下桃花吐连续梁桥的实测值较理论值小,两座相同跨度连续梁桥的梁体变形有一定的差距,变形最大差距7~10 mm,原因可能是:2座桥的边跨现浇支架形式不同,下桃花吐桥0号块悬臂施工全程设置临时钢管支撑[11],如图11~12所示,导致下桃花吐连续梁桥悬臂长度较小,所以变形较理论值小。

图11 边跨现浇支架对比Fig.11 Comparison of cast-in-place bracket for side span

图12 0号块临时支撑对比Fig.12 Comparison of temporary support for block No.0
3.3中跨合拢工况变形分析
图13为2座(60+100+60) m连续梁桥中跨合拢后全桥挠度变化实测值与理论值的对比图。

图13 中跨合拢工况挠度实测值与理论值对比Fig.13 Comparison of measured value and theoretical value for deflection of midspan closure
由连续梁中跨合拢挠度变化线形可知,2座连续梁桥的实测值与理论值中跨吻合较好,边跨挠度有微小的差距,铁营子连续梁桥边跨变形与理论值最大差距0~5 mm,下桃花吐连续梁桥边跨变形与理论值最大差距0~8 mm。总之,Midas软件计算的梁体变形有限元结果能很好地反映连续梁桥施工的实际情况[12-13]。
4 结论
1)高速铁路三跨连续梁桥刚度较大,活载引起的最大挠度较小,一般在5~15 mm范围,中跨活载挠度约是边跨活载挠度的3~5倍,约是跨径的1/10 000~1/7 500。
2)3种跨度连续梁桥的最大施工预拱度在20~30 mm范围,且方向向下。
3)连续梁桥边跨合拢后,边跨向上变形,中跨向下变形;连续梁桥中跨合拢后,边跨向下变形,中跨向上变形。
4)受混凝土收缩徐变的影响,连续梁桥的中跨出现微小的上挠,边跨受影响较小。
5)梁体变形实测值与理论值吻合较好,说明梁体变形的有限元结果能很好地反映连续梁施工的实际情况。并且施工过程中临时结构的设置会对梁体变形产生影响,如边跨现浇段支架形式和零号块支承情况等。
[1] 周岩,白丽.高速铁路工程建设项目管理信息化的研究[J].铁路计算机应用,2011,20(2):28-34.
ZHOU Yan, BAI Li. Research on informatization of project management for engineering construction of high-speed railway[J]. Railway Compute Application, 2011, 20(2): 28-34.
[2] 盛兴旺,刘海涛.沪宁城际铁路京杭大运河大跨度连续梁施工监控关键技术研究[J].工业建筑,2010,40(10):28-30.
SHENG Xingwang, LIU Haitao. Research on the key technologies of jinghang grand canal continuous beam's construction monitoring on shanghai-nanjing intercity railway[J]. Industrial Construction, 2010, 40(10): 28-30.
[3] 张洲.高速铁路连续梁桥施工控制关健问题研究[D].武汉:武汉理工大学,2010.
ZHANG Zhou. Research on the key technology in construction control of continuous beam bride in high-speed railway[D]. Wuhan: Wuhan University of Technology, 2010.
[4] 陈元清,李小波.温福铁路昆阳特大桥施工控制[J].世界桥梁,2011(3):37-44.
CHEN Yuanqing , LI Xiaobo. Construction control of kunyang bridge on wenzhou-fuzhou railway[J]. World Bridge, 2011(3): 37-44.
[5] 李子龙.(40+64+40)m预应力混凝土连续梁桥施工监控技术研究[D].石家庄:石家庄铁道大学,2014.
LI Zilong. Construction monitor and control technology research of (40 +64 +40) m prestressed concrete continuous girder bridge[J]. Shijiazhuang: Shijiazhuang Tiedao University, 2014.
[6] 沈金贵.时速350 km高速铁路大跨度连续梁悬浇施工监控[J].世界桥梁,2011(1):35-37.
SHEN Jingui. Construction monitoring and control of cantilever casting of long span continuous girder for 350 km/h high-speed railway[J]. World Bridge, 2011 (1): 35-37.
[7] 杨超.预应力混凝土连续( 刚构) 梁桥线形监控探索[J].铁道建筑技术,2013(7):82-86.
YANG Chao. Exploration of linear monitoring of prestressed concrete continuous (rigid frame) beam bridge[J]. Railway Construction Technology, 2013(7):82-86.
[8] 童武元,位东升.虎跳门特大桥施工控制计算分析[J].世界桥梁,2011(1):38-41.
TONG Wuyuan, WEI Dongsheng. Calculation and analysis of construction control of hutiaomen bridge[J]. World Bridge, 2011(1): 38-41.
[9] 李程远,邹颖,郑弋晨.杭长客长某预应力混凝土连续梁桥线形监控[J].施工技术,2013,42(12):5-7.
Li Chengyuan, Zou Ying, Zheng Yichen. Linear control for prestressed concrete continuous girder in hangzhou-changsha passenger dedicated line[J]. Construction Technology,2013,42(12):5-7.
[10] 戴公连,王伟民,刘 柯.基于变形的铁路混凝土连续梁合龙方案比较[J].桥梁建设,2014,14(4):96-101.
Dai Gonglian, WANG Weimin, LIU Ke. Comparison of closure schemes for railway concrete continuous girder based on deformation[J]. Bridge Construction, 2014,14(4):96-101.
[11] 毛新军,宋鹏华.京石铁路客运专线跨青银高速公路连续梁线形控制[J].铁道建筑技术,2011(5):85-88.
Mao Xinjun,Song Penghua. Continuous beam linear control for beijing-shijiazhuang passenger dedicated railway crossing qingdao-yinchuan highway[J]. Railway Construction Technology,2011(5):85-88.
[12] 王常峰,陈兴冲,张文建,等.无砟轨道高速铁路桥梁线形控制技术研究[J].兰州交通大学学报,2010,29(3):12-16.
WANG Changfeng, CHEN Xingchong, ZHANG Wenjian, et al. Research on linear monitoring technology for bridges on ballastless track high-speed railway[J]. Journal of Lanzhou Jiaotong University, 2010,29(3):12-16.
[13] 许交武.武广客运专线罗水大桥施工控制[J].桥梁建设,2011(3):76-80.
XU Jiaowu. Construction Control of luoshui bridge on wuhan-guangzhou passenger dedicated railway[J]. Bridge Construction, 2011(3):76-80.
Linear analysis research on cantilever construction of different spans continuous girder bridge for high-speed railway
YANG Yao,FANG Shujun, DUAN Chuanwu,YU Hao
(School of Civil Engineering , Central South University, Changsha 410075,China)
According to three kinds of common continuous girder bridges with main span of 64, 80 and 100 m in high-speed railway, based on the software platform of Midas/civil, this article calculated and analyzed the deformation variation of beam compared with actual measured values under different conditions during cantilever construction process. The results show that: The maximum deflection caused by live load is small, generally between 5-15 mm, for stiffness of continuous girder bridges is much in high-speed railway. The maximum downward construction camber of three kinds of continuous girder bridges is between 20-30 mm. Side span is upward and midspan is downward after closure construction of side span, and side span is downward and midspan is upward after closure construction of midspan. Because of influence of shrinkage and creep of concrete, there is a tiny scratch for the midspan and is smaller for the side span. In the construction process, the deformation of the beam is in good agreement with the theoretical values and the results of the finite element method can reflect the actual situation of the deformation of the beam.
high-speed railway; continuous girder bridges; cantilever construction;linear; numerical analysis
2015-11-04
国家自然科学基金资助项目(51378504)
方淑君(1974-),女,浙江义乌人,副教授,从事桥梁结构空间分析与极限承载力研究;E-mail:xbyujun@csu.edu.cn
U448.23
A
1672-7029(2016)08-1549-06
