沙尘暴环境对高速铁路挡风墙设置的影响

牛波,杜礼明

(大连交通大学 辽宁省高等学校载运工具先进技术重点实验室，辽宁 大连 116028)



沙尘暴环境对高速铁路挡风墙设置的影响

牛波,杜礼明

(大连交通大学 辽宁省高等学校载运工具先进技术重点实验室，辽宁 大连 116028)

为保证列车在风沙环境下安全运行，需在铁路沿线设置挡风墙。基于欧拉双流体模型和大气底层边界速度型风场模型，通过数值模拟方法研究高速列车在不同车速和不同沙尘暴等级下运行时，沙尘对挡风墙高度和距离等参数的影响。研究结果表明：与在单纯大风环境下运行相比，列车在沙尘暴环境下运行时所受气动力有所不同：考虑沙尘的影响后，列车整车倾覆力矩有所增加。为此，在研究挡风墙的设置时，应考虑沙尘的影响。在沙尘暴环境下，挡风墙的最优高度应有所增加；当挡风墙距离一定时，挡风墙的最优高度随着列车运行速度提高而增大，随着沙尘暴等级的提高而降低；挡风墙高度一定时，挡风墙的最优距离随着列车运行速度提高而减少，随着沙尘暴等级的提高而增加；挡风墙最优距离和高度近似成二次多项式关系。

铁路工程；挡风墙；数值模拟；高速列车；沙尘暴

高速列车在行驶过程中，若受到强横风的作用，列车的气动性能便会迅速恶化[1-2]，尤其是在风沙环境下，横风将会严重影响旅客乘坐舒适性并对运行安全造成严重影响[3-6]。为减少事故的发生，降低横风对列车安全运行的影响，可在风区铁路沿线建造挡风墙[7-9]。目前，对于挡风墙的研究大致分3类：挡风墙高度，挡风墙至轨道中心线距离和挡风墙的结构外形设计。刘凤华[10]分析了4种不同类型的挡风墙对列车的安全防护效果评价；李燕飞等[11]对高速铁路开孔式挡风墙外形进行了优化研究；叶坤等[12]对在横风作用下高速铁路挡风墙进行了高度和位置的优化分析；杨斌等[13]针对大风区不同路况下的挡风墙提出了合理高度；姜翠香等[14]研究了在横风环境下挡风墙高度和设置位置对一线、二线棚车气动性能的影响。但目前的研究仅考虑了在大风环境下挡风墙的设计对列车气动性能的影响。实际上，风沙总是伴随出现的，尤其是在我国的内蒙古和新疆等强风沙地区[15]。因此，单纯研究风的影响既不能真实地揭示风沙对列车运行的平稳性和安全性影响，也不能体现出挡风墙的作用，也就不能很好地指导挡风墙的结构设计。通过欧拉双流体模型模拟风沙两相流，使用大气底层边界速度型风场模拟自然风，分析沙尘暴环境下挡风墙高度和距离对列车横向气动力矩的影响规律，以获得挡风墙的最佳高度和最优距离的关系，为高速铁路挡风墙的设置参数提供参考依据。

1　计算模型及方法

1.1计算模型与数值方法

以某高速动车组的几何尺寸为原型建立数值计算模型，由于列车中部的气动力变化已经趋于稳定[16]，因此可将列车模型简化为头车、中间车和尾车3辆车编组，其长度分别为25.8 ,24.8和25.8 m，列车的宽度为3.2 m，高度为3.89 m。同时，将列车简化为一个光滑曲面的几何体，并忽略转向架、受电弓及门把手等细部特征[17]。

采用直立式挡风墙，其高度定义为路堤上部至挡风墙顶部的距离，距离定义为挡风墙内侧表面至一线轨道中心线的距离，挡风墙厚度为1.2 m，路堤高度为5 m，坡脚角度为1∶1.5[13]。

沙尘运动为两相流运动，欧拉双流体模型将空气与运动沙尘均看作是流体，认为二者之间相互贯穿渗透，用体积分数来描述每一相的存在，这样可以有效避免沙尘颗粒数目的限制，节省计算资源，提高计算效率[19]。故采用该模型，并选定空气为第一相，沙粒为第二相。按照《沙尘暴天气等级》的规定，并选取沙尘暴S3，强沙尘暴S4和特强沙尘暴S5 3个等级进行研究，相关参数如表1所示。

表1　风沙计算参数

沙尘暴中的风和沙往往不是就地产生的，因此，采用更接近实际情况的大气底层边界速度型风场来模拟自然风[20]，风速在大气边界层高度的方向上以指数形式增加。数值模拟软件采用商用计算流体动力学软Fluent进行数值模拟。边界层使用标准壁面函数，并采用定常可压缩的N-S方程和标准κ-ε两方程湍流模型，耦合压力与速度使用SIMPLE算法，并使用二阶迎风格式进行离散。

1.2计算域及网格划分

考虑到气流的绕流和流场的充分发展，选择长、宽、高为320 m×100 m×40 m的长方体为计算区域。计算区域如图1所示。

为保证模拟计算的准确性和计算效率，需将车体和挡风墙周围网格划分的较密，而远离车体的外流场网格可以较疏[21]，因此采用尺寸函数的方法来划分网格，划分后的网格数量为250万，最终得到计算域的网格如图2所示。

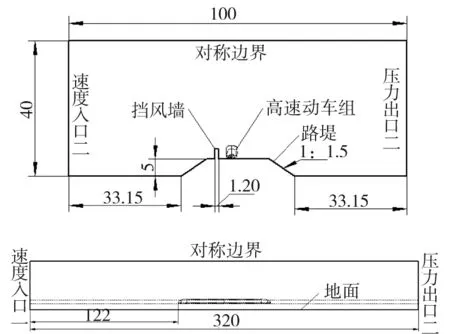
(a)正视图；(b)侧视图单位：m图1　计算区域及尺寸Fig.1 Computational domain and size

图2　计算域网格Fig.2 The grids of calculation field

1.3边界条件及计算工况

1)流动入口1。入口1设置为含有沙粒的均匀风场，风速和沙粒的流入速度均为列车速度，方向与车速相反，并且还需根据工况设定沙粒的直径、体积浓度等参数。

2)流动入口2。入口2设置为含有沙粒的大气底层边界速度型风场，速度随高度的变化规律为vy=vy10﹒(y/y10)0.16，其中y10=10 m，vy10为y=10 m处的横风速度。同样，还需设定沙粒直径、体积浓度等参数。

3)计算域流动出口。出口1和出口2均使用压力出口边界条件。

4)地面、路堤及挡风墙。由于地面、路堤及挡风墙与列车之间存在相对运动，故将三者设定为滑移壁面，移动速度与车速大小相同，方向相反[22]。

5)列车表面和计算域上表面。按照无滑移壁面条件设定。

分别选取列车速度为200，275和350 km/h；挡风墙的高度为2.0，2.5，3.0，3.5，4.0，4.5以及5 m；挡风墙的距离为3.5，3.8，4.2和4.5 m。具体计算工况如表2所示。

表2　计算工况

2　结果与分析

2.1沙尘对铁路挡风墙结构的影响

车速为275 km/h，横风速度为25 m/s，挡风墙高度为4 m，挡风墙距离为4.2 m时，无沙尘和有沙尘(沙尘浓度为4.0×10-8)2种工况下，列车表面的压力分布云图，如图3。

由图可知，在沙尘暴环境下列车表面的压力均有所增加，尤其是列车迎风侧上部压力增加明显。无沙尘工况下，列车整车倾覆力矩为0.169 kN·m；有沙尘工况下，列车整车倾覆力矩为2.812 kN·m。考虑了沙尘的影响后，列车整车倾覆力矩增加了2.643 kN·m。这是由于与无沙尘情况相比，沙尘环境下单位空间体积内所含物质的运动动能增加，当含有沙尘的大风与列车发生相互作用时，列车所受载荷增加，又由于挡风墙的存在改变了流体运动的路径，导致列车迎风侧上部所受压力增加明显，而列车背风侧的压力变化不大，使得列车所受的倾覆力矩增加，列车向背离挡风墙方向扭转的趋势增加。因此，考虑到沙尘影响，挡风墙高度应适当增加。由于在沙尘环境和无沙尘环境下，列车在运行过程中所受的气动力是不同的，所以在研究挡风墙设置参数时，有必要考虑沙尘暴环境对列车产生的影响。

(a)无沙尘工况;(b)有沙尘工况图3　无沙尘和有沙尘工况下列车车身的压力云图Fig.3 Pressure distribution on the surface of the train in wind with sand and without sand

2.2不同挡风墙设置对列车外流场的影响

以下分析沙尘暴环境下挡风墙对列车外流场的影响。横风作用下列车的稳定性主要取决于倾覆力矩[23]。图4为在特强沙尘暴环境下，车速为200 km/h，挡风墙距离为3.8 m时，不同高度挡风墙的条件下中间车车体的压力云图。

挡风墙高度为2.5 m时，车体迎风面为正压区，由于车顶空气流速加快，故出现负压区，背风面上方为负压区，车体向远离挡风墙的方向扭转。挡风墙高度为3.5 m时，车体迎风侧和背风侧均出现负压，但两侧压差不大，车体逐渐开始向挡风墙方向扭转。挡风墙高度为4.5 m时，车体迎风面负压区加剧，而背风面变化不大，两侧压差明显增加，车体朝挡风墙方向扭转的情况加剧。与只考虑横风情况的文献[12]相比，具有类似的结论：随着挡风墙高度的增加，车体逐渐从远离挡风墙方向扭转变为朝挡风墙方向扭转。

图5为在特强沙尘暴环境下，车速为200 km/h，挡风墙高度为3.8 m时，不同挡风墙距离的条件下中间车车体的压力云图。挡风墙距离为3.5 m时，车体迎风面压力在-700～-400 Pa范围内，背风面压力在-400～-100 Pa范围内，在两侧压差的作用下车体向挡风墙方向扭转，随着车体逐渐远离挡风墙，迎风面压力迅速减小，而车体背风面的压力变化不大，当距离为4.2 m时，车体两侧的压力差趋近于0。随着挡风墙距离的增加，车体逐渐从朝挡风墙方向扭转变为背离挡风墙方向扭转。只考虑横风情况的文献[12]也有相同结论。

(a)挡风墙高2.5 m；(b)挡风墙高3.5 m；(c)挡风墙高4.5 m图4　不同高度挡风墙中间车体周围的压力云图Fig.4 Distribution of pressure around the middle coach under different heights of wind-break wall

由此可见，当挡风墙处于某一高度时，会使车体两侧的气压差趋于0，这一高度可确定为这一工况下的最佳高度。同理，把挡风墙设置在某一距离时，车体两侧的气压差也会趋近于0，这一距离可确定为最佳距离。

(a)挡风墙距离3.5m；(b)挡风墙距离3.8 m；(c)挡风墙距离4.2 m图5　不同挡风墙距离中间车体周围的压力云图Fig.5 Distribution of pressure around the middle coach under different distances of wind-break wall

2.3运行速度对最优挡风墙高度和距离的影响

列车运行的稳定性与其受到的倾覆力矩密切相关[24]。气动力和气动力矩的作用点一般与车辆的重心位置并不重合，作用点受车辆的形状、大小和环境风的方向等因素影响。气动力矩的简化中心定为距路堤高度为1.95 m的车体中心位置。倾覆力矩为正值时表示气动力使列车朝远离挡风墙的方向扭转，倾覆力矩为负值时表示气动力使列车向挡风墙方向扭转。

在特强沙尘暴环境下，列车以不同速度行驶情况下列车倾覆力矩随挡风墙高度和距离的变化规律见图6～8，分别分析头、中、尾车的倾覆力矩，选择绝对值最小的倾覆力矩所对应的挡风墙高度和距离则为最优方案。

当挡风墙距离一定时，头车、中间车和尾车的倾覆力矩均随着挡风墙高度的增加而逐渐减小。挡风墙高度较低时倾覆力矩为正值，列车绕着气动中心向背风侧转动；当到达某一高度时倾覆力矩降为0；当挡风墙高度继续增加时，倾覆力矩为负值，列车绕着气动中心向迎风侧转动。倾覆力矩为0时所对应的高度为最优高度。随着挡风墙距离的增加，头车、中间车和尾车的最优高度也逐渐增加，距离过小，倾覆力矩为负值，列车会向迎风侧转动；距离过大，倾覆力矩为正值，列车会向背风侧转动。

表3为在不同车速下，挡风墙距离在3.5～4.5 m时，头车、中间车和尾车挡风墙高度的最优值。

表3　在不同车速下挡风墙的最优高度

由表3可知，随着列车运行速度的提高，挡风墙的最优高度也逐渐增大，车速从200 km/h提升至275 km/h时，挡风墙的最优高度增加了0.29 m，车速从275 km/h提升到350 km/h时，挡风墙的最优高度增加了0.24 m。当列车以一定速度行驶时，如果实际的挡风墙高度低于最优值，列车可以通过降速来使其达到最优行驶条件，如果实际的挡风墙高度高于最优值时，列车可以通过提速来达到最优行驶条件。

(a)头车；(b) 中间车；(c)尾车图6　列车行驶速度为200 km/h倾覆力矩随挡风墙高度和距离的变化规律Fig.6 Capsizing moments changing with the height and the distance of wind-break wall at the speed of 200 km/h

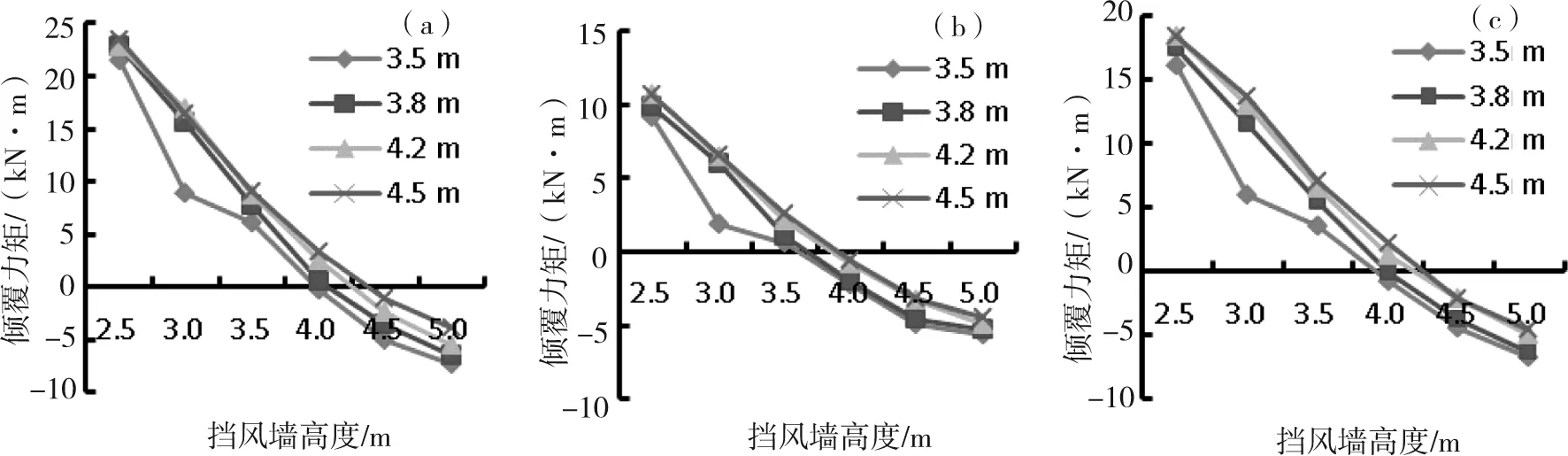
(a)头车；(b) 中间车；(c)尾车图7　列车行驶速度为275 km/h倾覆力矩随挡风墙高度和距离的变化规律Fig.7 Capsizing moments changing with the height and the distance of wind-break wall at the speed of 275 km/h

(a)头车；(b) 中间车；(c)尾车图8　列车行驶速度为350 km/h倾覆力矩随挡风墙高度和距离的变化规律Fig.8 Capsizing moments changing with the height and the distance of wind-break wall at the speed of 350 km/h

2.4不同沙尘暴等级下最优挡风墙高度和距离

列车速度为275 km/h时，在不同沙尘暴等级情况下列车倾覆力矩随挡风墙高度和距离的变化规律见图7，图9和图10，分别分析头、中、尾车的倾覆力矩，选择绝对值最小的倾覆力矩所对应的挡风墙高度和距离则为最优方案。

特强沙尘暴环境下倾覆力矩随挡风墙高度和距离的变化规律见图7。

(a)头车；(b) 中间车；(c)尾车图9　沙尘暴环境下倾覆力矩随挡风墙高度和距离的变化规律Fig.9 Capsizing moment changed with the height and the distance of wind-break wall in a sandstorm

(a)头车；(b) 中间车；(c)尾车图10　强沙尘暴环境下倾覆力矩随挡风墙高度和距离的变化规律Fig.10 Capsizing moment changed with the height and the distance of wind-break wall in a strong sandstorm

Table 4 Optimal heights and distances of wind-break wall in different levels of sandstorm

挡风墙距离/m沙尘暴等级头车最优/m中间车最优/m尾车最优m综合最优/mS34.304.434.103.5S44.144.183.854.14S53.983.913.61S34.444.524.263.8S44.274.283.954.27S54.073.993.67S34.634.804.454.2S44.424.494.164.42S54.254.183.86S34.844.854.554.5S44.524.524.244.52S54.374.253.90

最优方案见表4。固定车速下挡风墙距离一定时，头车、中间车和尾车所确定的挡风墙最优高度均随着沙尘暴等级的提高而降低。文献[12-13]在考虑横风风速对车体倾覆力矩的影响时也得出了类似的结论:随着横风风速的增加，挡风墙的最优高度是减小的。在某种沙尘环境下，头车、中间车和尾车所确定的挡风墙最优高度均随着挡风墙距离的增加而增加。

综合在各种沙尘环境下3节车的最优值，车速为275 km/h情况下挡风墙位置分别为3.5，3.8，4.2和4.5 m时对应的最优高度分别是4.14，4.27，4.42和4.52 m。对这几对数据进行拟合，得到拟合曲线及相应的函数关系。挡风墙最优距离和高度近似成二次多项式关系。经验证，其他的挡风墙高度和距离最优组合点均在该拟合曲线附近。

同理可得到车速为200 km/h和350 km/h的拟合曲线，如图11所示。

图11　挡风墙最优高度和最优距离的拟合曲线Fig.11 Fitted curves of optimal heights and distances of wind-break wall

可见挡风墙最优高度和距离近似成二次多项式关系。当车速增加或降低时，最优挡风墙的高度也要适当增加或降低。综合挡风墙最优高度、最优距离和车速之间的关系，得到表达式：

h=1.424+1.282×10-2v-0.173 3d-2.147×

10-5v2+8.002×10-4vd+0.050 61d2

(1)

式中:h为最优挡风墙高度，m；v是车速，km/h；d为最优挡风墙距离,m。

车速200 km/h及挡风墙的距离为5.7 m时，根据式(1)可得到最优挡风墙高度为4.70 m，而文献[13]未考虑沙尘影响下得到挡风墙合理高度为4.0 ～4.5 m时可保证列车安全运行(环境风速小于25 m/s)。由此可见，在沙尘暴环境下挡风墙的最优高度应有所增加。

3　结论

1)在沙尘环境和无沙尘环境下，列车在运行过程中所受的气动力有所不同，在研究挡风墙设置参数时，有必要考虑沙尘环境对列车产生的影响。在沙尘暴环境下，挡风墙的最优高度应有所增加。

2)挡风墙距离固定时，随着挡风墙高度的逐渐增加，列车由向背风侧转动变为向迎风侧转动；挡风墙高度固定时，随着挡风墙距离的逐渐增加，列车由向迎风侧转动变为向背风侧转动。

3)挡风墙高度一定时，随着列车运行速度的提高，挡风墙的最优距离减少，随着沙尘暴等级的提高，挡风墙的最优距离增加。

4)挡风墙距离一定时，随着列车运行速度的提高，挡风墙的最优高度增大，而随着沙尘暴等级的提高，挡风墙的最优高度降低。

5)固定车速下，挡风墙最优高度和距离近似成二次多项式关系。拟合最优高度、最优距离和车速之间的关系，得到表达式：

h=1.424+1.282×10-2v-0.173 3d-2.147×

10-5v2+8.002×10-4vd+0.050 61d2

[1] Suzuki M,Tannemoto K,Maeda T. Aerodynamics characteristics of train/vehicles under cross wind[J].Journal of Wind Engineering and Industrial Aerodynamics,2003,91(1):209-218.

[2] 黄尊地,常宁. 强侧风不同挡风墙下棚车气动性能[J].铁道科学与工程学报,2012,9(4):101-105.

HUANG Zundi, CHANG Ning. Aerodynamic forces acting on a box car running on the railway alone with the wind-break wall under strong cross-wind[J]. Journal of Railway Science and Engineering, 2012,9(4):101-105.

[3] 刘凤华. 加筋土式挡风墙优化研究[J].铁道工程学报,2006,1(2):96-99.

LIU Fenghua. Study on the optimization of wind-break wall of the reinforced concrete shaped type[J]. Journal of Railway Engineering Society, 2006,1(2):96-99.

[4] Diedrichs B. Studies of two aerodynamics effects on high-speed trains: cross wind stability and discomforting car body vibrations inside tunnels[D]. Stockholm: Royal Institute of Technology,2006.

[5] Andersson, Häggström J, Sima M, et al. Assessment of train-overturning risk due to strong cross-wind[J]. Journal of Rail and Rapid Transit, 2004,218(3):213-223.

[6] Diedrichs B, Sima M,Orellano A, et al. Cross wind stability of a high-speed train on a high embankment[J]. Journal of Rail and Rapid Transit, 2007,221(2):205-225.

[7] Imai T,Fuii T,Tanemoto K, et al. New train regulation method based on wind direction and velocity of natural wind against strong winds[J]. Journal of Wind Engineering and Industrial Aerodynamics,2002,90 (12/13/14/15):1601-1610.

[8] Fufii T, Maeda T,Ishida H, et al. Wind-induced accidents of train/vehicles and their measures in Japan[J]. Quarterly Report of Railway Technical Research Institude,1999,40(1):50-55.

[9] Bettle J,Hollloway A G L, Venart J E S. A computational study of the aerodynamic forces acting on a tractor trailer vehicle on a bridge in cross-wind[J]. Journal of Wind Engineering and Industrial Aerodynamics,2003:91(5):573-592.

[10] 刘凤华.不同类型挡风墙对列车运行安全防护效果的影响[J].中南大学学报:自然科学版,2006,37(1):176-182.

LIU Fenghua. Wind-proof effect of different kinds of wind-break walls on the security of trains[J]. Journal of Central South University: Science and Technology, 2006,37(1):176-182.

[11] 李燕飞,田红旗,刘辉.高速铁路开孔式挡风墙外形优化研究[J].中南大学学报(自然科学版),2011,42(10):3207-3212.

LI Yanfei, TIAN Hongqi, LIU Hui. Optimization of windbreak wall with holes in high-speed railway[J]. Journal of Central South University (Science and Technology), 2011,42(10):3207-3212.

[12] 叶坤,李人宪.高速铁路挡风墙高度和距离优化分析[J].西南交通大学学报,2014,49(2):240-246.

YE Kun, LI Renxian. Optimization analysis of height and distance of shelter wind wall for high-speed railway[J]. Journal of Southwest Jiaotong University, 2014,49(2):240-246.

[13] 杨斌,刘堂红,杨明智.大风区铁路挡风墙合理设置[J].铁道科学与工程学报,2011,8(3):67-72.

YANG Bin, LIU Tanghong, YANG Mingzhi. Reasonable setting of wind-break wall on railway in strong wind areas[J]. Journal of Railway Science and Engineering,2011,8(3):62-72.

[14] 姜翠香,梁习锋. 挡风墙高度和设置位置对车辆气动性能的影响[J].中国铁道科学,2006,27(2):66-70.

JIANG Guixiang, LIANG Xifeng. Effect of the vehicle aerodynamic performance caused by the height and position of wind-break wall[J]. China Railway Science,2006,27(2):66-70.

[15] 张军平,王引生,蒋富强.兰新铁路戈壁地区路基周围风沙流运动特征数值分析[J].中国铁道科学,2011,32(4):14-18.

ZHANG Junping, WANG Yinsheng, JIANG Fuqiang. Numerical analysis on the features of sand flow movement around the emban kment of Lan-Xin Railway in gobi region[J]. China Railway Science,2011,32(4):14-18.

[16] LIU Tanghong, ZHANG Jie. Effect of landform on aerodynamic performance of high-speed trains in cutting under cross wind[J]. Journal of Central South University,2013,20(3):830-836.

[17] 于梦阁,张继业,张卫华. 侧风下高速列车车体与轮对的运行姿态[J].交通运输工程学报, 2011,11(4):48-55.

YU Mengge, ZHANG Jiye, ZHANG Weihua. Running attitudes of car body and wheelset for high-speed train under cross wind[J]. Journal of Traffic and Transportation Engineering,2011,11(4):48-55.

[18] 李田,张继业,张卫华.沙尘暴环境下的高速列车运行安全分析[J].四川大学学报(工程科学版), 2012.44(12):5-8.

LI Tian, ZHANG Jiye, ZHANG Weihua. Running safety analysis of a high-speed train under sandstorm environment[J].Journal of Sichuan University (Engineering Science Edition),2012.44(12):5-8.

[19] 毛军, 郗艳红,杨国伟.侧风风场特征对高速列车气动性能作用的研究[J]. 铁道学报, 2011,33(4):22-30.

MAO Jun, XI Yanhong, YANG Guowei. Research on influence of characteristics of cross wind field on aerodynamic performance of a high-speed train[J]. Journal of the China Railway Society, 2011,33(4):22-30.

[20] Baker C J, Jones J, Lopez C F, et al. Measurements of the cross wind forces on trains[J]. Journal of Wind Engineering and Industrial Aerodynamics,2004,92(7-8):547-563.

[21] 刘珍,张健,杨明智,等. 兰新铁路现有土堤式挡风墙局部加高优化[J].铁道科学与工程学报,2012,9(2):101-106.

LIU Zhen, ZHANG Jian, YANG Mingzhi, et al. The partial raises optimization of existed earth type wind barrier in Lanxin Railway[J]. Journal of Railway Science and Engineering,2012,9(2):101-106.

[22] 程建军,庞巧东. 戈壁强风区挡风构筑物限制下列车动力学特性分析[J].铁道标准设计,2013(1):1-5.

CHENG Jianjun, PANG Qiaodong. Analysis on train aerodynamics characteristics under different types of wind break structures at strong wind zone in gobi[J]. Railway Standard Design,2013(1):1-5.

[23] Carrarini A. Reliability based analysis of the crosswind stability of railway vehicles[J]. Journal of Wind Engineering and Industrial Aerodynamics, 2007,95(7):493-509.

Influence of sandstorms on the setting of wind-break wall of high-speed railway

NIU Bo, DU Liming

(Province Key Lab of Vehicle Engineering Advanced Technology, Dalian Jiaotong University,Dalian 116028, China)

Sandstorm has a serious influence on the safe operation of a train. In order to ensure the safety, wind-break wall is a necessary measure. Based on the Eulerian two-fluid model and the lower atmospheric boundary layer crosswind model, a numerical simulation method was used to stimulate how sandstorms impacted on the setting of wind-break wall, such as the height and the distance, when a high-speed train traveled at different speeds and under different levels of sandstorms. The results show as follows: compared with only wind conditions, aerodynamic forces of a train affected by sandstorms are different, after considering the effect of sand, overturning moment increases. Therefore the effect of sandstorms should be considered in the research. Optimal height should be increased after consideration of it. When the distance is settled, the train turns from leeward side to windward side as the wall’s height increases. When the height is settled, the train turns from windward side to leeward side with the increase of the wall’s distance. When the distance is settled, the optimal height of the wind-break wall increases with the increased speed of the train, but decreases with the increased levels of sandstorm. When the height is settled, the optimal distance increases with the increased speed of the train, but decreases with the increased levels of sandstorm. And there is a quadratic relationship between the optimal heights and distances of wind-break wall.

railway engineering; wind-break wall; numerical simulation ;high-speed train; sandstorm

2016-03-29

国家自然科学基金资助项目(11202043)

杜礼明(1972-)，男，湖北黄冈人，教授，博士，从事机车车辆流体动力学研究：E-mail:dulm@vip.sina.com

U216.413；U271.91

A

1672-7029(2016)08-1457-09