Growth Theorem and Distortion Theorem for a Subclass of Parabolic Starlike Mappings

ZHANG Xiao-fei，YAN Chun-yan

（1.College of Mathematics and Information Science，Pingdingshan University，Pingdingshan 467000，China；2.Department of Information Engineering，Xuchang Vocational Technical College，Xuchang 461000，China）



Growth Theorem and Distortion Theorem for a Subclass of Parabolic Starlike Mappings

ZHANG Xiao-fei1，YAN Chun-yan2

（1.College of Mathematics and Information Science，Pingdingshan University，Pingdingshan 467000，China；2.Department of Information Engineering，Xuchang Vocational Technical College，Xuchang 461000，China）

In this article，we firstly introduce a subclass of parabolic starlike mappings writen as PS（β；ρ）.Secondly，the growth theorem for PS（β；ρ）on the unit ball in complex Banach space is obtained.Finaly，as the application of the growth theorem of PS（β；ρ），the distortion theorem along a unit direction is also established.

parabolic starlike mappings；growth theorem；distortion theorem

2000 MR Subject Classification：32A30，30C45

Article ID：1002—0462（2016）02—0211—10 Chin.Quart.J.of Math. 2016，31（2）：211—220

§1.Introduction

In 1993，Rφnning［1］gave the notion of parabolic starlike functions f.These functions werecharacterized by the fact that the quantity lying in a given parabolic region in the right half-plane.Later，Ali［2］introduced the definition of parabolic starlike functions of order ρ that is contained in the larger class of starlike functions of order ρ.At the same time，he established the sharp growth，covering and distortion theorems for this class of biholomorphic functions.As a direct generalization of parabolic starlike functions of order ρ on the unit disk U=｛ξ：|ξ|＜1｝，Hamada，Honda and Kohr［3］obtained sharp growth and covering theorems for parabolic starlike mappings of order ρ on Bn=｛z∈Cn：‖z‖＜1｝（see also［4］）.In thispaper，we continue the investigation of this generalized class but under a slight modification for the definition and introduce a new parameter in several complex variables.

In the following，we will give some notation and definitions.Let C be the complex plane and Ur=｛ξ∈C：|ξ|＜r｝.The unit disk in C is denoted by U.Let Cnbe the space of n complex variables z=（z1,···,zn）0with the Euclidean inner productand the Euclidean norm‖z‖=〈z,z〉12，where z,w∈Cnand the symbol“0”means transpose.The unit ball Bn=｛z∈Cn：‖z‖＜1｝.Let X denote the complex Banach space with norm‖·‖，B=｛x∈X：‖x‖＜1｝be the unit ball in X.Let Ω be a domain in X，f：Ω→X，for any x∈Ω，if there is a linear mapping Df（x）from X to X such that

then f is said to be holomorphic on Ω.The linear map Df（x）is called the Fr´echet derivative of f at x.In Cn，Df（x）is the Jacobian，always written by Jf（z）.Let f：Ω→X be a holomorphic mapping，if its Fr´echet derivative Df（x）is nonsingular at each x∈Ω，then f is said to be locally biholomorphic on Ω.If the inverse f-1exists and it is holomorphic on the open set f（Ω），then f is said to be biholomorphic.If f（0）=0 and Df（0）=I，then f is called normalized，where I is the identity operator.

We denote by Txthe continuous linear functional on X such that‖Tx‖≤1 and Tx（x）=‖x‖，∀x∈X.By Hahn-Banach theorem，Txalways exists but is not unique in general.For any fixed x∈X，α∈C｛0｝，becausewe getIn particular，Trx=Txwhen r＞0.

Definition 1Let f be a normalized biholomorphic function on the unit diskU and let

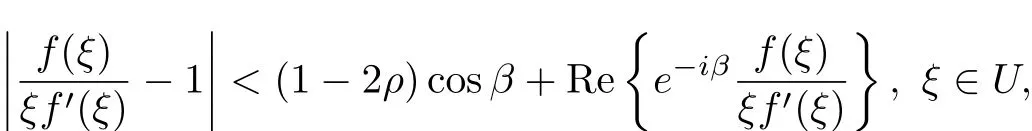
then we say f∈PS1（β；ρ）.

The above definition is the definition of parabolic starlike functions of order ρ which was originally introduced by Ali［2］when β=0.

If f∈PS1（β；ρ），then

is a function from U onto the parabolic domain Ωβ,ρ，where

In the case β=0，we know that

is a biholomorphic function from U onto the parabolic region Ωρin the right half-plane，where

In several complex variables，the subclass of normalized biholomorphic mappings PS（β；ρ） consisting of mappings f：B→X such that.We state the relation in the definition below.

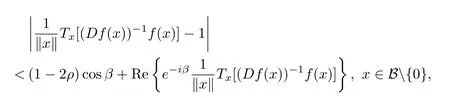
then we say f∈PS（β；ρ）.

By the geometrical meaning of the above definition，we get

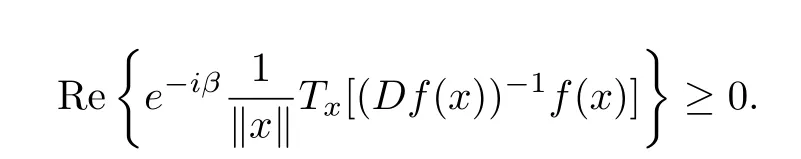
Thus it is that f is also a normalized biholomorphic spirallike mapping of type β.Definition 2 is the definiton of parabolic starlike mappings of order ρ which was defined by Zhang and Feng［4］when β=0.Compared with the definition of parabolic spirallike mappings of type β and order ρ in［5］，Definition 2 is more reasonable.

Definition 3［6］Let f and g be holomorphic function on U.If there is a Schwarz function ω on U such that f（ξ）=g（ω（ξ）），then we say f is subordinate to g.In particular，if g is also univalent on U，then f（ξ）≺g（ξ）is equivalent to f（0）=g（0）and f（U）⊂g（U）.

§2.The Growth Theorem for PS（β；ρ）

In the complex plane，the following growth theorem for normalized biholomorphic functions was well-known.

Theorem A［7］Let f be a normalized biholomorphic function on the unit diskU=｛ζ∈C：|ζ|＜1｝，then

It is natural to extend the above beautiful results to higher dimensions.However，H Cartan［8］pointed out the above theorem for normalized biholomorphic mappings would not hold in several complex variables.And he also suggested to study the starlike mappings and convex mappings as appropriate topics for generalization.Hence，to characterize the growth theorem for subclasses of normalized biholomormic mappings，which has obvious geometrical meaning，is an important work in several complex variables.However，until to Barnard，FitzGeral andGong［9］firstly established the growth andtheorems of starlike mappings on the unit ball Bnin the Euclidean space，there is little result in this field.

Theorem B［9］be normalized biholomorphic starlike mapping.Then

And after that，a lot of researches came to study the growth theorem for starlike mappings and convex mappings on different domain，the reader can consult［10-15］.

In the following，the harnack inequality for PS（β；ρ）is given firstly（see Lemma 3）.Secondly，as the application of Lemma 3，we obtain the growth theorem for PS（β；ρ）（see Theorem 1）.

Lemma 1［15］Suppose that）and fis a spirallike mapping of type β.Let x∈B｛0｝，and let x（t）=f-1（exp（-e-iβt）f（x））（0≤t＜+∞），then

（i）‖x（t）‖is a strictly monotone decreasing function on［0,∞）；

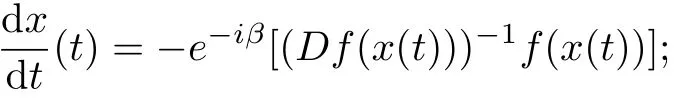
Lemma 2［15］Let x：［0,1］→X be differentiable at the point s∈（0,1］and‖x（t）‖be also differentiable at the point s with respect to t.Then

Lemma 3Suppose that f is a normalized biholomorphic mapping on the unit ball B with f∈PS（β；ρ）,where ρ∈［0,1）,）.Then for all x∈B，

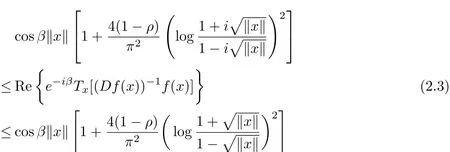
and

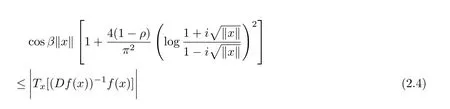
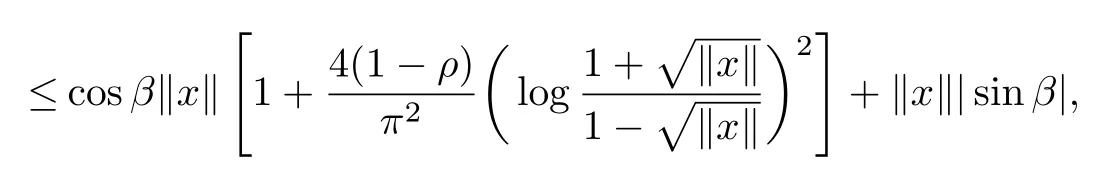
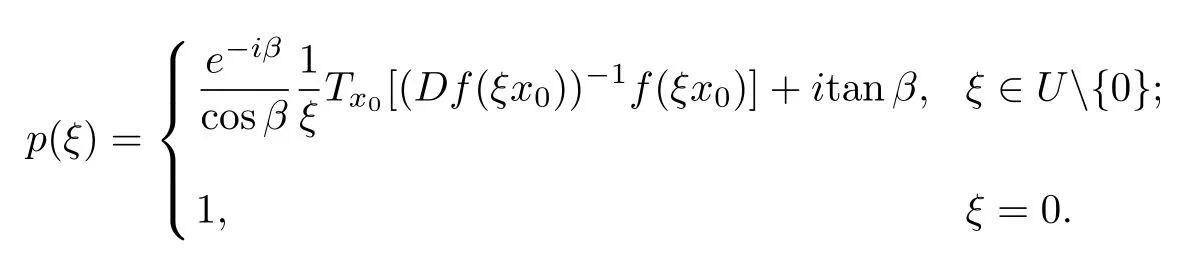
Since

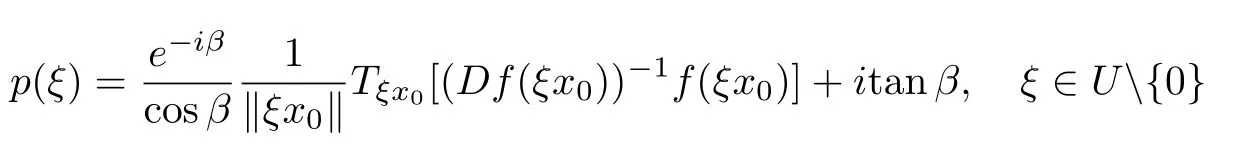
and

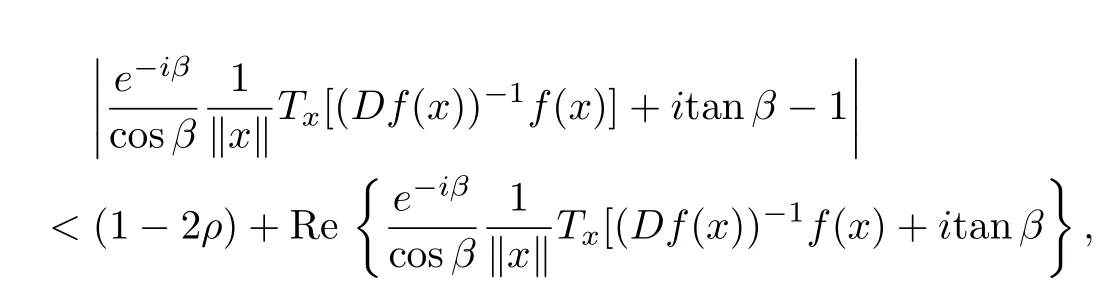
we have

Obviously，the inequality（2.5）holds for all ξ∈U.Hence p（ξ）≺g（ξ），whereg（ξ）=.So，by maximum and minimum principles for harmonic functions we have for all ξ∈U holds

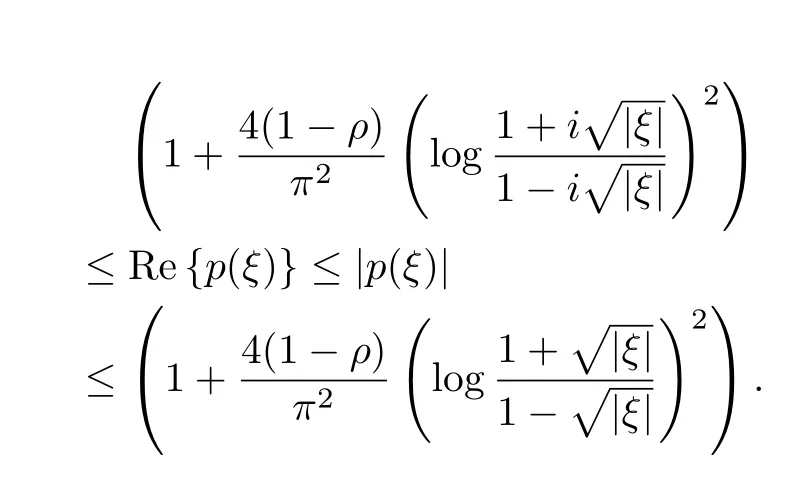
Let ξ=‖x‖，then

and

ProofBy Definition 2，we know that f is also a spirallike mapping of type β.For fixed x∈B｛0｝，let x（t）=f-1（exp（-e-iβt）f（x））,t∈［0,+∞）.By Lemma 1，‖x（t）‖is differentiable almost everywhere on［0,+∞）and

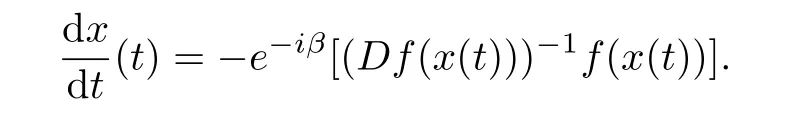
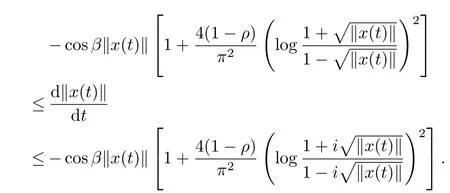
Since

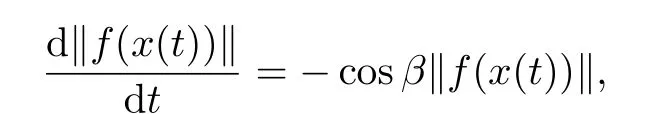
we have

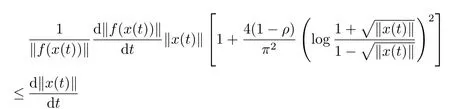
For γ∈（0,1），integrating on both sides of the above left-hand inequality with respect to t∈［0,γ］,we have

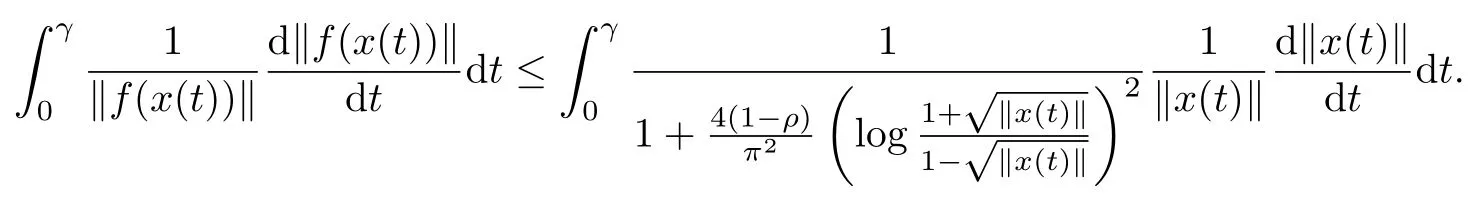
Thus it is

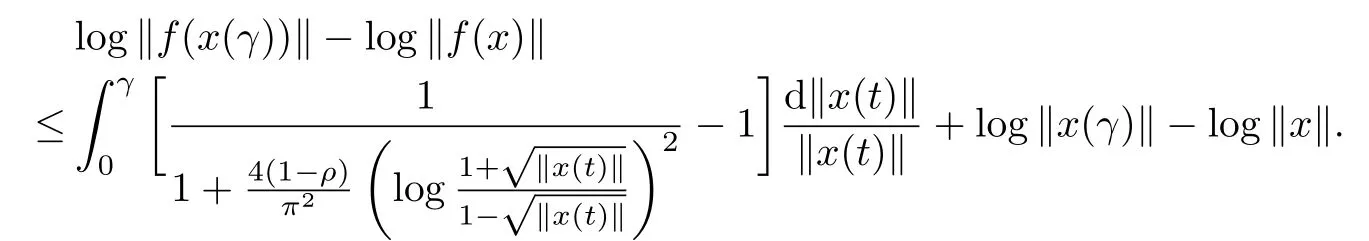
Hence，

Let γ→+∞，

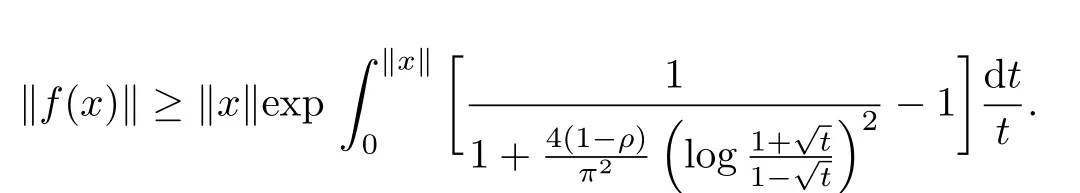
By the same reason as above，we can obtain

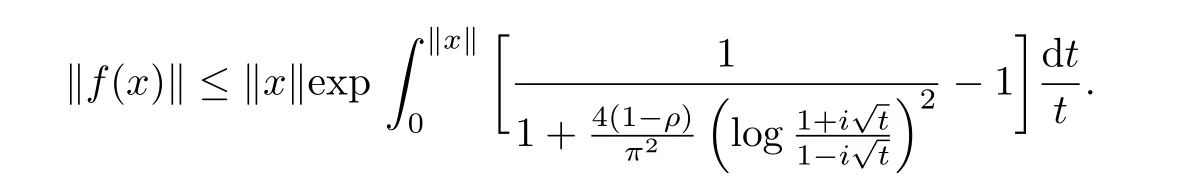
In particular，the result of Zhang and Feng［4］can be got when β=0.

CorollaryLet ρ∈［0,1），f：B→X be a normalized biholomorphic parabolic starlike mapping of order ρ.Then for all x∈B holds

§3.The Distortion Theorem for PS（β；ρ）along Unit Direction

In one complex variable，the classical distortion for normalized biholomorphic functions（see inequality（2.2））is well known.In several complex variables，however，there are many counterexamples to show that the distortion theorem fails if we do not restrict some subclasses of biholomorphic mappings.The first afirm ative result about the distortion theorem for detJf（z）was established by Barnard，FitzGerald and Gong［16］，when f is a normalized biholomorphic convex mappings in the unit ball B2of C2.And Liu and Zhang［17］extended it to the general case which were as follows.

Theorem［17］Let f：Bn-→Cnbe a normalized biholomorphic convex mapping，then

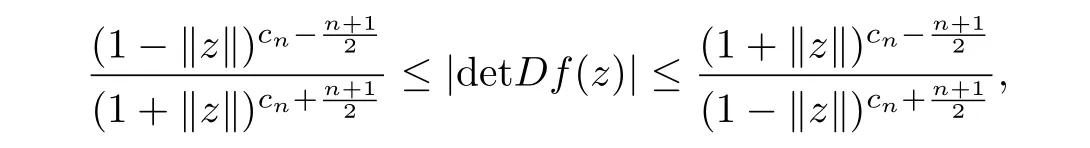
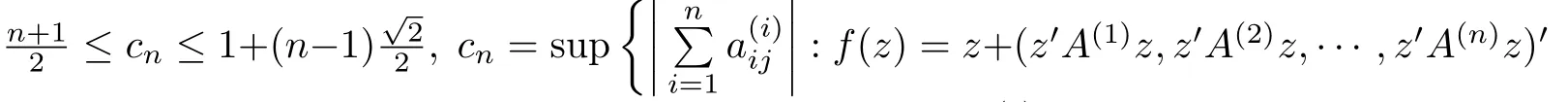
where +···is a normalized biholomorphic convex mappings on Bn，A（j）aresymmetric square matrix,In particular，

Henceforth，some distortion theorem for biholomorphic convex mappings came out，although there is little result for the distortion theorem of biholomorphic starlike mappings（see［18-24］）. In this part，as the application of Lemma 3 and the growth theorem for PS（β；ρ），we give the following distortion theorem for PS（β；ρ）along a unit direction.

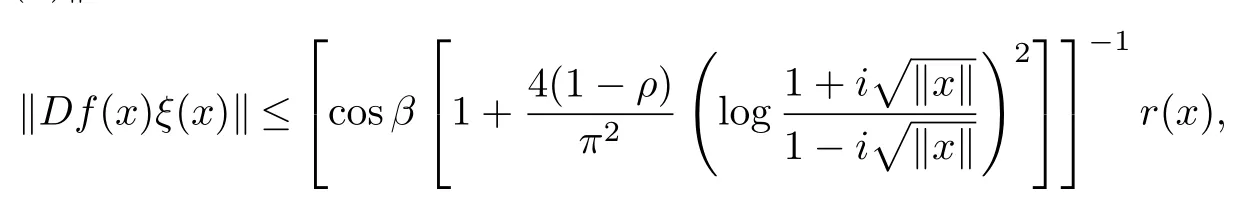
Since，by the inequality（2.4）of Lemma 3，

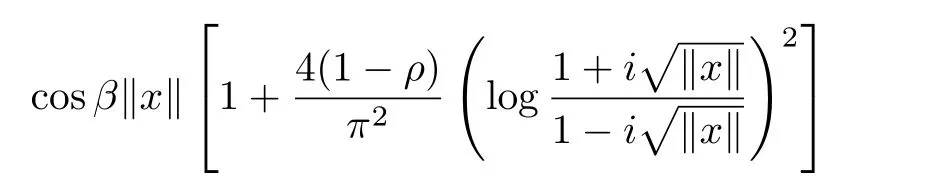
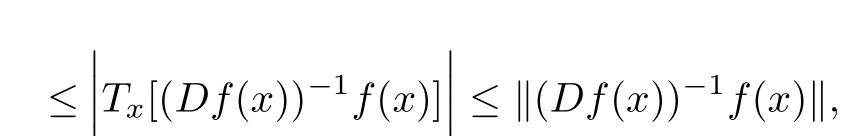
hence，by Theorem 1 in section 2 we have

CorollaryLet ρ∈［0,1），f：B→X be a normalized biholomorphic parabolic starlike mapping of order ρ.Then for all x∈B｛0｝，there exists a unit vectorsuch that

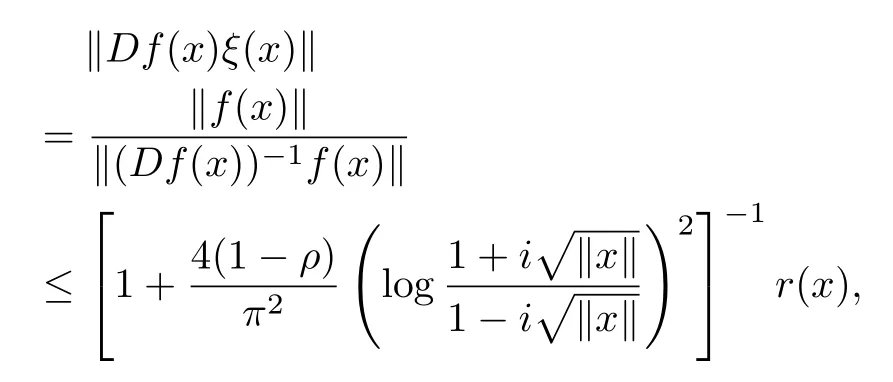
where r（x）=exp

［References］

［1］R∅NNING F.Uniformly convex functions and a corresponding class of starlike functions［J］.Proc Amer Math Soc，1993，118（1）：189-196.

［2］ALI R M.Starlikeness associated with parabolic regions［J］.Int J Math Math Sci，2005，4（2005）：561-570.

［3］HAMADA H，HONDA T，KOHR G.Parabolic starlike mappings in several complex variables［J］.Manuscripta mathematica，2007，123（3）：301-324.

［4］ZHANG Xiao-fei，FENG Shu-xia.Some estimations for parabolic starlike mappings of order ρ on the unit ball in Cn［J］.Chin Ann Math，2013，34A（2）：147-160.

［5］ZHANG Xiao-fei，FENG Shu-xia，CHEN Hui-yong.Parabolic starlike mappings in several complex variables［J］.Acta Math Sinica，2011，54A（3）：467-482.

［6］GRAHAM I，KOHR G.Geometric Function Theory in One and High Dimensions［M］.New York：Pure and Applied Mathematics，2003.

［7］DUREN P L.Univalent Function［M］.Berlin：SpringerVerlag，1983.

［8］CARTAN H.Sur la Possibilit´e D'´etendre Aux Fonctions de Plusieurs Variables Complexes la Th´eorie des Fonctions Univalentes，Lecons Sur Les Fonctions Univalentes ou Multivalentes［M］.Paris：Gauthier-Villars，1933.

［9］BARNARD R W，FITZGERALD C H，GONG Sheng.The growth andtheorems for starlike mappings in Cn［J］.Pacific J Math，1991，150（1）：13-22.

［10］LIU Tai-shun，REN Guang-bin.The growth theorem of convex mappings on bounded convex circular domains［J］.Sci Chin，1998，41A：123-130.

［11］LIU Tai-shun，REN Guang-bin.The growth theorem for starlike mappings on bounded starlike circular domains［J］.Chin Ann Math，1998，19B（4）：401-408.

［12］HAMADA H，KOHR G.Growth and distortion results for convex mappings in infinite dimensional spaces［J］. Complex Variables，2002，47：291-301.

［13］HAMADA H，HONDA T，KOHR G.Growth theorems and coefficient bounds for univalent holomorphic mappings which have parametric representation［J］.J Math Anal Appl，2006，317：302-319.

［14］LIU Hao，LI Xiao-shen.The growth theorem for strongly starlike mappings of order α on bounded starlike circular domains［J］.Chin Quart J of Math，2000，15（3）：28-33.

［15］FENG Shu-xia，LIU Tai-shun，REN Guang-bin.The growth and covering theorems for several mappings on the unit ball in complex Banach space［J］.Chin Ann Math，2007，28A：215-230.

［16］BARNARD R W，FITZGERALD C H，GONG Sheng.A distortion theorem for biholomorphic mappings in C2［J］.Tran Amer Math Soc，1994，344：902-924.

［17］LIU Tai-shun，ZHANG Wen-jun.A distortion theorem for biholomorphic convex mappings in Cn［J］.Chin Jour Contemporary Math，1999，20（3）：421-430.

［18］GONG Sheng，WANG Shi-kun，YU Qi-huang.Biholomorphic convex mappings of ball in C2［J］.Pacific J Math，1993，161（2）：287-306.

［19］GONG Sheng，LIU Tai-shun.Distortion theorems for biholomorphic convex mappings on bounded convex circular domains［J］.Chin Ann Math，1999，20B（3）：297-304.

［20］LIU Tai-shun，ZHANG Wen-jun.A distortion theorem of biholomorphic convex mappings in a Banach space［J］.Acta Math Sinica，2003，46A（6）：1041-1046.

［21］ZHANG Xiao-fei，LIU Tai-shun，LU Jin.The growth，covering and distortion theorems for a subclass of convex mappings［J］.Complex Variables and Elliptic Equations，2015，60（6）：787-800.

［22］LIU Tai-Shun，WANG Jian-fei，LU Jin.Distortion theorems of starlike mappings along a unit direction in Cn［J］.Taiwanese J Math，2011，15（6）：2601-2608.

［23］LU Jin，LIU Tai-Shun，WANG Jian-fei.The distortion theorems for k-fold symmetric quasi-convex mappings along a unit direction in Cn［J］.Chin Quart J of Math，2012，27（4）：475-479.

［24］LU Jin，LIU Tai-Shun，WANG Jian-fei.Distortion theorems for subclasses of starlike mappings along a unit direction in Cn［J］.Acta Math Scienti，2012，32B（4）：1675-1680.

O174.56Document code：A

date：2015-09-03

Supported by the Doctoral Foundation of Pingdingshan University（PXY-BSQD-20150 05）；Supported by the Natural Science Foundation of Zhejiang Province（Y14A010047）；Supported by the the Key Scientific Research Projects in Universities of Henan Province（16B110010）；Supported by the Foster Foundation of Pingdingshan University（PXY-PYJJ2016007）

Biography：ZHANG Xiao-fei（1982-），male，native of Xuchang，Henan，a lecturer of Pingdingshan University，Ph.D.，engages in function theory of several complex variables.