Unbounded Motions in Asymmetric Oscillators Depending on Derivatives

WANG Li-xia，MA Shi-wang，WANG Xiao-ming

（1.School of Science，Tianjin Chengjian University，Tianjin 300384，China；2.School of Mathematical Sciences and LPMC，Nankai University，Tianjin 300071，China；3.School of Mathematics and Computer Science，Shangrao Normal University，Shangrao 334001，China）



Unbounded Motions in Asymmetric Oscillators Depending on Derivatives

WANG Li-xia1，MA Shi-wang2，WANG Xiao-ming3

（1.School of Science，Tianjin Chengjian University，Tianjin 300384，China；2.School of Mathematical Sciences and LPMC，Nankai University，Tianjin 300071，China；3.School of Mathematics and Computer Science，Shangrao Normal University，Shangrao 334001，China）

In this paper，we consider the unboundedness of solutions for the asymmetric equation

unboundedness；resonance；nonresonance

§1.Introduction

A simple second-order differential equation with asymmetric nonlinearities

was firstly studied by Dancer［45］and Fuˇcik［6］in their investigations of boundary value problems associated to equations with“jumping nonlinearities”.The interest for such equations has beenmotivated in particular by models of suspension bridges.The boundedness of all the solutions，the existence of periodic or unbounded solutions for（1.1）have been widely studied in the literature.It was well known that under the resonance condition

for some relatively prime integers p and q，the existence of bounded or unbounded solutions for the asymmetric oscillator（1.1）essentially depends on the property of the function Φp（θ）defined by

In 2002，based on an abstract result contained in［2］，Dambrosio［3］obtained the existence of unbounded solutions for the equation where a and b satisfy the resonance condition（1.2）and g（x）is bounded and admits generalized limits at infinity.

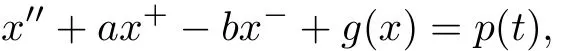
In 2003，Wang［14］studied the existence of unbounded solutions of the following equation

where a,b are some positive constants satisfying the nonresonance condition

He showed that the corresponding Poincar´e mapping in generalized coordinates can be written in the following form

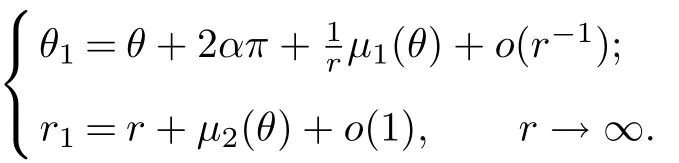
Then every solution x（t）with initial value satisfying1,goes to infinity in the future or in the past if

Based on Wang's results，Li and Zhang［8］showed the coexistence of unbounded solutions and periodic solutions for the asymmetric oscillator

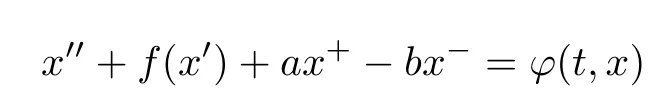
under the nonresonant condition（1.4）and the limits

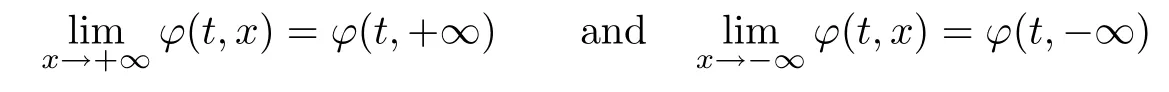
exist uniformly in t.

For more results on the unboundedness of solutions for asymmetric oscillators，we refer the readers to［2，6-7，10-13］and references therein.

Recently，Wang［1516］investigated the existence of periodic solutions of equations with asymmetric nonlinearities depending on the derivatives

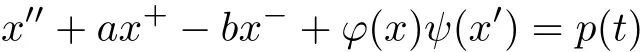
and

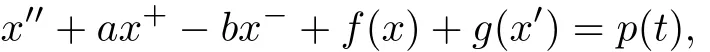
respectively.The study of periodic solutions and Dirichlet problems for such an equation has attracted the attention of researchers recently.In 1952，Reuter and Ascari［1］studied positive direction boundedness of the equation

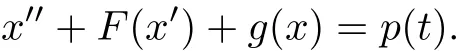
However，the unboundedness problems of solutions of such equations with asymmetric nonlinearities depending on the derivatives in R has seen relatively little research.In this paper，we will deal with the unboudedness of solutions for a more general equation

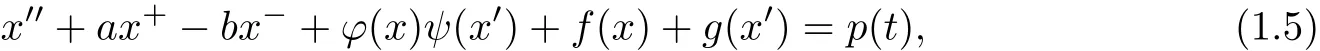
where x+=max｛x,0｝,x-=max｛-x,0｝，a and b are two different positive constants，f（x）is bounded and admits generalized limits at infinity，ϕ（x）,ψ（x）,g（x）and p（t）are continuous functions，and p（t）is a 2π-periodic function.Under two classes of conditions：the resonance caseand the nonresonance case，some conclusions will be obtained with respect to（1.5）.

To state our main results，we firstly give some notations.Let

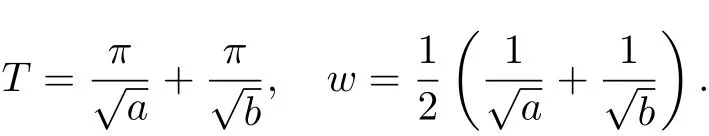
Let（C（t）,S（t））be the unique solution of the autonomous system

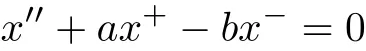
satisfying the initial condition（C（0）,S（0））=（1,0）.Then C（t）and S（t）are T-periodic and C（t）∈C2（R）,S（t）∈C1（R）.Moreover C（t）is even and can be given by

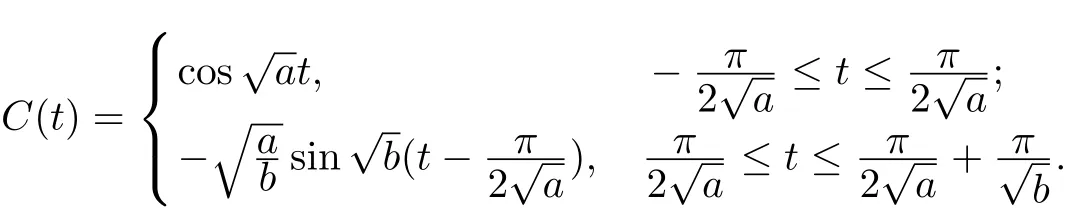
Remark 1.1The functions C（t）and S（t）are introduced in［2］，however，there is a small mistake in the presentation，for

Let C]（t）and S]（t）be the average functions of C（t）and S（t），respectively.

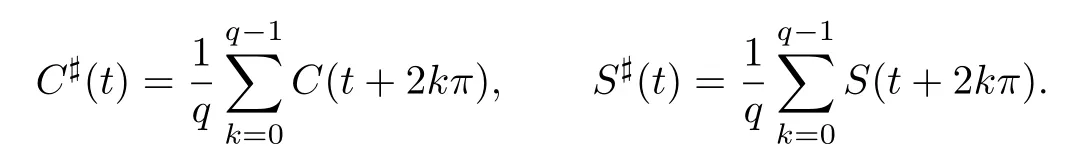
Let Φp：C（R/2πZ）7→C1（R/2πq-1Z）be the linear operator，defined by（1.3）for every p∈C（R/2πZ）.It is easy to check that Φpis a 2π/q-periodic function whose derivative is given by

Remark 1.2Liu［9］has proved that the function Φpin（1.3）is the same as the definition given by Ortega［2］，that is

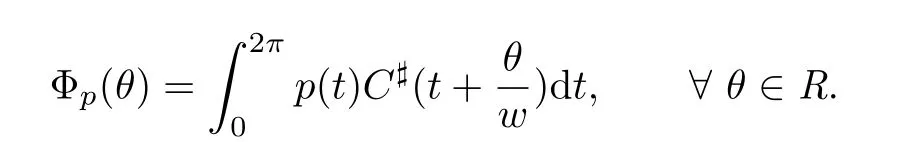
In this paper，we always assume that

（H2）f is locally Lipschitz bounded function and admits generalized limits at infinity，i.e.，

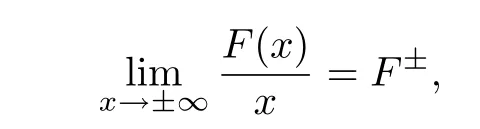
where F（x）=

For the sake of convenience，in later discussions we will set

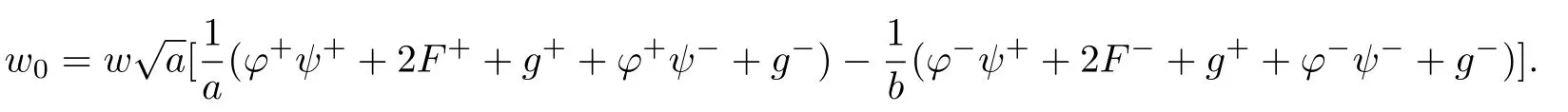
For the resonance case，we have the following results.

Theorem 1Assume that（H1），（H2）and（1.2）hold，and suppose that there exists θ0such that Φp（θ0）=w0；moreover，assume that if there is θ∈R such that Φp（θ）=w0，then

Then，there exists R0＞0 such that every solution x（t）of（1.5）with，for some t0∈R，satisfies

Theorem 2Assume that（H1），（H2）and（1.2）hold with q=1，and that Φp（θ）＞w0for every θ∈R.Then，there exists at least one 2π-periodic solution of（1.5）.

For the nonresonance case

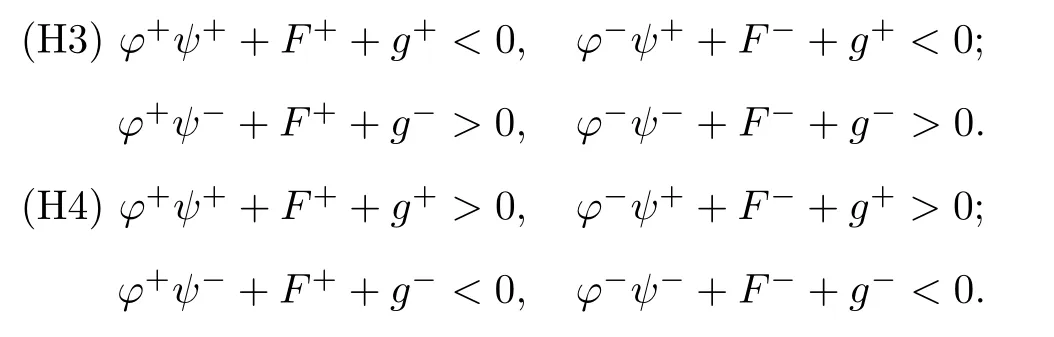
Theorem 3Assume that（H1），（H2），（H3）and（1.4）hold.Then there exists R0＞0 such that every solution x（t）of（1.5）with

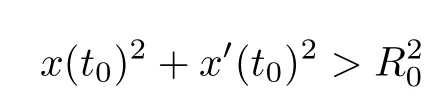
with t0∈R goes to infinity in the future.

Theorem 4Assume that（H1），（H2），（H4）and（1.4）hold.Then there exists R0＞0 such that every solution x（t）of（1.5）with

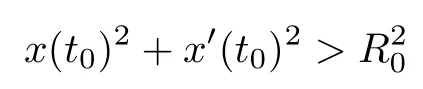
with t0∈R goes to infinity in the past.

The rest of the paper is organized as follows.In Section 2 we give some transformations and estimates.We will prove main results in Section 3 and Section 4.

§2.Canonical Transformations and Some Estimates

In this section，we change（1.5）into a planar system by means of a series of transformations and give some approximate expression for the solutions，then give the Poincar´e map of（1.5）. To this end，the following result is needed.

Lemma 2.1［3］Assume that g：R→R is a locally Lipschitz function satisfying

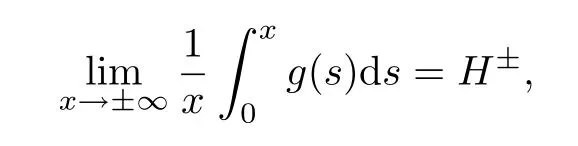
then there exists a decomposition g=ψ+h，where ψ（±∞）=0 in a generalized sense and

According to Lemma 2.1，we split the function f in（1.5）as f=f1+f2.We denote by F1and F2the primitives of f1and f2，respectively，such that F1（0）=0=F2（0），

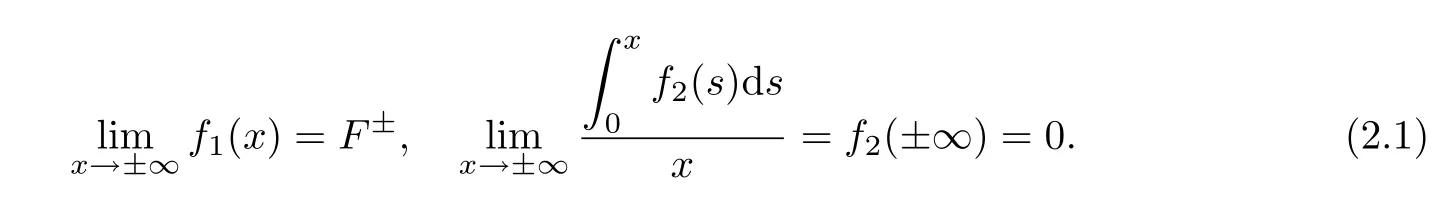
Now we consider the equivalent system of（1.5），

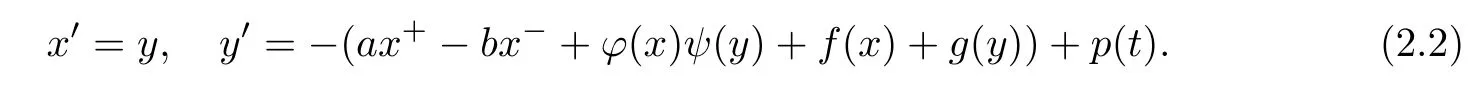
Define the mapping Φ：（θ,I）∈S1×（0,+∞）→（x,y）∈R2｛0｝as follows

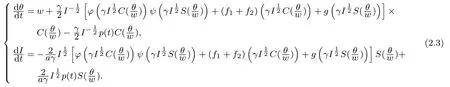
Denote by（θ（t；θ0,I0）,I（t；θ0,I0））the solution of（2.3）satisfying the initial value θ（0）=θ0,I（0）=I0.Assume that f1and f2are locally Lipschitz and bounded，ϕ,ψ and g are bounded，according to Lemma 2.5［3］，then for large values of I0，this solution is defined for all t∈［0,2π］. So we can define the Poincar´e mapping

From the second equality of（2.3），we get that

By Lemma 2.5［3］，it follows from（2.4）that

Furthermore，we have that

From（2.5）and the first equality of（2.3），we have that）.Consequently，

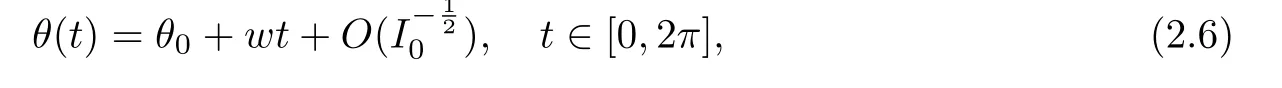
which，together with（2.5），yields

We integrate（2.7）from 0 to 2π

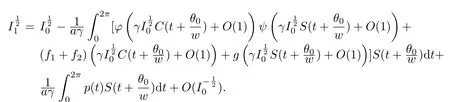
Similarly，substituting（2.6）in the first equality of（2.3），we obtain that for t∈［0,2π］，

By integrating（2.8）on［0,2π］，we have

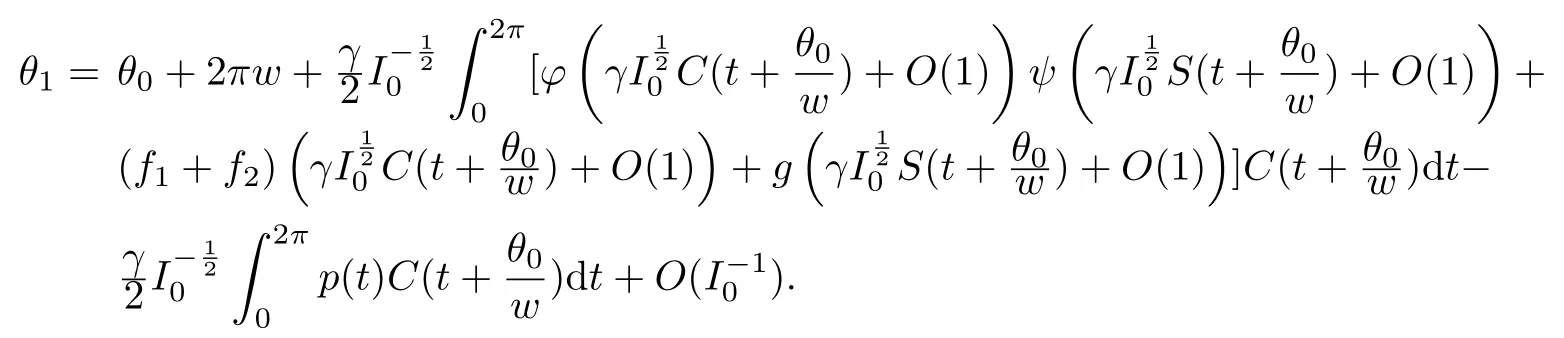
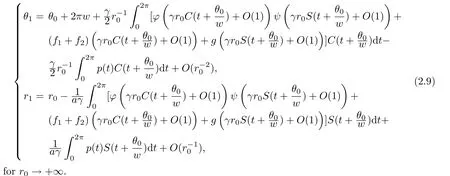
We define

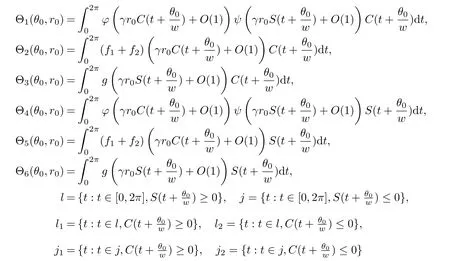
and

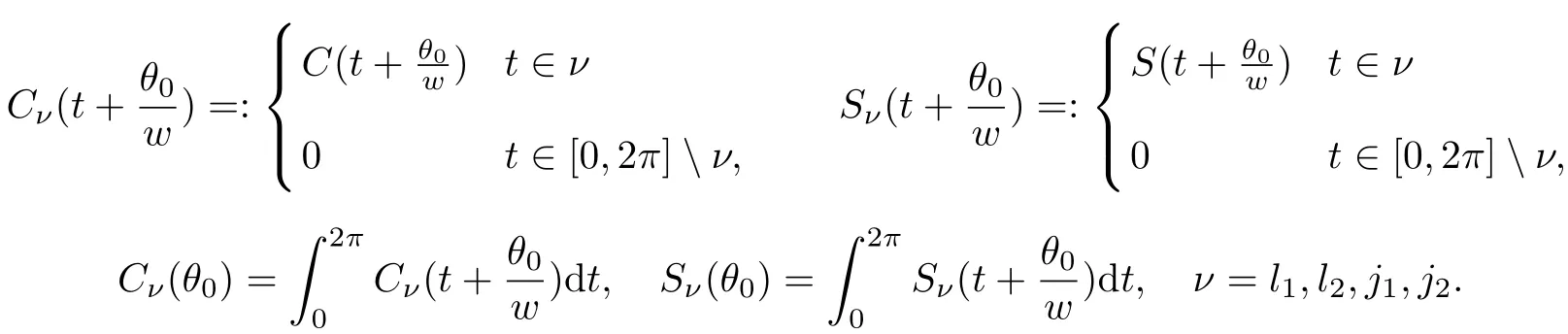
Lemma 2.2［3］Assume that

Then，for every continuous function v such that v（t）=O（1）as r0→+∞，uniformly in t∈［0,2π］，we have

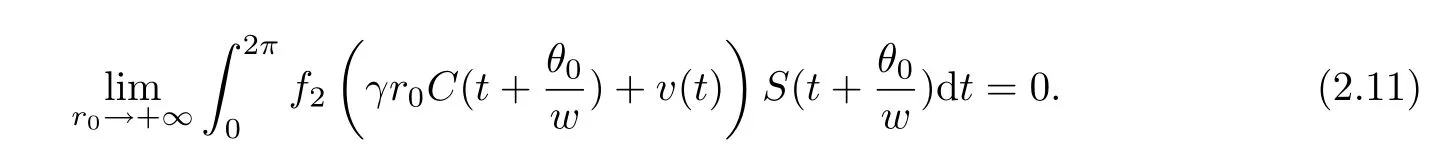
Similarly，we have

By Lemma 2.9［3］，we have

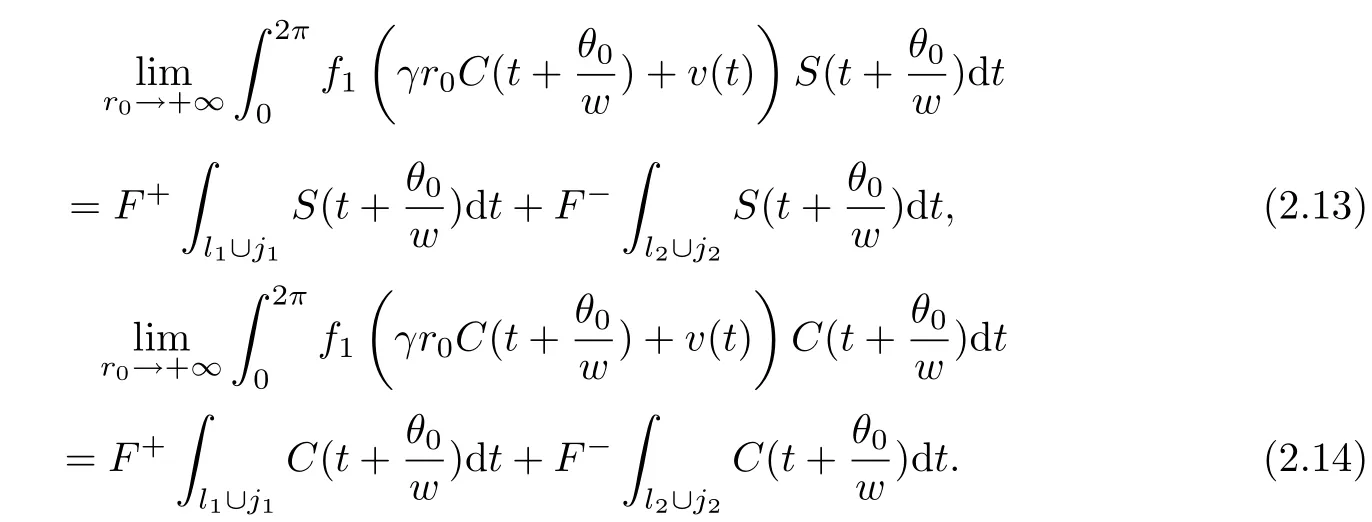
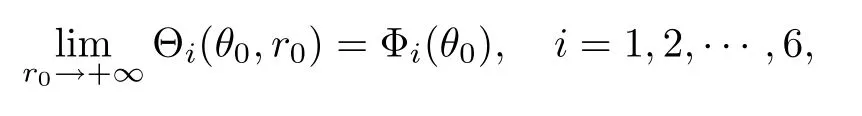
where

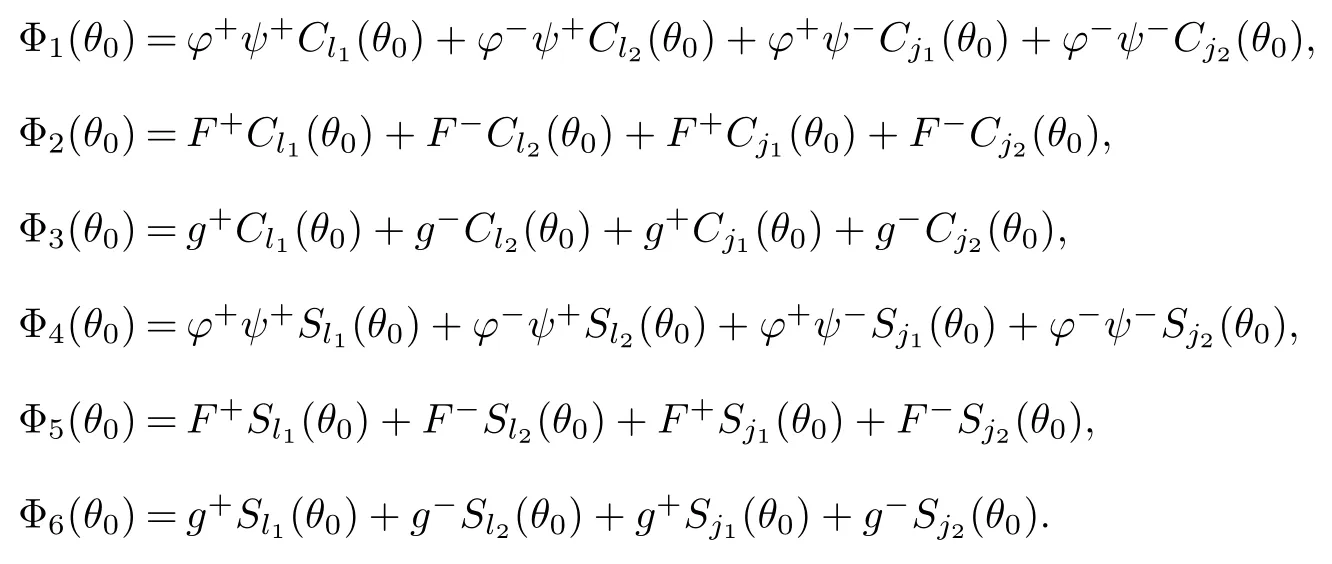
Lemma 2.3Assume that（H1）and（H2）hold.Then

ProofWe only check that the second limit of Lemma 2.3.By the boundedness of f1,f2and C，we can apply the Lebesgue dominate convergence theorem（for r0→+∞）to both the integrals on right-hand side of the following equality，using Lemma 2.2 and（2.14），we have the following

§3.Proofs of Theorem 1 and Theorem 2

In this section，we will prove Theorem 1.Now we assume that all the conditions of Theorem 1 hold.Theorem 1 will be a consequence of the application of an abstract result，due to Alonso and Ortega［2］，concerning the dynamics of a class of planar mappings.We need some preliminaries.

Let σ＞0，we define Eσ=｛（θ,r）∈R×（0,+∞）：r≥σ｝.Let P1：Eσ7→R2be a one-to-one and continuous mapping of the form

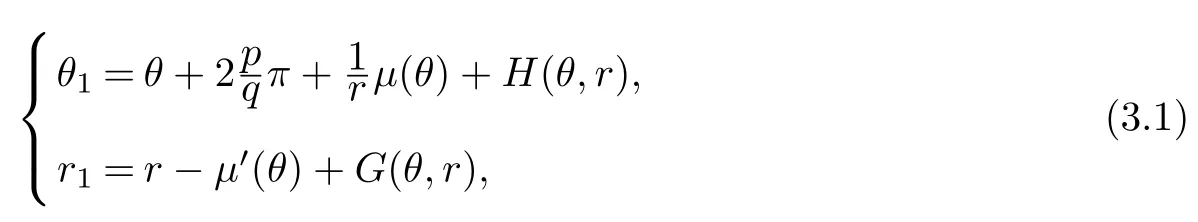
whereµ∈C1（R）is 2π-periodic and H,G are continuous functions 2π-periodic in θ satisfying the condition

uniformly with respect to θ∈R as r→+∞.

For any（θ0,r0）∈Eσ，denote by｛（θn,rn）｝the orbit of the mapping P1through the point（θ0,r0）.That is to say（θn+1,rn+1）=P1（θn,rn）.By introducing the function

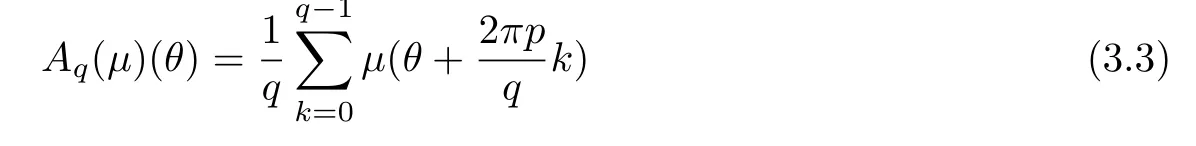
（A1（µ）=µ），in［2］the authors proved the following.

Lemma 3.1［2］Assume thatµ∈C1（R）is 2π-periodic and that（3.2）holds.Moreover，we suppose that there exists ω∈R such that

and that

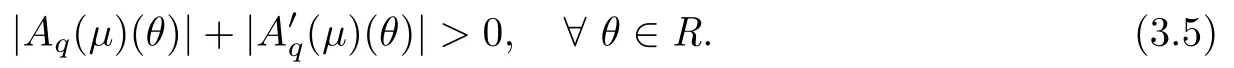
Then，there exists R≥σ such that for every r0≥R the solution｛（θn,rn）｝of（3.1）is defined either in the future or in the past and satisfies

Now，in view of the application of Lemma 3.1，let us set

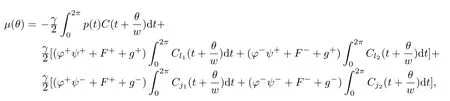
for every θ∈［0,2π］.From（2.9）and the definition ofµ，we can deduce that the final expression for the asymptotic expansion of（1.5）is

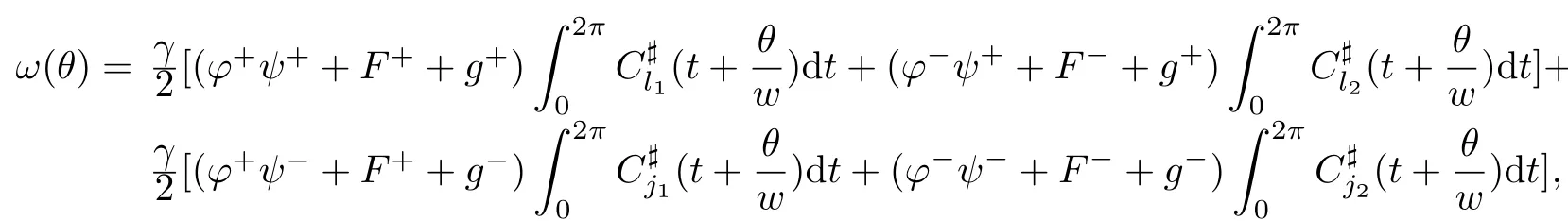
for every θ∈［0,2π］.Since，as already observed，C]v（v=l1,l2,j1,j2）are 2πq/p periodic functions.By Lemma 2.10［3］and a computation of integral of the function C and S，we deduce that ω（θ）is constant

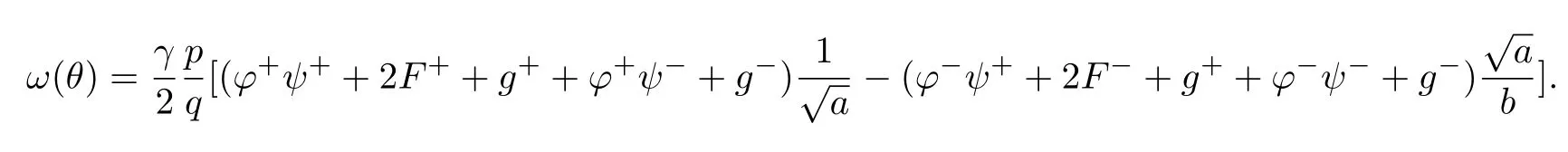
Proof of Theorem 2The proof of Theorem 2 is similar to the proof of Theorem 2.11［3］，we omit it here.

§4.Proofs of Theorem 3 and Theorem 4

The proofs of our main theorems 3 and 4 are based on an abstract result due to Wang［14］，which describes the dynamics of a class of planar mappings when suitable conditions on the behavior of the map at infinity are assumed.

Assume that σ is defined in Section 3.Let P：Eσ→R2is a one-to-one and continuous mapping of the form

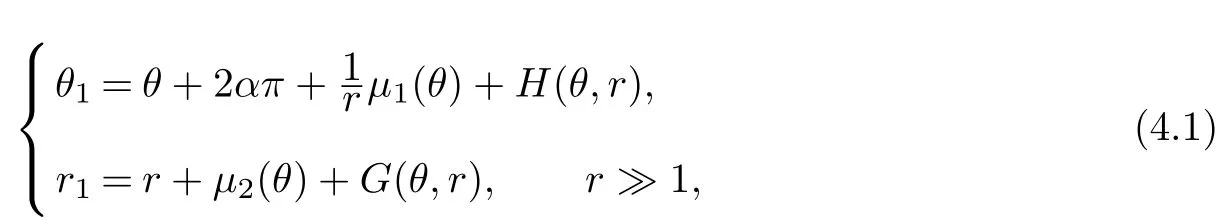
where

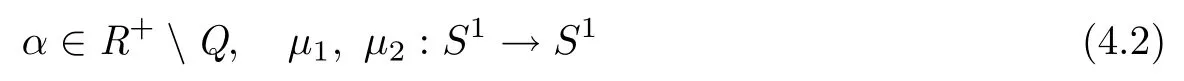
are Lipschitz continuous，S1=R/2πZ.H and G are continuous functions，which are 2π-periodic in θ and satisfy

For any（θ0,r0）∈Eσ，denote by｛（θn,rn）｝the orbit of the mapping P through the point（θ0,r0）.That is to say（θn+1,rn+1）=P（θn,rn）.

The following abstract results taken from［14］will be applied to prove our main Theorem 3 and Theorem 4.

Lemma 4.1Assume that the conditions（4.2），（4.3）hold and.Then there exists R0＞σ such that if r0＞R0，the orbit｛（θn,rn）｝satisfies

Lemma 4.2Assume that the conditions（4.2），（4.3）hold and.Then there exists R0＞σ such that if r0＞R0，the orbit｛（θn,rn）｝satisfies

We only give the proof of Theorem 3.The proof of Theorem 4 is similar and thus is omitted. Consider the Poincar´e mapping P：（θ0,r0）→（θ1,r1）.From Lemma 2.1，Lemma 2.2，Lemma 2.3，we know that P can be expressed in the form of

where H,G are continuous functions satisfying

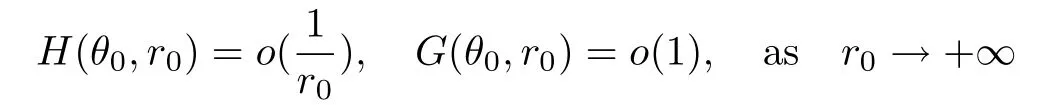
and

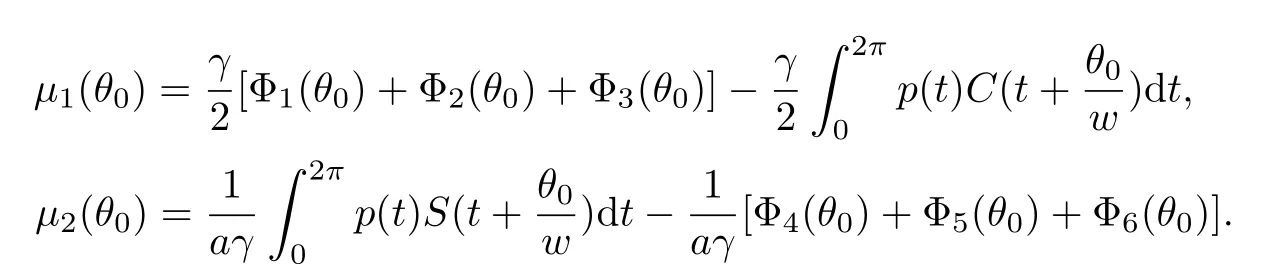
In view of（H3），we have thatBy computing，we get that

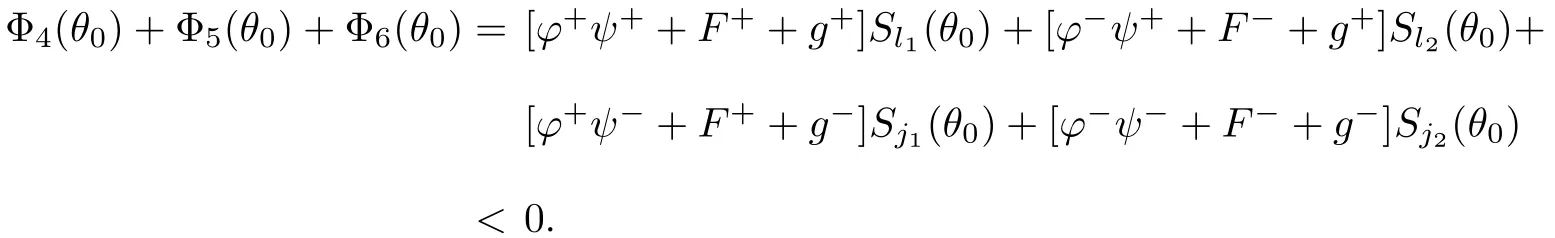
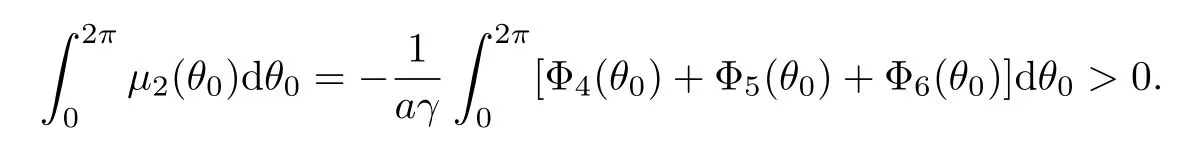
Applying Lemma 4.1 to Poincar´e mapping P，we obtain the proof of the unboundedness of solutions of（1.5）.

［1］ASCARI A.Studio asintotico di un'equazione relative alla dinamica del punto［J］.Rend Istit Lomb Sci Lett，1952，16：278-288.

［2］ALONSO J M，ORTEGA G.Roots of unity and unbounded motions of an asymmetric oscillator［J］.J of Differential Equations，1998，143：201-220.

［3］DAMBROSIO W.A note on the existence of unbounded solutions to a perturbed asymmetric oscillator［J］. Nonlinear Anal，2002，50：333-346.

［4］DANCER N.Boundary-value problems for weakly nonlinear ordinary differential equations［J］.Bull Austral Math Soc，1976，15：321-328.

［5］DANCER N.On the Dirichlet problem for weakly nonlinear elliptic partial equations［J］.Proc Roy Soc Edinburgh，1977，A76：283-300.

［6］FUCIK S.Solvability of Nonlinear Equations and Boundary Value Problem［M］.Dordrecht，Boston，London：D RElDEL Publishing Company，1980.

［7］KUNZE M，K¨UPPER T，LIU Bin.Boundedness and unboundedness solutions of reversible oscillators at resonance［J］.Nonlinearity，2001，14：1105-1122.

［8］LI Xiong，ZHANG Zi-heng.Unbounded solutions and periodic solutions for second order differential equations with asymmetric nonlinearity［J］.Proc Amer Math Soc，2007，135（9）：2769-2777.

［9］LIU Bin.Boundedness in asymmetric oscillations［J］.J Math Anal Appl，1999，231：355-373.

［10］ORTEGA R.Asymmetric oscillators and twist mappings［J］.J London Math Soc，1996，53（2）：325-342.

［11］QIAN Ding-bian.Resonance phenomena for asymmetric weakly nonlinear oscillator［J］.Science in China，2002，45（2）：214-222.

［12］SI Jian-guo.Invariant tori and unboundedness for second order differential equations with asymmetric nonlinearities depending on the derivatives［J］.Nonlinear Anal，2007，67：3098-3115.

［13］WANG Li-xia，MA Shi-wang.Unboundedness of solutions for perturbed asymmetric oscillators［J］.Dis Con Dyn Syst B，2011，16（1）：409-421.

［14］WANG Zai-hong.Irrational rotation numbers and unboundedness of solutions of the second order differential equations with asymmetric nonlinearities［J］.Proc Amer Math Soc，2003，131（2）：523-531.

［15］WANG Zai-hong.Periodic solutions of the second order differential equations with asymmetric nonlinearities depending on the derivatives［J］.Dis Con Dyn Syst 2003，9（3）：751-770.

［16］WANG Zai-hong.The existence of periodic solutions of the second order differential equations with jumping nonlinearities depending on the derivatives［J］.Chines Ann Math（in Chinese），2003，24：47-58.

O175.1Document code：A

1002—0462（2016）02—0189—12 Chin.Quart.J.of Math. 2016，31（2）：189—200

Received date：2014-10-15

Foundation item：Supported by the Tianyuan Special Foundation（11526148）；Supported by the National Natural Science Foundation of China（11571187，11461056）

Biographies：WANG Li-xia（1982-），female，native of Shijiazhuang，Hebei，a lecturer of Tianjin Chengjian University，Ph.D.，engages in dynamical system and differential equations；MA Shi-wang（1968-），male，native of Eerduosi，Neimenggu，a professor of Nankai University，Ph.D.，engages in dynamical system and differential equations；WANG Xiao-ming（corresponding author）（1978-），male，native of Yushan，Jiangxi，an associate professor of Shangrao Normal University，engages in dynamical system and differential equations.

where x+=max｛x，0｝，x-=max｛-x，0｝，a and b are two different positive constants，f（x）is locally Lipschitz continuous and bounded，ϕ（x），ψ（x），g（x）and p（t）are continuous functions，p（t）is a 2π-periodic function.We discuss the existence of unbounded solutions under two classes of conditions：the resonance caseand the nonresonance case

2000 MR Subject Classification：34C25，37B30，37J45