Some Inequalities for the General Radial Bodies
2016-09-15ZHANGPingWANGWeidong
ZHANG Ping,WANG Wei-dong
(Department of Mathematics,China Three Gorges University,Yichang 443002,China)
Some Inequalities for the General Radial Bodies
ZHANG Ping,WANG Wei-dong
(Department of Mathematics,China Three Gorges University,Yichang 443002,China)
Lutwak showed the radial bodies combining with the radial Minkowski linear combinations of star bodies.In this paper,the general radial bodies are introduced and its some properties and inequalities are established.
star body;dual mixed volume;general radial body
2000 MR Subject Classification:52A40,52A20
Article ID:1002—0462(2016)02—0171—07
Chin.Quart.J.of Math.
2016,31(2):171—177
§1.Introduction
Let Sn-1denote the unite sphere in n-dimension Euclidean space Rn.If K is a compact star shaped(with respect to the origin)in Rn,then its radial function ρK=ρ(K,·):Rn{0}-→[0,∞),is defined by(see[1])

If ρKis positive and continuous,K will be called a star body(about the origin).Letdenote the set of star bodies(about the origin)in Rn.For the set of origin-symmetric star bodies in Rn,we write
The notion of radial Minkowski linear combination is given by Lutwak(see[2]).For K,L∈Sno,λ,µ≥0(not both zero),the radial Minkowski linear combination,λ◦Ke+µ◦L,of K and L is defined by
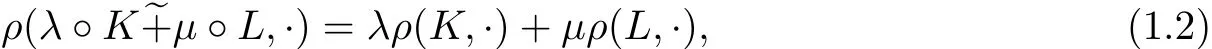

Associated with(1.2)~(1.3),Lutwak gave the following inequality(see[2]).
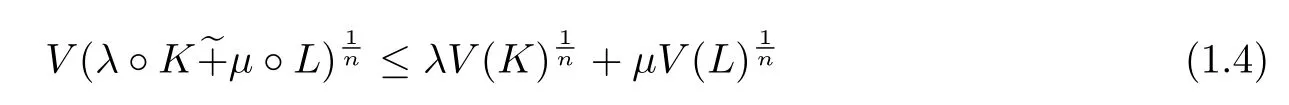
with equality if and only if K and L are dilates.
Note that inequality(1.4)is a dual form of the Brunn-Minkowski inequality.Recently,an isolate form of the Brunn-Minkowski inequality was obtained(see[3]).
From(1.3)and(1.4),Lutwak gave an inequality for radial bodies as follows(see[2]).

with equality if and only if K is origin-symmetric.
In this paper,we extend the notion of radial bodies to one parameter family of radial bodies which may be called general radial bodies.
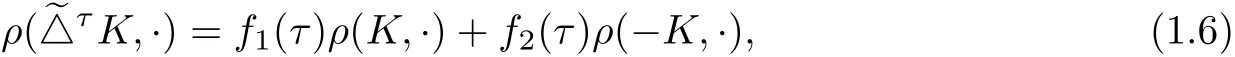
i.e.,

where

Obviously,we have
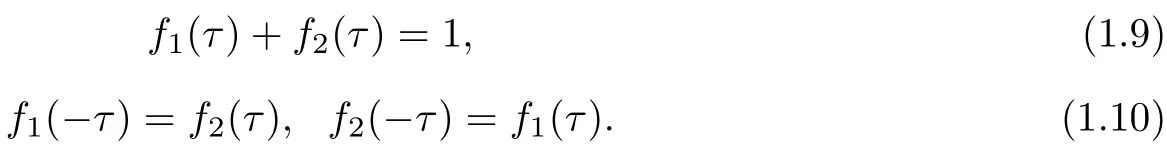
From(1.7)and(1.8),we see that if τ=0,then
The main goal of this paper is to give the extremum value for the general radial bodies.

if K is not origin-symmetric,then equality holds in the left inequality of(1.11)if and only if τ=0 and equality holds in the right inequality of(1.11)if and only if τ=±1.

then

equalities hold in(1.12)and(1.13)if and only if K=L in

equality holds in(1.14)if and only if
§2.Preliminaries
From(1.1),we have that for all u∈Sn-1,

and
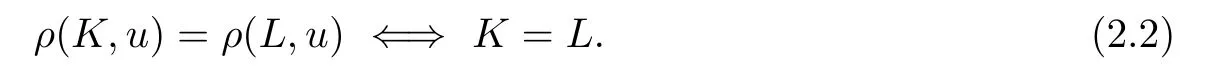
In addition,let φ∈GL(n),then it follows from the definition of ρKthat(see[1])
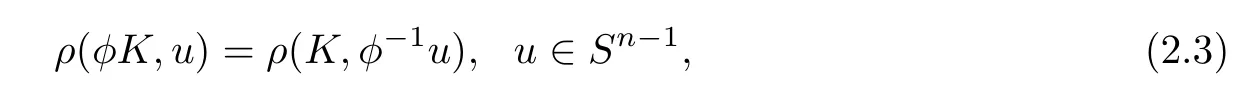
where GL(n)denotes the group of general(nonsingular)linear transformations and φ-1denotes the inverse of φ.
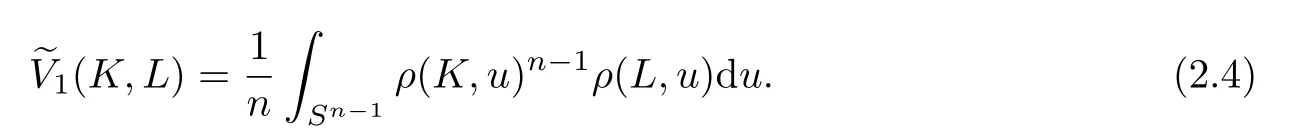
Clearly,for K,
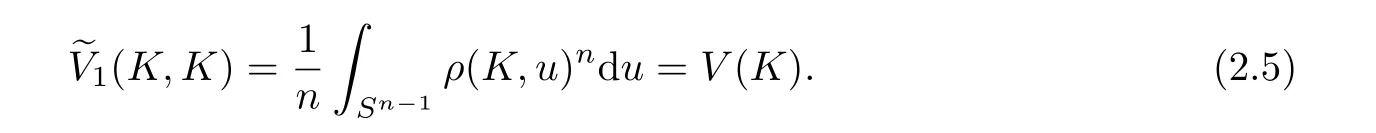
Associated with(1.2),an immediate consequence of(2.4)is that for any Q
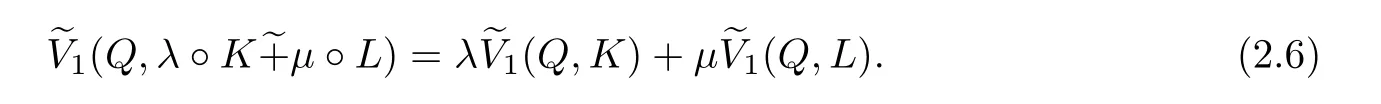
The dual Minkowski inequality can be stated that(see[4]).

From the dual Minkowski inequalities(2.7),it follows that
§3.Properties of General Radial Bodies
In this section,we discuss basic properties for the general radial bodies.

ProofFrom(2.3)and(1.6),then for any u∈Sn-1,
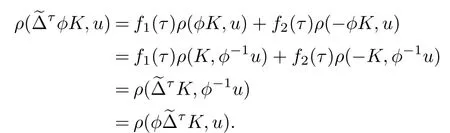
Thus by(2.2)we obtain
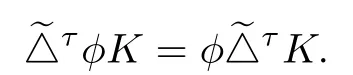
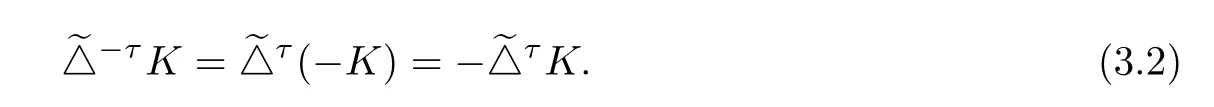
ProofFrom(1.6)and(1.10),it follows that for any u∈Sn-1,
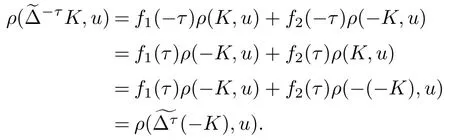
By(2.2),this gives

Further,from(2.1),we see that for any u∈Sn-1,
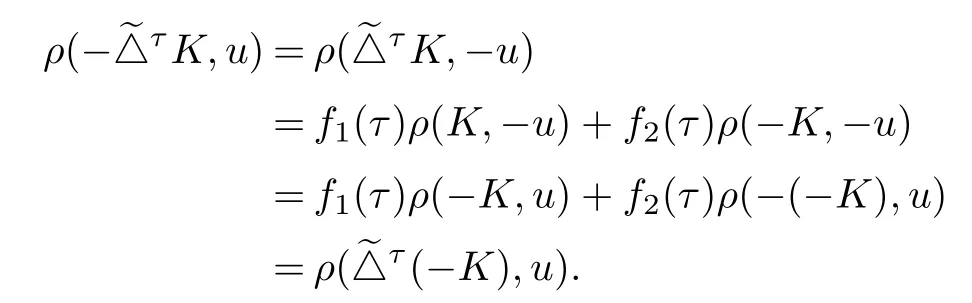
Hence,by(2.2)we have

From(3.3)and(3.4),we get(3.2).
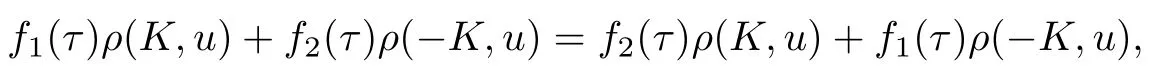
i.e.,
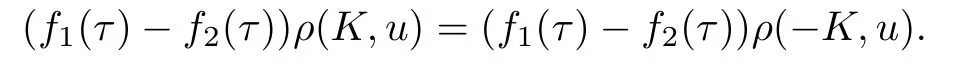
But f1(τ)-f2(τ)/=0 when τ/=0,this means that for any u∈Sn-1,ρ(K,u)=ρ(-K,u),i.e.,K=-K,so K is an origin-symmetric star body.
Conversely,if K is an origin-symmetric star body,i.e.,K=-K,combining with(3.2),we have
This together with(2.2),then

§4.Proofs of Main Results
In this section,we complete the proofs of theorems 1.1~1.3.
Proof of Theorem 1.1According to(1.4),for τ∈[-1,1],we have
From this,we get the right inequality of(1.11).
Obviously,if K is not origin-symmetric star body,then equality holds in the right inequality of(1.11)if and only if τ=±1.Therefore,if τ/=±1,then equality holds in the right inequality of(1.11)if and only K is an origin-symmetric star body.
Next,from(1.6),(1.9)and(1.10),then for any u∈Sn-1,
Therefore,
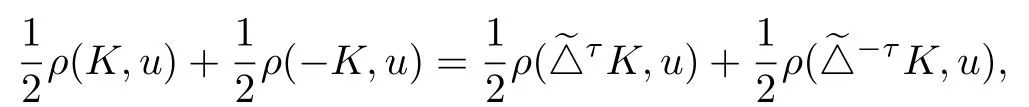
i.e.,
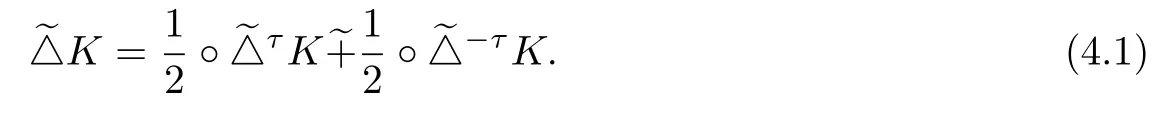
Together with(1.4)and(4.1),then

This gives the left inequality of(1.11).
From the equality condition of(1.4),we know that equality holds in the left inequality of(1.11)if and only ifandare dilates.So letand notice that),we get c=1,i.e.,According to Corollary 3.1,we see that if K is not origin-symmetric star body,then equality holds in the left inequality of(1.11)if and only if τ=0.
Proof of Theorem 1.2From(1.7)and(2.6),then
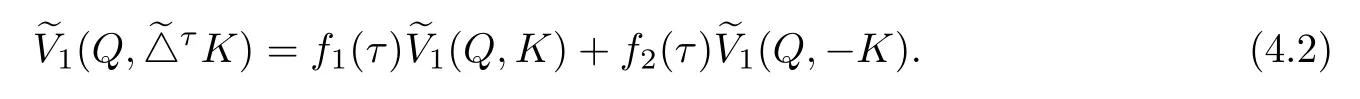
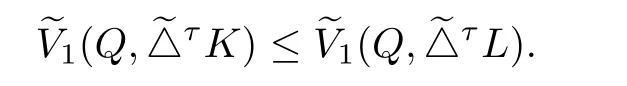
This and(4.2)yields
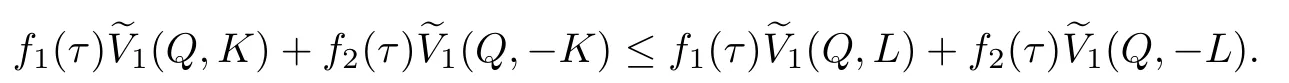

This together with inequalities(2.7)and(1.9),above inequality can be rewritten that
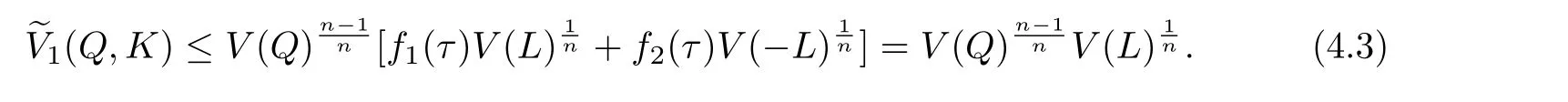
Let Q=K in(4.3)and use(2.5),then(1.13)can be obtained.
According to the equality condition of(2.7),we see that equality holds in(1.13)if and only if K and L are dilates in,this means that equality holds in(1.13)if and only if K=L in.But fromand Corollary 3.2,we know that equality holds in(1.12)if and only if K=L in Sns.Therefore,equalities hold in(1.12)and(1.13)if and only if K=L in Sns.
Proof of Theorem 1.3Since K⊆L,thus-K⊆-L.So from(2.4),for any Q∈Sno,
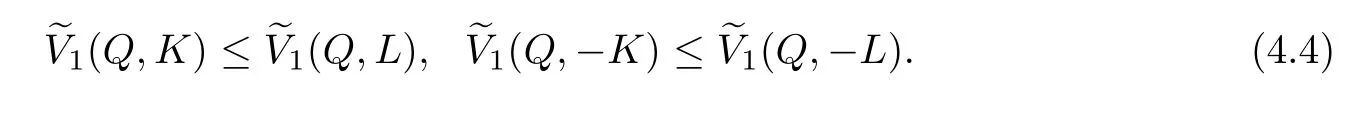
According to Theorem 2.B,we see that equality holds in(4.4)if and only if K=L.
Notice that f1(τ),f2(τ)≥0,then by(4.4)we get
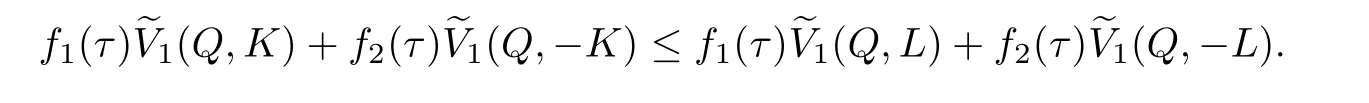
This combing with(4.2),we have
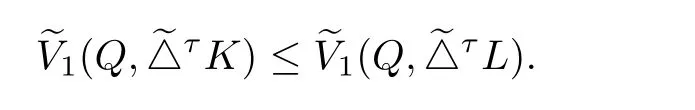
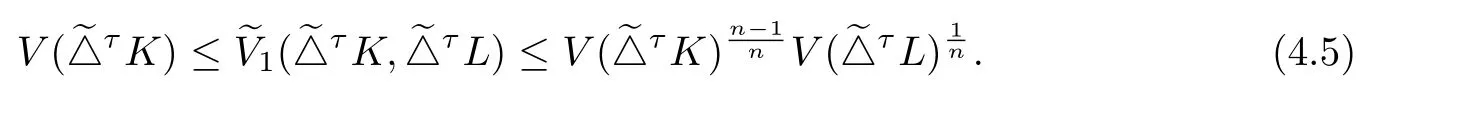
This gives inequality(1.14).
From the equality condition of inequality(2.7),we know that equality holds in(4.5)if and only ife△τK ande△τL are dilates.From this,lete△τK=ce△τL(c>0)in V(e△τK)=V(e△τL),then c=1.This means that equality holds in(1.14)if and only ife△τK=e△τL.
[References]
[1]GARDNER R.J.Geometric Tomography[M].Cambridge:Cambridge Univ Press,2006.
[2]LUTWAK E.Intersection bodies and dual mixed volums[J].Adv Math,1988,71:232-261.
[3]WANG Wei-dong,QI Chen.On isolations for the Brunn-Minkowski inequality of quermassintegrals and dual quermassintegrals[J].Chin Quart J of Math,2012,27(4):582-589.
[4]LUTWAK E.Dual mixed volumes[J].Pacific J Math,1975,58:531-538.
O178,O184Document code:A
date:2014-05-22
Supported by the National Natural Science Foundation of China(11371224);Supported by the Academic Mainstay Foundation of Hubei Pnvince(B2016030)
Biography:ZHANG Ping(1978-),female(Tujiazu),native of Lichuan,Hubei,a lecturer of China Three Gorges University,M.S.D.,engages in convex geometric analysis.
杂志排行
Chinese Quarterly Journal of Mathematics的其它文章
- Growth Theorem and Distortion Theorem for a Subclass of Parabolic Starlike Mappings
- Self-consistent Sources and Conservation Laws for Super-Geng Equation Hierarchy
- Unbounded Motions in Asymmetric Oscillators Depending on Derivatives
- Likelihood Inference under Generalized Hybrid Censoring Scheme with Competing Risks
- LrConvergence for Arrays of Rowwise Negatively Superadditive Dependent Random Variables
- Common Fixed Point Theorems in Non-normal Cone Metric Spaces with Banach Algebras
