Common Fixed Point Theorems in Non-normal Cone Metric Spaces with Banach Algebras

HUANG Hua-ping，XU Shao-yuan，LIU Qiu-hua，MING Wei

（1.School of Mathematical Sciences，Beijing Normal University，Beijing 100875，China；2.Department of Mathematics and Statistics，Hanshan Normal University，Chaozhou 521041，China；3.School of Marxism，Hubei Normal University，Huangshi 435002，China）



Common Fixed Point Theorems in Non-normal Cone Metric Spaces with Banach Algebras

HUANG Hua-ping1，XU Shao-yuan2，LIU Qiu-hua3，MING Wei3

（1.School of Mathematical Sciences，Beijing Normal University，Beijing 100875，China；2.Department of Mathematics and Statistics，Hanshan Normal University，Chaozhou 521041，China；3.School of Marxism，Hubei Normal University，Huangshi 435002，China）

In this paper，we obtain a class of common fixed point theorems for generalized Lipschitz mappings in cone metric spaces with Banach algebras without the assumption of normality of cones.The results greatly generalize some results in the literature.Moreover，we give an example to support the main assertions.

cone metric space with Banach algebra；generalized Lispchitz constant；weakly compatible

2000 MR Subject Classification：47H10，54H25

Article ID：1002—0462（2016）02—0155—07 Chin.Quart.J.of Math. 2016，31（2）：155—161

§1.Introduction

Since Huang and Zhang（see［1］）introduced cone metric spaces，as a generalization of metric spaces，and expanded the famous Banach fixed point theorem，many scholars have focused on fixed point and common fixed point theorems in such spaces（see［2-6］）.But recently，it had not yet been a hot topic since some authors appealed to the equivalence of some metric and cone metric fixed point results（see［7-9］）.Due to these reasons，people begin to lose interest in studying fixed point theorems in cone metric spaces.However，the present situation has gone better since，very recently，Liu and Xu［10］introduced the concept of cone metric space with Banach algebra and obtained some fixed point theorems in such spaces.Moreover，they gave an example to illustrate that the non-equivalence of versions of fixed point theorems between conemetric spaces with Banach algebras and（general）metric spaces（in usual sense），which shows that it is essentially necessary to investigate fixed points in cone metric spaces with Banach algebras.But unfortunately，the main results of［10］have been considered only in such spaces under the condition of normal cones.It is well known that there exist a lot of non-normal cones besides some normal cones（see［6］）.Throughout this paper，we obtain some common fixed point theorems for generalized Lipschitz contractive mappings in cone metric spaces with Banach algebras by deleting the assumptions of normalities of cones.Furthermore，we support our conclusions by an example.

Definition 1.1［10］Let A be a Banach algebra with a unit e and a zero element θ.A nonempty closed convex subset P of A is called a cone if

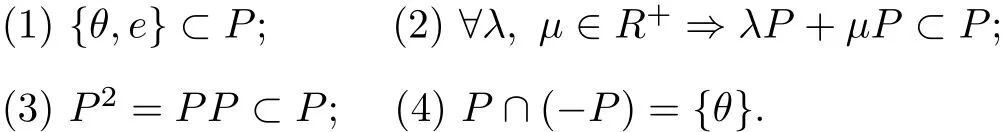
On this basis，we define a partial ordering≤with respect to P by x≤y if and only if y-x∈P.We shall write x≺y to indicate that x≤y but x/=y，while x≪y will indicate that y-x∈intP，where intP stands for the interior of P.If intP/=∅，then P is said to be a solid cone.Write‖·‖as the norm on A.A cone P is called normal if there is a number M＞0 such that for all x,y∈A，θ≤x≤y implies‖x‖≤M‖y‖.The least positive number satisfying above is called the normal constant of P.

In the sequel we always suppose that A is a Banach algebra with a unit e，P is a solid cone in A and≤is a partial ordering with respect to P.

Definition 1.2［1］Let X be a nonempty set and A a Banach algebra.Suppose that the mapping d：X×X→A satisfies

（i）θ≺d（x,y）for all x,y∈X with x/=y and d（x,y）=θ if and only if x=y；（ii）d（x,y）=d（y,x）for all x,y∈X；

（iii）d（x,y）≤d（x,z）+d（z,y）for all x,y,z∈X.

Then d is called a cone metric on X and（X,d）is called a cone metric space with Banach algebra.

Definition 1.3［1］Let（X,d）be a cone metric space，x∈X and｛xn｝a sequence in X. Then

（i）｛xn｝converges to x whenever for every c≫θ there is a natural number N such that d（xn,x）≪c for all n≥N.We denote this by

（ii）｛xn｝is a Cauchy sequence whenever for each c≫θ there is a natural number N such that d（xn,xm）≪c for all n,m≥N.

（iii）（X,d）is a complete cone metric space if every Cauchy sequence is convergent.

Definition 1.4［5］Let f,g：X→X be mappings on a set X.

（i）If y=fx=gx for some x∈X，then x is called a coincidence point of f and g，and y iscalled a point of coincidence of f and g；

（ii）The pair（f,g）is called weakly compatible if f and g commute at all of their coincidence points，that is，fgx=gfx for all x∈C（f,g）=｛x∈X：fx=gx｝.

Lemma 1.5［6］Let A be a Banach algebra and｛an｝a sequence in A.If θ≤an→θ（n→∞），then for each c≫θ，there exists N such that an≪c for all n＞N.

Lemma 1.6［11］Let A be a Banach algebra with a unit e，x∈A，then the limitexists and the spectral radius ρ（x）satisfies

If ρ（x）＜|λ|，then λe-x is invertible in A，moreover，

where λ is a complex constant.

Lemma 1.7［11］Let A be a Banach algebra with a unit e.a,b∈A.If a commutes with b，then

ρ（a+b）≤ρ（a）+ρ（b）,ρ（ab）≤ρ（a）ρ（b）.

Lemma 1.8［4］Let f and g be weakly compatible self maps on a set X.If f and g have a unique point of coincidence y=fx=gx，then y is the unique common fixed point of f and g.

§2.Main Results

Lemma 2.1Let A be a Banach algebra and k∈A.If ρ（k）＜1，then

α＜1.Letting n be big enough，we obtainHence

Lemma 2.2Let A be a Banach algebra with a unit e，｛xn｝a sequence in A.If xnconverges to x in A and for any n≥1，xncommutes with x，then ρ（xn）→ρ（x）as n→∞.

ProofSince xncommutes with x，then it follows by Lemma 1.7 that

thus

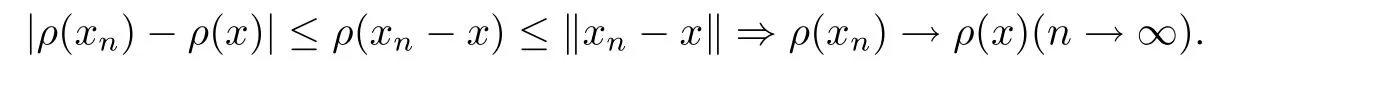
Theorem 2.3Let（X,d）be a cone metric space with Banach algebra A and P be a cone in A.Suppose that the mappings f,g：X→X satisfy the following contractive conditionwhere k∈P is a generalized Lipschitz constant with ρ（k）＜1.If f（X）⊂g（X）and g（X）is a complete subspace of X，then f and g have a unique point of coincidence in X.Moreover，if（f,g）is weakly compatible，then f and g have a unique common fixed point.

ProofLet x0be an arbitrary point in X.Choose a point x1in X such that fx0=gx1. This can be done in view of f（X）⊂g（X）.Continuing this process，having chosen xnin X，we obtain xn+1in X such that fxn=gxn+1.Then

By using Lemma 1.6，for each n＞m，it follows that

Then by Lemma 2.1，one has

which implies that（e-k）-1kmd（gx1,gx0）→θ（m→∞）.So by Lemma 1.5，for each c≫θ，there exists N1such that d（gxn,gxm）≪c for all n＞N1.Hence｛gxn｝is a Cauchy sequence in g（X）.Since g（X）is complete，there is q∈g（X）such that gxn→q（n→∞）.Thus there exists p∈X such that gp=q.Note that gxn-1→q（n→∞），it is easy to see for every real ε＞0，choose c0with θ≪c0and‖k‖‖c0‖＜ε.Then there is N2such that d（gxn-1,q）≪c0for all n＞N2.Consequently，

that is to say gxn→fp（n→∞）.Indeed，owing to

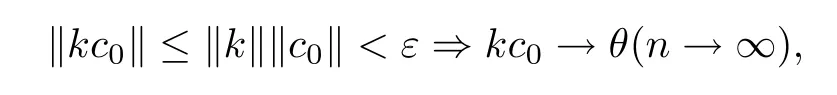
then by Lemma 1.5，for each c≫θ，there exists N3such that d（gxn,fp）≪c for all n＞N3. As a result，gxn→fp（n→∞）.By virtue of gxn→q=gp（n→∞），then fp=gp.In the following we shall prove f and g have a unique point of coincidence.

We suppose for absurd that there exists p0/=p such that fp0=gp0.Then

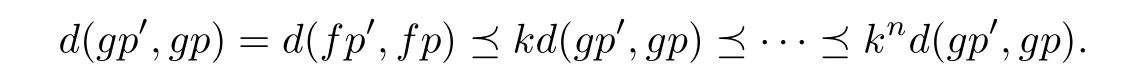
Making use of Lemma 2.1 and the following fact that

we speculate knd（gp0,gp）→θ（n→∞）.So by utilizing Lemma 1.5，one has gp0=gp.Finally，if（f,g）is weakly compatible，then by using Lemma 1.8，we claim that f and g have a unique common fixed point.

Theorem 2.4Let（X,d）be a cone metric space with Banach algebra A and P be a cone in A.Suppose that the mappings f,g：X→X satisfy the following contractive condition：

where k∈P is a generalized Lipschitz constant with ρ（k）＜.If f（X）⊂g（X）and g（X）is a complete subspace of X，then f and g have a unique point of coincidence in X.Moreover，if（f,g）is weakly compatible，then f and g have a unique common fixed point.

ProofLet x0be an arbitrary point in X.Choose a point x1in X such that fx0=gx1. This can be done in view of f（X）⊂g（X）.Continuing this process，having chosen xnin X，we obtain xn+1in X such that fxn=gxn+1.Then

which follows that

where h=（e-k）-1k.Taking advantage of lemmas 1.6 and 2.2，we have

which implies that‖hn‖→0（n→∞）.Following an argument similar to that given in Theorem 2.3，we get that｛gxn｝is a Cauchy sequence in g（X）.Since g（X）is complete，there is q∈g（X）such that gxn→q（n→∞）.Thus there exists p∈X such that gp=q.Note that fxn-1= gxn→q（n→∞），it is easy to see for each c≫θ，there exists N such that d（fxn-1,q）≪c and d（gxn-1,q）≪c for all n＞N.In the meanwhile，based on the fact that

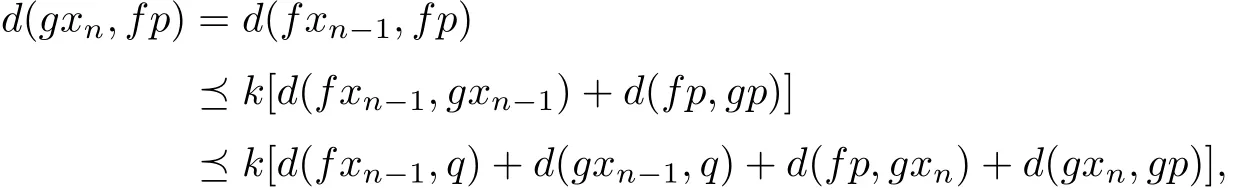
it ensures us that

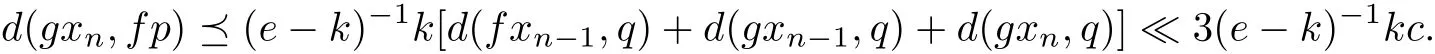
Then gxn→fp（n→∞）.By virtue of gxn→q=gp（n→∞），thus fp=gp.In the following we shall prove f and g have a unique point of coincidence.

If there exists p0/=p such that fp0=gp0.Thenso gp0=gp.Finally，if（f,g）is weakly compatible，then by Lemma 1.8，we claim that f and g have a unique common fixed point.

Theorem 2.5Let（X,d）be a cone metric space with Banach algebra A and P be a cone in A.Suppose that the mappings f,g：X→X satisfy the following contractive condition

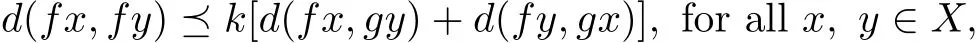
where k∈P is a generalized Lipschitz constant with ρ（k）＜If f（X）⊂g（X）and g（X）is a complete subspace of X，then f and g have a unique point of coincidence in X.Moreover，if（f,g）is weakly compatible，then f and g have a unique common fixed point.

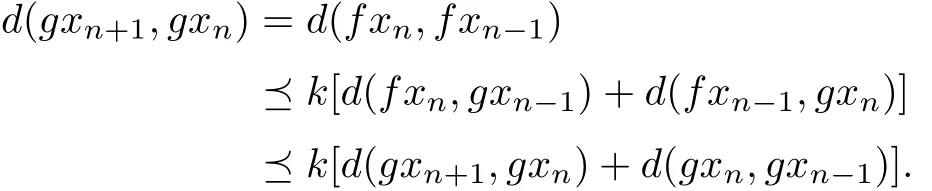
ProofLet x0be an arbitrary point in X.Choose a point x1in X such that fx0=gx1. This can be done in view of f（X）⊂g（X）.Continuing this process，having chosen xnin X，we obtain xn+1in X such that fxn=gxn+1.Then Following an argument similar to that given in Theorem 2.4，we obtain that｛gxn｝is a Cauchy sequence in g（X）.Since g（X）is complete，there is q∈g（X）such that gxn→q（n→∞）. Thus there exists p∈X such that gp=q.Because fxn-1=gxn→q=gp（n→∞）together with｛gxn｝as a Cauchy sequence，it is obvious that for each c≫θ，there exists N such that d（fxn-1,gp）≪c and d（gxn,gxn-1）≪c for all n＞N.Note that ρ（k）＜＜1，then by Lemma 1.6，（e-k）-1exists.Owing to

which establishes that for all n＞N，

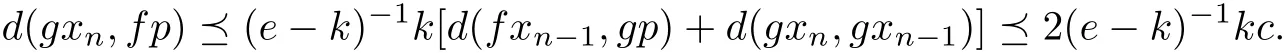
Accordingly，gxn→fp（n→∞）.Then fp=gp=q.In the following we shall prove f and g have a unique point of coincidence.

If there exists p0/=p such that fp0=gp0.Then

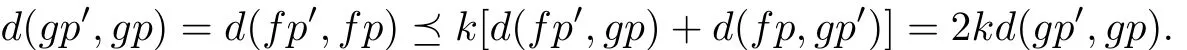
As a result of ρ（2k）=2ρ（k）＜1，using the same way as Theorem 2.3，ones have gp0=gp.In the end，if（f,g）is weakly compatible，then by Lemma 1.8，f and g have a unique common fixed point.

Remark 2.6Theorems 2.3～2.5 expand the main results of［10］.As a matter of fact，if g=I（Identity mapping），then theorems 2.3～2.5 are deduced to theorems 2.1～2.3 of［10］. Further，compared with［10］，our results in this paper discard the normality of cones.

Remark 2.7Theorems 2.3～2.5 greatly generalize the main results of［4］.In fact，on account of ρ（k）=.But the converse is not true.Hence the condition ρ（k）＜1 in Theorem 2.3 is weaker than the condition 0≤k＜1 in Theorem 2.1 of［4］.Similarly，the condition ρ（k）＜in theorems 2.4～2.5 is weaker than the condition 0≤k＜in theorems 2.3～2.4 of［4］.In addition，our assertions delete the normality of cones of［4］.The following example illustrates that our conclusions are reasonable.

Example 2.8Let A=C1R［0,1］and define a norm on A by‖x‖=‖x‖∞+‖x0‖∞.Define multiplication in A as just pointwise multiplication.Then A is a real Banach algebra with a unit e=1（e（t）=1 for all t∈［0,1］）.The set P=｛x∈A：x（t）≥0 for all t∈［0,1］｝is a cone in A.Moreover，P is non-normal solid cone（see［6］）.Let X=｛1,2,3｝.Define d：X×X by d（1,2）（t）=d（2,1）（t）=et,d（2,3）（t）=d（3,2）（t）=2et,d（1,3）（t）=d（3,1）（t）=3etand d（x,x）（t）=θ for all t∈［0,1］and each x∈X.We have that（X,d）is a solid cone metric space with Banach algebra A.Further，let f：X→X be a mapping defined with f1=f2=2,f3=1 and let g：X→X be a mapping defined with g1=1,g2=2,g3=3.Take k∈A such that.By careful calculations one can find the fact that all the conditions of Theorem 2.3 are fulfilled.The point x=2 is the unique common fixed point of f and g.

AcknowledgmentThe authors are greatly thankful to Dr Liu Hao of Hubei Normal University for his valuable suggestions.

［References］

［1］HUANG Long-guang，ZHANG Xian.Cone metric spaces and fixed point theorems of contractive mappings［J］.Journal of Mathematical Analysis and Applications，2007，332：1468-1476.

［2］HUANG Hua-ping，XU Shao-yuan，HAN Yan.Some fixed point results on a class of contractive mappings in cone metric spaces［J］.Chinese Quarterly Journal of Mathematics，2013，28（4）：539-545.

［3］HAN Yan，XU Wang-bin，XU Shao-yuan.Some new theorems of Lipschitz type mappings in cone metric spaces［J］.Chinese Quarterly Journal of Mathematics，2013，28（2）：224-233.

［4］ABBAS M，JUNGCK G.Common fixed point results for noncommuing mappings without continuity in cone metric spaces［J］.Journal of Mathematical Analysis and Applications，2008，341：416-420.

［5］HUSSAIN N，MASSOD H-S，ALIREZA A-H，et al.Common fixed point theorems for generalized contractive mappings with applications［J］.Fixed point theory and applications，2013，169：1-17.

［6］JANKOVI´C S，KADELBURG Z，RADENOVI´C S.On cone metric spaces：a survey［J］.Nonlinear Analysis，2011，74：2591-2601.

［7］KADELBURG Z，RADENOVI´C S，RAKOˇCEVI´C V.A note on the equivalence of some metric and cone metric fixed point results［J］.Applied Mathematics Letters，2011，24：370-374.

［8］ASADA M，RHOADES B-E，SOLEIMANI H.Some notes on the paper“The equivalence of cone metric spaces and metric spaces”［J］.Fixed Point Theory and Applications，2012，87：1-4.

［9］ERCAN Z.On the end of the cone metric spaces［J］.Topology and Its Applications，2014，166：10-14.

［10］LIU Hao，XU Shao-yuan.Cone metric spaces with Banach algebras and fixed point theorems of generalized Lipschitz mappings［J］.Fixed Point Theory and Applications，2013，320：1-10.

［11］RUDIN W.Functional Analysis［M］.New York，NY，USA：McGraw-Hill，1991.

O177.91Document code：A

date：2014-04-14

Supported by the Science and Technology Research Project of the Education Department of Hubei Province（B2015137）；Supported by the National Social Science Foundation of China（12BZS050）

Biography：HUANG Hua-ping（1978-），male，native of Anlu，Hubei，an associate professor of Hubei Normal University，engages in nonlinear analysis.