LrConvergence for Arrays of Rowwise Negatively Superadditive Dependent Random Variables

ZHU Hua-yan，SHEN Ai-ting，ZHANG Ying

（School of Mathematical Sciences，Anhui University，Hefei 230601，China）



LrConvergence for Arrays of Rowwise Negatively Superadditive Dependent Random Variables

ZHU Hua-yan，SHEN Ai-ting，ZHANG Ying

（School of Mathematical Sciences，Anhui University，Hefei 230601，China）

Let｛Xnk，k≥1，n≥1｝be an array of rowwise negatively superadditive dependent random variables and｛an，n≥1｝be a sequence of positive real nfulmbers sfluch that an↑∞.Under some suitable conditions，Lrconvergence of

Lrconvergence；convergence in probability；negatively superadditive dependent random variables

Chin.Quart.J.of Math.

2016，31（2）：162—170

§1.Introduction

Recently，Gan and Chen［1］obtained the following results of convergence in probability for arrays of rowwise negatively associated（NA，in short）random variables.

Theorem ALet｛Xnk,k≥1,n≥1｝be an array of rowwise NA random variables，｛an,n≥1｝a sequence of positive real numbers with an↑∞，and｛Ψk（t）,k≥1｝a sequence ofnonnegative even functions such that Ψk（t）＞0 for t＞0 and

where 1＜p≤2.Assume further that

and

then

The main purpose of this paper is to generalize and improve the result of Theorem A for arrays of rowwise NA random variables to the case of negatively superadditive dependent settings，which includes NA as a special case.Especially，we will consider the Lrconvergence for negatively superadditive dependent random variables，which is stronger than convergence in probability.

The concept of negatively superadditive dependent random variables was introduced by Hu［2］as follows.

Definition 1.1［3］A function φ：Rn→R is called superadditive if φ（x∨y）+φ（x∧y）≥φ（x）+φ（y）for all x,y∈Rn，where∨is for componentwise maximum and∧is for componentwise minimum.

Definition 1.2［2］A random vector X=（X1,X2,···,Xn）is said to be negatively superadditive dependent（NSD，in short）if

A sequence｛Xn,n≥1｝of random variables is said to be NSD if for every n≥1，（X1,X2,···,Xn）is NSD.

An array｛Xni,i≥1,n≥1｝of random variables is said to be rowwise NSD if for all n≥1，｛Xni,i≥1｝is NSD.

The concept of NSD random variables was introduced by Hu［2］.He gave an example illustrating that NSD does not imply negative association（NA，in short，see［4-12］for instance），and posed an open problem whether NA implies NSD.Christofides and Vaggelatou［13］solved this open problem and indicated that NA implies NSD.Negatively superadditive dependent structure is an extension of negatively associated structure and sometimes more useful than it and can be used to get many important probability inequalities and moment inequalities.For more details about NSD random variables，one can refer to Eghbal et al［1415］，Wang et al［1618］，Shen［19］，Shen et al［20］and so on.

Throughout this paper，the symbol C always stands for a generic positive constant，which may vary from one place to another and dxe denotes the integer part of x.Let｛Xnk,k≥1,n≥1｝be an array of rowwise NSD random variables with the mixing coefficients｛un,n≥1｝in each row.Let｛an,n≥1｝be a sequence of positive real numbers such that an↑∞and let｛Ψk（t）,k≥1｝be a sequence of positive even functions such that

for some 1≤q＜p and each k≥1.

We point out that Theorem A only considers the case q=1，while this work will consider the case q≥1.In addition，we will improve the result of convergence in probability to the case of Lrconvergence.Please see Theorem 3.1 below.

There are many examples of function Ψk（t）satisfying condition（1.6），such as Ψk（t）=|t|βfor some q＜β＜p，Ψk（t）=|t|qlog（1+|t|p-q）for t∈（-∞,+∞），and so forth.Note that under condition（1.6），the function Ψk（t）is an increasing function for t＞0.

§2.Preliminary Lemmas

To prove the main results，we need the following important lemmas.The first one is a basic property for NSD random variables，which was given by Hu［2］.

Lemma 2.1Let（X1,X2,···,Xn）be NSD.

（i）（-X1,-X2,···,-Xn）is also NSD.

（ii）If g1,g2,···,gnare all nondecreasing functions，then（g1（X1）,g2（X2）,···,gn（Xn））is NSD.

The next one is the moment inequality for NSD random variables，which was obtained by Wang et al［17］.

Lemma 2.2Let p＞1.Let｛Xn,n≥1｝be a seuqnce of mean zero NSD random variables with E|Xi|p＜∞for each i≥1.Then for all n≥1，

and

The following lemma plays an important role to prove our main results.

Lemma 2.3Let｛Xnk,k≥1,n≥1｝be an array of random variables.Let｛an,n≥1｝be a sequence of positive real numbers such that an↑∞and｛Ψk（t）,k≥1｝be a positive even function satisfying（1.6）for 1≤q＜p and p＞2.Then（1.3）implies the following statements.

（i）For 0＜u≤q，

（ii）For v≥p，

ProofIt follows from（1.3）and（1.6）that

and

which imply（i）and（ii），respectively.

By（i），we can get that

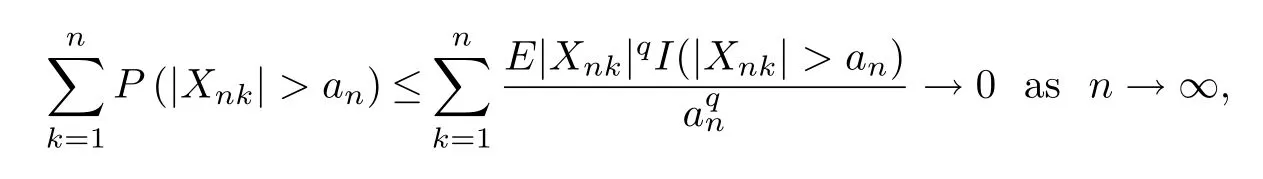
which implies（iii）.This completes the proof of the lemma.

§3.Main Result and Its Proof

Our main result is as follows.

Theorem 3.1Let｛Xnk,k≥1,n≥1｝be an array of rowwise NSD random variables. Let｛an,n≥1｝be a sequence of positive real numbers such that an↑∞and｛Ψk（t）,k≥1｝be a positive even function satisfying（1.6）for 1≤q＜p≤2.Then under conditions（1.2）and（1.3），we have

ProofFor n≥1，denote Mn（X）=It is easy to check that for any ε＞0，

In view of the arbitrariness of ε＞0，we only need to show In→0 as n→∞.

Without loss of generality，we may assume that 0＜ε＜1.For fixed n≥1，we denote for 1≤k≤n that Ynk=-t1/qI（Xnk＜-t1/q）+XnkI（|Xnk|≤t1/q）+t1/qI（Xnk＞t1/q）, Znk=Xnk-Ynk

and Mn（Y）=.Obviously，

Hence，

For In1，we have by Markov's inequality and（2.1）～（2.2）that

Next，we will prove that In2→0 as n→∞.It follows from（1.2），（2.1）and（2.2）that

which implies that for n sufficiently large，

Hence，we have for n sufficiently large that

Let dn=dane+1.Noting that for fixed n≥1，｛Ynk-EYnk,1≤k≤n｝are NSD with mean zero by Lemma 2.1.By using（3.6），Markov's inequality and Lemma 2.2，we have

To prove In2→0 as n→∞，it suffices to show that In21→0 and In22→0 as n→∞.For In21，since q＜2，we have

By（2.2），we can see that H1→0 as n→∞since p≤2.Now we prove that H2→0 as n→∞. Since q＜2 and（an+1）/an→1 as n→∞，it follows from（2.1）that

which together with H1→0 as n→∞yield that In21→0 as n→∞. Finally，we will prove that In22→0 as n→∞.Noting that

we have

Let t=uqin In22.Since 1≤q＜2，we have

Combining above analysis with（2.1），we have

Hence，In→0 as n→∞follows by（3.3），（3.4），（3.7）～（3.9）immediately，which together with（3.2）yields the desired result（3.1）by letting ε↓0.This completes the proof of the theorem.

Remark 3.1Comparing with Theorem A，we have the following generalizations or improvements.

（1）Theorem A only considers the case q=1，while Theorem 3.1 considers the case 1≤q＜2.

（2）The array of rowwise NA random variables is extended to the case of array of rowwise NSD random variables.

（3）（3.1）implies（1.4）.

AcknowledgementThe authors are most grateful to the Editor and anonymous referees for careful reading of the manuscript and valuable suggestions which helped in significantly improving an earlier version of this paper.

［1］GAN Shi-xin，CHEN Ping-yan.On the limiting behavior of the maximum partial sums for arrays of rowwise NA random variables［J］.Acta Mathematica Scientia，2007，27B（2）：283-290.

［2］HU Tai-zhong.Negatively superadditive dependence of random variables with applications［J］.Chinese Journal of Applied Probability and Statistics，2000，16：133-144.

［3］KEMPERMAN J H B.On the FKG-inequalities for measures on a partially ordered space［J］.Indagationes Mathematicae，1977，80：313-331.

［4］ALAM K，SAXENA K M L.Positive dependence in multivariate distributions［J］.Communications in Statistics-Theory and Methods，1981，10：1183-1196.

［5］JOAG-DEV K，PROSCHAN F.Negative association of random variables with applications［J］.Annals of Statistics，1983，11（1）：286-295.

［6］MATULA P.A note on the almost sure convergence of sums of negative dependent random variables［J］. Statistics and Probability Letters，1992，15：209-213.

［7］SHAO Qi-man.A comparison theorem on moment inequalities between negatively associated and independent random variables［J］.Journal of Theoretical Probability，2000，13：343-356.

［8］WU Qun-ying.Probability Limit Theory for Mixing Sequences［M］.Beijing：Science Press of China，2006.

［9］WU Qun-ying，JIANG Yuan-ying.Chover's law of the iterated logarithm for negatively associated sequences［J］.Journal of Systems Science and Complexity，2010，23：293-302.

［10］WU Qun-ying，JIANG Yuan-ying.A law of the iterated logarithm of partial sums for negatively associated random variables［J］.Journal of the Korean Statistical Society，2010，39：199-206.

［11］WANG Xue-jun，LI Xiao-qin，HU Shu-he，et al.Strong limit theorems for weighted sums of negatively associated random variables［J］.Stochastic Analysis and Applications，2011，29（1）：1-14.

［12］ZHOU Xin-cai，HU Shu-he.Some asymptotic properties for multivariate partially linear models［J］.Chinese Quarterly Journal of Mathematics，2011，26（1）：270-274.

［13］CHRISTOFIDES T C，VAGGELATOU E.A connection between supermodular ordering and positive/negative association［J］.Journal of Multivariate Analysis，2004，88：138-151.

［14］EGHBAL N，AMINI M，BOZORGNIA A.Some maximal inequalities for quadratic forms of negative superadditive dependence random variables［J］.Statistics and Probability Letters，2010，80：587-591.

［15］EGHBAL N.，AMINI M，BOZORGNIA A.On the Kolmogorov inequalities for quadratic forms of dependent uniformly bounded random variables［J］.Statistics and Probability Letters，2011，81：1112-1120.

［16］WANG Xue-jun，HU Shu-he，YANG Wen-zhi.Some convergence results for arbitrary sequences under moment condition［J］.Chinese Quarterly Journal of Mathematics，2011，26（4）：585-589.

［17］WANG Xue-jun，DENG Xin，ZHENG Lu-lu，et al.Complete convergence for arrays of rowwise negatively superadditive-dependent random variables and its applications［J］.Statistics：A Journal of Theoretical and Applied Statistics，2014，48（4）：834-850.

［18］WANG Xue-jun，SHEN Ai-ting，CHEN Zhi-yong，et al.Complete convergence for weighted sums of NSD random variables and its application in the EV regression model［J］.TEST，2015，24：166-184.

［19］SHEN Ai-ting，ZHANG Ying，VOLODIN A.Applications of the Rosenthal-type inequality for negatively superadditive dependent random variables［J］.Metrika，2015，78（3）：295-311.

［20］SHEN Yan，WANG Xue-jun，YANG Wen-zhi，et al.Almost sure convergence theorem and strong stability for weighted sums of NSD random variables［J］.Acta Mathematica Sinica（English Series），2013，29（4）：743-756.

O211.4Document code：A

1002—0462（2016）02—0162—09

Received date：2014-04-18

Foundation item：Supported by the Provincial Natural Science Research Project of Anhui Colleges（KJ2015 A018）；Supported by the Students Science Research Training Program of Anhui University（kyxl2013003）；Supported by the Students Innovative Training Project of Anhui University（201410357118）；Supported by the Quality Engineering Project of Anhui Province（2015jyxm045）；Supported by the Quality Improvement Project for Undergraduate Education of Anhui University（ZLTS2015035）

Biographies：ZHU Hua-yan（1994-），male，native of Hefei，Anhui，engages in probability limit theorem；SHEN Ai-ting（1979-），female，native of Hefei，Anhui，an associate professor of Anhui Universiry，Ph.D.，engages in probability limit theorem；ZHANG Ying（1993-），female，native of Putian，Fujian，engages in probability limit theorem.

studied.The results obtained in this paper generalize and improve some corresponding ones for negatively associated random variables and independent random variables.

2000 MR Subject Classification：60F15，60F05