Distance Integral Complete Multipartite Graphs with s=5,6

YANG Ruo-song，WANG Li-gong

（School of Science，Northwestern Polytechnical University，Xi’an 710072，China）



Distance Integral Complete Multipartite Graphs with s=5,6

YANG Ruo-song，WANG Li-gong

（School of Science，Northwestern Polytechnical University，Xi’an 710072，China）

Chin.Quart.J.of Math.

2016，31（2）：111—117

Let D（G）=（dij）n×ndenote the distance matrix of a connected graph G with order n，where dijis equal to the distance between vertices viand vjin G.A graph is called distance integral if all eigenvalues of its distance matrix are integers.In 2014，Yang and Wang gave a sufficient and necessary condition for complete r-partite graphs Kp1,p2,···,pr= Ka1·p1,a2·p2,···,as···psto be distance integral and obtained such distance integral graphs with s=1，2，3，4.However distance integral complete multipartite graphs Ka1·p1,a2·p2,···,as·pswith s＞4 have not been found.In this paper，we find and construct some infinite classes of these distance integral graphs Ka1·p1,a2·p2,···,as·pswith s=5，6.The problem of the existence of such distance integral graphs Ka1·p1,a2·p2,···,as·pswith arbitrarily large number s remains open.

complete multipartite graph；distance matrix；distance integral；graph spectrum

2000 MR Subject Classification：05C50，05C12

Article ID：1002—0462（2016）02—0111—07

§1.Introduction

Let G be a simple connected undirected graph with vertexset denotedbyV（G）=｛v1,v2,···, vn｝.A（G）=（aij）is an n×n matrix，where aij=1 if viand vjare adjacent and aij=0 otherwise.The distance between the vertices viand vjis the length of a shortest path between them，and is denoted by dij.The distance matrix of G，denoted by D（G），is the n×n matrix whose（i,j）-entry is equal to dijfor i,j=1,2,···,n（see［3］）.Note that dii=0，i=1,2,···,n.Thedistance characteristic polynomial（or D-polynomial）of G is DG（x）=|xIn-D（G）|，where Inis the n×n identity matrix.The eigenvalues of D（G）are said to be the distance eigenvalues or D-eigenvalues of G.Since D（G）is a real symmetric matrix，the D-eigenvalues are real and can be denoted asµ1≥µ2≥···≥µn.The distance spectral radius of G is the largest D-eigenvalue µ1and denoted byµ（G）.Assume thatµ1＞µ2＞···＞µtare t distinct D-eigenvalues of G with the corresponding multiplicities k1,k2,···,kt.We denote by Spec（G）=the Distance spectrum or the D-spectrum of G.G is called integral if all eigenvalues of A（G）are integers.Similarly to integral graphs，a graph is called distance integral if all its D-eigenvalues are integers.Many results about distance spectral radius and the D-eigenvalues of graphs can be found in［1，2，4，6-7，9，11-12，15，17-18］.Some more results about spectral graph theory can be found in［8，13，19］.

A complete r-partite（r≥2）graph Kp1,p2,···,pris a graph with a set V=V1∪V2∪···∪Vrof p1+p2+···+pr（=n）vertices，where Vi's are nonempty disjoint sets|Vi|=pi，such that two vertices in V are adjacent if and only if they belong to different Vi's.Assume that the number of distinct integers of p1,p2,···,pris s.Without loss of generality，assume that the first s ones are the distinct integers such that p1＜p2＜···＜ps.Suppose that aiis the multiplicity of pifor each i=1,2,···,s.The complete r-partite graph Kp1,p2,···,pr=Kp1,···,p1,···,ps,···,pson n vertices is also denoted by Ka1·p1,a2·p2,···,as·ps，where r=and n=aipi.In 2014， Yang and Wang gave a sufficient and necessary condition for Ka1·p1,a2·p2,···,as·psto be distance integral and obtained such distance integral graphs Ka1·p1,a2·p2,···,as·pswith s=1,2,3,4（see［16］）.In this paper，we find and construct some infinite classes of these distance integral graphs Ka1·p1,a2·p2,···,as·pswith s=5,6 by using a computer search.For s=5,6，we give a positive answer to a question of Yang et al［16］.The problem of the existence of distance integral complete multipartite graphs Ka1·p1,a2·p2,···,as·pswith arbitrarily large number s remains open.

§2.Preliminaries

In this section，we shall give some known results on distance integral complete r-partite graphs，which are used in our theorem proof later.

Theorem 1（See Theorem 4.1 of［7］and［10］）Let G be a complete r-partite graph Kp1,p2,···,pron n vertices.Then the D-polynomial of G is

Theorem 2（See［16］）If the complete r-partite graph Kp1,p2,···,pr=Ka1·p1,a2·p2,···,as·pson n vertices is distance integral then there exist integersµi（i=1,2,···,s）such that-2＜p1-2＜µ1＜p2-2＜µ2＜···＜ps-1-2＜µs-1＜ps-2＜µs＜+∞and the numbers a1,a2,···,asdefined byare positive integers.

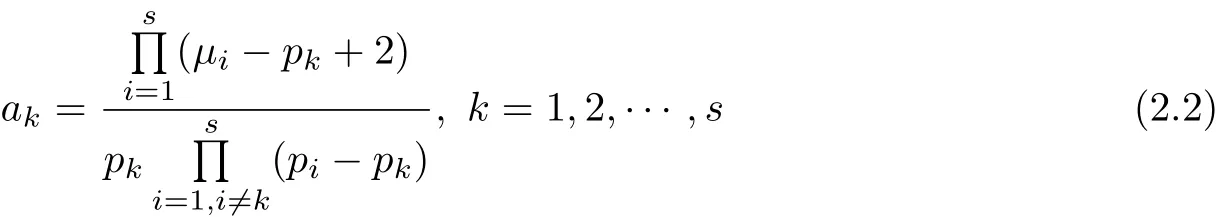
Conversely，suppose that there exist integersµi（i=1,2,···,s）such that-2＜p1-2＜µ1＜p2-2＜µ2＜···＜ps-1-2＜µs-1＜ps-2＜µs＜+∞and that the numbersare positive integers.Then the complete r-partite graph Kp1,p2,···,pr=Ka1·p1,···,as·psis distance integral.

Theorem 3（See Corollary 2.9 of［16］）For any positive integer q，the complete r-partite graph Kp1q,p2q,...,prq=Ka1·p1q,a2·p2q,···,as·psqis distance integral if and only if the complete rpartite graph Kp1,p2,···,pr=Ka1·p1,a2·p2,···,as·psis distance integral.

Remark 4Let GCD（p1,p2,···,ps）denote the greatest common divisor of the numbers p1,p2,···,ps.We say that a vector（p1,p2,···,ps）is primitive if GCD（p1,p2,···,ps）=1. Theorem 3 shows that it is reasonable to study the complete r-partite graph Kp1,p2,···,pr= Ka1·p1,a2·p2,···,as·psonly for primitive vectors（p1,p2,···,ps）.

Theorem 5（See［16］）Let a complete r-partite graph Kp1,p2,···,pr=Ka1·p1,a2·p2,···,as·psbe distance integral with eigenvaluesµi.Letµi（≥0）and pi（＞0）（i=1,2,···,s）be integers such that-2＜p1-2＜µ1＜p2-2＜µ2＜···＜ps-1-2＜µs-1＜ps-2＜µs＜+∞and

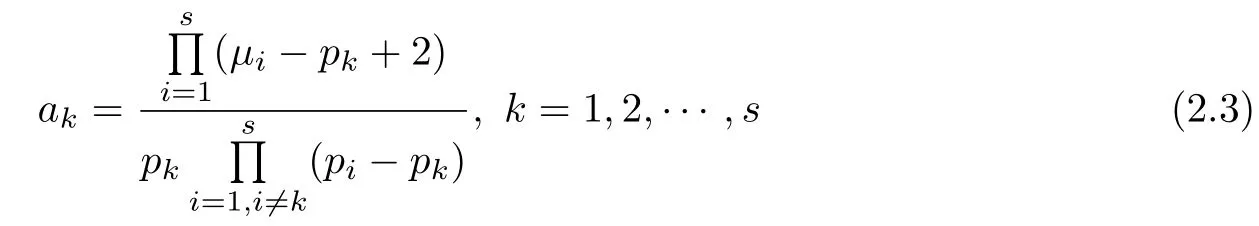
are positive integers，then for

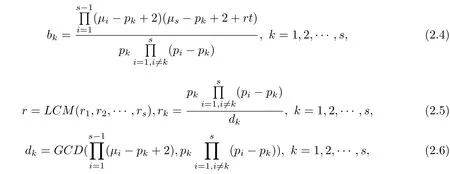
the complete m-partite graph Kp1,p2,···,pm=Kb1·p1,b2·p2,···,bs·psis distance integral for every nonnegative integer t with eigenvaluesµ1,µ2,···,µs-1,µ0s=µs+rt（similar results for integral complete multipartite graphs were given in［5］）.

§3.Main Results

In this section，we construct some distance integral complete r-partite graphs with s=5,6. Moreover we also get infinitely many new classes of distance integral complete r-partite graphs Kp1,p2,···,pr=Ka1·p1,a2·p2,···,as·pswith s=5,6 by using Theorem 5（similar results for integral complete multipartite graphs were given in［14］）.

Theorem 6For s=5，integers pi（＞0），ai（＞0）andµi（i=1,2,3,4,5）are given in Table 1.pi，aiandµi（i=1,2,3,4,5）are those of Theorem 2，where GCD（p1,p2,p3,p4,p5）=1.Then for any positive integer q the graph Ka1·p1q,a2·p2q,a3·p3q,a4·p4q,a5·p5qonvertices is distance integral.

ProofFrom Theorem 2，it is not difficult to find that for s=5 the complete r-partite graphs Kp1,p2,···,pr=Ka1·p1,a2·p2,···,as·psis distance integral if and only if integers pi（＞0），ai（＞0）andµi（i=1,2,3,4,5）satisfy the following equations.

From Theorem 3，we need only consider the case GCD（p1,p2,···,ps）=1.Hence，by using a computer search，we have found 37 integral solutions listed in Table 1，where 1≤p1≤7, p1+1≤p2≤15,p2+1≤p3≤20,p3+1≤p4≤24,p4+1≤p5≤50,p1-2＜µ1＜p2-2， p2-2＜µ2＜p3-2，p3-2＜µ3＜p4-2，p4-2＜µ4＜p5-2，µ5＜10000 and n=

By Theorem 3 it follows that these graphs Ka1·p1q,a2·p2q,a3·p3q,a4·p4q,a5·p5qare distance integral for any positive integer q.

According to theorems 3 and 5，we can obtain the following theorem.

Theorem 7For s=5，let pi（＞0），ai（＞0）andµi（＞0）（i=1,2,3,4,5）be those of Theorem 2.Then for any positive integer q，the complete multipartite graphs Ka1·p1q,a2·p2q,···,a5·p5qwithvertices are distance integral if p1=1，p2=4，p3=8,p4=18， p5=31，µ1=1，µ2=5，µ3=14，µ4=20，µ5=9298+13236132t，a1=4671576t+3282, a2=472719t+332，a3=143871t+101，a4=31372t+22，a5=159936t+112 andi=324632t+2622，where t is a nonnegative integer.

ProofThe proof directly follows from theorems 3 and 5.

Remark 8Analogously to Theorem 7 it is possible to find conditions for parameters pi，ai（i=1,2,3,4,5）which depend on t for each graph in Table 1.By this procedure we get new classes of distance integral graphs.

Theorem 9For s=6，let p1=2，p2=5，p3=11，p4=18，p5=21，p6=23，µ1=1，µ2=7，µ3=12，µ4=18，µ5=20，µ6=53979，a1=4735，a2=2941，a3=514，a4=593，a5=213，a6=391.Then for any positive integer q the graph Ka1·p1q,a2·p2q,a3·p3q,a4·p4q,a5·p5q,a6·p6qvertices is distance integral.

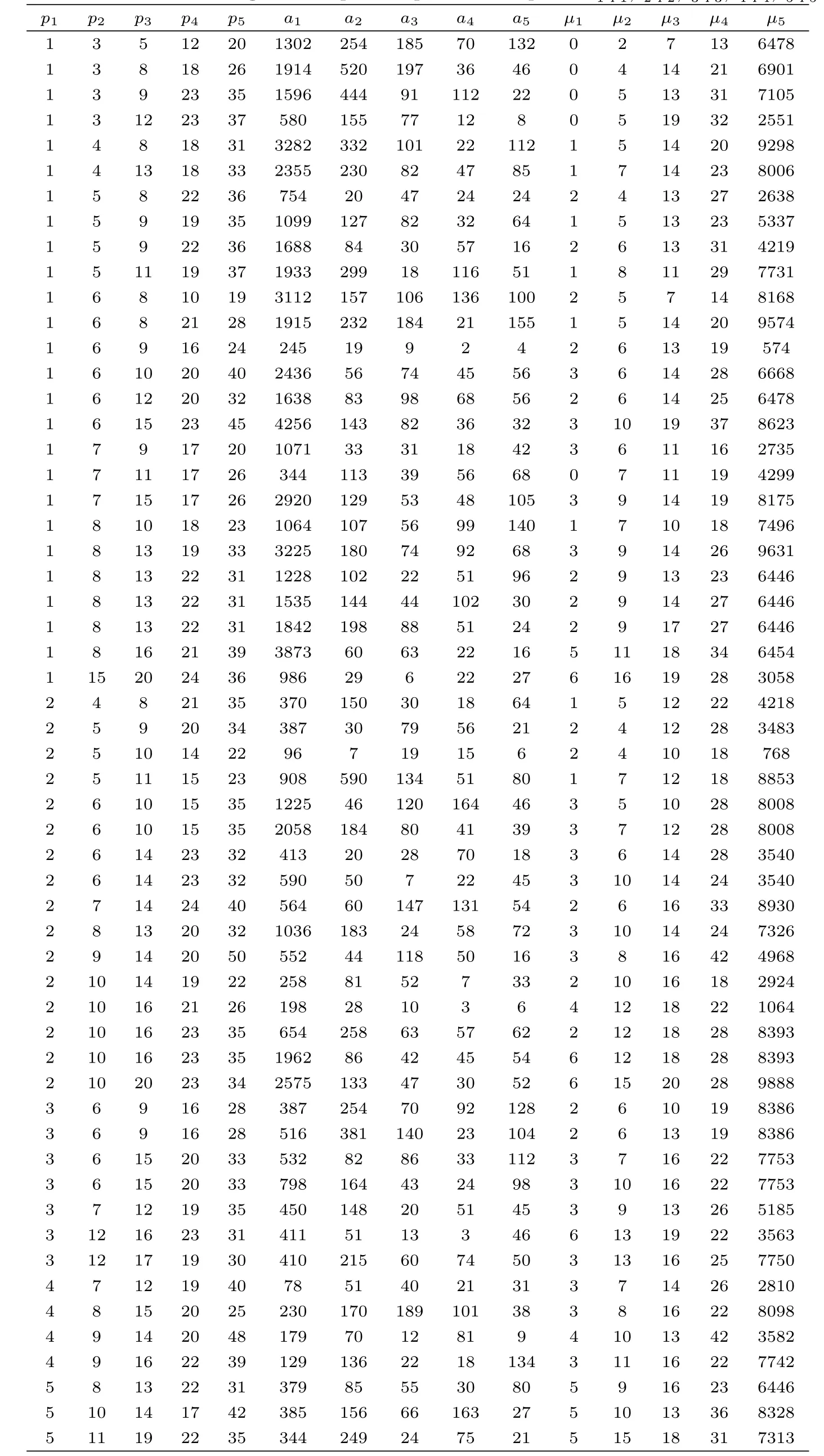
Table 1Distance Integral Complete r-partite Graphs Ka1·p1,a2·p2,a3·p3,a4·p4,a5·p5

ProofFrom Theorem 2，it is not difficult to find that for s=6 the complete r-partite graphs Kp1,p2,···,pr=Ka1·p1,a2·p2,···,as·psis distance integral if and only if integers pi（＞0），ai（＞0）andµi（i=1,2,3,4,5,6）satisfy the following equations.

From Theorem 3，we need only consider the case GCD（p1,p2,···,ps）=1.Hence，by using a computer search，we found this result，where 1≤p1≤5,p1+1≤p2≤p1+10, p2+1≤p3≤p2+10,p3+1≤p4≤p3+10,p4+1≤p5≤p4+10,p5+1≤p6≤p5+20, p1-2＜µ1＜p2-2，p2-2＜µ2＜p3-2，p3-2＜µ3＜p4-2，p4-2＜µ4＜p5-2， p5-2＜µ5＜p6-2，p6-2＜µ6＜200000 and n=

By Theorem 3 it follows that these graphs Ka1·p1q,a2·p2q,a3·p3q,a4·p4q,a5·p5q,a6·p6qare distance integral for any positive integer q.

According to theorems 3 and 5，we can obtain the following theorem.

Theorem 10For s=6，let pi（＞0），ai（＞0）andµi（＞0）（i=1,2,3,4,5,6）be those of Theorem 2.Then for any positive integer q，the complete multipartite graphs Ka1·p1q,a2·p2q,a3·p3q,...,a5·p5q,a6·p6qwith qnvertices are distance integral if p1=2，p2=5，p3=11, p4=18，p5=21，p6=23，µ1=1，µ2=7，µ3=12，µ4=18，µ5=20，µ6=9598038t+53979，a1=418600t+4735,a2=260015t+2941，a3=45448t+514，a4=52440t+593，a5= 18837t+213，a6=34580t+391=829920t+9387，where t is a nonnegative integer.

ProofThe proof directly follows from theorems 3 and 5.

［References］

［1］AOUCHICHE M，HANSEN P.Two Laplacians for the distance matrix of a graph［J］.Linear Algebra Appl，2013，439：21-33.

［2］BOSE S S，NATH M，PAUL S.Distance spectral radius of graphs with r pendent vertices［J］.Linear Algebra Appl，2011，435：2828-2836.

［3］BUCKLEY F，HARARY F.Distance in Graphs［M］.Redwood City：Addison-Wesley Publishing Company，1990.

［4］DAS K C.On the largest eigenvalue of the distance matrix of a bipartite graph［J］.MATCH Commun Math Comput Chem，2009，62：667-672.

［5］H´IC P，POKORN´Y M.New classes of integral complete n-partite graphs［J］.Advances and Applications in Discrete Mathematics，2011，7（2）：83-94.

［6］INDULAL G，GUTMAN I.On the distance spectra of some graphs［J］.Math Commun，2008，13：123-131.

［7］LIN Hui-qiu，YUAN Hong，WANG Jian-feng，et al.On the distance spectrum of graphs［J］.Linear Algebra Appl，2013，439：1662-1669.

［8］LU Shi-fang，ZHAO Hai-xing.Signless Laplacian characteristic polynomials of complete multipartite graphs［J］. Chinese Quarterly Journal of Mathematics，2012，27（1）：36-40.

［9］MERRIS R.The distance spectrum of a tree［J］.J Graph Theory，1990，14：365-369.

［10］STEVANOVI´C D，MILOSEVI´C M，H´IC P，et al.Proof of a conjecture on distance energy of complete multipartite graphs［J］.MATCH Commun Math Comput Chem，2013，70：157-162.

［11］STEVANOVI´C D，ILI´C A.Distance spectral radius of trees with fixed maximum degree［J］.Electron J Linear Algebra，2010，20：168-179.

［12］STEVANOVI´C D，INDULAL G.The distance spectrum and energy of the compositions of regular graphs［J］. Appl Math Lett，2009，22：1136-1140.

［13］TAN Shang-wang.On the Laplacian spectral radius of trees［J］.Chinese Quarterly Journal of Mathematics，2010，25（4）：615-625.

［14］WANG Li-gong，WANG Qi.Integral complete multipartite graphs Ka1·p1,a2·p2,···,as·pswith s=5，6［J］. Discrete Math，2010，310：812-818.

［15］WANG Yan-na，ZHOU Bo.On distance spectral radius of graphs［J］.Linear Algebra Appl，2013，438：3490-3503.

［16］YANG Ruo-song，WANG Li-gong.Distance integral complete r-partite graphs［J］.Filomat，2015，29（4）：739-749.

［17］ZHOU Bo.On the largest eigenvalue of the distance matrix of a tree［J］.MATCH Commun Math Comput Chem，2007，58：657-662.

［18］ZHOU Bo，ILI´C A.On distance spectral radius and distance energy of graphs［J］.MATCH Commun Math Comput Chem，2010，64：261-280.

［19］ZHOU Hou-qing.The rank of integral circulant graphs［J］.Chinese Quarterly Journal of Mathematics，2014，29（1）：116-124.

O157.5Document code：A

date：2015-02-10

Supported by the National Natural Science Foundation of China（11171273）；Supported by the Graduate Starting Seed Fund of Northwestern Polytechnical University（Z2014173）

Biographies：YANG Ruo-song（1990-），male，native of Luoyang，Henan，an postgraduate student of Northwestern Polytechnical University，engages in graph theory and its applications；WANG Li-gong（corresponding author）（1968-），male，native of Xinzhou，Shanxi，a professor of Northwestern Polytechnical University，Ph.D.，engages in graph theory and its applications.