Exact Solutions of the Wick-type KdV-Burgers Equation
2016-09-15LIUShaoqingGAOGuocheng
LIU Shao-qing,GAO Guo-cheng
(Department of Basic Courses,Shandong University of Science and Technology,Jinan 250031,China)
Exact Solutions of the Wick-type KdV-Burgers Equation
LIU Shao-qing,GAO Guo-cheng
(Department of Basic Courses,Shandong University of Science and Technology,Jinan 250031,China)
In this paper,we consider the wick-type KdV-Burgers equation with variable coefficients.By using Tanh method with the aid of Hermite transformation,we deduce the exact solutions which include hyperbolic-exponential,trigonometric-exponential and exponential function solutions for the considered equation.
stochastic partial differential equation;Tanh method;exact solutions
2000 MR Subject Classification:35Q20
Article ID:1002—0462(2016)02—0139—08
Chin.Quart.J.of Math.
2016,31(2):139—146
§1.Introduction
In the 1980s,Wadati[13]first introduced and studied stochastic KdV equations.From then on,more and more scholars begin to pay close attention to this kind of equation and get a lot of valuable research results[49].Compared with other partial differential equation,the solutions of the stochastic partial differential equations(SPDEs)are more difficult to find.Since 1996,Holden et al[10]has studied Wick stochastic partial differential equation using white noise analysis.Then more and more researches about the exact solution of the SPDEs appear.In 2003,Xie[11]studied stochastic KdV equation with the homogeneous balance method to obtain a lot of random solitary wave solution and then used the same method to study stochastic mKdV equations,stochastic Kadomtsev-Petviashvili equation and 2-dimension stochastic KdV equations[1214].Subsequently,Chen et al[1516]studied the generalized stochastic Hirota-Satsuma and stochastic nonlinear Schr¨odinger equation with F-expansion method.Liu and others[1719]studied stochastic mKdV equations and stochastic KdV equation by mapping method.In 2007,Liu[20]studied the stochastic KdV equations using Jacobi ellipticfunction method,then studied the generalized stochastic KdV equations using Tanh function method[21].Kim and others[22]studied generalized stochastic Boussinesq equations and stochastic Kadomtsev-Petviashvili equation with-expansion method.
In this paper,we will deduce three types of the exact solutions to the generalized stochastic KdV-Burgers equation
Ut+H1(t)ƒ(Uxxx+6U ƒ Ux)+4H2(t)ƒ Ux-H3(t)ƒ(2U+xUx)+H4(t)ƒ Uxx=0,(1.1)where ƒ stands for the Wick product on the Hida distribution space(S(R))∗and Hi(t)(i= 1,2,3)are the white noise.
§2.Theoretic Foundation
Let(S(Rd))and(S(Rd))∗be the Hida test function space and the Hida distribution space on Rd.We first introduce some concepts about the Wick type.The Wick product X ƒ Y of two elementsis defined by X ƒ Y=
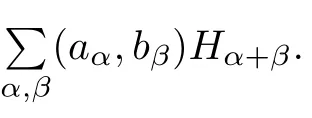
Suppose that modeling considerations lead us to consider an SPDE expressed formally as

where A is some given function,U=U(t,x,ω)is the unknown(generalized)stochastic process, and where the operatorswhen x=(x1,x2,···,xd)∈Rd.
First we interpret all products as Wick products and all functions as their Wick versions,We indicate this as

Secondly,we take the Hermite transform of(2.2).This turns Wick products into ordinary products and the equation takes the form
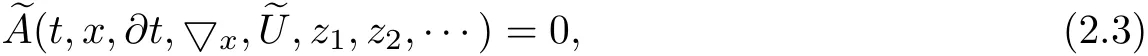

foreachz=(z1,z2,···)∈forsomeq,r,where<r2.
Then,under certain conditions,we can take the inverse Hermite transform U=H-1(u)∈(S)-1and thereby obtain a solution U of the original(Wick)equation(2.2).We have the following theorem,which was proved by Holden et al[10].
Theorem 2.1Suppose u(t,x,z)is a solution(in the usual strong,pointwise sense)of the equation(2.4)for(t,x)in some bounded open set G⊂R×Rdand for all z∈KRq,for some q,R.Moreover,suppose that u(t,x,z)and all its partial derivatives,which are involved in(2.4)are(uniformly)bounded for(t,x,z)∈G×KRq,continuous with respect to(t,x)∈G for each z∈KRqand analytic with respect to z∈KRq,for all(t,x)∈G.
Then there exists U(t,x)∈(S)-1such that u(t,x,z)=(HU(t,x))(z)=(eU(t,x))(z)for all(t,x,z)∈G×KRqand U(t,x)solves(in the strong sense in(S)-1)the equation(2.1)in(S)-1.
§3.Description of Tanh Method
Consider the wick-type SPDE(2.2)
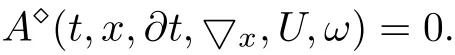
Step 1By the Hermite transform,we transform(2.2)into an ordinary equation(2.3). Considering the transformation˜U(t,x,z)=u(t,x,z)=u(ξ),we reduce the equation(2.3)into

Step 2We suppose that equation(3.1)has the following forms of solution

where ai=ai(x2,x3,···,xd,z,t),i=0,1,···,M,ξ=ξ(x1,x2,···,xd,z,t)are functions to be determined and ψ(ξ)satisfies

so we can easily know that(3.3)has the following solutions
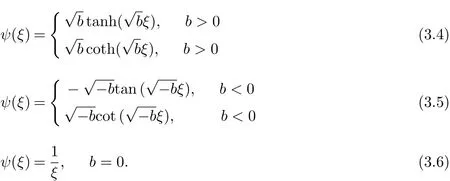
Step 3Substituting(3.2)and(3.3)into(3.1)and then setting the coefficients of xkψi(ξ)of the resulting equation to zero,we can obtain an over-determined system of algebraic equations with respect to a1,···,aM,ξ.Then we solve the above system and get the specific forms of these unknown parameters.
Step 4Substituting the result of Step 3 into(3.2)along with(3.4)~(3.6),we can get the exact solutions u(t,x,z)of(3.1).
Step 5Taking the inverse Hermite transformation of u(t,x,z)obtained in Step 4,i.e.,U(t,x)=H-1(u(t,x,z)),we get the solutions of the wick-type stochastic equation(2.2).
§4.Solutions of Qeneralized Stochastic KdV-Burgers Equation
In this section,we will give exact solutions of(1.1).Taking the Hermite transform of(1.1),we can get the equation

where U depend on t,x and z,eHi,i=1,2,3,4 depend on t and z,z=(z1,z2,···)∈(CN)is a vector parameter.
For the sake of simplicity,we denote u(t,x,z)=eU(t,x,z),Hi(t,z)=eHi(t,z),i=1,2,3,4,so(4.1)becomes
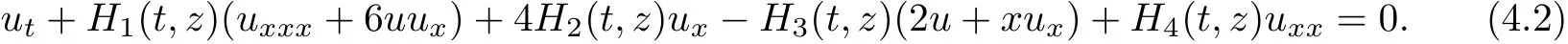
Now let us use the Tanh function method and look for solutions as
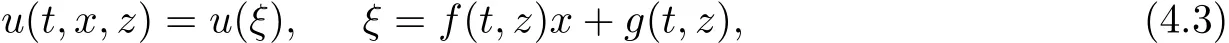
where f(t,z),g(t,z)are functions to be determined later.
We consider that the solutions of the equation(4.2)can be expressed in the form

where ai(t,z)are functions to be determined later.M is a positive integer that can be determined by balancing the differential term of highest order with the nonlinear term in(4.2).ψ(ξ)satisfies the equation(3.3).Then,balancing the linear term of highest order with the nonlinear term in the equation(4.2)leads to set
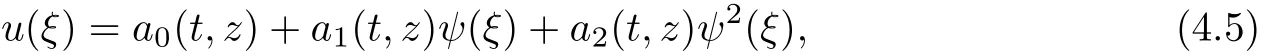
substituting(3.3)and(4.5)into(4.2)and setting the coefficients of xkψi(ξ)to zero,the following system of equations arises

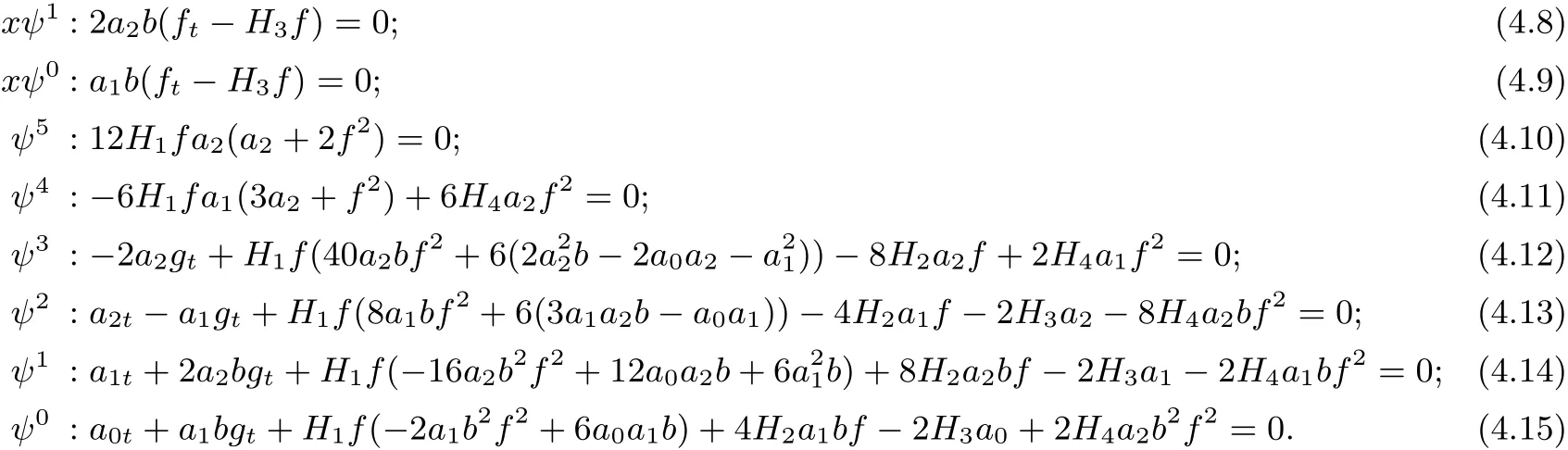
From(4.6)~(4.10),we can obtain

substituting(4.16)and(4.17)into(4.11),we have

According(4.13)and(4.15),we get

When H24(t,z)=100bH21exp(2RtH3(s,z)ds),(4.16)~(4.20)naturally satisfy(4.12)and(4.14). Therefore we get the solution of equation(4.2)as follows

where
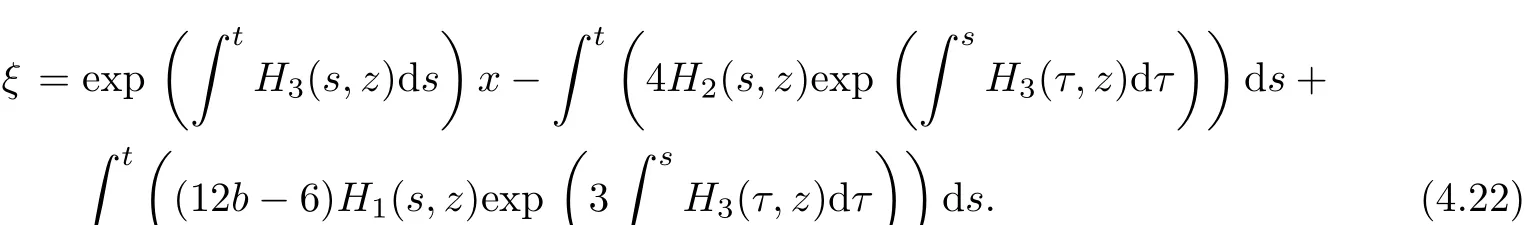
Suppose that h(t)is an integrable function on R+and
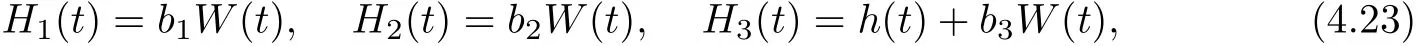
we have
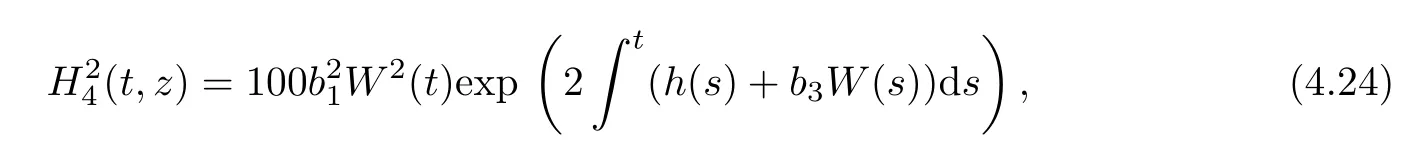
where bi,i=1,2,3 are arbitrary constant,W(t)is Gauss white noise and B(t)is Brownian motion.We know W(t)=˙B(t).
Considering the Hermite transformation of(4.23)and(4.24),we have

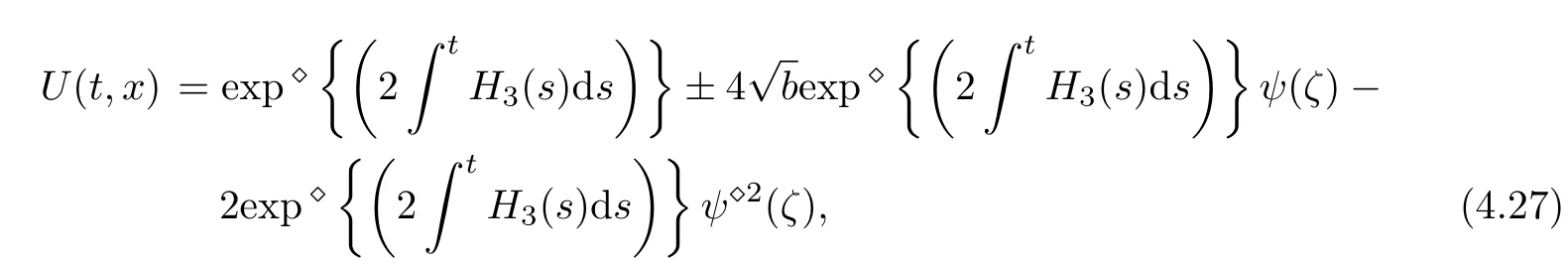
where

According to Theorem 1 and expƒ,we obtain the generalized stochastic solution
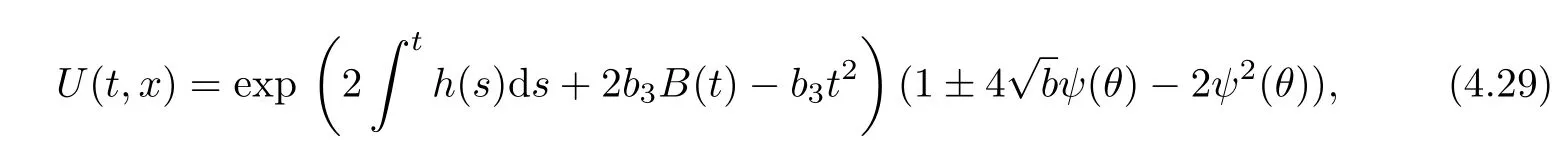
where
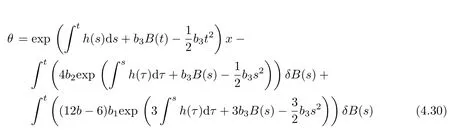
andR(·)δB(t)is the Skorohod integral.
Substituting(3.4)~(3.6)into(4.29)and(4.30),we can get three types of the exact solutions.
(1)The functional solutions of hyperbolic-exponential type(b>0)
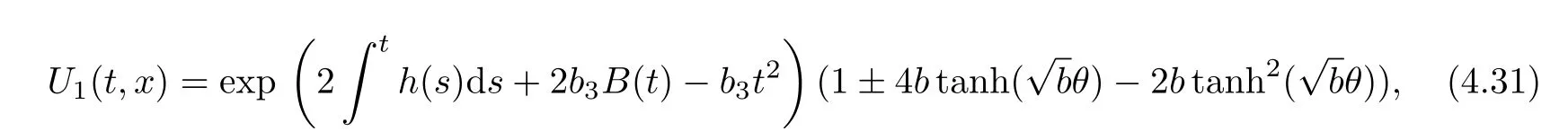
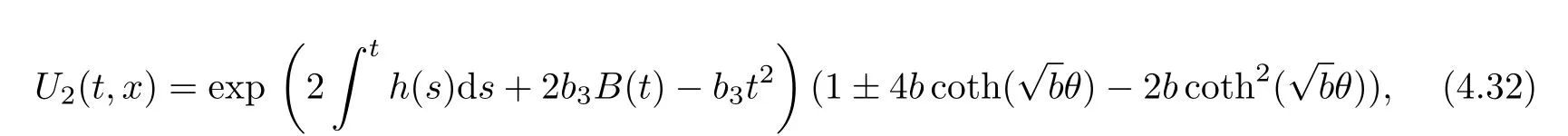
where
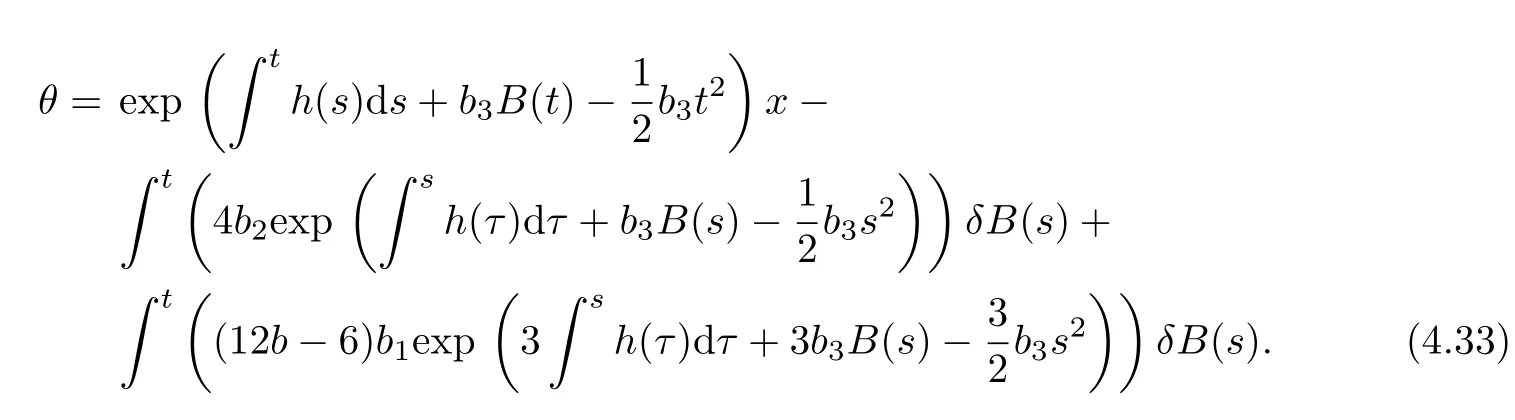
(2)The functional solutions of trigonometric-exponential type(b<0)
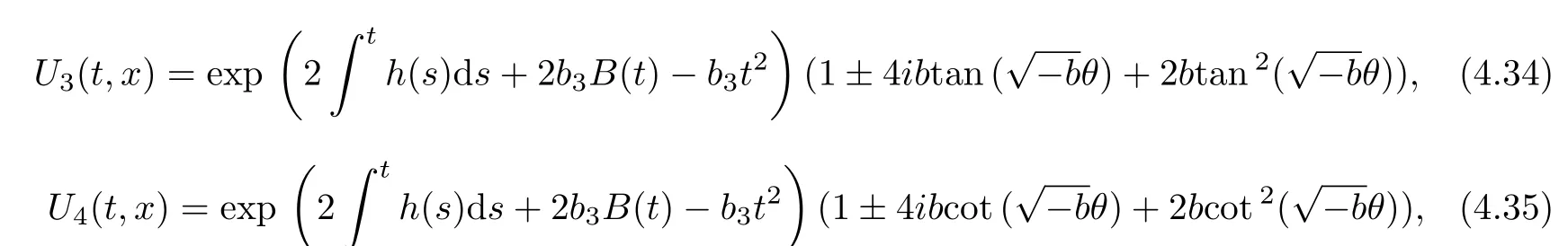
where
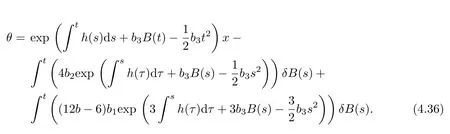
(3)The functional solution of exponential type(b=0)
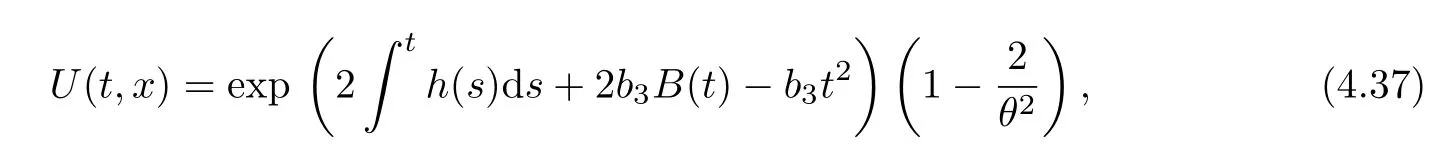
where

§5.Conclusion
We successfully discussed the solutions of the nonlinear stochastic equation with Gaussian white noise.Three types of the exact solutions are obtained which include hyperbolicexponential,trigonometric-exponential exponential function solutions.
[References]
[1]WADATI M.Stochastic Korteweg-de Vries equation[J].Journal of the Physical Society of Japan,1983,52(8):2642-2648.
[2]WADATI M,AKUTSU Y.Stochastic Korteweg-de Vries equation with and without damping[J].Journal of the Physical Society of Japan,1984,53(10):3342-3350.
[3]WADATI M.Deformation of solitons in random media[J].Journal of the Physical Society of Japan,1990,59(12):4201-4203.
[4]BOUARD A de,DEBUSSCHE A.On the stochastic Kortenweg-de Vries equation[J].Journal of Functional Analysis,1998,154(1):215-251.
[5]BOUARD A de,DEBUSSCHE A.White noise driven Korteweg-de Vries equation[J].Journal of Functional Analysis,1999,169(2):532-558.
[6]BOUARD A de,PRINTEMS J.Numerical simulation of the stochastic Korteweg-de Vries equation[J]. Physica D,1999,134:200-226.
[7]BOUARD A de,PRINTEMS J.Effect of a localized random forcing term on the Korteweg-de Vries equation[J].Journal of Computational Analysis and Applications,2001,3(3):183-206.
[8]KONOTOP V V,V´ZQUEZ L.Nonlinear Random Waves[M].Singapore:World Scientific,1994.
[9]PRINTEMS J.The stochastic Korteweg-de Vries equationin L(R2)[J].Journal of Differential Equations,1999,153(2):338-373.
[10]HOLDEN H,OKSENDAL U B.Stochastic Partial Differential Equations:a Modeling,White Noise Functional Approach[M].Boston:Birhkauser,1996.
[11]XIE Ying-chao.Exact solutions for stochastic KdV equations[J].Physics Letters A,2003,310(2-3):161-167.
[12]XIE Ying-chao.Exact solutions for stochastic mKdV equations[J].Chaos Solitons and Fractals,2004,19(3):509-513.
[13]XIE Ying-chao.Exact solutions of the Wick-type stochastic Kadomtsev-Petviashvili equations[J].Chaos Solitons and Fractals,2004,21(2):473-480.
[14]XIE Ying-chao.Exact solutions of the Wick-type stochastic 2-dimensional KdV equations with dissipation[J].Physics Letters A,2005,340(5-6):403-410.
[15]CHENBin,XIEYingchao.WhitenoisefunctionalsolutionsofWick-typestochasticgeneralizedHirotaSatsuma coupledKdVequations[J].Journal of Computational and Applied Mathematics,2006,197(2):345-354.
[16]CHEN Bin,XIE Ying-chao.Periodic-like solutions of variable coefficient and Wick-type stochastic NLS equations[J].Journal of Computational and Applied Mathematics,2007,203(1):249-263.
[17]LIU Qing,ZHU Jia-min,WU Hong-yu.The elliptic equation mapping and its application to stochastic Korteweg-de Vries equation[J].Journal of the Physical Society of Japan,2006,75(1):014002(1-6).
[18]LIU Qing.Various types of exact solutions for stochastic mKdV equation via a modified mapping method[J]. Europhysics Letters,2006,74(3):377-383.
[19]LIU Qing.Some exact solutions for stochastic mKdV equation[J].Chaos Solitons and Fractals,2007,32(3):1224-1230.
[20]LIU Qing.A modified Jacobi elliptic function expansion method and its application to Wick-type stochastic KdV equation[J].Chaos Solitons and Fractals,2007,32(3):1215-1223.
[21]LIU Qing,JIA Dong-li,WANG Zi-hua.Three types of exact solutions to Wick-type generalized stochastic Korteweg-de Vries equation[J].Chaos Solitons and Fractals,2010,215(10):3495-3500.
[22]KIM H,SAKTHIVEL R.Exact solutions of wick-type stochastic equations with variable coefficients[J]. Reports on Mathematical Physics,2011,67(3):415-429.
O175.2Document code:A
date:2014-04-03
Supported by the National Natural Science Foundation of China(11271008,61072147)
Biographies:LIU Shao-qing(1977-),female,native of Qingdao,Shandong,a lecturer of Shandong University of Science and Technology,Ph.D.,engages in soliton and integrable system;GAO Guo-cheng(1963-),male,native of Xinyang,Henan,a professor of Shandong University of Science and Technology,M.S.D.,engages in control theory and optimization.
杂志排行
Chinese Quarterly Journal of Mathematics的其它文章
- Distance Integral Complete Multipartite Graphs with s=5,6
- Cyclic Codes with Complementary Duals over Fp+vFp
- Uniform Blow-up Behavior for Degenerate and Singular Parabolic Equations
- Vertex-distinguishing IE-total Colorings of Complete Bipartite Graphs K8,n
- Common Fixed Point Theorems in Non-normal Cone Metric Spaces with Banach Algebras
- LrConvergence for Arrays of Rowwise Negatively Superadditive Dependent Random Variables
