Cyclic Codes with Complementary Duals over Fp+vFp
2016-09-15ZHANGGuanghuiLIUQingqing
ZHANG Guang-hui,LIU Qing-qing
(School of Mathematical Sciences,Luoyang Normal University,Luoyang 471022,China)
Cyclic Codes with Complementary Duals over Fp+vFp
ZHANG Guang-hui1,LIU Qing-qing2
(School of Mathematical Sciences,Luoyang Normal University,Luoyang 471022,China)
In this paper,we characterize the necessary and sufficient conditions for a cyclic code of length n over Fp+vFpto be an LCD code,where p is an odd prime.
cyclic codes;LCD codes
2000 MR Subject Classification:33D05,33C60,34A25
Article ID:1002—0462(2016)02—0118—07
Chin.Quart.J.of Math.
2016,31(2):118—124
§1.Introduction
Codes over finite rings have been studied in the early 1970s and were initiated by Blake[12]. In the 1990s Hammons et al[6]discovered that certain good nonlinear binary codes could be found as images of linear codes over Z4under the Gray map.Therefore since then codes over finite rings have received much attention and have been studied by many authors[3,5,7].
However,these studies are concentrated on the situation in which the ground rings associated with codes are finite chain rings in general.In such cases,linear codes over certain finite rings have been characterized in[5,8,12].The case when the ground ring is not a finite chain ring seems to be more difficult.More recently,linear codes over the ring Fp+vFp,where v2=v and p is a prime,which is not a chain ring but a semi-local ring have been considered.In[17]Zhu et al gave some results about cyclic codes over F2+vF2,where it is shown that cyclic codes over the ring are principally generated;in[16]Zhu et al studied(1-2v)-constacyclic codesover Fp+vFp,where p is an odd prime.They determined the image of a(1-2v)-constacyclic code over Fp+vFpunder the Gray map and the generator polynomials of such constacyclic codes over Fp+vFpand proved that constacyclic codes over the ring are principally generated. In[15]we characterized the polynomial generators of all constacyclic codes over Fp+vFpand their dual codes,where p is an odd prime.
A linear code with a complementary dual(an LCD code)was defined in[9]to be a linear code C whose dual code C⊥satisfies C∩C⊥=0,where it was shown that asymptotically good LCD codes exist and that LCD codes have certain other attractive properties.In the later[14],Yang and Messey showed the necessary and sufficient condition for a cyclic code C of length n to be an LCD code is that the generator polynomial g(x)of C be self-reciprocal and all the monic irreducible factors of g(x)have the same multiplicity in g(x)as in xn-1.
In this paper,by virtue of the decomposition of cyclic codes over Fp+vFpwe describe that the necessary and sufficient condition of cyclic codes over the rings to be an LCD code.
§2.Preliminaries
Let Fpbe a finite field with p elements,where p is an odd prime.Throughout this paper,let R be the commutative ring Fp+vFp={a+vb|a,b∈Fp},where v2=v.The ring R is a semilocal ring with two maximal ideals given by〈v〉={av|a∈Fp}and〈1-v〉={a(1-v)|a∈Fp}. It is easy to verify that both R/〈v〉and R/〈1-v〉are isomorphic to Fp.A linear code C of length n over R is an R-submodule of Rn.For x=(x1,x2,···,xn),y=(y1,y2,···,yn)∈Rn,we define the inner product of x,y by

and define the orthogonal code of C by

which is called the dual code of C.Then C⊥is a linear code over R.In[13],it was proved that for any linear code C over a finite Frobenius ringeR,|C||C⊥|=|eR|n.
A linear code C of length n over R is cyclic if the code is invariant under the shift operator(c0,c1,···,cn-1)7→(cn-1,c0,···,cn-2).Cyclic codes of length n over R can be identified as ideals in the quotient ring R[x]/〈xn-1〉via the isomorphism from Rnto R[x]/〈xn-1〉defined by c=(c0,c1,···,cn-1)7→c(x)=c0+c1x+···+cn-1xn-1.Then C is identified with the set of all polynomial representations of its codewords.Every cyclic code C of length n over Fpis a principal ideal in Fp[x]/〈xn-1〉.Then there is a unique monic polynomial g(x)of minimum degree in C.This polynomial generates C and divides xn-1.This polynomial g(x)is called the generator polynomial for C.It will be convenient to adopt the notation C=〈g(x)〉to denote the fact that C is the ideal generated by g(x)and that g(x)is the generator polynomial for C.
We know that the ring R has two maximal ideals〈v〉and〈1-v〉.Their residue fields are both Fp.Note that any element c of Rncan be expressed as c=va+(1-v)b,where a,b∈Fnp.Thus we have two canonical projections defined as follows
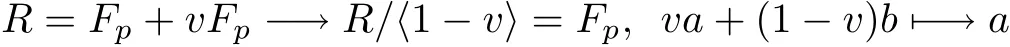
and

We simple denote these two projections by“σ”and“τ”,respectively.Denote by rσand rτthe images of an element r∈R under these two projections,respectively.These two projections can be extended naturally from R[x]to Fp[x].
For k>0,Ikdenotes the k×k identity matrix.Any nonzero linear code C over R is permutation-equivalent to a code generated by the following matrix

where Aiand Bjare matrices with entries in Fpfor i,j=1,2,3,4.Such a code C is said to have type p2k1pk2pk3and|C|=p2k1+k2+k3in[11,16].For later convenience the above generator matrix can be written in the form
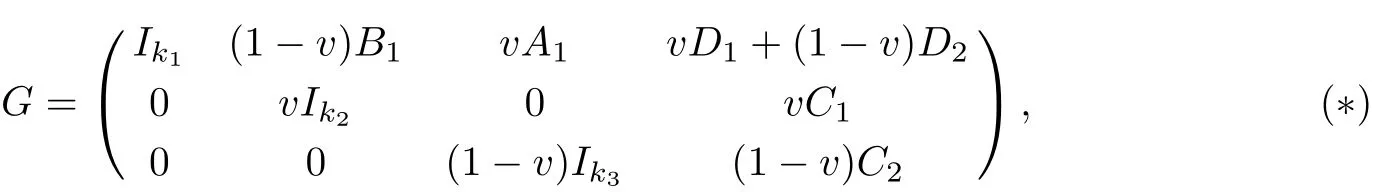
where D1=(A2,A3),D2=(B2,B3),C1=(A4,0),C2=(0,B4).
Let C be a linear code of length n over R with generator matrix in form(∗).Define and


Obviously,C1and C2are linear codes over Fp.
The code C1is permutation-equivalent to a code with generator matrix of the form

where Biare p-ary matrices for i∈{1,2,3,4}.And the code C2is permutation-equivalent to a code with generator matrix of the form

where Aiare p-ary matrices for i∈{1,2,3,4}.It is easy to see that dim C1=k1+k3,dim C2= k1+k2.
For a code C of length n over R,let a∈R.The submodule quotient is a linear code of length n over R,defined as follows

The codes(C:v)σand(C:(1-v))τover the field Fpis called the torsion codes associated with the code C over the ring R.
§3.Decomposition of Linear Codes over Fp+vFp
Lemma 1With notations as above.Let C be a linear code of length n over R.Then(1)C1=(C:(1-v))τ;(2)C2=(C:v)σ.
Proof(1)Let x=va+(1-v)b and x∈(C:(1-v)).From(1-v)x∈C,we have that

which leads to b∈C1,i.e.,xτ∈C1.Therefore we obtain that(C:(1-v))τ⊆C1.
If b is an element of C1,then we have that va+(1-v)b∈C for some a∈Fnp.Let x=va+(1-v)b.Since(1-v)x∈C,which shows that x∈(C:(1-v)).Hence b=xτ∈(C:(1-v))τ,then(C:(1-v))τ⊇C1.Therefore(C:(1-v))τ=C1,as required.
(2)Let y=va+(1-v)b and y∈(C:v).Since vy∈C,we have va=vy∈C,which implies that a∈C2.Therefore yσ=a∈C2.It follows that(C:v)σ⊆C2.
Let a∈C2.Then we have that va+(1-v)b∈C for some b∈Fnp.Let y=va+(1-v)b. Since vy∈C,which shows that y∈(C:v).Hence a=yσ∈(C:v)σ,then(C:v)σ⊇C2. Therefore we get the desired result.
In the following,ATdenotes the transpose of the matrix A.
Theorem 2Let C be a linear code of length n over R with generator matrix in form(∗).Then
(1)

where E1=(-A2,B4A1-A3)T,E2=(A4B1-B2,-B3)T,P=(-A4,0)T,Q=(0,-B4)T;k=k1+k2+k3,is a generator matrix for C⊥and a parity check matrix for C.
(2)((C:v)σ)⊥=(C⊥:v)σ;((C:(1-v))τ)⊥=(C⊥:(1-v))τ.
Proof(1)It is straightforward to check that HGT=0.Let D be the R-submodule generated by H,then D⊆C⊥.Since R is a Frobenius ring,we have that|C||C⊥|=|R|n.It follows that
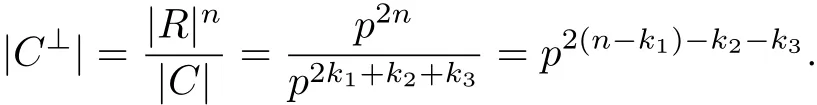
Note that|D|=p2(n-k)+k3+k2=p2(n-k1)-k2-k3and we obtain that|D|=|C⊥|,hence D=C⊥.
(2)We first prove that(C⊥:v)σ⊆((C:v)σ)⊥.Let x∈(C⊥:v)and y∈(C:v). Then vx∈C⊥and vy∈C,so(vx)(vy)T=0,i.e.,v(xyT)=0.Hence xyT∈(1-v)R and(xσ)(yσ)T=0,which implies that(C⊥:v)σ⊆((C:v)σ)⊥.On the other hand,by Lemma 1 and Theorem 2(1),we have that

Hence dim(C⊥:v)σ=dim((C:v)σ)⊥,which follows that((C:v)σ)⊥=(C⊥:v)σ.
The proof of the second equality is similar to that of the first one and is left to the reader.
Let A,B be the codes over R.We denote that A⊕B={a+b|a∈A,b∈B}.
Theorem 3With the above notations,let C be a linear code of length n over R.Then C can be uniquely expressed as C=vC2⊕(1-v)C1.Moreover,we also have C⊥=vC⊥2⊕(1-v)C⊥1.
ProofWe first prove the uniqueness of the expression of every element in vC2⊕(1-v)C1. Let va2+(1-v)a1=vb2+(1-v)b1,where a2,b2∈C2;a1,b1∈C1.Then v(a2-b2)=(1-v)(b1-a1),which implies that a1=b1and a2=b2.Hence|vC2⊕(1-v)C1|=|C1||C2|=
pk1+k3pk1+k2=p2k1+k2+k3=|C|.
Next we prove that vC2⊕(1-v)C1⊆C.Let a∈(C:v)and b∈(C:(1-v)).Then va∈C;(1-v)b∈C.Setting a=va1+(1-v)a2,b=vb1+(1-v)b2,where a1,a2,b1,b2∈Fnp. Then aσ=a1∈C2,bτ=b2∈C1.Thus vaσ+(1-v)bτ=va1+(1-v)b2=va+(1-v)b∈C. Hence vC2⊕(1-v)C1⊆C.Note that|vC2⊕(1-v)C1|=|C|,therefore C=vC2⊕(1-v)C1.
Finally,we prove the second statement.By the first statement,Theorem 2(2)and Lemma 1,we have that

which is the desired result.
§4.Cyclic Codes with Complementary Duals over Fp+vFp
Similar to the linear code over finite field with a complementary dual(an LCD code),we may define the LCD code over R,which is defined to be a linear code C over R whose dual code C⊥satisfies C∩C⊥=0.In the following,we characterize the condition for a cyclic code to be an LCD code.
Theorem 4With the above notations,let C=vC2⊕(1-v)C1be a linear code of length n over R.Then C is an LCD code if and only if C1and C2are both LCD codes.
Proof(=⇒)Suppose that C1∩C⊥1/=0,then there exists 0/=x∈C1∩C⊥1.Since x∈C1and C=vC2⊕(1-v)C1,we have(1-v)x∈C;Since x∈C⊥1and C⊥=vC⊥2⊕(1-v)C⊥1,we have(1-v)x∈C⊥.So(1-v)x∈C∩C⊥.Noting that(1-v)x/=0,we get a contradiction. Hence we obtain C1is an LCD code.Similarly,C2is also an LCD code.
(⇐=)Let c be an arbitrary element in C∩C⊥.By Theorem 3,C=vC2⊕(1-v)C1,C⊥= vC⊥2⊕(1-v)C⊥1,thus we can assume that c=va2+(1-v)a1,a1∈C1,a2∈C2and c= vb2+(1-v)b1,b1∈C⊥1,b2∈C⊥2,which imply that a1=b1∈C1∩C⊥1and a2=b2∈C2∩C⊥2. So a2=b2=0,a1=b1=0.Hence c=0.Therefore C is an LCD code.
Lemma 5With the above notations,let C=vC2⊕(1-v)C1be a linear code of length n over R.Then C is a cyclic code if and only if C1and C2are both cyclic codes.
Proof(=⇒)Note that C be a cyclic code of length n over R,i.e.,C is an ideal in the ring R[x]/〈xn-1〉Then(C:v)and(C:(1-v))are two ideals in the ring R[x]/〈xn-1〉,i.e.,two cyclic codes.Henceand C1=are two ideals in the ring Fp[x]/〈xn-1〉,i.e.,both cyclic.
(⇐=)Let C1and C2be two cyclic codes and π be the shift operator.For arbitrary element c∈C,since C=vC2⊕(1-v)C1,we may suppose that c=vc2+(1-v)c1,c1∈C1,c2∈C2. Then π(c)=π(vc2+(1-v)c1)=vπ(c2)+(1-v)π(c1)∈vC2⊕(1-v)C1=C.Hence C is a cyclic code.
Suppose that f(x)is a monic(i.e.,leading coefficient 1)polynomial of degree d with f(0)= c/=0.Then by the monic reciprocal polynomial of f(x)we mean the polynomial f∗(x)= c-1xdf(x-1).
Lemma 6[14,Theorem]If g(x)is the generator polynomial of a cyclic code C of length n,then C is an LCD code if and only if g(x)is self-reciprocal(i.e.,g∗(x)=g(x))and all the monic irreducible factors of g(x)have the same multiplicity in g(x)and in xn-1.
Theorem 7Let C be a cyclic code over R and let g1(x),g2(x)be generator polynomials for C1and C2,respectively.Then C is an LCD code if and only if g1(x),g2(x)are self-reciprocal and all the monic irreducible factors of every gi(x)have the same multiplicity in gi(x)and in xn-1 for i=1,2.
ProofIt follows immediately from Theorem 4 and lemmas 5 and 6.
A reversible code is a code such that reversing the order of the components of a codeword gives always again a codeword.It was shown in[10]that a cyclic code is reversible if and only if its generator polynomial is self-reciprocal,which immediately establishes the following corollary that covers the cyclic codes of greatest interest,namely those whose generator polynomials have no repeated factors,cf[4].
Lemma 8A q-ary cyclic code,whose length n is relatively prime to the characteristic p of Fq,is an LCD code if and only if it is a reversible code.
Thus we readily obtain the following result.
Theorem 9Let C=vC2⊕(1-v)C1be a cyclic code over R whose length n is relativelyprime to p and let g1(x),g2(x)be generator polynomials for C1and C2,respectively.Then C is an LCD code if and only if C1and C2are both reversible codes if and only if g1(x),g2(x)are self-reciprocal.
[References]
[1]BLAKE I F.Codes over certain rings[J].Inform Control,1972,20:396-404.
[2]BLAKE I F.Codes over integer residue rings[J].Inform Control,1975,29:295-300.
[3]CALDERBANK A R,SLOANE N J A.Modular and p-adic cyclic codes[J].Des Codes Cryptogr,1995,6:21-35.
[4]CASTAGNOLI G,MASSEY J L,SCHOELLER P A,et al.On repeated-root cyclic codes[J].IEEE Trans Inform Theory,1991,37:337-342.
[5]GULLIVER T A,HARADA M.Codes over F3+uF3and improvements to the bounds on ternary linear codes[J].Des Codes Cryptogr,2001,22:89-96.
[6]HAMMONS A R JR,KUMAR P V,CALDERBANK A R,et al.The Z4linearity of Kerdock,Preparata,Goethals and related codes[J].IEEE Trans Inform Theory,1994,40(2):301-319.
[7]KANWAR P,L´OPEZ-PERMOUTH S R.Cyclic codes over the integers modulo pm[J].Finite Fields Appl,1997,3:334-352.
[8]LING San,BLACKFORD J.Zpk+1-linear codes[J].IEEE Trans Inform Theory,2002,48:2592-2605.
[9]MASSEY J L.Linear codes with complementary duals[J].Discrete Math,1992,106/107:337-342.
[10]MASSEY J L.Reversible codes[J].Inform and Control,1964,7:369-380.
[11]WAN Zhe-xian.Quaternary Codes[M].Singapore:World Scientific,1997.
[12]WOLFMANN J.Binary image of cyclic codes over Z4[J].IEEE Trans Inform Theory,2001,47(5):1773-1779.
[13]WOOD J.Duality for modules over finite rings and applications to coding theory[J].Amer J Math,1999,121:555-575.
[14]YANG Xiang,MASSEY J L.The condition for a cyclic code to have a complementary dual[J].Discrete Math,1994,126:391-393.
[15]ZHANG Guang-hui,CHEN Bo-cong.Constacyclic codes over Fp+vFp[J].http://arxiv.org/pdf/1301.0669.pdf,2012.
[16]ZHU Shi-xing,WANG Li-qi.A class of constacyclic codes over Fp+vFpand its gray image[J].Discrete Math,2011,311:2677-2682.
[17]ZHU Shi-xin,WANG Yu,SHI Min-jia.Some results on cyclic codes over F2+vF2[J].IEEE Trans Inform Theory,2010,56(4):1680-1684.
O157.4Document code:A
date:2014-02-21
Supported by the Science and Technology Development Program of Henan Province in 2016(162102410052);Supported by the Natural Science Foundation from the Educational Department of Henan Province(14B110004,2013-JSJYYB-063)
Biographies:ZHANG Guang-hui(1973-),male,native of Yexian,Henan,an associate professor of Luoyang Normal University,Ph.D.,engages in classical error-correcting codes,codes over rings and quantum errorcorrecting codes;LIU Qing-qing(1978-),female,native of Luoyang,Henan,an associate professor of Luoyang Normal University,M.S.D.,engages in applications of computer and software.
杂志排行
Chinese Quarterly Journal of Mathematics的其它文章
- Distance Integral Complete Multipartite Graphs with s=5,6
- Uniform Blow-up Behavior for Degenerate and Singular Parabolic Equations
- Exact Solutions of the Wick-type KdV-Burgers Equation
- Vertex-distinguishing IE-total Colorings of Complete Bipartite Graphs K8,n
- Common Fixed Point Theorems in Non-normal Cone Metric Spaces with Banach Algebras
- LrConvergence for Arrays of Rowwise Negatively Superadditive Dependent Random Variables
