织物单向悬垂性特征参数的提取

梅再欢，沈　伟，王　妍，周　华

(浙江理工大学先进纺织材料与制备技术教育部重点实验室，杭州310018)



织物单向悬垂性特征参数的提取

梅再欢，沈伟，王妍，周华

(浙江理工大学先进纺织材料与制备技术教育部重点实验室，杭州310018)

为了改进传统悬垂性的测量方法，客观反映织物的悬垂性，利用微软的Kinect传感器提出了一种单向悬垂性三维测量方法。通过Kinect传感器获取织物试样的三维悬垂模型并保存为STL(立体光造型)格式文件，通过删除杂质、裁剪、矫正图像得到织物试样的三维悬垂投影，水平截取悬垂投影图像，求出水平面与试样轮廓的交线，将这些交线整理成头尾相连的一条直线段并滤波得到二维悬垂投影曲线，通过相关算法识别出该投影曲线的波峰、波谷点，提取了表征单向悬垂程度指标(单向悬垂系数)和悬垂形态指标(峰数、峰对称性系数等)，建立了单向悬垂性评价体系，并通过实验与标准测试悬垂性的方法以及人为主观评价方法做了相关性分析，结果发现单向悬垂指标在描述织物悬垂性上与传统方法和主观评价法均一致，实现了织物悬垂性的三维测量。

织物；悬垂性；悬垂指标；Kinect；三维测量；图像处理

0　引　言

织物的悬垂性是织物仅在自身重力作用下产生三维形变的特征[1]，所谓单向悬垂性是指织物受力方向为平行于织物平面的悬垂性，大部分织物如服装、窗帘等的悬垂性都属于这种情况。传统悬垂性的测试方法大都基于伞式投影法[2]，即从圆形试样的投影轮廓中提取悬垂指标。这种方法织物受垂直于其平面的重力作用，与织物实际受力状态不符，不能客观反映织物的悬垂特性，而且存在着试样透光、试样面积过小等局限性。而单向悬垂性非常接近织物的实际悬垂特性，有必要研究单向悬垂性测量方法来评价织物的悬垂性。单向悬垂性是织物在自然悬挂状态下的三维视觉特征，其测量方法应该对自然悬挂试样进行三维测量[3]，即获取试样的三维模型，从三维模型中提取悬垂特征指标。这种测量方法的一个关键就是如何获取试样的三维模型，实现三维测量。悬垂性三维测量技术已有很多研究[4-6]，但是不能直观获取织物的三维模型，而且都是在伞式法的基础上加以改进。现有的三维扫描仪虽然能够建立织物的三维模型，但是一般价格昂贵、操作复杂而且扫描条件苛刻，不适宜测试织物的悬垂性。

本文利用微软的Kinect传感器上提出了单向悬垂性的一种三维测量方法。Kinect不仅价格低廉，而且能快速方便地获取试样的三维悬垂模型。其原理是试样以一定的夹持方式自然悬挂，利用Kinect从多个角度重复扫描，捕获试样的深度图像，将多幅深度图像进行点云拼接[7]，并融合在一个坐标系下得到了试样的三维模型，结合图像处理技术提取悬垂指标。单向悬垂性非常接近织物实际悬挂状态下的受力特征，更加符合实际悬垂性的测量，更能客观反映织物三维悬垂特性，避免了传统测试法的一些弊端。

1　织物三维模型的获取

Kinect是Microsoft公司推出的一款3D体感摄像机，主要由PS1080 SoC图像处理器芯片、红外发射器、彩色摄像头、红外摄像头等部件组成，红外发射器和红外摄像头用来获取物体的深度图像，彩色摄像头用于采集视角范围内的彩色视频图像。

Kinect获取试样的三维模型是将多幅深度图像利用微软研究院推出的KinectFusion[8-9]技术进行点云拼接得到的。Kinect获取深度图采用了Light Coding技术[10]，即用激光散斑给需要测量的空间编码，激光散斑具有高度的随机性，距离不同，散斑图案也不同，因此可以通过散斑图案变化就可获取物体的空间信息。通过深度数据可以获得物体表面每个点的三维坐标，以此形成一个点的集合，即“点云”。借助KinectFusion三维重建算法，Kinect能以每秒超过百万个点的速度[11]对点云进行拼接，将多幅深度图像合成在一个坐标系下，就建立三维实体模型，如图1。通过对规则物体进行扫描，计算其模型尺寸并与实际尺寸对比，本测试装置的精度在1～3 mm之间，相对误差在0.2 %左右，符合测试要求。

图1　织物悬垂三维模型

2　单向悬垂性特征参数的提取

利用Kinect对单向悬垂性进行三维测量首先需要建立试样的三维模型，然后用一水平面截取试样底部得到水平投影曲线，识别出此曲线的波峰、波谷点，进而计算出单向悬垂系数、弯曲指数、峰高等单向悬垂指标。之所以从底部的轮廓中提取悬垂特征指标，是因为越靠近试样的底部，织物悬垂受刚性夹持的影响越小，越能反映织物在自然状态下的悬垂性。

2.1单向悬垂投影曲线的提取

所谓单向悬垂投影曲线是指试样三维模型底部与水平面的交线。Kinect传感器扫描出来的深度图像包含了织物表面每点的三维坐标，并且是以STL格式文件存储的。STL是用许多离散的三角形小平面逼近原三维实体的数据模型。每一个三角

面片由四个数据项表示，即三角形三个顶点的坐标和该三角平面的外法线矢量，三个顶点的排序遵循右手定则。要得到悬垂投影曲线，实际上就是求每个三角面片的三条边与截平面的交线的集合，将这些交线整理成头尾相连的线段并滤波，便得到投影曲线。

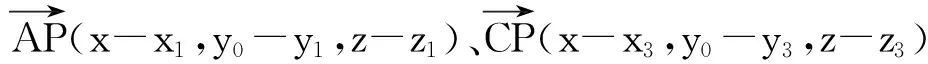
(1)

则可以解得：

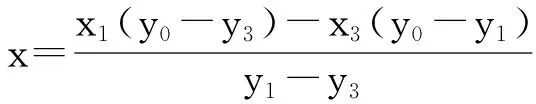
由此求得了平面ABC与平面y=y0在线段AC上的交点P的坐标。

图2　水平面截三角平面示意图

同理可以求得平面y=y0与线段AB或BC上的交点。连接两交点便得到平面y=y0与平面ABC的交线。读取STL格式文件，可以得到三角面片的个数，按照以上方法可以得到平面y=y0与每个三角面片的交线的集合。这些线段都是离散的，需要将其整理成头尾相连的一条直线段。由于三角平面数量大，交点密集，直线段也便近似为一条曲线，对这条曲线进行滤波，消除噪声，便得到图3所示光滑的单向悬垂投影曲线。

图3　单向悬垂投影曲线

2.2波峰、波谷点的获取

获取单向悬垂性的各个指标，必须找到此投影曲线的一些关键点即波峰和波谷点，如图3中的点。

识别波峰和波谷点也就是求投影曲线的极大值和极小值点，可以通过求导数判断。假设投影曲线上有N个点，其坐标为(xi,yi)，令yi=f(xi)，1≤i≤N。如果连续曲线在某点的导数f′(xi)=0，且f′(xi-1)>0，f′(xi+1)<0，那么(xi,yi)为曲线上的一个极大值点，即波峰点；相反如果f′(xi)=0，f′(xi-1)<0，f′(xi+1)>0，那么(xi,yi)为曲线上的一个极小值点，即波谷点。问题的关键便转为求曲线的每一点的导数。由于曲线上点比较密集，相邻点的间距很小，曲线上某点的导数可以用数值微分中点方法近似计算：

(2)

程序中可以设置一个循环，不断判断f′(xi)、f′(xi-1)、f′(xi+1)的符号，便可以识别出曲线上所有的波峰和波谷点，波数也便确定了。但实际上曲线存在细微的波动，将任意起伏记为波峰或波谷不合理也不合实际。对此可以限定波峰与波谷间的距离d来计数波峰或波谷，如果一个波峰点(ti+1,Ti+1)与其相邻的一个波谷点(bi,Bi)间的距离d≤d0(d0为波峰和波谷间的最小距离)，那么可以认为(ti+1,Ti+1)不为波峰点，同理可以判断某点是否为波谷点。

2.3曲线长度L及其修正系数ξ

曲线长度可用下式近似计算：

(3)

式中：N为曲线上点的个数，(xi,yi)、(xi+1,yi+1)为曲线上点的坐标，N越大越精确。由于L是一个近似值，相对于真实值会存在一定误差，因此需要对L修正，曲线长度修正系数ξ定义为试样宽度L0与L的比值：

(4)

2.4单向悬垂性指标的计算

单向悬垂性指标包括悬垂程度指标：单向悬垂系数，以及悬垂形态指标：峰数、弯曲指数、弯曲变异系数、峰高、峰高变异系数、峰对称性系数及其变异系数。

2.4.1单向悬垂系数F

单向悬垂系数定义为试样宽度与悬垂宽度的差值占试样宽度与折叠宽度的差值的百分比，用公式表示如下：

(5)

其中：L0—试样宽度(mm)；L1—折叠宽度(mm)；L2—悬垂宽度(mm)。织物悬垂示意图如图4所示。

图4　织物悬垂示意图

悬垂系数反映了织物的悬垂程度，其值越大表示试样越柔软，悬垂性越好；值越小表示试样越硬挺，悬垂性越差。

l=xmax-xmin

(6)

w=ymax-ymin

(7)

式中：xmax、xmin分别为曲线上最大横坐标和最小横坐标；ymax、ymin分别为曲线上最大纵坐标和最小纵坐标。则此矩形刚好能包围投影曲线，那么悬垂宽度L2为矩形的长度l，即L2=l。对L2进行修正，悬垂系数最终计算公式如下：

(8)

图5　悬垂宽度

2.4.2峰数

峰数为波峰点的个数，在2.2节识别波峰、波谷点时峰数便已确定。峰数反映了单向悬垂程度，峰数越多，悬垂性越好。

弯曲指数定义为相邻两个波谷之间的曲线长度与其水平距离的比值。弯曲指数反映了悬垂弯曲的程度，其值越大，波的形状越是瘦高，悬垂性越好。

记波谷点的坐标为(bi,Bi)，1≤i≤n，n为波谷数，两波谷间的曲线长度li，则相邻两个波谷间的水平距离di为：

di=bi+1-bi

(9)

式中：n′为两波谷间曲线上点的个数。对di和li用系数ξ修正，则平均弯曲指数为：

(10)

对应的变异系数为：

(11)

峰高定义为一个波峰到相邻两个波谷的平均高度间的距离。峰高反映了悬垂投影曲线的幅值变化，即悬垂折曲的深浅。

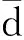
(12)

峰高hi为：

(13)

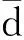
(14)

(15)

3　测试与分析

为了验证按照上述方法提取的悬垂指标是否可以表达悬垂性，需要将本方法测得的数据与标准测试悬垂性的方法所测得的数据对比。

选择20块不同风格的涤纶织物。采用XDP-1型织物悬垂性测试仪，参照依标准GB/T23329-2009《纺织品 织物悬垂性试验方法》测试伞式悬垂性指标。对于单向悬垂性指标的测试，通过大量实验取其试样高度为50cm，宽度为87cm。表1和表2分别为两种方法所测得的数据。

单向悬垂性测试法实验中，试样一端夹持另一端自由悬垂即模拟窗帘的悬挂形式。

表1　伞式悬垂指标

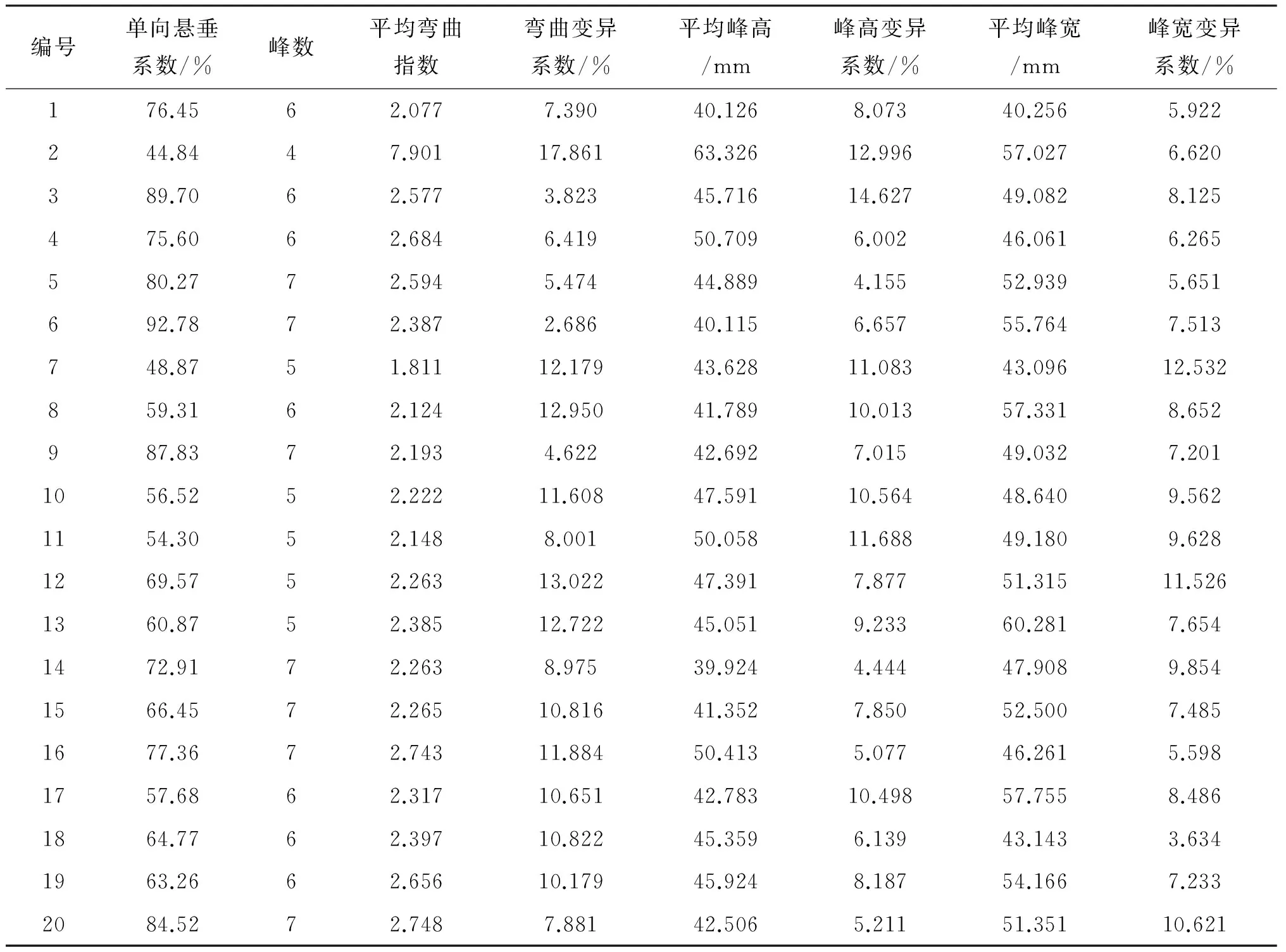
表2　单向悬垂指标测试结果

由于单向法与伞式法的测试原理和评价指标都不同，因此不能直接对测试指标作比较。为此，本文在此引出一表达悬垂性的新的综合性指标“美感系数”：将单向法和伞式法的各评价指标利用SPSS统计软件的主因子分析法得到各指标的权重系数，那么就可以得出一个综合指标，并命名为美感系数，表达悬垂性。式(16)-(17)为两种方法计算得到的美感系数表达式。对两种方法所得到的美感系数进行相关性分析，就可以知道两种方法所测得的美感系数是否一致。表3为单向法和伞式法的美感系数。

(16)

B2=0.553f2+0.243θ2+0.168h2

(17)

式中：B2为单向悬垂美感系数，f2为单向悬垂系数，θ2为弯曲变异指数，h2峰高变异指数。

表3　单向法和伞式法的美感系数

对单向法和伞式法的美感系数作相关性分析，结果见图6。

由图6可知，单向悬垂美感系数与伞式悬垂美感系数的相关系数的平方R2=0.929(R=0.964，置信度为0.01)，且其相关方程为y=0.853x-5.823，说明两者在置信度0.01时是高度线性相关的。因此，单向悬垂测试法与伞式悬垂性测试法在描述织物的悬垂性上是一致的。

图6　两种美感系数的相关性

悬垂性的好差是面料固有特性作用于人的感觉器官而产生的一种心理反应，是人对织物的一种视觉感受。因此，人的主观判断是评价织物悬垂性的最直接的方法。为此本文又将单向悬垂性测试数据与人为主观评价数据作对比，进一步验证单向悬垂指标的可靠性。为保证人为主观评价的准确性，请纺织行业专家和非专业人士各10人，对试样的悬垂程度和悬垂形态的匀称性进行评判并打分(最高分为20，表示悬垂性最优，最低分为1，表示悬垂性最差)。人为主观评分=(专家×60%+非专业人士×40%)/10，算出每块面料的最终评分并排序，并将单向法所测得的美感系数排序，结果见表4。将两种方法的排序结果进行相关性分析，结果见图7。

图7　主观评价法和单向法的相关性

由图7可知，单向法和主观评价法的相关系数的平方R2=0.935(R=0.967，置信度为0.01)，相关方程为y=0.967x+0.347，说明两者在置信度为0.01时是高度线性相关的。因此，单向悬垂性测试指标可以描述织物的悬垂性。

表4　人为主观评价和单向法测试结果排序表

综上所述，本文提取的单向悬垂性指标与标准测试悬垂性的方法和主观评价法所测结果具有一致性，因此可以用来描述织物的悬垂特性。

4　结　论

本文在Kinect扫描仪的基础上提出了一种悬垂性的三维测量方法即单向悬垂性测量法。通过KinectFusion点云拼接技术获取了织物的三维悬垂模型，经图像处理并借助相关算法提取了单向悬垂性各指标，建立了单向悬垂性评价指标体系，并与标准测试悬垂性的方法和主观评价法做了对比分析。结果显示，本方法提取的悬垂指标可以用来描述织物的悬垂性，而且更加符合织物悬的实际受力特征，克服了传统悬垂性测试存在的诸如经纬双向受力、试样透光、测试面积过小等弊端，实现了悬垂性的三维测量，为织物悬垂性的测试提供一种新途径。

[1] AI-GAADI B, GOKTEPE F, HALASZ M. A new method in fabric drapes measurement and analysis of the drape formation process [J]. Textile Research Journal, 2012, 82(5): 502.

[2] 徐军,姚穆.伞式织物动态悬垂测试装置的研制与应用[J].上海纺织科技,1998,26(3):55-56.

[3] 王军,鲍海明,魏仲慧,等.光学三维轮廓测量技术综述[J].光机电信息,2005,(2):32-36.

[4] 沈毅,周华,尹红媛.ZYF-3型织物悬垂三维测试仪的研制[J].纺织学报,2008,29(1):118-122.

[5] THILAGAVATHI G, NATARAJAN V. Development of a method for measurement of fabric three-dimensional drape and studies on influencing factors [J]. Indian Journal of Fibre & Textile Research, 2003, 28(1): 41-49.

[6] 陈佳,张才前,俞丹丽,等.帷幔类面料悬垂性能检测新方法研究[J].国际纺织导报,2013,41(1):71-72.

[7] 郭连朋,陈向宁,徐万朋,等.基于kinect传感器的物体三维重建[J].四川兵工学报,2014,35(11):119-123.

[8] 呙维,胡涛,朱欣焰.基于Kinect的深度数据融合方法[J].计算机应用研究,2014,31(1):285-288.

[9] 朱笑笑,曹其新,杨扬,等.一种改进的KinectFusion三维重构算法[J].机器人,2014,36(2):129-136.

[10] 朱涛,金国栋,芦利斌.Kinect应用概述及发展前景[J].现代计算机(专业版),2013(6):8-11,33.

[11] SHEN H H, HE B W, ZHANG J W, et al. Obtaining four-dimensional vibration information for vibrating surfaces with a Kinect sensor [J]. Measurement, 2015, 65: 149-165.

(责任编辑： 张祖尧)

Extraction of Characteristic Parameters of Fabric’s Unidirectional Drapability

MEIZaihuan,SHENWei,WANGYan,ZHOUHua

(Key Laboratory of Advanced Textile Materials and Manufacturing Technology,Ministry of Education, Zhejiang Sci-Tech University, Hangzhou 310018, China)

To improve the traditional measuring method for drapability and objectively reflect the drapability of fabric, a three-dimensinal (3D) measurement method for unidirectional drapability was proposed by using Microsoft Kinect Sensor in this paper. The 3D draping model was captured by Kinect Sensor and saved as STL (stereo lithographic) format files; then, the 3D draping projection was obtained by removing impurities, cutting and correcting the images; the projection drawing was intercepted horizontally to get the intercepting lines between the horizontal plane and the sample outline; such intercepting lines were systemized into a linear segment and the two-dimensional draping projection curve was obtained after filtering; the wave crest and trough point of this projection curve were recognized through related algorithm; the characterized unidirectional draping extent indexes (unidirectional draping coefficient and peak number etc.) and draping aesthetic indexes (peak symmetry coefficient etc.) were extracted; in addition, the evaluation system of unidirectional drapability was established; moreover, relevant analyses were made through experiments and standardized tests for drapability and men’s subjective assessment. The correlation analysis results show that the unidirectional fabric draping parameters on describing fabric drapability are consistent with both the traditional method and subjective evaluation method. This method realizes the 3D measurement of the fabric drapability.

fabric; drapability; draping parameters; Kinect; three-dimensional measurement; image processing

10.3969/j.issn.1673-3851.2016.05.004

2015-07-02

梅再欢(1989-)，男，湖北黄冈人，硕士研究生，主要从事纺织计算机应用方面的研究。

周华，E-mail：hzzh@zstu.edu.cn

TS107.3

A

1673- 3851 (2016) 03- 0344- 07 引用页码： 050104