A modified relation between the intraocular and intracranial pressures

Hanjing Tian,Ruiqi Du,Fan Song∗State Key Laboratory of Nonlinear Mechanics(LNM),Institute of Mechanics,Chinese Academy of Sciences,Beisihuanxi Road No.15,Beijing,100190,China



A modified relation between the intraocular and intracranial pressures

Hanjing Tian,Ruiqi Du,Fan Song∗
State Key Laboratory of Nonlinear Mechanics(LNM),Institute of Mechanics,Chinese Academy of Sciences,Beisihuanxi Road No.15,Beijing,100190,China

h i g h l i g h t s

•A novel relation between the intraocular and intracranial pressures.

•The present relation is in good agreement with the existing experiments.

•This relation overcomes the induced singularity of conventional models.

a r t i c l ei n f o

Article history:

Accepted 14 March 2016

Available online 1 April 2016

and Interdiscipline

Intraocular pressure

Intracranial pressure

Lamina cribrosa

Glaucoma

A modified relation between the intraocular and intracranial pressures is presented by employing the least square method to fit the existing experiments.Relative analysis here indicates that this modified relation not only is better than the previous relation by comparing with the existing experimental data but also overcomes the induced singularity in applying the existing mechanical models to compute the mechanical properties of the lamina cribrosa.The present study will be a beneficial help to understanding the relationship between the intraocular and intracranial pressures and even glaucomatous developing.

©2016 The Authors.Published by Elsevier Ltd on behalf of The Chinese Society of Theoretical and Applied Mechanics.This is an open access article under the CC BY-NC-ND license(http:// creativecommons.org/licenses/by-nc-nd/4.0/).

Glaucoma is the most common cause of irreversible blindness, affectingmorethan60millionpeopleworldwide,andincreasingto about80millionby2020[1].Inthecourseofdevelopingglaucoma, the difference between the intraocular pressure(IOP)and the intracranial pressure(ICP)plays a key role.It is this difference that exerts on the primary site of glaucoma-the lamina cribrosa (LC),then results in the irreversible deformation of LC,and finally induces the damage of the optic nerves passing through LC,thus triggers the visual field defect,which is medically considered to be the main pathological mechanism of glaucoma[2,3].The existing studies already prove that the glaucomatous visual field defect is positively correlated with the difference between IOP and ICP and inversely correlated with the ICP[4].Because directly observing anddeterminingthedeformationofLCandthedamageoftheoptic nerves in LC in a living body is scarcely possible in the clinical diagnosisandtreatmentofglaucoma,buildingamechanicalmodel of LC now still remains the most efficient way to understand the states of LC in vivo[5].Obviously,the relation between IOP and ICP is of the essence in correctly making the mechanical model of LC.However,the exact relation between IOP and ICP has not been understood very well yet so far.

In the existing studies of the relation between IOP and ICP, whenIOPisgreaterthan20mmHg,Quigley[3]experimentallyand clinically proved that ICP is roughly equal to 10 mmHg,i.e.

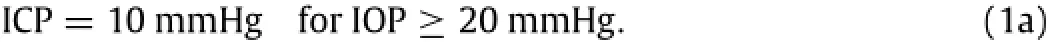
When IOP is less than 20 mmHg,on the one hand,there is not a deterministic result as Eq.(1a)deriving directly from clinic and experiment up to now,but lots of investigations indicate that ICP is significantly and positively correlated with IOP[6-10].On the other hand,in order to analyze the deformation of LC,all the existing mechanical models of LC greatly simplify the relation between IOP and ICP as a linear relation when IOP is less than 20 mmHg[5,11,12],i.e.

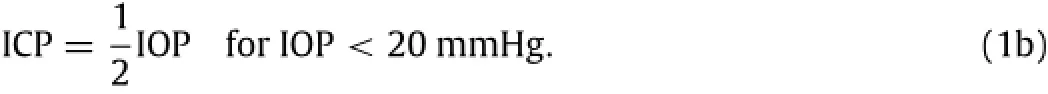
However,this simplification results directly in a serious problem:the derivatives of Eq.(1)at the point of IOP=20 mmHg are inexistence,or the rate of change of ICP at the point is discontinuousaccordingtoEq.(1),asshowninFig.1,whichfurther induces that the singularity of the deformation appears at the

http://dx.doi.org/10.1016/j.taml.2016.03.002

2095-0349/©2016 The Authors.Published by Elsevier Ltd on behalf of The Chinese Society of Theoretical and Applied Mechanics.This is an open access article under the CC BY-NC-ND license(http://creativecommons.org/licenses/by-nc-nd/4.0/).

∗Corresponding author.

E-mail address:songf@lnm.imech.ac.cn(F.Song).point in the existing mechanical model of LC[11,12],as shown in Fig.2.This can never happen in a living body.It is because that IOP is produced by the aqueous humor and ICP derives from the cerebrospinal fluid pressure.The changes of the two liquids that generate the two pressures have to be continuous in a live body.Therefore,exactly determining the relation between IOP and ICP becomes a key point in understanding the behaviors of LC.In addition,there is a big error between the values that the existing mechanical models[11,12]compute the deformations of LC according to Eq.(1)and the existing experiments measure the deformations of LC[13]when ICP is less than 20 mmHg,as shown in Fig.2.

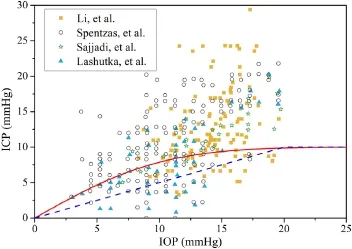
Fig.1.The relations between IOP and ICP.The broken line stands for Eq.(1), the solid line expresses Eq.(3),and different figurate points indicate the different experimental data from Refs.[6-9].The derivatives of the broken line do not exist at IOP=20 mmHg.

Here we modify the relation between IOP and ICP,and make the modified relation satisfy the three conditions:(i)at the point of IOP=20 mmHg,its derivatives are continuous;(ii)when IOP≥20 mmHg,its values are equal to the values of Eq.(1a); (iii)when IOP<20 mmHg,its values are better than those of Eq.(1b)in fitting the existing experiments.

Based on the characteristics and topography of Eq.(1),we choose a modified error function to fit the relation between IOP and ICP,namely,

First of all,according to the properties of Gauss error function andEq.(1a),themodulusofEq.(2)isreadilydeterminedasA=10.

Secondly,we use the existing experimental data between ICP and IOP to fit the other undetermined coefficient.By synthesizing the four group experimental data[6-9],we obtainα=0.088 by virtue of employing the least square method,as shown in Fig.1. Therefore,Eq.(2)is written by

The relative error between Eqs.(1a)and(3)at the point of IOP=20 mmHg is readily calculated to be 1.28%,which reaches a very good approximate in the theory of biomechanics[14].And withIOPincreasing,theerrorwillrapidlydecreaseaccordingtothe property of Gauss error function.

Further,we separately compare the root mean squared errors (RMSEs)of Eqs.(1b)and(3)with the experimental data from Refs.[6-9].All RMSE values of Eq.(3)are better than those of Eq.(1b),as shown in Table 1.

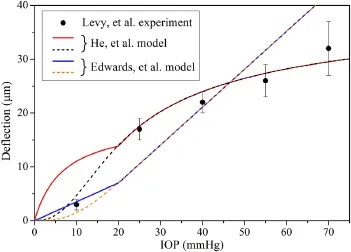
Fig.2.The deflections of LC.The solid curves stand for the results of the different mechanical models from Refs.[11,12]by employing Eq.(1),and the broken curves display the results of the different mechanical models from Refs.[11,12]by employing Eq.(3).There are the derivative singular points of the solid curves at IOP=20 mmHg.

Table 1 The RMSEs of Eqs.(1)and(3)with respect to the experiments[5-8].

Finally,employingtheexistingmechanicalmodelsofLCandthe modified relation between IOP and ICP,Eq.(3),we compute the deformations of LC,and compare these results with the existing experiments,as shown in Fig.2.Our computed results display that atthepointofIOP=20mmHg,thederivativeofthedeformationis continuous;whenIOP≥20mmHg,thedeformationsarethesame as the values obtained by using Eq.(1a);when IOP<20 mmHg, the deformations are better fit to the existing experiments than the values given by using Eq.(1b).This is an indication that the modified relation between IOP and ICP,Eq.(3),is closer to the real states than Eq.(1a)in clinic experiments.

In conclusion,based on the existing experiments,we use the least square method to obtain a modified relation between IOP and ICP.The modified relation not only is better than the previous relation by virtue of comparing with the existing experimental data,but also thoroughly overcomes the induced singularity in applying the existing mechanical model of LC to compute the mechanical properties of LC.Obviously,the present result is a beneficial help to understanding the relationship between IOP and ICP and even glaucomatous developing.

Acknowledgment

This work was supported by the National Natural Science Foundations of China(11232013 and 11472285).

References

[1]H.A.Quigley,A.T.Broman,The number of people with glaucoma worldwide in 2010 and 2020,Br.J.Ophthalmol.90(2006)262-267.

[2]H.A.Quigley,R.M.Hohman,E.M.Addicks,et al.,Morphologic changes in the lamina cribrosa correlated with neural loss in open-angle glaucoma,Am.J. Ophthalmol.95(1983)673-691.

[3]H.A.Quigley,Pathophysiology of optic nerve in glaucoma,in:J.A.McAllister, R.P.Wilson(Eds.),Glaucoma,Butterworths,London,1986,pp.30-53.

[4]R.J.Ren,J.B.Jonas,G.G.Tian,et al.,Cerebrospinal fluid pressure in glaucoma a prospective study,Ophthalmology 117(2010)259-266.

[5]T.Newson,A.El-Sheikh,Mathematical modeling of the biomechanics of the lamina cribrosa under elevated intraocular pressures,J.Biomech.Eng.-Trans. ASME 128(2006)496-504.

[6]M.K.Lashutka,A.Chandra,H.N.Murray,et al.,The relationship of intraocular pressure to intracranial pressure,Ann.Emerg.Med.43(2004)585-591.

[7]S.A.Sajjadi,M.H.Harirchian,N.Sheiklibahaei,et al.,The relation between intracranial and intraocular pressures:Study of 50 patients,Ann.Neurol.59 (2006)867-870.

[8]T.Spentzas,J.Henricksen,A.B.Patters,etal.,Correlationofintraocularpressure with intracranial pressure in children with severe head injuries,Pediatr.Crit. Care Med.11(2010)593-598.

[9]Z.Li,Y.X.Yang,Y.Lu,et al.,Intraocular pressure vs intracranial pressure in disease conditions:A prospective cohort study(Beijing iCOP study),BMC Neurol.12(2012)4.

[10]J.B.Jonas,N.L.Wang,D.Y.Yang,et al.,Facts and myths of cerebrospinal fluid pressure for the physiology of the eye,Prog.Retin.Eye Res.46(2015) 67-83.

[11]D.Q.He,Z.Q.Ren,A biomathematical model for pressure-dependent lamina cribrosa behavior,J.Biomech.32(1999)579-584.

[12]M.E.Edwards,T.A.Good,Use of a mathematical model to estimate stress and strain during elevated pressure induced lamina cribrosa deformation,Curr. Eye Res.23(2001)215-225.

[13]N.S.Levy,E.E.Crapps,Displacement of optic nerve head in response to shortterm intraocular pressure elevation in human eyes,Arch.Ophthalmol.102 (1984)782-786.

[14]Y.C.B.Fung,Elasticity of soft tissues in simple elongation,Am.J.Physiol.213 (1967)1532-1544.

9 March 2016

*This article belongs to the Biomechanics