Modeling the mechanics of HMX detonation using a Taylor-Galerkin scheme

Adam V.Duran,Veera SundararaghavanDepartment of Aerospace Engineering,University of Michigan,Ann Arbor,MI 48109,USA



Modeling the mechanics of HMX detonation using a Taylor-Galerkin scheme

Adam V.Duran,Veera Sundararaghavan∗
Department of Aerospace Engineering,University of Michigan,Ann Arbor,MI 48109,USA

h i g h l i g h t s

•An integrated algorithm for cyclotetramethylene tetranitramine(HMX)particle detonation that incorporates equations of state,Arrhenius kinetics, and mixing rules.

•A stabilized Taylor-Galerkin finite element simulation algorithm with pressure and temperature equilibrium enforced across phases.

•The scheme captures the distinct features of detonation waves:rarefaction wave,contact discontinuity,shock wave,and the von Neumann spike.

•Computed detonation velocity compares well with experiments reported in literature.

a r t i c l ei n f o

Article history:

Received in revised form

12 April 2016

Accepted 4 May 2016

Available online 17 May 2016

Energetic composites

Detonation

Shock

Finite element

Design of energetic materials is an exciting area in mechanics and materials science.Energetic composite materials are used as propellants,explosives,and fuel cell components.Energy release in these materials are accompanied by extreme events:shock waves travel at typical speeds of several thousand meters per second and the peak pressures can reach hundreds of gigapascals.In this paper,we develop a reactive dynamics code for modeling detonation wave features in one such material.The key contribution in this paper is an integrated algorithm to incorporate equations of state,Arrhenius kinetics,and mixing rules for particle detonation in a Taylor-Galerkin finite element simulation.We show that the scheme captures the distinct features of detonation waves,and the detonation velocity compares well with experiments reported in literature.

©2016 The Authors.Published by Elsevier Ltd on behalf of The Chinese Society of Theoretical and Applied Mechanics.This is an open access article under the CC BY-NC-ND license(http:// creativecommons.org/licenses/by-nc-nd/4.0/).

Energetic composite materials are used as propellants,explosives,and fuel cell components.During the detonation of these materials a shock wave is sustained by the rapid chemical energy heat release involving tightly coupled nonlinear interactions between chemistry and mechanics.These waves have extreme features which laboratory experiments are seldom equipped to handle;they travel at typical speeds of several thousand meters per second and the peak pressures can reach about 100 GPa[1]. Currently,there is significant interest in engineering the microstructures of these energetic composites for targeted shock sensitivity and energy output.Literature in this area indicate the importance of composite features,for example,smaller energetic particles have lesser run time to detonation[2]and the time to detonation increases with the strength and content of the matrix (binder)material[3].The first step in understanding these effects is the development of a reliable computational model of the energetic particle,typically the energetic crystal cyclotetramethylene tetranitramine(HMX),in these composites.

Modeling reactive burn of extreme detonation events is a significant challenge.The model is highly dependent on experimental data for each explosive composition.Unreacted material is converted to detonation products by a finite reaction rate where intermediate reactive species only exist for a few nanoseconds and are extremely difficult to measure experimentally.Reactive burn models are typically pressure(e.g.Ref.[4])or temperature dependent(e.g.Arrhenius model).Arrhenius reaction kinetics are often approximated in a single step[5]and are tuned to experiments and chemical data such as heats of formation [6-8].Equations of state are defined for each of the reaction states and mixing rules are needed for partially reacted states.Typically for the pressure dependent models,pressure equilibrium is assumed[9]or an analytic mixture is used[10]for partially burned mixture of reactants and products.For temperature based Arrhenius models,it is assumed that the unreacted explosive and reac-

http://dx.doi.org/10.1016/j.taml.2016.05.002

2095-0349/©2016 The Authors.Published by Elsevier Ltd on behalf of The Chinese Society of Theoretical and Applied Mechanics.This is an open access article under the CC BY-NC-ND license(http://creativecommons.org/licenses/by-nc-nd/4.0/).

∗Corresponding author.

E-mail address:veeras@umich.edu(V.Sundararaghavan).tion products are in both temperature and pressure equilibrium. Although timescales of interest suggest that pressure equilibrium is reached long before temperature equilibrium,both temperature and pressure equilibrium is used in this work.This assumption is widely used[5,11]and will affect partially reacted pressures and temperatures.

Shock strength of HMX is typically an order of magnitude higher than its yield strength.The material response of HMX under shock conditions is described by an isotropic equation of state(EOS)relating pressure,volume,and energy.A variety of equations of states have been proposed,the popular ones being the Jones-Wilkins-Lee(JWL)form[4],the Murnaghan form[10], and the Grüneisen form.The Grüneisen form,with a linear shock velocity versus particle velocity Hugoniot,has been employed in several studies[12-14].For the gaseous reaction products,by far the most popular equation of state is the JWL form that was developed by measuring the expansion velocity of metal casings surrounding HMX[15].

Shockwavepropagationthroughreactivematerialsisgoverned by the reactive Euler equations,a nonlinear set of hyperbolic conservation laws.Classical formulations in the fluid dynamics community use Riemann solvers in the context of finite volume methods[16,17].In the context of standard finite element methods,various methods such as Petrov Galerkin(PG)methods, Galerkin/least-squares(GLS)methods,and the Taylor-Galerkin (TG)methods have been developed.In the PG and GLS methods, a stabilization term with a coefficient is added to the weak form to act as an artificial diffusion,however,the choice of the coefficient is semi-empirical[18,19].The basic TG algorithm was proposed by Donea[20]in which Taylor expansion in time precedes the Galerkin space discretization.TG finite element schemes are especially attractive since the diffusion arises from an improved Taylor approximation(second-order)to the time derivative of the fields while increasing computational efficiency[21].While TG algorithms have been successfully applied in areas such as pollutant transport and fluid dynamics[22-24],there does not exist a prior study of the technique for detonation of energetic particles.In this paper we present a one-step second-order TG finite element scheme for modeling detonation of HMX via benchmark cases.The integrated algorithm incorporates a high resolution shock capturing scheme,multiple equations of state, Arrhenius kinetics,and mixing rules.

1.Euler equations

In detonation simulations,diffusive phenomena are neglected since pressure transfer time scales are two to three orders of magnitude faster than heat or species transfer time scales[25]. The 2D reactive Euler equations are then given by the following equations

with

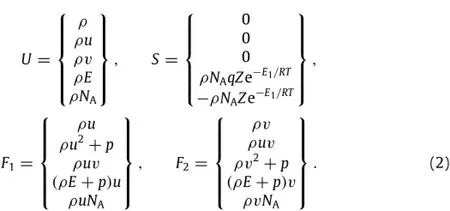
Here,ρis the density,ρu andρvare the momentum in the x and y directions,p is the pressure andρE is the total energy per unit volume.The subscripts x,y,and t denote partial derivatives. The source term S is based upon a one-step reaction scheme for HMX described by A1-→B,where NAis the mass fraction of the unreacted explosive and NBis the mass fraction of the gaseous reaction products.The reaction rate is given by the Arrhenius form in S,where q is the heat release,Z is the static frequency factor, E1is the activation energy,and R is the molar gas constant.The Euler equations are written in the quasi-linear form with Jacobian matrices Ai=∂Fi/∂U.The flux vectors are linearized as Fi=AiU for the numerical implementation.

2.Computational model

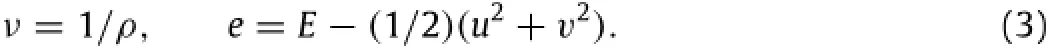
Thematerialbehaviorisgivenintheformofanequationofstate fortheunreactedsolidandtheexplosiveproducts.Theseequations arewrittenasafunctionofspecificvolumeνandenergye.Theyare related to the state variables as follows: The pressure and temperature(ps,Ts)for a solid unreacted material are given by a linear Mie-Grüneisen EOS and those for the gaseous reaction products(pg,Tg)are taken to be the JWL form. The EOS equations and the model parameters can be found in Ref.[11]and is available in a more condensed form in the supplementary file accompanying this letter.For modeling a mixture of solid and gaseous states,it is assumed that the unreacted explosive and reaction products are in temperature and pressure equilibrium;i.e.T=Ts(νs,es)=Tg(νg,eg)and p=ps(νs,es)= pg(νg,eg).Equilibriumisenforcedbyiteratingonνsandes.Thefollowing system can be solved using a Newton-Raphson method.

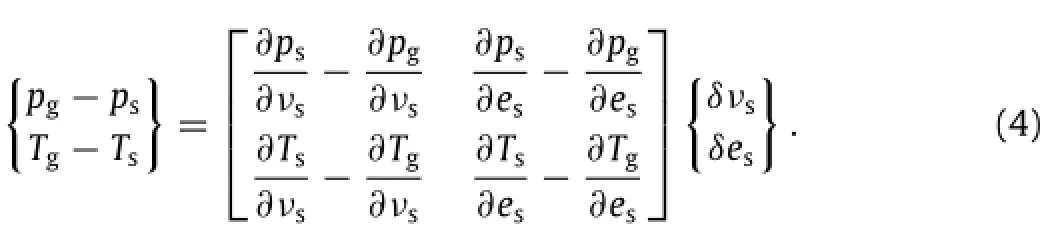
To relate the unreacted solid and reaction products,a mixture rule is used,ν=(1-λ)νs+λνgand e=(1-λ)es+λeg.Here,λ is the burn fraction;the mass fraction of detonation products in the mixture.For the one-step reaction in this work,λ=NB.Now, the system of equations is closed and both EOS can be expressed in terms of the solid specific volume and internal energy.Convergence is achieved when1p<10-4Mbar(1 bar=105Pa)and 1T<10-2K as discussed in Ref.[11].

The2DreactiveEulerequationsgivenbyEq.(1)aresolvedusing aone-stepTGscheme.Thiswidelyusedtime-steppingalgorithmis second-orderaccurate,explicitandanalogoustotheLax-Wendroff method[20].Taking a Taylor series expansion of U(from Eq.(2)) in time,

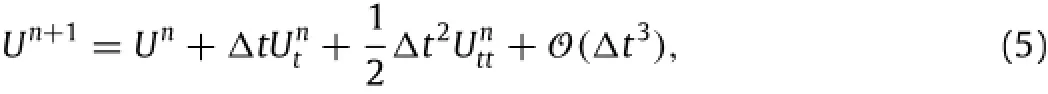
where1t is the time step,superscripts n+1 denotes the current time and n denotes the previous time.The second term of the right hand side of Eq.(5)is found from rearranging Eq.(1)and the third term is found by differentiating Eq.(1)with respect to time.Now Eq.(5)is written as

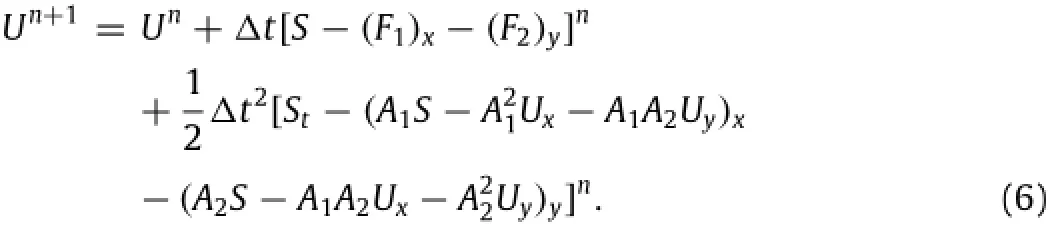
Ateachtimestep,theequationsofstateandthemixingruleisused to compute Aiand the source terms.The field variables are solvedusing the weak form given as follows:

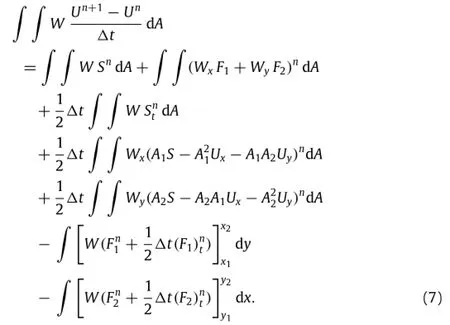
Toensurestabilityinregionsofcompressionwhere∂u/∂x<0and∂v/∂y<0,flux is computed based on a group representation.AfterGalerkinspatialdiscretizationthealgebraicequationM(Un+1-Un)=Bnis obtained and solved for Un+1.A lumping scheme is then used for the purpose of adding numerical dissipation and to givenon-oscillatorysolutionsinthepresenceofsteepsolutiongradients[26].Here,the consistent mass matrix M is replaced by the diagonal matrix ML,obtained by row sum.The mass lumping reducesthesecondorderTGschemetoafirstorderscheme.Addition of a small first order solution adds an artificial numerical dissipation to the system.The smoothed solution is obtained by adding a small dissipation through parameter d,where 0≤d≤1;for maximum dissipation d=1.The smoothed solution is obtained as

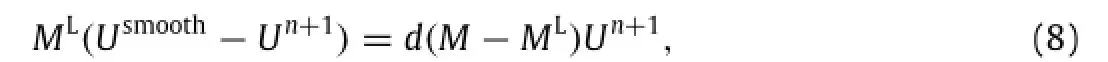
where d is locally constructed by considering pressure gradients as expressed in the equations below.Here,nodes''j''are connected to nodes''i''wherep()denoteslocalpressureandx()denoteslocalposition.

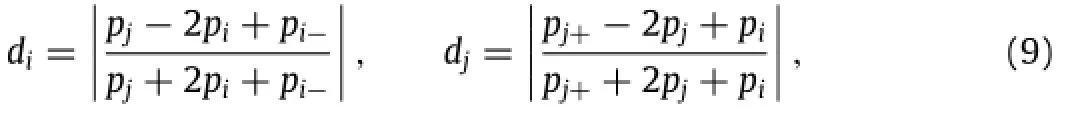
where

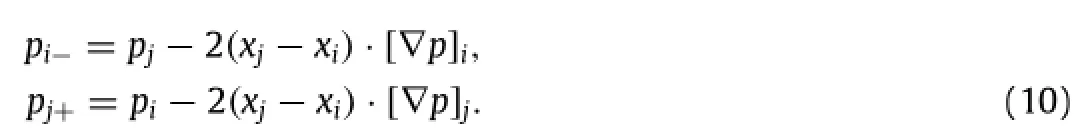
Then,the artificial viscosity coefficient for segment i-j is determined by the following equation,whereχis a free parameter discussed in the following section.

3.Verification using SOD shock benchmark problem

Totestthestabilityandaccuracyoftheschemedescribedabove, the classical fluid dynamics shock tube problem is solved[27].The test consists of two fluids at differing pressures separated by a membrane.Once the membrane is removed,a rarefaction wave contactdiscontinuityandshockwaveisformed.Thesolutionforan ideal gas is obtained analytically using Riemann invariants and is compared with numerical results in Fig.1.The numerical results in Fig.1showgoodagreementwiththeexactsolutionandthedistinct characteristics of the test are captured.Next,the effects of the free parameterχon the numerical solution are studied.Figure 2 shows theaverageerror pernodeasafunctionoftheparameterχfortwo different time steps.In general,error increases with increasing the parameterχand decreasing the time step increases the average error per node.The optimal parameter for both time steps isχ= 0.1,the value used in Fig.1 and in subsequent sections.

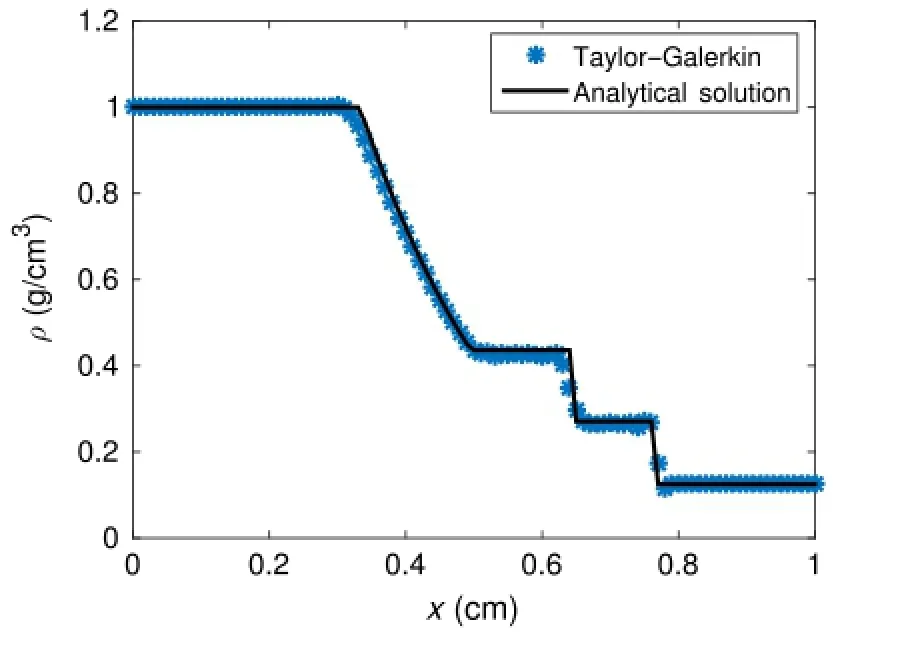
Fig.1.Numerical and analytical results for SOD shock tube.

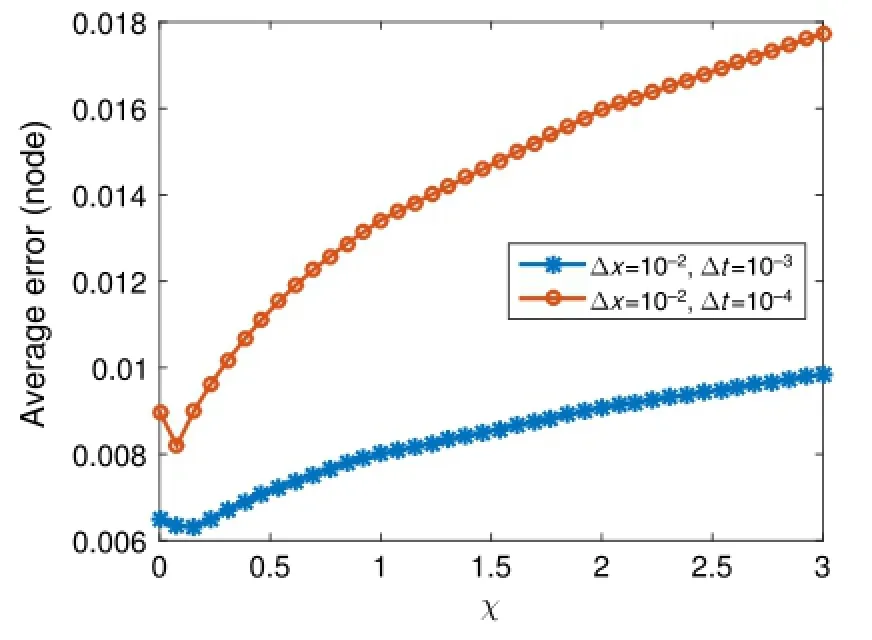
Fig.2.Effect of parameterχon average error per node.

4.Reactive HMX models in 1D and 2D

Next,shock loading a single HMX sample is studied.Numerical results are obtained with linear elements for a 1 cm domain with 1x=0.01 cm and1t=10-3µs.Dirichlet boundary conditions areusedwherevelocityisspecifiedtobezero.Discontinuousinitial conditions are given for density and total energy.For the left half of the domainρ=2.2 g/cm3and E=0.004 Mbar resulting in a pressure of p=5 GPa and temperature of T=590 K. The right half of the domain is set to ambient conditions where ρ=ρ0=1.89 g/cm3and E=0.00 Mbar resulting in a pressure of p=0 GPa and temperature of T=295 K.Velocity is initially zero and the sample is purely solid with a mass fraction of unity.Numerical results are shown in Figs.3 and 4 at time steps of t=0.2µs for a duration of one microsecond.Figure 3 shows the density of the sample.As the solution progresses a rarefaction wave,contact discontinuity,and shock wave form.The shock wave travels through the right side of the domain with a value ofρ= 2.07 g/cm3.Behind the shock and discontinuity,the initial density drops to a value ofρ=2.04 g/cm3as the solution evolves.At time t=1µs,the rarefaction wave is located at 0.1 cm,the contact discontinuity is located at 0.53 cm and the shock wave is located at 0.85 cm.Velocity reaches a maximum of u=0.03 cm/µs during the simulation.Figure 4 shows the pressure of the HMX sample. The initial pressure drops from p=5 GPa to p=2.13 GPa and is maintained through the shock front.The initial shock conditions are not drastic enough to initiate detonation of the sample withinthe simulated duration of t=1µs.The mass fraction never falls below NA=0.99 and the material remains inert.The computed shock velocity of the system is 0.36 cm/µs(p=5 GPa)and agrees with values reported in literature for experiments with HMX particle composites.Shot#1120 in Ref.[28]reports a shock velocity of 0.39 cm/µs for an input pressure of p=4.91 GPa.

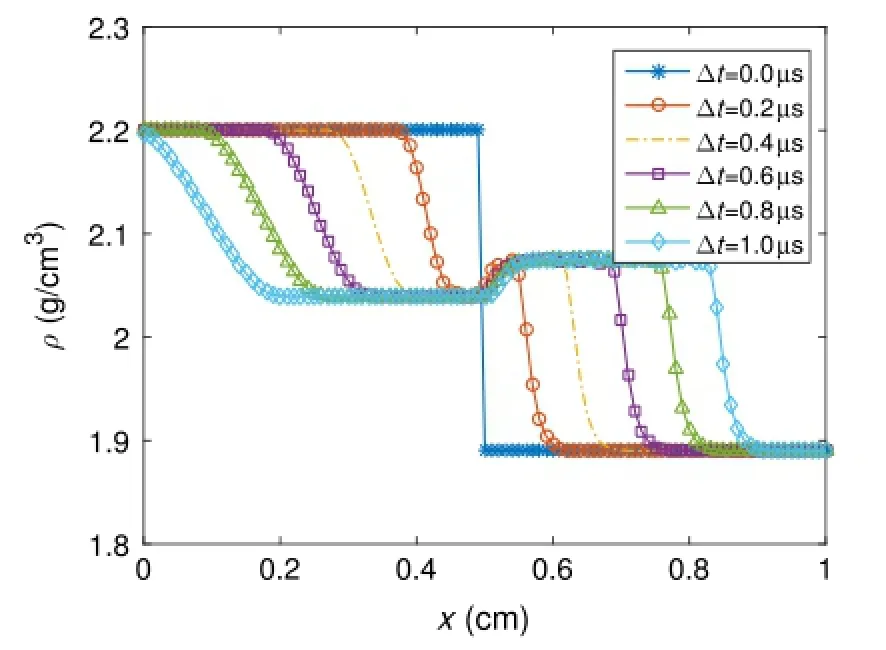
Fig.3.Numerical results of density for HMX sample at t=0.2µs time steps.

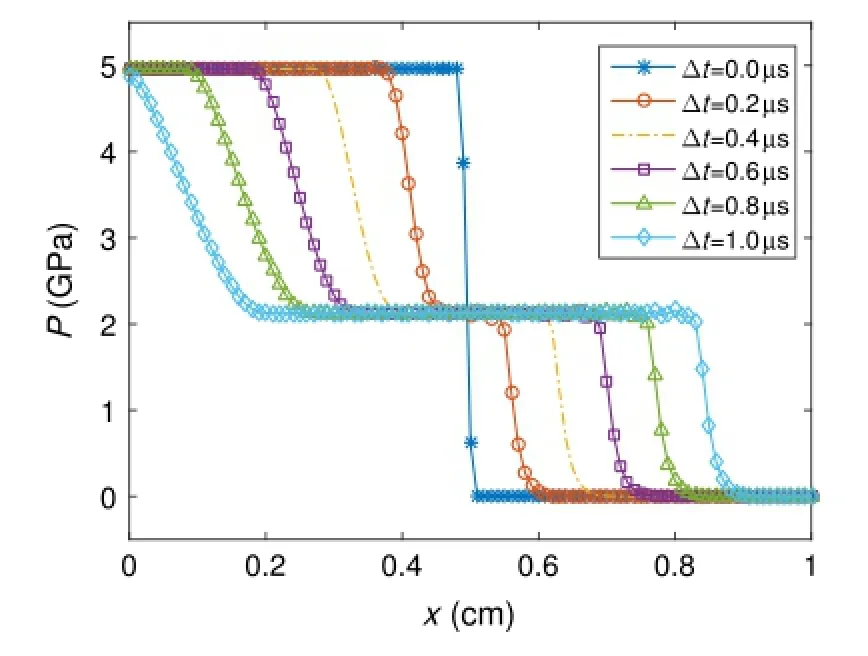
Fig.4.Numerical results of pressure for HMX sample at t=0.2µs time steps.

Next,detonation of 1 cm by 1 cm HMX sample is studied.A uniform mesh with a1x=1y=0.01 cm and1t=10-4µs is usedforadurationoft=0.45µs.No-slipboundaryconditionsare considered;i.e.u=0 at x=[0,1]cm andv=0 at y=[0,1]cm. A circular detonation front was used with the initial discontinuity located at r=0.1 cm.The combustion front is represented as a quarter of a circle that expands as the detonation proceeds.Within the quarter circle the material is shocked to a pressure of p= 55 GPa and temperature of T=2100 K.Outside,the domain is set to ambient conditions.Figure 5 shows the temperature profile at t=0.4µs.The temperature wave reaches a maximum value of T=3300 K and is sufficient enough to prompt detonation.Along the 45◦plane shown in Fig.5 the burn fraction of the material λis plotted at time intervals of t=0.045µs in Fig.6.Within t=0.045µsthesolidwithinthequartercircleisfullyburnt.Asthe solution progresses the shock wave travels through the solid HMX sample and becomes fully gaseous.The calculated shock speed of 1.53 cm/µs is much higher than the previous inert case due to detonation.

This paper presented the one-step second-order Taylor-Galerkin finite element scheme for modeling detonation of HMX via benchmark cases.The integrated algorithm incorporates a high resolution shock capturing scheme,multiple equations of state,Arrhenius kinetics,and mixing rules for HMX detonation simulations.In the detonation model,a one-step reaction scheme was used and temperature and pressure equilibrium between

partially reacted states was enforced with a Newton-Raphson method and rule of mixtures.The numerical scheme was tested and agreed with exact solutions for SOD shock tube problem.The test was repeated for a single HMX sample and we showed that the shock velocity compared well with the experimental range reported in literature.Future work will include adding equations for a polymeric binder to simulate detonation in particulate composite microstructures.

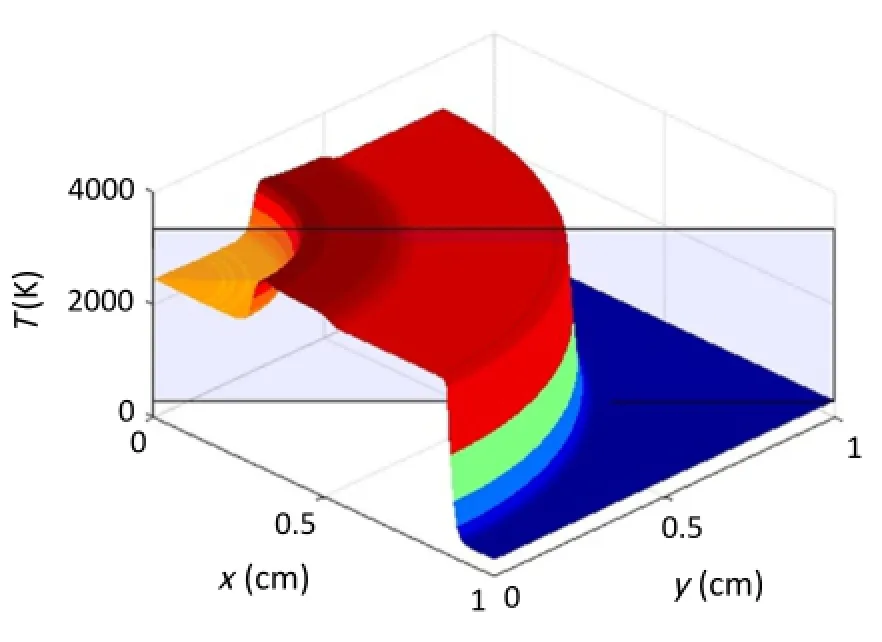
Fig.5.Numerical results of temperature at t=0.4µs.

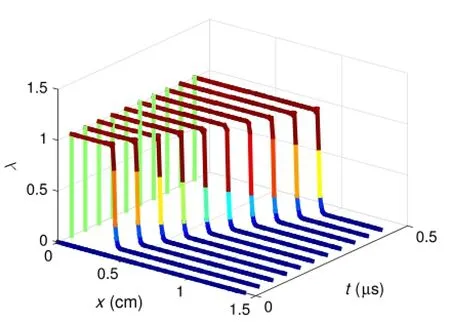
Fig.6.Numerical results of burn fraction along 45◦plane at t=0.045µs time steps.

Acknowledgments

This paper was based upon work supported by the National Science Foundation Graduate Research Fellowship Program(DGE 1256260)and The Defense Threat Reduction Agency(HDTRA1-31-1-0009).

Appendix A.Supplementary data

Supplementary material related to this article can be found online at http://dx.doi.org/10.1016/j.taml.2016.05.002.

References

[1]W.Fickett,W.C.Davis,Detonation,University of California Press,Berkeley, 1979.

[2]M.F.Gogulya,M.N.Makhov,A.Y.Dolgoborodov,et al.,Mechanical sensitivity and detonation parameters of aluminized explosives,Combust.Explos.Shock Waves 40(2004)445-457.

[3]Z.P.Duan,L.J.Wen,Y.Liu,et al.,A pore collapse model for hot-spot ignition in shocked multi-component explosives,Int.J.Nonlinear Sci.Numer.Simul.11 (2010)19-24.

[4]E.L.Lee,C.M.Tarver,Phenomenological model of shock initiation in heterogeneous explosives,Phys.Fluids(1958-1988)23(1980)2362-2372.

[5]R.Menikoff,DetonationwavesinPBX9501,Combust.TheoryModel.10(2006) 1003-1021.

[6]R.R.McGuire,C.M.Tarver,Chemical decomposition model for the thermal explosion of confined hmx,rdx and tnt explosives,in:Seventh Symposium (International)on Detonation NSWC MP,82(1981)56-64,334.

[7]C.M.Tarver,T.D.Tran,Thermal decomposition models for hmx-based plastic bonded explosives,Combust.Flame 137(2004)50-62.

[8]B.F.Henson,L.Smilowitz,J.J.Romero,et al.,Modeling thermal ignition and the initial conditions for internal burning in pbx 9501,AIP Conf.Proc.1195(2009) 257-262.

[9]M.Cowperthwaite,A constitutive model for calculating chemical energy release rates from the flow fields in shocked explosives,in:Seventh Symposium(International)onDetonation,Annapolis,MD,82(1981)498-505, 34.

[10]P.C.Souers,S.Anderson,J.Mercer,et al.,JWL++:a simple reactive flow code packagefordetonation,Propellants,Explosives,Pyrotechnics25(2000)54-58.

[11]C.A.Handley,Numerical modelling of two HMX-based plastic-bonded explosives atthe mesoscale(Ph.D.thesis),University of St.Andrews,UK,2011.

[12]M.R.Baer,Computational modeling of heterogeneous reactive materials at the mesoscale,AIP Conf.Proc.505(2000)27-34.

[13]P.A.Conley,D.J.Benson,P.M.Howe,Microstructural effects in shock initiation, in:Eleventh International Detonation Symposium,Office of Naval Research ONR 33300-5,Snowmass,CO,1998,pp.768-780.

[14]R.Menikoff,E.Kober,Compaction waves in granular HMX,AIP Conf.Proc.505 (2000)397-400.

[15]J.W.Kury,H.C.Hornig,E.L.Lee,etal.Metalaccelerationbychemicalexplosives, in:Fourth(International)Symposium on Detonation,ACR-126,1965.

[16]J.M.McGlaun,S.L.Thompson,M.G.Elrick,CTH:a three-dimensional shock wave physics code,Int.J.Impact Eng.10(1990)351-360.

[17]A.L.Brundage,R.R.Wixom,A.S.Tappan,et al.,Mesoscale simulations of shock initiation in energetic materials characterized by three-dimensional nanotomography,AIP Conf.Proc.1195(2009)315-318.

[18]W.H.Raymond,A.Garder,Selective damping in a galerkin method for solving wave problems with variable grids,Mon.Weather Rev.104(1976) 1583-1590.

[19]A.N.Brooks,T.J.Hughes,Streamline upwind/Petrov-Galerkin formulations for convection dominated flows with particular emphasis on the incompressible Navier-Stokes equations,Comput.Methods Appl.Mech.Engrg.32(1982) 199-259.

[20]J.Donea,A Taylor Galerkin method for convective transport problems, Internat.J.Numer.Methods Engrg.20(1984)101-119.

[21]E.A.Thornton,R.Ramakrishnan,Supercomputer implementation of finite element algorithms for high speed compressible flows,NASA-CR-177065, NASA technical report,United States,1986.

[22]V.Nassehi,J.H.Bikangaga,A mathematical model for the hydrodynamics and pollutants transport in long and narrow tidal rivers,Appl.Math.Model.17 (1993)415-422.

[23]M.Quecedo,M.Pastor,A reappraisal of taylor galerkin algorithm for drying wetting areas in shallow water computations,Int.J.Numer.Methods Fluids 38(2002)515-531.

[24]R.Lohner,K.Morgan,J.Peraire,et al.,Finite element flux corrected transport (FEM-FCT)for the euler and Navier Stokes equations,Internat.J.Numer. Methods Fluids 7(1987)1093-1109.

[25]J.E.Reaugh,Computer simulations to study the high-pressure deflagration of HMX,AIP Conf.Proc.706(2004)401-404.

[26]J.Donea,A.Huerta,Finite element methods for flow problems,first ed.,John Wiley and Sons,Chichester(West Sussex),England,2003.

[27]G.A.Sod,A survey of several different methods for systems of nonlinear hyperbolic conservation laws,J.Comput.Phys.27(1978)1-31.

[28]R.E.Winter,S.S.Sorber,D.A.Salisbury,et al.,Experimental study of the shock response of an HMX-based explosive,Shock Waves 15(2006)89-101.

23 January 2016

*This article belongs to the Fluid Mechanics