On the stress-strain states of cellular materials under high loading rates
2016-09-14YunyunDingShilongWngZhijunZhengLimingYngJilinYuCASKeyLortoryofMechniclBehviorndDesignofMterilsUniversityofSciencendTechnologyofChinHefei230026ChinMechnicsndMterilsScienceReserchCenterNingoUniversityNingo315211Chin
Yunyun Ding,Shilong Wng,Zhijun Zheng,∗,Liming Yng,Jilin YuCAS Key Lortory of Mechnicl Behvior nd Design of Mterils,University of Science nd Technology of Chin,Hefei 230026,ChinMechnics nd Mterils Science Reserch Center,Ningo University,Ningo 315211,Chin
Letter
On the stress-strain states of cellular materials under high loading rates
Yuanyuan Dinga,Shilong Wanga,Zhijun Zhenga,∗,Liming Yangb,Jilin Yua
aCAS Key Laboratory of Mechanical Behavior and Design of Materials,University of Science and Technology of China,Hefei 230026,China
bMechanics and Materials Science Research Center,Ningbo University,Ningbo 315211,China
h i g h l i g h t s
•Dynamic impact of cellular materials is analyzed with wave propagation technique.
•Time history of particle velocity and stress-strain history curves are obtained.
•The dynamic stress-strain states obtained verify the validity of the dynamic-rigid-plastic hardening(D-R-PH)model.
a r t i c l ei n f o
Article history:
Accepted 3 May 2016
Available online 10 May 2016
Cellular materials
Stress-strain states
Lagrangian analysis method
Shock wave
A virtual Taylor impact of cellular materials is analyzed with a wave propagation technique,i.e.the Lagrangian analysis method,of which the main advantage is that no pre-assumed constitutive relationshipisrequired.Timehistoriesofparticlevelocity,localstrain,andstressprofilesarecalculatedto present the local stress-strain history curves,from which the dynamic stress-strain states are obtained. The present results reveal that the dynamic-rigid-plastic hardening(D-R-PH)material model introduced in a previous study of our group is in good agreement with the dynamic stress-strain states under high loading rates obtained by the Lagrangian analysis method.It directly reflects the effectiveness and feasibility of the D-R-PH material model for the cellular materials under high loading rates.
©2016 The Author(s).Published by Elsevier Ltd on behalf of The Chinese Society of Theoretical and Applied Mechanics.This is an open access article under the CC BY license(http://creativecommons.org/ licenses/by/4.0/).
Cellular materials have been extensively used in crashworthiness application due to their considerable capacity of energy absorption[1-4].The stress-strain relation of cellular materials under low-velocity compression shows three distinct stages of deformation,namely elastic,long plateau,and densification stages. The dynamic behavior of cellular materials under high-velocity loading is dominated by inertia effect,which leads to the deformation localization and stress enhancement[5].The dynamic features can be well explained by the 1D shock wave models[5-8], in which the rigid-perfectly plastic-locking(R-PP-L)shock wave model involving only two material parameters(locking strainεLand plateau stressσpl)is the most popular one.However,the RPP-L shock wave model can only characterize the compressive behavior of cellular materials in a first-order approximation[9,10]. Recently,Zheng et al.[11]proposed a rigid-plastic hardening (R-PH)material model(an R-PH idealization)and a dynamicrigid-plastic hardening(D-R-PH)material model(a D-R-PH idealization)to describe the stress-strain behaviors of cellular materialsunderlow-velocitycompressionandunderhigh-velocity impact,respectively,and revealed different deformation mechanisms to explain the loading-rate effect of cellular materials.The stress-strain relation of the D-R-PH idealization[11]is written as

whereσ0dis the dynamic initial crushing stress and D the strain hardening parameter.They found that the stress-strain states of cellular materials are essentially loading-rate dependent[11].In this study,we aim to present further evidence on the loading-rate effect of cellular materials.
In the shock wave models for cellular materials[5-11],the shock wave assumption is an idealizedassumption,which is appropriateonlyforthecasewitharelativelyhighimpactvelocity. The wave propagation technique may provide an opportunity to investigate the strain-stress behavior of cellular materials without any pre-assumptions.The Lagrangian analysis method[12-14] gets the favor of most researchers because no constitutive relation is required.However,the boundary/initial conditions arerequired for the traditional Lagrangian analysis method as it involves integral operations.To overcome this difficulty,a method combining the Hopkinson pressure bar technique and Lagrangian analysis was developed by Wang et al.[15],from which the physical quantities(particle velocity,stress,etc.)at the boundary of the specimen can be obtained simultaneously.This wave propagation technique,namely the''1sv+nv''Lagrangian method, contains a dual-information of stress and velocity at one position often located at the boundary of specimen and n particle velocity profiles.Due to the big difference in wave impedance between the elastic bar and cellular materials,another experimental technique (Taylor-Hopkinson bar with knowing initial conditions)[16]was carriedouttoinvestigatethedynamicresponseofaluminumfoam. Unfortunately,the experimental data of cellular materials under high impact velocity,sayv>200 m/s,are hardly obtained and the other limitations like the digital image correlation accuracy also restrictitsapplication.Tomakeupthedeficienciesinexperimental study,the mesoscopic finite element(FE)model is employed in this paper and the Lagrangian analysis is applied to study the stress-strain behavior of cellular materials under high-velocity impact.
In 1D stress wave propagation theory[17],the mass and momentum conservation conditions in Lagrangian coordinate are expressed as and


respectively,wherev,ε,andσare particle velocity,strain,and stress,respectively;X is Lagrangian coordinate;t is time;ρ0is the initial density of cellular specimen.Here,the stress and strain are defined as positive for compressive case,and negative for tensile case.Eqs.(2)and(3)are the basic equations of the Lagrangian analysis method,from which the stress and strain relation can be built with the aid of particle velocity field.Since the variables are connected by their first-order partial derivatives,the integral operations are requisite and the boundary/initial conditions are required to determine the integral constants.Supposing detailed information of particle velocityv(Xi,tj)at Lagrangian coordinates Xi(i=1,2,...,n)and time tj(j=1,2,...)has been measured, and then the strain and stress fields can be determined from Eqs. (2)and(3),written in the difference form
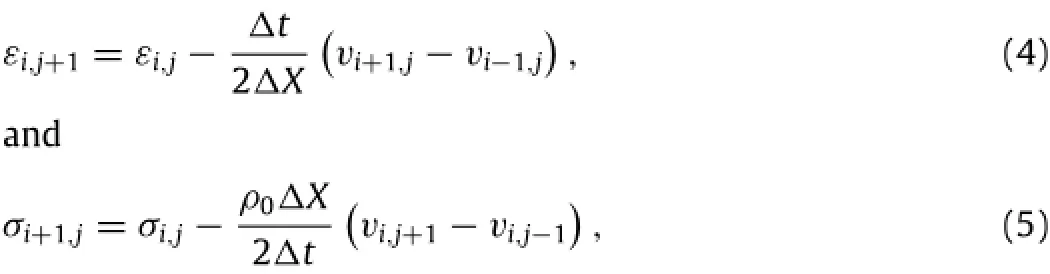
where1X is the grid size and1t the time step.It is worth noticing that the partial derivatives(∂σ/∂X and∂v/∂X)may be inaccurate whenthedistanceoftwoadjacentLagrangianpositionsisnotsmall enough,as for most experimental cases.Grady[14]introduced the path-line method to improve the computational accuracy of Lagrangian analysis,in which the first order derivatives containing variableX ischangedtothepartialderivativescontainingvariablet by the total differentiation along the path-line.If there is sufficient data obtained from a test,the path-line method is not necessary. The FE simulations can offer a detailed particle velocity field and the boundary stress.
The mesoscopic FE model[11]is employed to perform the quasi-staticcompressionanddynamicimpactofcellularmaterials. Closed-cell foam models are generated by employing the 3D Voronoi technique,see Ref.[11]for details.The cell-wall material of the Voronoi structure is assumed to be elastic,perfectly plastic with densityρs=2770 kg/m3,Young's modulus E=69 GPa, Poisson's ratioν=0.3,and yield stressσys=170 MPa.The relative density of the Voronoi structure used isρ0/ρs=0.1 and cell walls have a uniform thickness.The cellular specimen used in this study is constructed in a volume of 30X20X 20 mm3with 600 nuclei,and the average cell size d≈3.34 mm. The ABAQUS/Explicit software is used to perform the numerical simulations.

Fig.1.The Taylor impact test scenario and deformation patterns.
A Taylor impact test scenario of cellular materials is performed, as schematically represented in Fig.1.In the virtual test,the specimen travels at an initial velocityv0=250 m/s and impacts a fixed rigid target.Some deformation patterns are presented in Fig.1.The velocity profiles at all element nodes can be extracted from the FE simulations,and the stress,strain,and velocity profiles at free end can also be acquired simultaneously.Supposing the X coordinateisestablishedatthefreeendandtheareaofspecimenis considered to be unchanged throughout the test,then the dynamic strain-stress states can be investigated by using the''1sv+nv'' Lagrangian analysis method.
In considering the fact that the Lagrangian analysis method is based on the continuum mechanics,an average particle velocity field is used to substitute for the local particle velocity.For example,the average velocity profile at the Lagrangian position X is calculated by averaging all nodal velocities along the loading direction from X-d/2 to X+d/2 in the cellular specimen.The particle velocity profilesv(Xi,t)are shown in Fig.2(a).A feature of rapid velocity change can be observed,which is a result of the propagation of plastic stress waves.In the specimen,unloading waves are continually reflected back from the free end,and thus the plastic wave becomes weaken and finally vanished,which can be illustrated by the disappearance of rapid velocity change at position X<8 mm.
Thus,according to the''1sv+nv''Lagrangian analysis method mentioned above,the dynamic strain and stress profiles can be directly obtained by the particle velocity field combining with ε(X,0)=0 andσ(0,t)=0.As shown in Fig.2(b),the strain at a Lagrangian position X≥8 mm increases rapidly at first and then maintains a specific strain.This local specific strain decreases with the position away from the impact end and reflects the degree of local densification induced by the action of the plastic wave in the specimen.However,for the position of X<8 mm,the strain is almost equal to zero because of the disappearance of plastic wave in those positions there.
From Eq.(5),the obtained stress profiles,as shown in Fig.2(c), can be divided into three stages,namely the elastic,plastic,and unloading stages.As can be seen,in the elastic stage,the stress profile increases dramatically from zero to a dynamic crushing stress.Then,with the action of plastic wave,the stress gradually increases further to a densification stress,and afterwards the stress begins to decrease due to the action of the unloading wave.Moreover,the densification stress decreases with the distance away from the impact boundary,which also reflects the process that the plastic wave is gradually weakened by the elastic unloading wave.In Ref.[11],only the stress at the impact end was obtained.Althoughthelocalstraindistributioncanbecalculatedin Ref.[11],the absence of the local stress distribution does not bring a full understanding of the local stress-strain history of a position in the specimen.
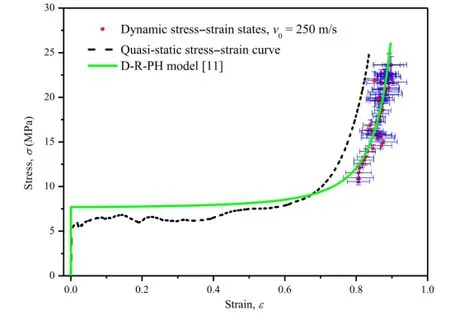
By eliminating the time from the stress and strain profiles,a local dynamic stress-strain history curve can be acquired at each Lagrangian position,as shown in Fig.3 with dash lines.In these localstress-strainhistorycurves,threedistinctstages,i.e.,theelastic,plastic,and unloading stages,can be observed.The elastic and unloading stages are mainly controlled by the Young's modulus of cellularmaterials,andthesetwostagesareapproximatelyinparallel.For the Lagrangian positions X≥14 mm,at which the loading rate is quite high,the stress in plastic stage almost increases linearly from the dynamic crushing stress to the densification stress, buttheplasticdeformationoccursalongacrookedlineundermoderate loading rates(corresponding to 8 mm Under high loading rates,the deformation pattern of cellular materials consists of lay-wise collapse bands,which is similar with the phenomenon of structural shock wave[18].It suggests the dynamic response of cellular materials can be characterized by the shock wave models under high loading rates.The D-RPH idealization with two material parameters,see Eq.(1),can welldepictthedynamicconstitutivebehaviorofcellularmaterials. As reported in Ref.[11],the material parameters of the D-R-PH idealization are obtained based on the local strain field[19,20], boundary stress and conservation conditions(=7.7 MPa and D=0.22 MPa). Fig.2.Time histories of(a)particle velocity,(b)local strain,and(c)local stress of the cellular material under initial impact velocity of 250 m/s. Fig.3.The local stress-strain history profiles and the dynamic stress-strain states for the cellular material. Three stress-strain curves for the cellular material considered are presented in Fig.4:the dash line is obtained from the quasistatic compression simulation,the solid line is the D-R-PH model presented by Zheng et al.[11],and the points with error bars are the dynamic stress-strain states obtained by Lagrangian analysis methodunderhighloadingrates.TheD-R-PHmodelcoincideswell withthestress-strainstatesobtainedbyLagrangianmethodunder high loading rates.It reveals the effectiveness and reliability of the D-R-PH model for cellular materials under high loading rates.The densification strain under a high loading rate is larger than quasistatic one and the dynamic initial crushing stress is also higher than that of quasi-static.These phenomena are connected with the different deformation mechanisms under different loading rates[11].Applying the Lagrangian analysis method,we present much direct evidence and confirm the findings of Zheng et al.[11].It should be noted that the Lagrangian analysis method does not involve the assumption of deformation patterns.Thus, the Lagrangian analysis method may be applied to explore the rate-sensitivity mechanism of cellular materials under moderate loading rates. In the present study,we carried out a virtual Taylor test combining with the Lagrangian analysis method to explore the dynamic behavior of cellular materials.With the aid of freeend boundary condition,a serial of local stress-strain history curves can be determined from the particle velocity field by the Lagrangian analysis method.Furthermore,a curve of dynamic stress-strain states is obtained from the critical points just before the unloading stage of local stress-strain history curves.Under high loading rates,the prediction of D-R-PH model[11]coincides well with the dynamic stress-strain states obtained by applying the Lagrangian analysis method.Thus,the effectiveness and reliability of the D-R-PH model for cellular materials under high loading rates can be further confirmed. Fig.4.Comparison of the quasi-static stress-strain curve,dynamic stress-strain states,and the D-R-PH model for the cellular material. This work was supported by the National Natural Science Foundation of China(11372308 and 11372307)and the Fundamental Research Funds for the Central Universities(WK2480000001). References [1]A.G.Hassen,L.Enstock,M.Langseth,Close-range blast effects of aluminum foam panels,Int.J.Impact Eng.27(2002)593-618. [2]X.K.Wang,Z.J.Zheng,J.L.Yu,Crashworthiness design of density-graded cellular metals,Theor.Appl.Mech.Lett.3(2013)031001. [3]S.F.Liao,Z.J.Zheng,J.L.Yu,et al.,A design guide of double-layer cellular claddings for blast alleviation,Int.J.Aerosp.Lightweight Struct.3(2013) 109-133. [4]S.L.Lopatnikov,B.A.Gama,M.J.Haque,et al.,Dynamic of metal foam deformation during taylor cylinder-hopkinson bar impact experiment, Compos.Struct.61(2003)61-71. [5]S.R.Reid,C.Peng,Dynamic uniaxial crushing of wood,Int.J.Impact Eng.19 (1997)531-570. [6]Z.J.Zheng,Y.D.Liu,J.L.Yu,et al.,Dynamic crushing of cellular materials: Continuum-based wave models for the transitional and shock modes,Int.J. Impact Eng.42(2012)66-79. [7]L.L.Wang,L.M.Yang,Y.Y.Ding,On the energy conservation and critical velocities for the propagation of a steady-shock wave in a bar of cellular material,Acta Mech.Sin.29(2013)420-428. [8]Z.J.Zheng,J.L.Yu,C.F.Wang,et al.,Dynamic crushing of cellular materials:A unified framework of plastic shock wave model,Int.J.Impact Eng.53(2013) 29-43. [9]J.J.Harrigan,S.R.Reid,C.Peng,Inertia effects in impact energy absorbing materials and structures,Int.J.Impact Eng.22(1999)955-979. [10]P.J.Tan,S.R.Reid,J.J.Harrigan,et al.,Dynamic compressive strength properties of aluminum foams.Part II-'shock'theory and comparison with experimental data and numerical models,J.Mech.Phys.Solids 53(2005)2206-2230. [11]Z.J.Zheng,C.F.Wang,J.L.Yu,etal.,Dynamicstress-strainstatesformetalfoams using a 3D cellular model,J.Mech.Phys.Solids 72(2014)93-114. [12]R.Fowles,R.F.Williams,Plane stress wave propagation in solids,J.Appl.Phys. 41(1970)360-363. [13]M.Cowperthwaite,R.F.Williams,Determination of constitutive relationships with multiple gauges in non-divergent waves,J.Appl.Phys.42(1971) 456-462. [14]D.E.Grady,Experimental analysis of spherical wave propagation,J.Geophys. Res.78(1973)1299-1307. [15]L.L.Wang,J.Zhu,H.W.Lai,A new method combining lagrangian analysis with hpb technique,Strain 47(2011)173-182. [16]L.L.Wang,Y.Y.Ding,L.M.Yang,Experimental investigation on dynamic constitutive behavior of aluminum foams by new inverse methods from wave propagation measurements,Int.J.Impact Eng.62(2013)48-59. [17]L.L.Wang,Foundations of Stress Waves,second ed.,National Defense Industry Press,Beijing,2005. [18]T.Y.Reddy,S.R.Reid,R.Barr,Experimental investigation of inertia effects in one-dimensional metal ring systems subjected to end impact-II.Free-ended systems,Int.J.Impact Eng.11(1991)463-480. [19]S.F.Liao,Z.J.Zheng,J.L.Yu,On the local nature of the strain field calculation method for measuring heterogeneous deformation of cellular materials,Int.J. Solids Struct.51(2014)478-490. [20]S.F.Liao,Z.J.Zheng,J.L.Yu,Dynamic crushing of 2D cellular structures:Local strain field and shock wave velocity,Int.J.Impact Eng.57(2013)7-16. 25 March 2016 http://dx.doi.org/10.1016/j.taml.2016.05.001 2095-0349/©2016 The Author(s).Published by Elsevier Ltd on behalf of The Chinese Society of Theoretical and Applied Mechanics.This is an open access article under the CC BY license(http://creativecommons.org/licenses/by/4.0/). ∗Corresponding author. E-mail address:zjzheng@ustc.edu.cn(Z.Zheng). *This article belongs to the Solid Mechanics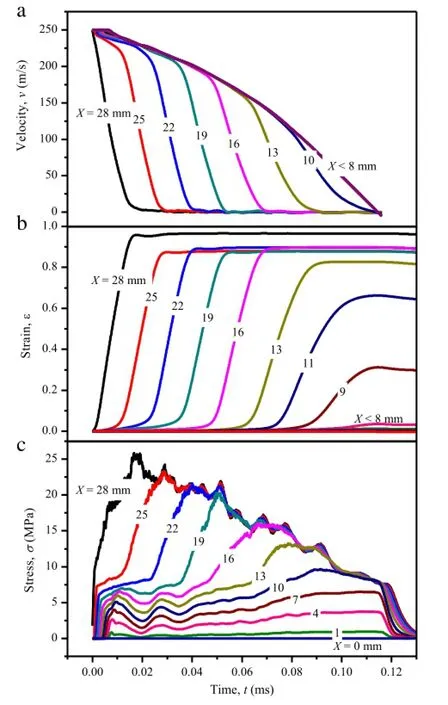

Acknowledgments
杂志排行
Theoretical & Applied Mechanics Letters的其它文章
- Heat transport in low-dimensional materials:A review and perspective
- Performance of global look-up table strategy in digital image correlation with cubic B-spline interpolation and bicubic interpolation
- Estimation of extreme wind speed in SCS and NWP by a non-stationary model
- Modeling the mechanics of HMX detonation using a Taylor-Galerkin scheme
- Numerical investigation of air-entrainment in skimming flow over stepped spillways
- A modified relation between the intraocular and intracranial pressures
