Performance of global look-up table strategy in digital image correlation with cubic B-spline interpolation and bicubic interpolation

Zhiwei Pan,Wei Chen,Zhenyu Jiang∗,Liqun Tang,Yiping Liu,Zejia LiuState Key Laboratory of Subtropical Building Science,School of Civil Engineering and Transportation,South China University of Technology,Guangzhou 510640,China



Performance of global look-up table strategy in digital image correlation with cubic B-spline interpolation and bicubic interpolation

Zhiwei Pan,Wei Chen,Zhenyu Jiang∗,Liqun Tang,Yiping Liu,Zejia Liu
State Key Laboratory of Subtropical Building Science,School of Civil Engineering and Transportation,South China University of Technology,Guangzhou 510640,China

h i g h l i g h t s

•Global look-up table strategy is used to accelerate B-spline interpolation in digital image correlation(DIC).

•Performance of the strategy is evaluated theoretically and experimentally.

•The strategy is found a superior substitute for the one with bicubic interpolation.

a r t i c l ei n f o

Article history:

Accepted 25 April 2016

Available online 10 May 2016

Digital image correlation

Inverse compositional Gauss-Newton algorithm

Cubic B-spline interpolation

Bicubic interpolation

Global look-up table

Global look-up table strategy proposed recently has been proven to be an efficient method to accelerate the interpolation,which is the most time-consuming part in the iterative sub-pixel digital image correlation(DIC)algorithms.Inthispaper,agloballook-uptablestrategywithcubicB-splineinterpolation is developed for the DIC method based on the inverse compositional Gauss-Newton(IC-GN)algorithm. The performance of this strategy,including accuracy,precision,and computation efficiency,is evaluated through a theoretical and experimental study,using the one with widely employed bicubic interpolation asabenchmark.Thegloballook-uptablestrategywithcubicB-splineinterpolationimprovessignificantly the accuracy of the IC-GN algorithm-based DIC method compared with the one using the bicubic interpolation,at a trivial price of computation efficiency.

©2016 The Authors.Published by Elsevier Ltd on behalf of The Chinese Society of Theoretical and Applied Mechanics.This is an open access article under the CC BY-NC-ND license(http:// creativecommons.org/licenses/by-nc-nd/4.0/).

Digital image correlation(DIC)is a non-contact and full-field optical measurement technique which has found a wide variety of applications[1-5].To achieve high accuracy and precision of measurement,various sub-pixel DIC algorithms have been developed in the past years,among which the one based on the inverse compositional Gauss-Newton(IC-GN)algorithm[6]has become a popular DIC algorithm nowadays due to its superior performance (accuracy,precision,and computation efficiency)[1,7-9].As an iterative optimization algorithm,the performance IC-GN algorithm depends heavily on the interpolation,whereby the intensity map of warped target subset in the deformed image is reconstructed at sub-pixel locations during each iteration step:(i)the bias of interpolation affects directly the accuracy of the sub-pixel DIC algorithms.Researchers studied the influence of various interpolation algorithms on the accuracy of the sub-pixel DIC methods quantitatively[10-14].Their work demonstrates that the cubic B-spline interpolation leads to considerably less bias of the obtained results compared with the bicubic interpolation;(ii)the interpolation is themosttime-consumingpartoftheiterativeprocedure.Recently, Pan and Li[15]proposed a global look-up table strategy to accelerate the bicubic interpolation for the iterative sub-pixel DIC algorithm.By using a pre-computed table of interpolation coefficients, the interpolation times for processing a pair of subsets can be reducedforalmosttwoordersofmagnitude.Thesimilarstrategycan be also employed to alleviate the influence of the non-linear error in processing of digital fringe patterns[16].

In this paper,a global look-up table strategy with cubic B-spline interpolation is developed for the IC-GN algorithm-based DIC method.The developed DIC method is compared with the one using the same strategy but with bicubic interpolation,at the aspects of accuracy,precision and efficiency.

In both cubic B-spline interpolation and bicubic interpolation,a pieceofsmoothsurfaceofintensityisconstructedovereach2X2-pixel grid(qijq(i+1)jqi(j+1)q(i+1)(j+1))in the image,as illustrated in Fig.1.The surface guarantees that it goes through the fourinteger-pixel corners and its first and second partial derivatives are continuous.The intensity t(x,y)at sub-pixel location on this surface can be expressed as a polynomial form

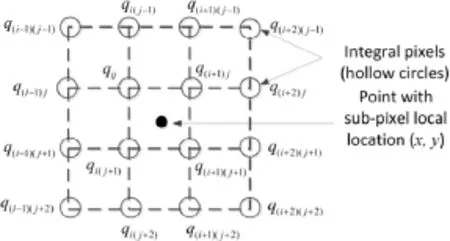
Fig.1.Illustrationof4X4-pixelgridforcalculationof16interpolationcoefficients.

where(x,y)denotesthelocalcoordinatesofthesub-pixellocation with respect to the upper-left corner of a 2X2-pixel grid(Fig.1).is a matrix containing 16 interpolation coefficients

calculated using the intensity informationof a grid of 4X4 integer pixels surrounding this sub-pixel location.

For the cubic B-spline interpolation,the coefficient matrix a of each grid can be calculated according to Ref.[17] where

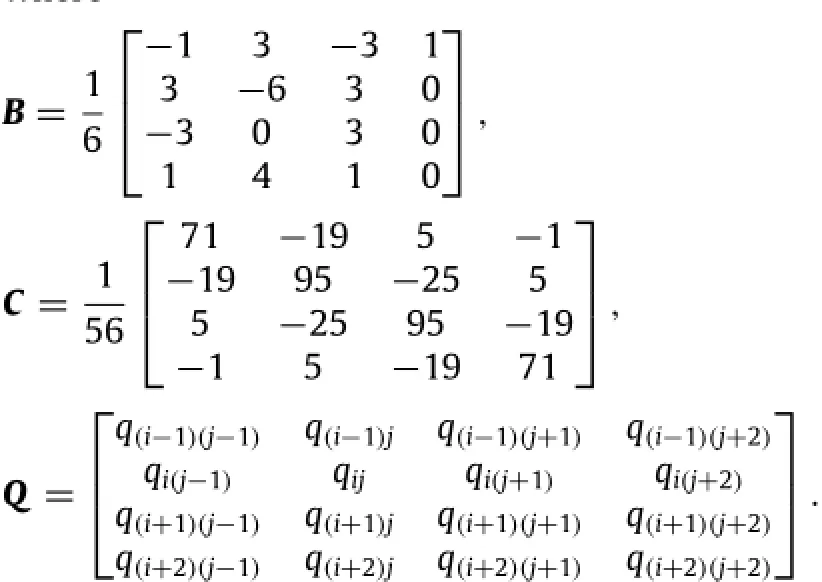
Matrix a has a simple relation with p,i.e.

Forthebicubicinterpolation,theconstructionofcoefficientmatrix a uses not only the intensity at neighboring integer-pixels but also their gradients.A detailed description can be found in Ref.[18].

Agloballook-uptableconsistingof(M-1)X(N-1)elements can be pre-computed on a MXN-pixel speckle image.By repeatedly referring to this table during the iteration,considerable redundant calculations of interpolation coefficients are avoided. Obviously,this is a trade-off between the computation efficiency and memory usage.However,for a 768X576-pixel speckle image the global look-up table requires additional memory of about 56 MB,which could be a trivial expense to current computers.

Table 1 lists the number of operations required to pre-compute matrix a of a 2X2-pixel grid for the two interpolation algorithms. It can be found that the operations for the bicubic interpolation are about 50%less than those for the cubic B-spline interpolation. Moreover,the pre-computation of matrix a for the cubic B-spline interpolation needs an additional transform from matrix p,which leads to extra operations.

The bias raised in the two interpolation algorithms can be compared using the model proposed by Su et al.[14],in which an interpolation bias kernel Eib(vx,vy)is used as an indicator.It is defined as follows,neglecting the aliasing effect along the y-axis

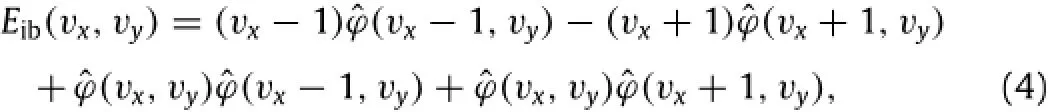
Table 1 Number of operations in cubic B-spline and bicubic interpolation.

wherevxandvyare the frequency of the signals along x-axis and y-axis.Since the lowest period in a digital image is two pixels,the domain ofvxandvyis limited in(-0.5,0.5).ϕˆ(vx,vy) represents the interpolation transfer function,which is the Fourier transform of the convolution kernel of an interpolation function. The interpolation transfer functions of the two interpolation algorithms can be expressed as equations in Box I.

Figure 2(a)and(b)shows the surfaces of Eib(vx,vy)for the cubicB-splineinterpolationandthebicubicinterpolation.Aclearer comparison between the value of the two interpolation bias kernels is performed on the section ofvy=0.1 andvy=0.25, as shown in Fig.2(c)and(d).It can be seen that the value of cubic B-spline interpolation bias kernel is lower than that of bicubic interpolation bias kernel in the low-frequency region(-0.36< vx<0.36).As we know that the energy of an image usually concentrates in the low-frequency region,thus the cubic B-spline interpolation algorithm can reach smaller bias than the bicubic interpolation algorithm for most of speckle images.

Figure3showsapracticalspeckleimagewithasizeof768X576 pixels.Using Fig.3 as the reference image,twenty target images were generated by translating it in Fourier domain according to the shift theorem[10],with pre-set sub-pixel displacements along x-axis from 0 to 1 pixel.The displacement between every two successive images was set to be 0.05 pixels.

The IC-GN algorithm-based DIC method with the two interpolation algorithms was programmed using C++language and run on a desktop computer equipped with AMD FX-4300 CPU(4 cores, 3.8 GHz)and 8.0 GB RAM.The initial guess for the IC-GN algorithm is estimated using the Fourier transform-based cross correlation(FFT-CC)algorithm.Details of this DIC method can be found in Ref.[9].

The bias caused by the two interpolation algorithms is evaluated using the mean bias error of the calculated results, defined as:

where M denotes the number of points of interest(POIs,center of a subset).In this work,a 33X33-pixel subset is employed in the DIC computation and 15264 POIs are set in each speckle image.uiis the calculated displacement at the ith POI,and udis the pre-set displacement.

Figure 4(a)shows the mean bias errors of the calculated displacements.The dependence of mean bias error on the subpixel displacement is in the form of a sinusoidal function,which stems from the interpolation bias,as explained in Refs.[10,14]. Distinct gap can be observed between the two curves of mean bias errors.The magnitude of mean bias errors caused by the cubic B-spline interpolation can be up to 46%lower than those by the bicubic interpolation,indicating a markedly higher accuracy. The gap also shows dependence on sub-pixel displacement.Theabsolute difference between the two curves reaches its peaks at 0.2 and 0.8 pixels,whereas the two curves are in good agreement around 0.5 pixels,as shown in Fig.4(a).Figure 4(b)shows the standard deviation of the calculated displacements.Discernible difference between the two interpolation algorithms appears in the range of the pre-set displacement from 0.3 to 0.7 pixels,which is up to 0.0019 pixels.

Box I.

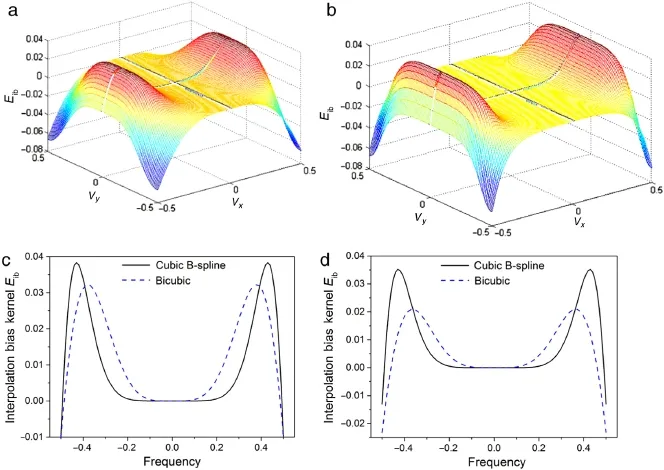
Fig.2.Surfaces of Eib(vx,vy)for(a)cubic B-spline interpolation and(b)bicubic interpolation.The profiles of the two surfaces are compared on the section of(c)vy=0.1 and(d)vy=0.25.

Fig.3.Speckle image used as reference image in experimental study.

Figure 5(a)shows the computation time consumed by precomputation of global look-up tables for the DIC method with the two interpolation algorithms.The pre-computation time taken for the cubic B-spline interpolation algorithm is about 420 ms,almost threetimesasmuchasthatforthebicubicinterpolationalgorithm. However,this discrepancy does not significantly influence the ultimate computation efficiency of the DIC method,because the pre-computation occupies a small share(about 5%-7%)in the overall computation time when processing the speckle image pair with sub-pixel displacement.In Fig.5(b),the average time per iteration of the IC-GN algorithm with the two interpolation algorithms are at same level,with difference less than 1%,as in both interpolation algorithms the intensity at sub-pixel location is obtained according to Eq.(1).It is interesting in Fig.5(c)that the overall computation time consumed by the DIC method with the bicubic interpolation can be remarkably less than that with cubic B-spline interpolation for some sub-pixel displacements, e.g.0.05 pixels and 0.3 pixels.The reason could be attributed to the effects of the interpolation on convergence speed.Figure 5(d) compares the average iteration number in the IC-GN algorithm with the two interpolation algorithms.It can be found that the gap between the two series of data demonstrates similar tendencycompared with that of overall computation time(Fig.5(c)).The bicubic interpolation has larger bias,which generally leads to larger increment of deformation during the iteration,hence the convergence speed.Therefore,in some cases,the IC-GN algorithm with the cubic B-spline interpolation needs one more step to achieve the convergence criterion in comparison with the IC-GN algorithm with the bicubic interpolation.Nevertheless,in most of thecasestheIC-GNalgorithmwiththecubicB-splineinterpolation only increases the computation cost by up to 12%over its bicubic counterpart.

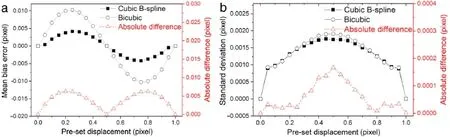
Fig.4.(a)Mean bias errors and(b)standard deviation between the IC-GN algorithm-based DIC method with the two interpolation algorithms.

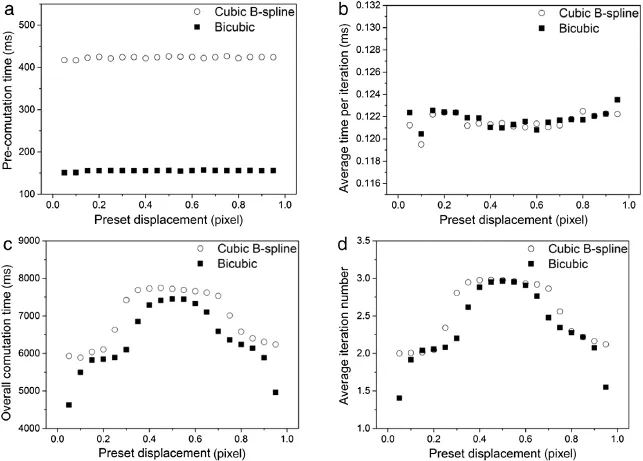
Fig.5.Time consumed by(a)pre-computation of global look-up table,(b)each iteration,and(c)overall procedure of the DIC method.(d)Average iteration number in the DIC method.

This work demonstrates the implementation of global lookup table strategy of cubic B-spline interpolation for the IC-GN algorithm-based DIC method.The theoretical and experimental study is carried out to evaluate the performance of this interpolation strategy in the sub-pixel DIC algorithm,in comparison with the widely used global look-up table strategy of bicubic interpolation.It is found that the IC-GN algorithm-based DIC method can achieve a significantly improved accuracy using the global look-up table strategy of cubic B-spline interpolation,compared with its counterpart with bicubic interpolation.Furthermore,this improvement requires slightly increased computation cost.

Acknowledgments

The work was financially supported by the National Natural ScienceFoundationofChina(11202081,11272124,and11472109) and the State Key Lab of Subtropical Building Science,South China University of Technology(2014ZC17).

References

[1]M.A.Sutton,J.J.Orteu,H.Schreier,Image Correlation for Shape,Motion and Deformation Measurements:Basic Concepts,Theory and Applications, Springer,New York,2009.

[2]B.Pan,Recent progress in digital image correlation,Exp.Mech.51(2011) 1223-1235.

[3]M.A.Sutton,Computer vision-based,noncontacting deformation measurements in mechanics:a generational transformation,Appl.Mech.Rev.65 (2013)050802.

[4]Y.Ma,T.Xiong,X.Yao,Experimental investigation of interface curing stresses between pmma and composite using digital speckle correlation method, Theor.Appl.Mech.Lett.1(2011)51003.

[5]B.Guo,H.Wang,H.Xie,et al.,Elastic constants characterization on graphite at 500°C by the virtual fields method,Theor.Appl.Mech.Lett.4(2014)021010.

[6]S.Baker,I.Matthews,Lucas-Kanade 20 years on:a unifying framework,Int.J. Comput.Vision.56(2004)221-255.

[7]B.Pan,K.Li,W.Tong,Fast,robust and accurate digital image correlation calculation without redundant computations,Exp.Mech.53(2013)1277-1289.

[8]Y.Gao,T.Cheng,Y.Su,et al.,High-efficiency and high-accuracy digital image correlation for three-dimensional measurement,Opt.Laser.Eng.65(2015) 73-80.

[9]Z.Jiang,Q.Kemao,H.Miao,et al.,Path-independent digital image correlation with high accuracy,speed and robustness,Opt.Laser.Eng.65(2015)93-102.

[10]H.W.Schreier,J.R.Braasch,M.A.Sutton,Systematic errors in digital image correlation caused by intensity interpolation,Opt.Eng.39(2000)2915-2921.

[11]Y.Q.Wang,M.A.Sutton,H.A.Bruck,et al.,Quantitative error assessment in pattern matching:effects of intensity pattern noise,interpolation,strain and image contrast on motion measurements,Strain 45(2009)160-178.

[12]L.Luu,Z.Wang,M.Vo,et al.,Accuracy enhancement of digital image correlation with B-spline interpolation,Opt.Lett.36(2011)3070-3072.

[13]Y.Zhou,C.Sun,Y.Song,et al.,Image pre-filtering for measurement error reduction in digital image correlation,Opt.Laser.Eng.65(2015)46-56.

[14]Y.Su,Q.Zhang,Z.Gao,et al.,Fourier-based interpolation bias prediction in digital image correlation,Opt.Express 23(2015)19242-19260.

[15]B.Pan,K.Li,A fast digital image correlation method for deformation measurement,Opt.Laser.Eng.49(2011)841-847.

[16]C.Xiong,J.Yao,J.Chen,et al.,A convenient look-up-table based method for the compensation of non-linear error in digital fringe projection,Theor.Appl. Mech.Lett.6(2016)49-53.

[17]T.Watanabe,Image coding making use of B-spline surfaces,Ieee.T.Circ.Syst. Vid.7(1997)409-413.

[18]http://en.wikipedia.org/wiki/Bicubic_interpolation.

28 January 2016

http://dx.doi.org/10.1016/j.taml.2016.04.003

2095-0349/©2016 The Authors.Published by Elsevier Ltd on behalf of The Chinese Society of Theoretical and Applied Mechanics.This is an open access article under the CC BY-NC-ND license(http://creativecommons.org/licenses/by-nc-nd/4.0/).

∗Corresponding author.

E-mail address:zhenyujiang@scut.edu.cn(Z.Jiang).

*This article belongs to the Solid Mechanics