一种基于变步长差分的电压暂降检测方法

陈鹏伟，李　璐，肖湘宁，陶　顺

(新能源电力系统国家重点实验室(华北电力大学)，北京　102206)



一种基于变步长差分的电压暂降检测方法

陈鹏伟，李璐，肖湘宁，陶顺

(新能源电力系统国家重点实验室(华北电力大学)，北京102206)

电压暂降的实时、准确检测是快速补偿的前提，但频率偏移下基于软件锁相环的检测方法无法准确地检测出相位跳变角。基于αβ-dq变换，提出利用变步长差分来构造出电压的αβ分量，采用恒定50Hz单位正、余弦信号瞬时采样值来构成αβ-dq变换阵，从而计算出电压幅值与相位跳变角，避免了锁相保持给相位跳变角带来的测量误差。并就谐波、噪声及频率偏移等影响因素，对改进方法进行了详细的检测特性分析。理论分析和仿真结果表明，基于变步长差分的改进检测方法，实现方式简单且计算量小，无需同步锁相，可通过调节检测点间隔满足实时性与精确度的不同要求。

电压暂降；变步长差分；αβ-dq变换；频率偏移

0　引　言

随着经济社会的发展和科技的进步，越来越多的非线性、敏感负荷接入电网，使得电网和电力用户因电能质量问题产生巨大的经济损失。其中，电压暂降是引起终端用户电能质量问题的最主要原因之一，指供电电压方均根值在短时间内突然下降至设定阈值以下，经过短暂时间间隔后又回升恢复的现象[1]。可以说，快速、准确地提取出电压暂降特征量，对评估及治理其所引起的电能质量问题，对电能质量相关标准的实施有着重要的意义[2]。

目前，常用的分析方法有方均根值计算法、缺损电压法、基波分量法、小波分析算法、瞬时电压dq分解法及基于dq变换思想的αβ变换法等[3]。其中，由于dq分解法与αβ变换法具有极其良好的动态性能，已成为应用最广泛的实时检测手段。dq分解法能同时检测电压暂降的幅值和相位跳变角，但只适用三相对称扰动，对于单相故障，需要构造虚拟三相电压来实现检测[4-5]。αβ变换法直接将单相瞬时电压从αβ静止坐标系变换到dq旋转坐标系，大大减少了计算量，但不可避免地突出了数据不同时性的问题，即从dq分解的延时60°到延时90°。为了改善这一缺点，文献[6]根据电压波形正弦的特点，提出利用求导的方法构造移相分量，极大地提高了检测的实时特性，但求导构造法对谐波与噪声的放大作用，使得其难以完全满足实际应用的需求。为了降低谐波及噪声对检测结果的影响，文献[7]综合考虑了延时90°法与求导法的优点，采用延时小角度的方法，来构造所需的移相分量。

上述方法中涉及的αβ-dq变换一般都由软件锁相环(SPLL)来实现，为了检测出相位跳变角，需要对同步锁相锁定的相位信息保持一定时间。但随着越来越多的分布式能源接入中、低压网络，系统频率的波动情况逐渐加剧，传统的软件锁相环已不能很好地跟踪电网的频率和相位，测量出的相位跳变角中不可避免地包含频率偏移引起的偏差分量。

针对频率偏移，相位跳变角无法准确测量这一问题，本文在αβ-dq变换检测法的基础上，提出利用变步长差分来构造变换所需的移相量分量，实现简单且计算量小，适用于同步采样。对于αβ-dq变换阵，利用恒定50Hz单位正、余弦信号瞬时采样值来构成，避免锁相保持对相位跳变角的测量误差。并就谐波、噪声及频率偏移等影响因素，详细地分析了所提改进方法的检测特性。理论分析与仿真结果表明，基于变步长差分的改进检测算法，实现方式简单且计算量小，无需同步锁相，对谐波及噪声的放大作用小，并可通过调节检测点间隔，满足实时性与精确度的不同要求。

1　α β变换检测法原理

电压矢量在αβ静止坐标系两个坐标轴上的投影分别为uα=Ucos(ωt+φ)和uβ=Usin(ωt+φ)。dq旋转坐标系相对于静止坐标系以角速度ω旋转，则电压矢量与dq旋转坐标系同步旋转，其在dq旋转坐标系的投影分别为ud=Ucosφ、uq=Usinφ，换到dq坐标系的方法如下：

(1)

式中:αβ-dq变换矩阵元素一般通过软件锁相环获得。

若令uβ分量为实测电压，由uβ分量构造出超前其90°的uα分量，根据式(1)将uα、uβ变换到dq轴上，通过低通滤波获得直流分量ud0与uq0，可得基波电压幅值与相位跳变角：

(2)

(3)

2　改进α β检测法

2.1移相分量构造

基于三点采样，等间隔选取3个采样点，uk-m与uk、uk+m作为前、中、后检测点，可分别表示为

(4)

式中：m为相邻检测点之间的采样间隔点数；Ts为固定采样间隔；ω为实时角速度；相邻检测点之间的相位差可表示为θ=ωmTs，则

(5)

以uk作为uβ，则uα可以表示为

(6)

需要指出，当中间检测点uk为过零点或待观测信号中存在谐波、噪声等扰动分量时，上述方法显然不能适用。理论上，在高频率采样下，当信号能维持在额定频率，检测点间相位差应不变。即使系统发生频率偏移，若采用同步采样，检测点间相位差在同步采样作用下仍可保持近似恒定，则式(6)又可简化为

(7)

式中:h表示相邻检测点之间相位差的正弦值。

2.2α β-dq变换阵构造

αβ-dq变换阵属于旋转变换阵，其中的元素理论上应为待观测电压的相位角变量，一般由软件锁相环SPLL获得。用SPLL获取实时相位角变量是为了获取待观测电压信号的实时相位，从而计算出发生电压暂降时的相位跳变角。但对于相位跳变角的检测而言，并非必须检测出待观测电压信号的实时相位。

实际电力系统运行时的频率一般维持在50±0.5Hz范围内，若直接采用恒定50Hz单位正弦、余弦信号瞬时采样值作为变换阵元素，即

(8)

将uα、uβ代入上式，得

(9)

(10)

式中:Δω=ω-ω0，ω0为额定角速度。则电压幅值与实时相位为

(11)

(12)

可以看出，直接采用恒定50Hz单位正、余弦信号瞬时采样值作为变换矩阵元素不影响电压幅值的检测，但当电压频率偏移50Hz额定值时，就会产生相位量测偏差，对相位跳变角的计算可以通过下式获得

(13)

式中:Δωi为每个采样时刻角速度与ω0的差值;Δω为上个周期电压角速度与ω0的差值;Ts为同步采样间隔。考虑到滤波器的延时作用，n的取值应大于2m，对于巴特沃斯二阶低通滤波器，一般取一个周波的采样点数即可。

3　检测特性分析

3.1谐波影响

考虑待观测信号含有各次谐波分量，3个检测点的采样值可表示为

(14)

根据式(7)，构造出uα，令uβ=uk，代入式(8)，得到ud,uq为

ud=Umcos(Δωt+φ)+

(15)

uq=Umsin(Δωt+φ)+

(16)

电压基波在运算结果中表现为直流分量，第k次高频振荡信号则分解为kω±ω0次高频振荡信号的叠加。与延时90°构造法相比，改进方法对谐波分量有放大作用，并随着间隔角θ的变化而有所不同，具体如图1所示，图中K为谐波放大倍数。

对于不同频次的谐波，选择合适的间隔角θ，可以减小对相应谐波的放大，甚至可以起到抑制谐波的作用。

3.2噪声影响

考虑采样信号中高斯白噪声所带来的影响，对于变步长差分法构造的移相分量而言

(17)

式中:n(t+mTs)与n(t-mTs)分别为t±mTs时刻的噪声分量；Δn(t)为uα中所含的高斯白噪声分量。由于白噪声具有前后时刻的独立性，则在变步长差分法构造的uα中，所含高斯白噪声功率为原始信号的kt=1/(2sin2θ)倍。需要指出，延时δ角构造法对噪声功率的放大作用为kδ=cot2δ+csc2δ倍；求导法对噪声的功率放大为kd=1/(2ωts)2倍；延时90°构造法对高斯白噪声不存在放大作用。

取δ=2θ,fs=12.8kHz，即延时δ角构造法与变步长差分法具有相同延时2mTs的情况下，在θ∈(0,π/2)内，上述各uα构造方法对噪声功率放大系数随θ变化情况如图2所示。

图2　不同检测点间隔角θ对噪声功率的放大比较

由图2可以看出，对于uα，变步长差分法与延时δ角构造法在θ∈(0,π/4)内具有近乎相同的噪声功率放大倍数，且均小于求导法，而大于延时90°法。

3.3频率偏移影响

(18)

式中：Δω21=ω2-ω1，ω2为当前待测电压角速度，ω1同步采样跟踪并保持的角速度，θ=mω1Ts，为恒定值。

(19)

(20)

式中：Δω20表示ω2-ω0，ω20表示ω2+ω0， ΔU为Ucotθsin (mΔω21Ts)/2。当频率偏移时，ud与uq内含有接近100Hz的低幅值振荡分量，需通过适当降低低通滤波器截止频率(100Hz以下)予以滤除，则幅值与实时相位角检测结果分别为

(21)

(22)

若对待观测信号进行高频率采样，在检测装置频率偏移检测要求范围42.5Hz～57.5Hz内，都可以保证ΔU为一极小值。因而可以认为U′=U，φ′=Δω20t+φ。

上述分析仍属于ω2下的极短时稳态分析，对于ω1到ω2的过渡阶段而言，难以用解析法表述其中复杂的暂态特性，但利用前、后检测点来构造中间检测点移相分量的变步长差分法，比延时δ角法更适用于频率偏移的情况。

4　仿真验证

首先，在Matlab/Simulink下，针对220V线路单相接地故障，通过构造不同的电压暂降波形，探究谐波、高斯白噪声、频率偏移对变步长差分检测提取结果的影响，并与基于软件锁相的求导法、延时90°法、延时δ角法的提取结果进行比较。然后，用 110kV线路实际单相电压暂降故障波形进行实际检测特性验证。

本文中，若无特殊说明，无频率偏移情况下，所有仿真的采样频率均为12.8kHz，为A相接地故障，电压暂降起始与结束时刻为0.05s与0.12s，滤波器选用2阶巴特沃斯低通滤波器，截止频率设定为100Hz。由于延时δ角法同样具有延时角参数可调的特性，为了更好地比较变步长差分法与延时δ角法的检测特性，特别地取δ=2θ,即延时δ角构造法与变步长差分法具有相同固有延时2mTs，取m=8。

4.1无畸变情况

无畸变情况是指电压角频率维持于50Hz，不受谐波、噪声及频率偏移影响。主要用于验证在理想待测波形下所提方法的可行性，并与求导法、延时90°法、延时δ角法的检测结果进行对比。

图3为应用本文变步长差分法、求导法、延时δ角法及延时90°法获得的暂降检测结果。

图3　ΔU=50%时幅值与相位跳变角检测结果

由图3的检测结果，可以得到如下结论：

① 电压暂降检测存在延时，主要包含检测方法固有延时与滤波器延时两部分，其中滤波器的延时大于检测方法固有延时。

② 在不考滤波器延时的前提下，求导法能几乎(仅2个采样间隔延时)无延时地响应电压的变化；变步长差分法与延时δ角法有近乎一致的响应特性，二者在实时性上均慢于求导法而快于延时90°法。

③ 若暂降前锁相并在暂降期间保持，基于软件锁相技术的求导法、延时90°法与延时δ角法可将相位跳变检测结果保持至暂降结束，而基于非锁相的变步长差分法仅能在暂降/升后保持一个周波的相位跳变角检测结果，有效值区域为两个反向脉冲/凸起间的平滑区域。

④ 变步长差分法在暂降过渡中存在过冲现象，但过冲程度小于求导法，而略大于延时δ角法，可以通过改变间隔角θ予以减小。

4.2含谐波情况

系统发生电压暂降时，往往伴有一定谐波分量，为验证谐波分量对检测结果的影响，在理想220V电压波形上叠加5%的7次谐波与2.5%的11次谐波。图4为ΔU=50%，应用变步长差分法、求导法、延时δ角法及延时90°法获得的暂降检测结果。

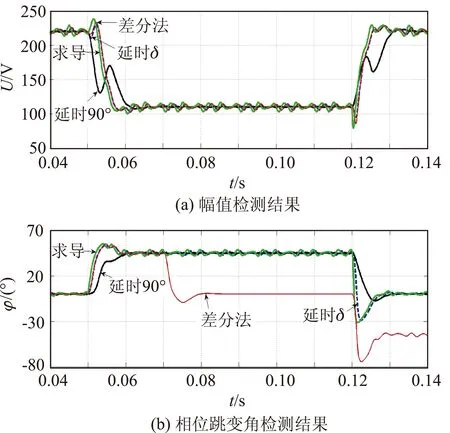
图4　取δ=2、θ=22.5°时含谐波情况幅值与相位跳变角检测结果

由图4可以看出，变步长差分法对谐波存在放大作用，但其放大作用小于求导法，而与延时δ角法近似，可以通过调节间隔角参数减小对谐波的放大作用。

为进一步验证变步长差分法m参数的选取对谐波可能存在的抑制作用，取不同的m值进行检测，并与延时90°法的幅值检测结果进行比较，表1为变步长差分法与延时90°法在0.07～0.11s间幅值检测结果方差值。

由表1可以看出，当m取19或20时，对谐波分量有一定的抑制作用。

表1　0.07～0.11s内幅值检测结果方差

4.3含噪声情况

为了直观地比较4种提取方法在噪声下的检测特性，叠加15dB的高斯白噪声，结果如图5所示，实际检测装置信噪比远大于该值。

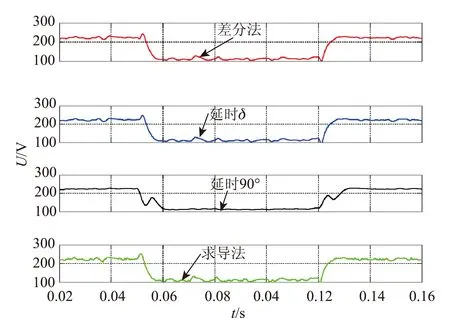
图5　含15dB噪声情况幅值检测结果

由图5可以看出，若以延时90°法的检测结果为参考标准，变步长差分法与延时δ角法会对噪声有近乎相同的放大作用，但该放大作用要小于求导法，与理论分析结果一致。

4.4频率偏移情况

频率偏移发生于0.03s时刻，由初始额定频率50Hz逐渐增加，在0.11s时达到50.5Hz，同步采样频率的跟踪延时设定为一个整周波。电压暂降发生于0.05s，相位跳变角为30°，暂降深度为ΔU=50%。图6为该情况下应用本文变步长差分法、求导法、延时δ角法及延时90°法获得的相位跳变角检测结果，幅值检测结果与图3类似。

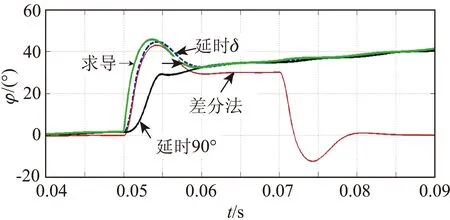
图6　频率偏移情况下暂降电压波形相位跳变角检测结果

结论如下：

①待观测电压信号发生频率偏移时，对幅值的检测不会产生影响。

②由于锁相的相位保持及滤波延时作用，虽然角频率出现较小偏移，仍会使得相位跳变角的检测产生不可忽视的误差，而采用非锁相变步长差分法，可以进行相角偏移补偿，能够有效地减小甚至避免该误差。

4.5实际检测验证

由于检测装置的限制，实际暂降波形为非同步采样，采样频率为25.6kHz，角速度偏差量由过零点时刻计算出来，电压暂降发生于-0.013s时刻，持续时间0.080 24s，检测结果如图7。

图7　实际情况下原始暂降电压波形、幅值与相位跳变角检测结果

由图7可以看出，实际电压暂降过程中，常常伴有谐波与频率偏移，软件锁相会给相位跳变角的检测带来误差而对幅值检测无影响。因此，仅就相位跳变角而言，基于非锁相的变步长差分法消除了频率偏移引起的偏差分量，更适合用于电压暂降特征量的检测。

5　结　论

本文提出了一种基于变步长差分的电压暂降检测方法，并就谐波、噪声、频率偏移对其检测特性的影响做出了详细分析。所提的改进算法与αβ检测法及其他改进算法相比，具有以下特点：

①通过三点检测，即可简单地由差分构造出αβ两相正交分量，方法适用于频率偏移工况；

②无需软件锁相环，仅通过恒定50Hz参考信号构造αβ-dq变换阵，可极大地减小频率偏移带来的相位跳变角检测误差；

③根据实际电压信号的畸变情况选择不同的间隔角度，可综合满足实时性与精确度的不同要求。

[1]肖湘宁，陶顺，徐永海，译. 电能质量手册[M]. 北京：中国电力出版社，2010.

[2]肖湘宁.电能质量分析与控制[M].北京：中国电力出版社, 2010.

[3]罗超，陶顺，肖湘宁.dq变换用于电压暂降瞬时检测的合理性分析[J].电工电能新技术，2014，33(1)：66-70.[4]徐永海， 肖湘宁，刘昊. 电压凹陷特征量检测算法研究[J]. 电力自动化设备，2002，22(1)：19-22.

[5]杨淑英，杜彬. 基于dq变换的动态电压恢复器综合求导检测算法[J]. 电力系统自动化，2008，32(2)：40-44.

[6]张庆超, 肖玉龙. 一种改进的电压暂降检测方法[J]. 电工技术学报, 2006, 21(2): 123-126.

[7]瞿硕，黄纯，江亚群，等. DVR电压暂降检测新方法[J]. 电工技术学报,2013，28(4)：234-239.

(责任编辑：杨秋霞)

A Voltage Sag Detection Method Based on Variable Step Difference

CHEN Pengwei, LI Lu, XIAO Xiangning，TAO Shun

(State Key Laboratory for Alternate Electrical Power System with Renewable Energy Sources(North China Electric Power University), Beijing 102206, China)

The quick and accurate detection of voltage sag is the premise of fast compensation, but under the condition of frequency offset, the phase jump angle is hard to be detected precisely by the software phase locked loop. Based onαβ-dqtransform, a detection method by utilizing variable-step difference is proposed to generateαβcomponents of voltage in this paper. By using instantaneous sample values of the constant 50Hz sine and cosine signals to formαβ-dqtransform matrix, Voltage amplitude and phase jump angle can be calculated, which avoids the measurement error in phase jump angle caused by phase lock holding. The detecting characteristics for such influence factors as harmonics, noise and frequency offset are analyzed in detail by using modified methods. Theoretical analysis and simulation results show that the improved method based on variable-step difference has such advantages as easy realization mode and less calculation amount, which can meet the requirement of real-time and accuracy by regulating detecting sample interval without needing of synchronous phase clocking.

voltage sag; variable step difference;αβ-dqtransform; frequency offset

1007-2322(2016)03-0076-06

A

TM930.12

2015-05-09

陈鹏伟(1992-)，男，博士研究生，主要研究方向为电能质量，分布式发电与直流微网技术，E-mail：chenpw2014@gmail.com;

李璐(1991-)，女，硕士研究生，主要研究方向为主动配电网可靠性评估，E-mail：lilu_1103@163.com;

肖湘宁(1953-)，男，教授，博士生导师，从事电能质量、现代电力电子技术应用等方面的教学与科研工作，E-mail：xxn@ncepu.edu.cn。