基于二阶锥规划的含DG与EV配电网分布式发电有功协调方法

吴杰康，吴志山，林奕鑫, 颜少伟

(广东工业大学自动化学院，广东广州　510006)



基于二阶锥规划的含DG与EV配电网分布式发电有功协调方法

吴杰康，吴志山，林奕鑫, 颜少伟

(广东工业大学自动化学院，广东广州510006)

0　引　言

为了缓解环境与能源的危机，各国都在研究使用新能源技术，分布式电源(DG)和电动汽车(EV)大量增加对配电网运行效益产生的影响成为国内外研究的热点。

目前已经有很多学者对DG与EV接入配电网所产生的影响分别进行了研究。对分布式电源出力分析时充分考虑了其间歇性与不确定性[1-2]；对分布式电源接入配电网的优化问题主要从网损、电压水平与经济性等方面[3-5]进行考虑分析。对电动汽车的研究大多数单独考虑其接入配电网的影响，比如文献[6]建立的充电站最优选址定容模型以节点电压偏移最小及网损最小为目标函数；文献[7]建立的电动汽车充电站最优规划模型是以总网损费用与总成本之和最小为目标函数。目前也有学者对于在配电网中同时接入分布式电源与电动汽车时的有功协调方法进行了研究，文献[8]构建了以全年总费用最小的含分布式电源与电动汽车的经济调度策略和模型。文献[9]建立了以等效负荷率最大、入网服务成本最低的含分布式电源与电动汽车协调控制的多目标优化模型。文献[10]构建了以多时间尺度的等效负荷波动最小的含分布式电源与电动汽车同调度模型，用来平滑系统负荷波动。以上的文献所构建的有功协调方法并没有同时考虑到分布式电源出力的不确定性与电动汽车充电的随机性。

本文针对分布式电源放电与电动汽车充电等具有不确定性变化的特性，分别建立概率模型。由于分布式电源出力和电动汽车的充电的随机性，分布式电源出力与电动汽车充电功率可能有多种运行状态，本文定义系统运行多状态由分布式电源发电的状态和电动汽车充电的状态组成，在此基础上建立配电网中分布式电源出力和电动汽车充电的协调优化模型，以配电网最优运行效益为目标，即最小化期望的社会成本，包括期望的运行成本与期望的停电损失。对于目标函数的优化计算，采用二阶锥规划算法，并与粒子群算法的计算结果进行比较。以IEEE14节点的配电系统为例，对所研究的模型与算法进行了验证与分析。

1　分布式发电的概率模型

1.1风力发电

1.1.1风速的概率模型

对风力速度概率分布的评估，通常采用两参数威布尔分布模型[11]，其一般的表示形式如下：

(1)

(2)

式中:参数c是尺度参数，反应风力的平均风速，其值比平均风速略高；参数k为威布尔分布的形状参数，放映了该分布的偏斜度，通常其取值为1～3之间。对于不同的参数，风速的概率分布也不同。

1.1.2功率模型

对于风力发电而言，只有当风电机组的风速达到了要求的切入风速时才能工作：当风速低于额定风速值，风电机组的输出功率会随着风速的改变而改变；若风速达到额定值及以上时，风电机组的输出功率将以额定功率值平稳输出；如果风速超出规定的切出速度，为了保障风机的安全，则需要停止发电。故采用分段函数来表示功率输出与风速的关系式较为合适。

利用风速概率密度的威布尔分布，可以抽样出不同状态的风速值。在不同的不确定性风速下，风电机组输出功率与不同状态风速关系可以用如下分段函数表示[11]：

(3)

(4)

(5)

(6)

式中:A、B、C是风力发电机组输出功率表达式的参数，它们都为常数；Pn为风力发电机组发出的额定功率值；vr为风力发电机组的额定风速；vci为风力发电机组要求的切入风速；vco为风力机组要求的切出风速；vw为风力发电机组实际的风速值。

1.2光伏发电

1.2.1光照强度的概率模型

由于太阳光辐射具有随机性，其光照强度可用Beta分布[12]来表示：

(7)

式中：α与β为Beta分布的形状参数;r与rm分别是这段时间内实际的光强和最大的光强。

1.2.2功率模型

光伏发电的输出功率不仅与光照射的强度有关，也与温度等不确定因素有关，其表达式如下：

(8)

式中：T为这一时段光伏阵列表面的实际温度；k是温度系数；PT、rT、TT分别是标准测试环境下的最大输出功率、光照强度与光伏阵列温度。

1.3分布式电源出力的状态概率

分布式电源出力不仅受到能源波动的影响，在运行中还可能受到分布式电源故障的影响。因此，分布式电源的出力水平可当成为分布式能源波动的水平与分布式电源运行状态的联合概率分布。

本文的分布式电源运行状态采用两状态的可靠性模型，则其强迫停运率可表示为

(9)

式中:λ为分布式电源的故障率；μ为分布式电源的修复率。

分布式电源的出力状态概率分布可表示为

(10)

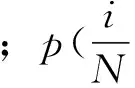
2　电动汽车充电状态的概率分布

随着大量电动汽车投入使用，其充电的不确定性对配电网运行造成一定的影响。下面根据电动汽车充电的不确定因素来建立充电概率模型。本文所讨论的电动汽车充电模式为常规充电，其在电池充满电状态下最大行驶里程D=200 km。

2.1电动汽车日行驶里程与电池余量的概率分布

根据电动汽车日常驾驶数据，可得其日行驶里程概率密度函数[13]：

(11)

式中：标准差μd=3.20;方差δd=0.88，0≤x≤200。

电动汽车每天行驶后电池剩余量SOC与总量的比为

(12)

电动汽车电池余量SOC的概率密度函数：

(13)

电动汽车充电的时长：

(14)

式中:ηEV为电动汽车充电效率;PEV为电动汽车充电功率;W为100km的耗电量。

2.2电动汽车充电状态的概率分布

假设电动汽车在每天结束最后一次出行后进行充电，其常规充电模式开始充电时刻t的概率分布近似为如下的正态分布[14]：

(15)

3　分布式发电协调模型与求解方法

新能源发电、电动汽车充电的不确定性对配电网运行带来一定的影响。为了协调优化新能源发电与电动汽车充电在多种状态下的有功功率，本文以配电网运行经济性期望的运行成本EOC(expected operating cost)和期望的停电损失EIC(expected interruption cost)为目标函数来计算。

3.1协调优化模型

3.1.1系统状态选择

本文定义系统的运行状态空间S由分布式电源发电的状态和电动汽车充电的状态组成，则处于第k个系统状态的概率可表述如下：

(16)

式中：pDG(t)、pEV(t)分别为t时段分布式电源发电状态的概率、电动汽车充电状态的概率。

3.1.2期望运行成本

配电网运行经济性的期望运行成本CEOC主要包括主电网电源期望的发电成本CEOCG、分布式电源期望的运行成本CEOCDG。

① 主电网发电机组的期望发电成本

主电网中传统发电机组的期望发电成本为

(17)

式中：p(xk)为第k个系统状态的概率；PGn(t)为t时刻主网电源n的有功功率；f(PGn(t))为主网电源发电成本函数。

发电成本：

(18)

式中：a、b为电量成本系数。

② 配电网中分布式电源的期望运行成本

配电网中分布式电源的期望运行成本为

(19)

式中：PDGm(t)为t时刻分布式电源m的有功功率；f(PDGm(t))为分布式电源运行成本函数。

由于风电、光伏发电等新能源没有燃料成本，故其运行成本只考虑运行维护成本：

(20)

式中：K为运行维护系数；Δt为运行时间。

3.1.3期望的停电损失

(21)

式中:h(PCi(t))为负荷节点i的停电损失函数；PCi(t)为t时刻母线i的切负荷量；VoLLi为负荷节点i的失负荷价值[15];ND为配网所有节点的集合。

3.1.4目标函数

本文构建的有功协调模型是以配电网运行经济性最优为目的，其目标函数为最小化期望的社会成本，控制变量为主网发电机的有功功率PGi和节点切负荷量PCi：

(22)

3.1.5约束条件

① 系统潮流的约束

(23)

(24)

② 发电机的功率约束：

(25)

③ 节点电压的约束：

(26)

④ 线路电流的约束

(27)

⑤ 切负荷量的约束：

(28)

⑥ 分布式电源容量的约束：

(29)

⑦ 电动汽车充电功率的约束：

(30)

式中：i∈ND，j∈Ω(i);PGi、PDGi、PEVi、PLDi、PCi分别为节点i上主网电源注入的有功功率、DG注入的有功功率、EV注入的有功功率、负荷注入的有功功率、切负荷量；QGi、QDGi、QEVi、QLDi、QCi分别为节点i上主网电源注入的无功功率、DG注入的无功功率、EV注入的无功功率、负荷注入的无功功率、所切负荷的无功功率；Ui，min、Ui，max分别为节点i电压幅值的上下限；Iijmax为流过支路ij最大电流；SDGi，max为节点i接入DG容量的最大值；PEV，max为EV充电功率的最大值。

3.2求解方法

本文所采取的求解方法是二阶锥规划，该算法不仅能求解潮流计算的问题，还能实现优化问题的求解。在优化问题求解中，考虑到潮流约束等式计算的复杂性，本文首先对潮流模型优化，转化成锥优化模型，将潮流变量间复杂的关系以线性公式替代，而新变量间则用特殊结构的锥集表示，从而简化了优化模型。

3.2.1锥优化标准形式

锥优化是线性规划和非线性规划的推广形式[16]，其目标函数必须为线性函数,并且可行域由线性等式或不等式约束与旋转锥或二次锥不等式约束组成，其标准形式如下：

(31)

式中：x为变量，Ki满足旋转锥如下式：

(32)

3.2.2约束条件的锥转化

本文的目标函数为线性函数，满足锥规划形式，故其不需进行锥形式转化，只需对非线性约束条件进行锥形式转化。为了将约束条件中Ui、Uj、θij等乘积的非线性形式转化为满足优化的线性条件的要求，引入了以下变量替换[17]:

(33)

则约束条件相应的变换为

(34)

(35)

采用Mosek数学工具求解计算时，需将式(35)改写为

(36)

分布式电源容量约束条件的锥转化：

(37)

通过变量的替换，式(34)满足锥优化线性约束条件的要求；式(36)、(37)形成了二次旋转锥的笛卡尔乘积形式，搜索空间满足在凸锥的范围之内。通过对优化模型线性化的处理，决策变量的搜索空间满足在凸锥的范围之内，有利于提高计算速度和保证计算结果的最优性。

4　实例计算与分析

4.1实例及其数据

本文以IEEE14节点配电系统为例，其有3条馈线，基准容量为100MVA，基准电压为23kV，总负荷为28.7MW，如图1所示。

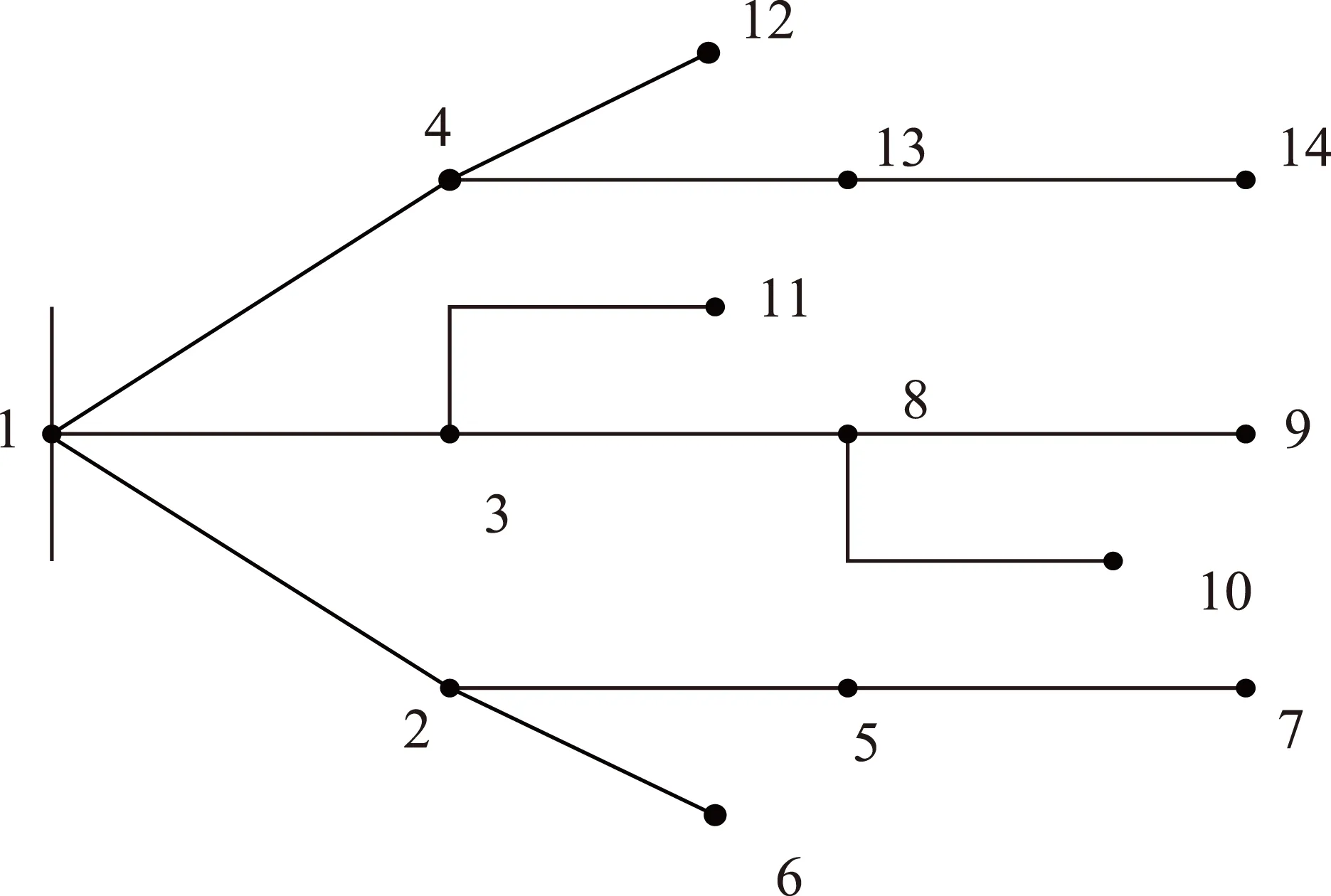
图1　IEEE14配电系统结构图

本文风机采用的数据为切入风速3m/s、切出风速25m/s、额定风速13m/s，额定功率为1MW，强迫停运率为0.05。光伏发电最大辐照度为900W/m2,额定功率为1MW，强迫停运率为0.05。单台电动汽车充电功率为5kW, 充电效率为0.95，100km的耗电量为14 kW。优化调度周期是24h，分为24个时段。

假设主网向节点1注入的功率相当于一台发电机，参数如表1所示[18]。

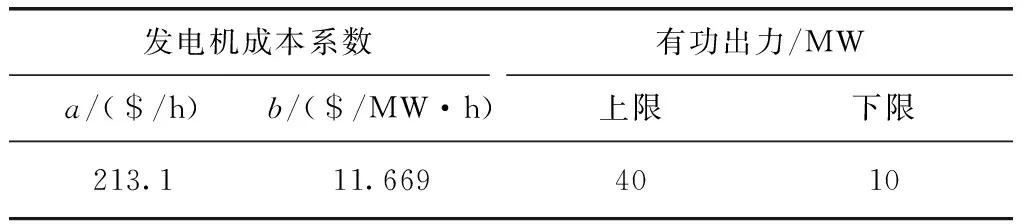
表1　发电机数据

4.2分布式电源发电状态概率计算

4.2.1风力发电状态概率

根据风速的概率模型与输出功率的特性，将风机出力离散化等效为11状态的机组。对一天中任一个时段的风速模拟10 000次，可得风速的概率分布函数(图2)与风电出力样本数目(图3)。

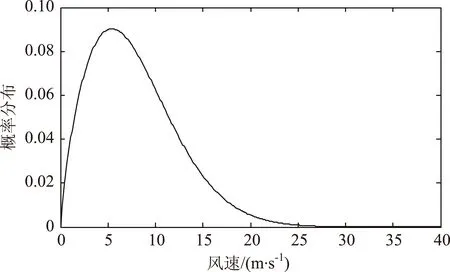
图2　风速的概率分布

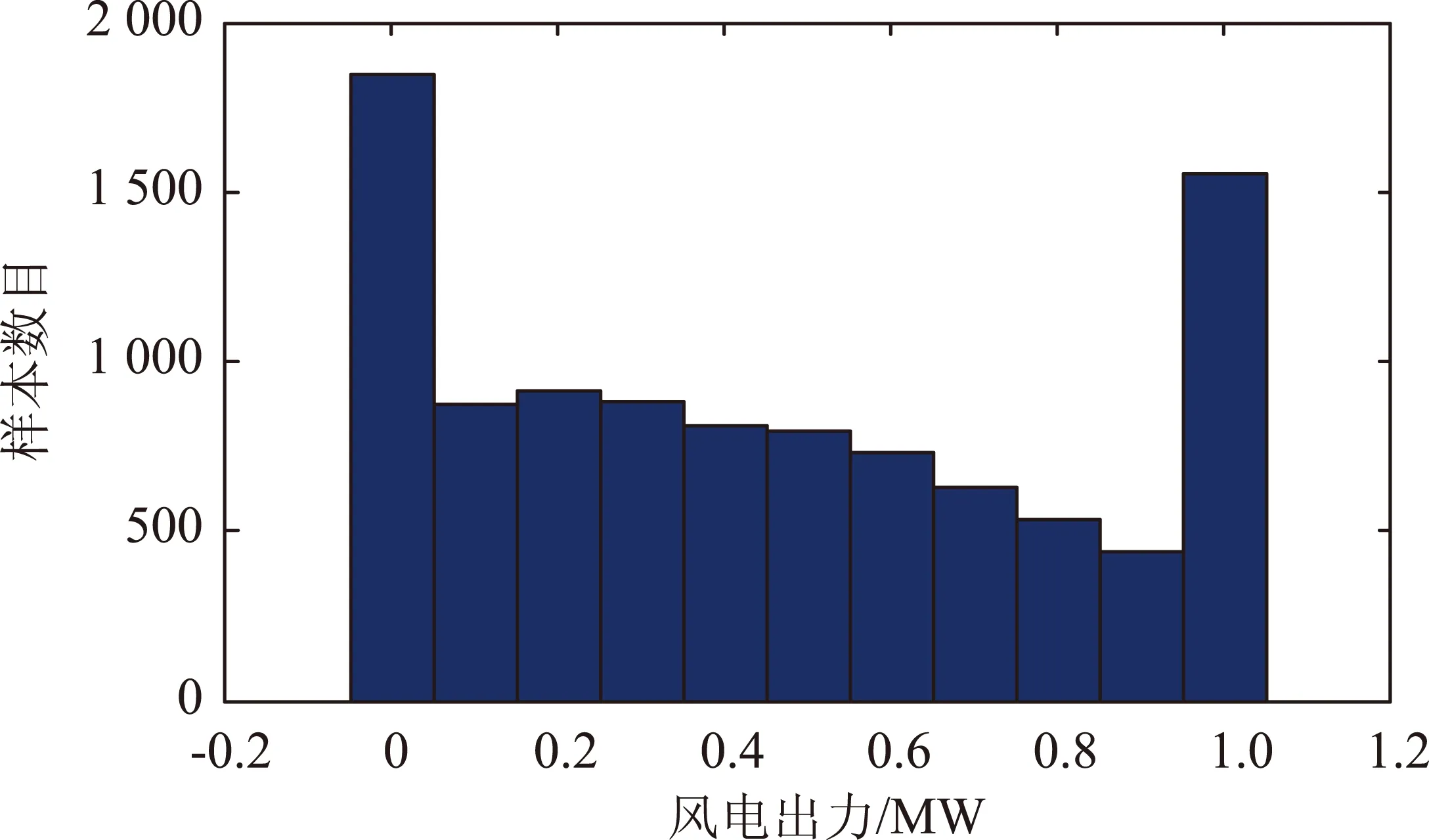
图3　风电出力样本数目

将每一时段风电输出功率分为11种状态，不考虑风机的故障与考虑风机的故障分别对应的出力状态概率如表2所示。

4.2.2光伏发电状态概率

根据式(7)～式(8)，可得某一个时段光伏出力的概率分布，如图4所示。光伏发电出力的状态概率分析与风电类似。

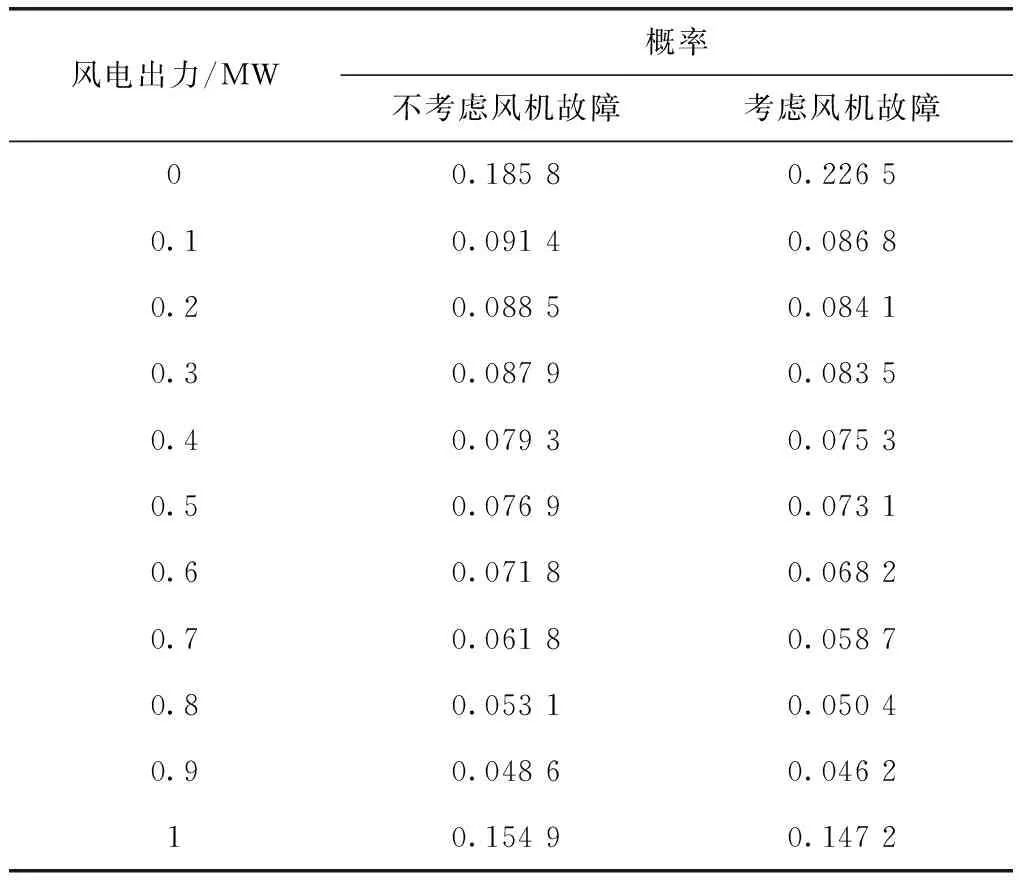
表2　任一个时段风电出力的概率

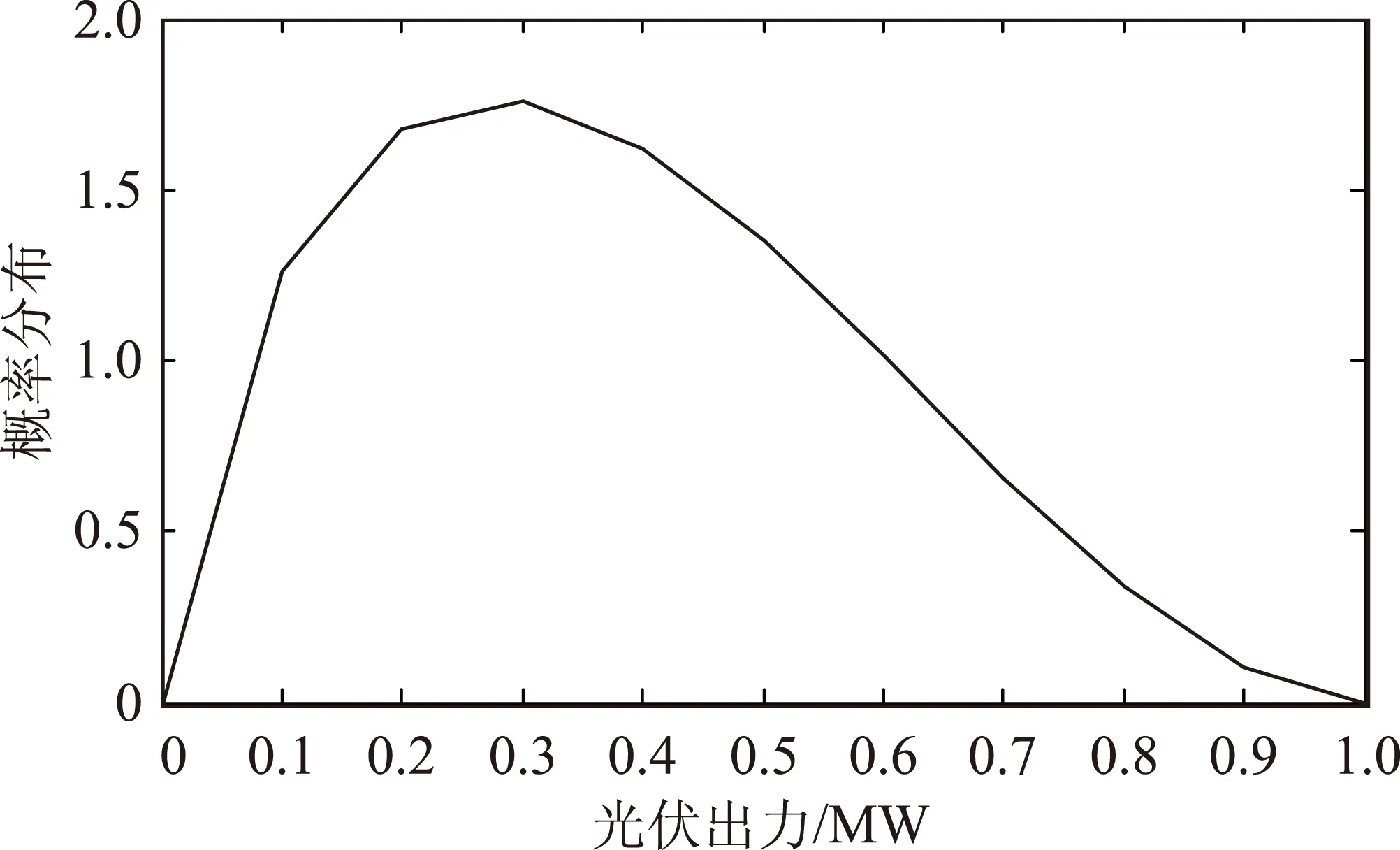
图4　光伏出力的概率分布

4.3电动汽车充电状态概率计算

假设在某一个负荷点接入电动汽车为10 000辆，根据式(9)～式(13)，可得电动汽车开始充电时刻概率分布与充电功率分别如图5和图6所示。

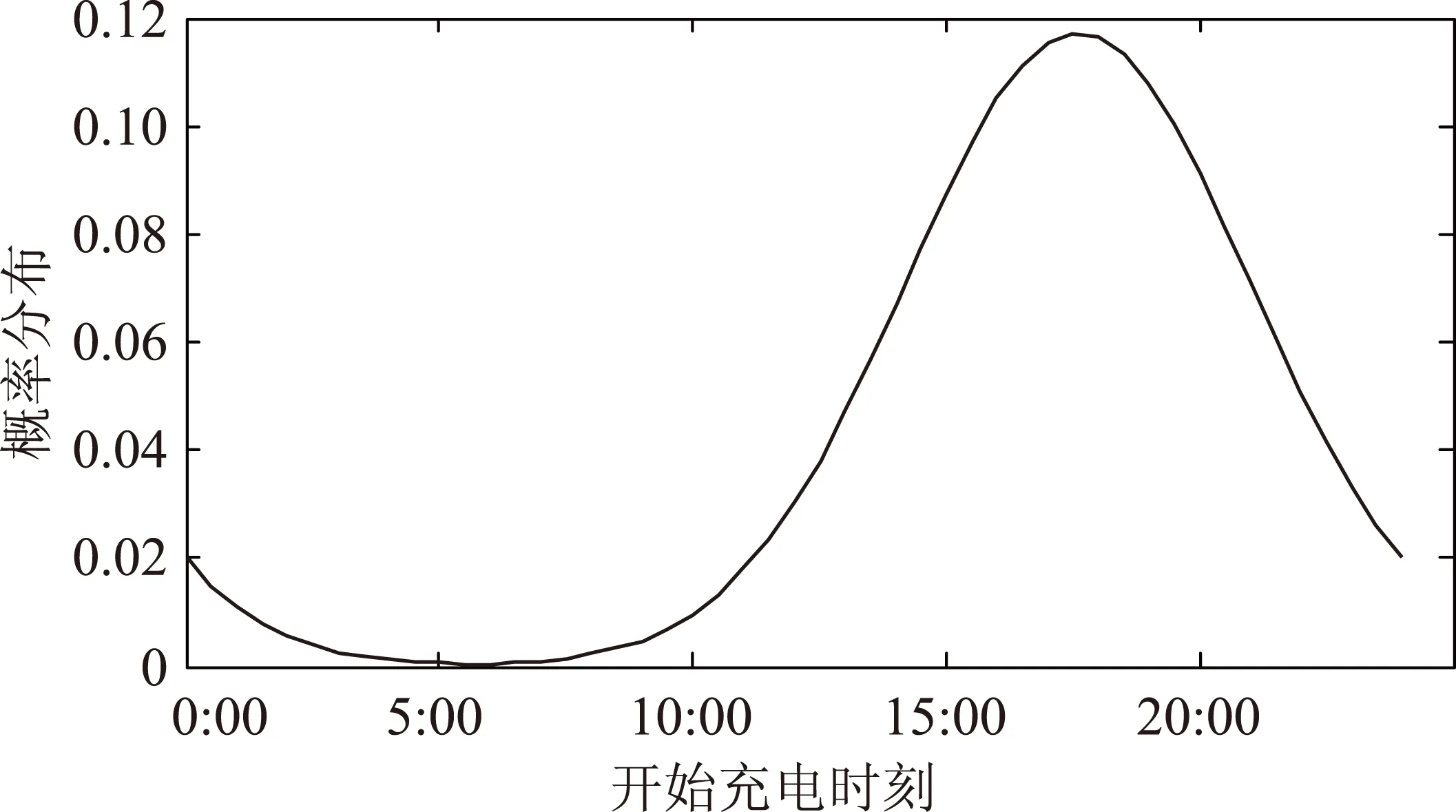
图5　电动汽车开始充电时刻概率分布

对电动汽车在一天里的充电时段分为24个，即有24种状态，其每一时段的平均充电功率对应的概率如表3所示。

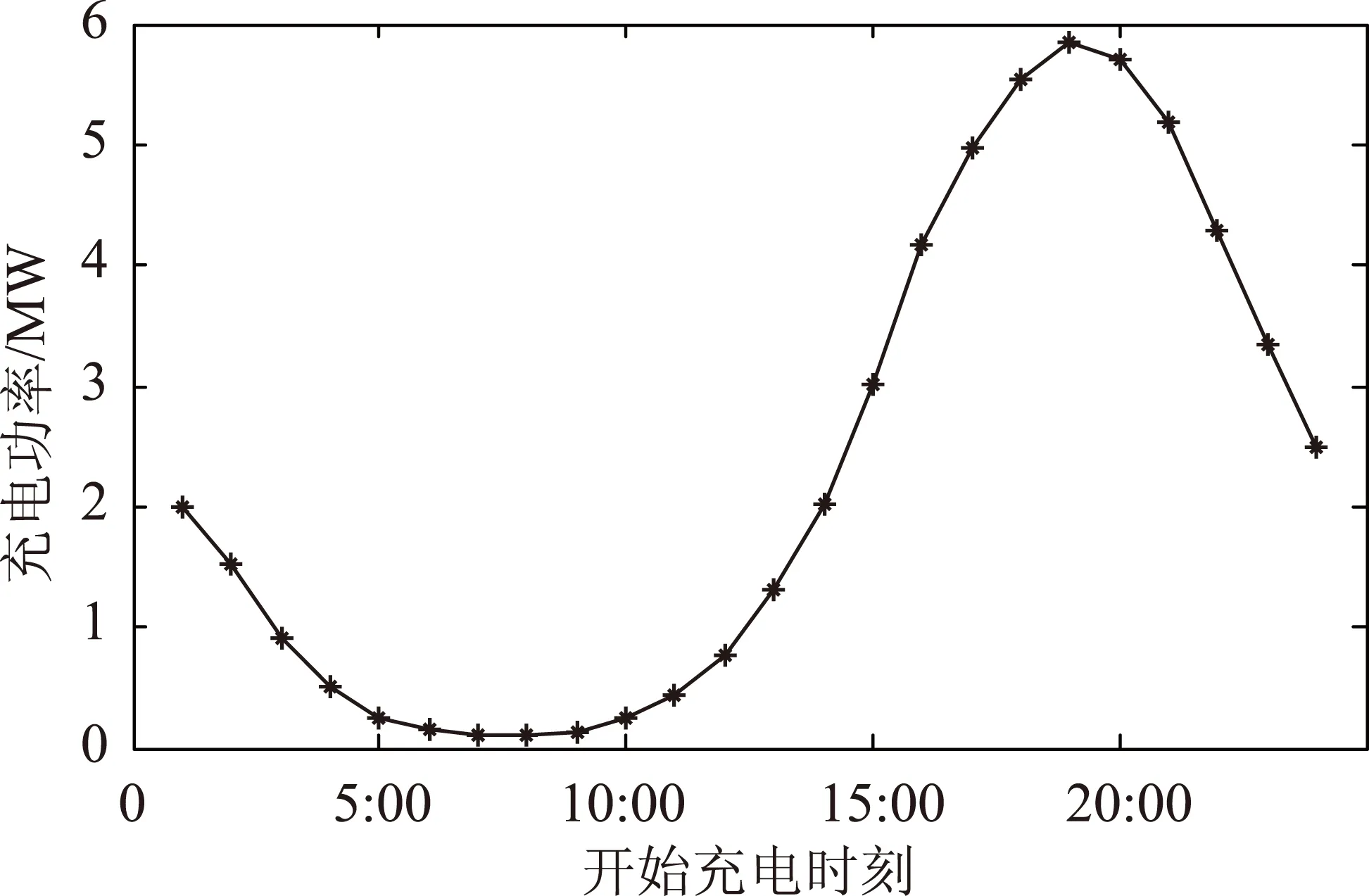
图6　电动汽车充电功率

表3　一天24个时段电动汽车充电的概率

4.4分布式发电与电动汽车充电协调优化计算

为了协调优化计算分布式发电与电动汽车充电在多种运行状态时的有功功率，本文以配电网最优运行经济性来进行优化，即最小化期望的社会成本。下面对两种方案进行优化计算。

方案1：配电网只接入EV，系统有24种状态。本文假设在IEEE14节点配电网的节点7、10、13接入EV。

方案2：配电网同时接入DG与EV,则系统有264种状态。在方案1的基础上，在节点3、4、7、9、10、14接入DG，并分别对不考虑DG故障与考虑DG故障两种情况进行讨论。

对以上方案的优化，采用Mosek数学工具对前面介绍的锥优化算法进行计算，同时与用粒子群算法[19]优化的计算结果进行比较。两种优化算法的计算结果如表4所示，算法进化过程如图7所示。

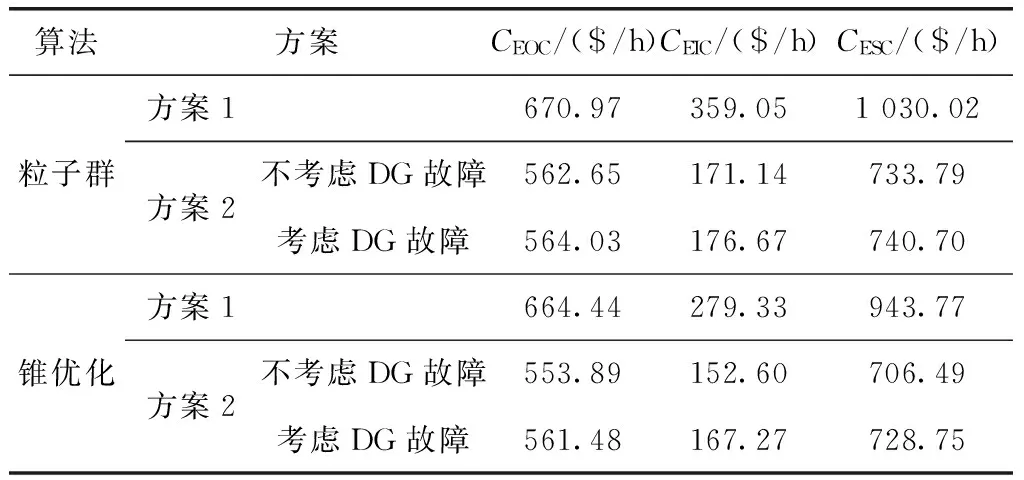
表4　运行成本价值指标

图7　两种算法进化过程曲线

对表4中不同方案下的经济性成本价值指标比较可知，DG与EV同时接入配电网时的期望的运行成本、期望的停电损失与期望的社会成本比只含EV时的小，说明DG接入配电网，通过协调优化分布式发电与电动汽车充电在多种运行状态时的有功功率有利于提高配电网的运行效益。

对表4中方案2不考虑DG故障和考虑DG故障时的指标比较可知，计及DG故障时的运行成本价值指标比不计及DG故障时的略大，可知DG故障降低电网的运行效益， DG运行状态对电网运行成本价值指标有一定的影响，但考虑了DG故障率时的系统运行状态更符合实际情况。

对表4和图7中不同优化算法计算的结果和迭代次数比较可知，本文所采取的二次锥规划计算的运行成本价值指标的值比用粒子群算法计算的值小，且达到最优值时的迭代次数少，收敛速度快，从而证明本文所采取的算法的可行性与优越性。

通过采取二阶锥规划对DG发电与EV充电在多状态运行下的有功协调优化计算，得出配电网最优运行成本价值指标，为电网的调度运行提供可行的参考。

5　结　论

本文考虑了DG(如风电、光伏)输出功率的随机性与EV充电的不确定性，并分别建立其功率的概率模型，计算出某一个时段输出功率/充电功率的状态概率，从而构建系统状态。为了协调优化DG发电与EV充电在多种运行状态下的有功功率，构建的模型为以配电网运行经济性最优为目的，最小化期望的社会成本，包括期望的运行成本和期望的停电损失。通过对实例的讨论分析，可以得出以下的结论：

① 所构建的有功协调模型体现了DG发电与EV充电的不确定性对配电网运行的影响，DG与EV的协调有利于降低配电网运行期望的社会成本，提高电网运行的经济效益。考虑DG故障状态时电网运行经济效益比不考虑DG故障时的有所下降。

② 本文所采用的二阶锥规划方法，能够容易对非线性约束条件进行锥形式处理和转化，简化了本文所提出优化问题的原问题，使求解更快、更稳定，收敛性更好。通过与粒子群算法计算的结果相比，本文提出的二次阶锥规划计算的结果更优，证明了所用算法的有效性与优越性。

③ 在不同状态下，DG发电状态概率与EV充电状态概率完全不同，因此需要进行分布式发电和电动汽车充电在多状态下的有功协调优化，实现主电网发电机组的期望发电成本、配电网中分布式电源的期望运行成本、社会期望停电成本最小化。

[1]WANG J,SHAHIDEHPOUR M. Security-constrained unit commitment with volatile wind power generation[J] .IEEE Transactions on Power Systems， 2008,23(3):1319-1327.

[2]Vlachogiannis, J G. Probabilistic Constrained Load Flow Considering Integration of Wind Power Generation and Electric Vehicles [J].IEEE Transactions on Power Systems， 2009,24(4):1808-1817.

[3]刘波，张焰，杨娜.改进的粒子群优化算法在分布式电源选址和定容中的应用[J].电工技术学报,2008,23(2)：103-108.

[4]刘学平，刘天琪，王剑.基于小生境的配电网多目标分布式电源规划[J].电网技术,2010,34(10)：126-130.

[5]夏澍，周明，李庚银.分布式电源选址定容的多目标优化算法[J].电网技术，2011，35(9)：115-121.

[6]Wang G,Xu Z,Wen F,et al.Traffic-constrained multiobjective planning of electric-vehicle charging stations[J].IEEE Trans. on Power Delivery,2013,28(4)：2363-2372.

[7]刘志鹏，文福拴，薛禹胜，等.电动汽车充电站的最优选址与定容[J].电力系统自动化,2012，36(3)：54-59.

[8]茆美琴, 孙树娟,苏建徽.包含电动汽车的风/光/储微电网经济性分析[J]. 电力系统自动化, 2011，35(14) ：30-35.

[9]李惠玲，白晓昆，谭闻，等.电动汽车与分布式发电入网的协调控制研究[J]. 电网技术, 2013，37(8): 2108-2115.

[10]于大洋，宋曙光，张波，等.区域电网电动汽车充电与风电协同调度的分析[J].电力系统自动化，2011，35(4)：24-29.

[11]Karki R,Patel J. Reliability assessment of a wind power delivery system [J].Proceedings of the Institution of Mechanical Engineers，2009，223(1)：51-58.

[12]Moharil R M,Kulkarni P S. Reliability analysis of solar photovoltaic system using hourly mean solar radiation data [J].Solar Energy，2010，84(4)：691-702.

[13]Kejun Qian,Chengke Zhou,Malcolm Allan,et al. Load Model for Prediction of Electric Vehicle Charging Demand[C]//2010 International Conference on Power System Technology, Hangzhou, China,2010: 1-6.

[14]田立亭，史双龙，贾卓.电动汽车充电功率需求的统计学建模方法[J].电网技术，2010，34(11)：126-130.

[15]TOEFSON G, BILLINTON R, WACKER G, et al. A Canadian customer survey to assess power system reliability worth [J]. IEEE Trans. on Power System. 1991, 9(1):443-450.

[16]Andersen E D, Roos C, Terlaky T. On implement a primal-dual interior point methods for conic quadratic optimization [J]. Mathematical Programming, 2003, 95(2): 249-277.

[17]Jabr R A. Radial distribution load flow using conic programming [J]. IEEE Trans. on Power System,2006,21(3):1458-1459.

[18]孙元章, 程林，何剑.电力系统运行可靠性理论[M].北京:清华大学出版社, 2012.

[19]赵晶晶,李新，彭怡，等. 基于粒子群优化算法的配电网重构和分布式电源注入功率综合优化算法[J]. 电网技术, 2009，33(17): 162-166.

(责任编辑：杨秋霞)

Active Power Coordination Method for Distributed Generation in Distribution Networks with DG and EV Based on Second-order Cone Programming

WU Jiekang, WU Zhishan, LIN Yixin, YAN Shaowei

(School of Automation, Guangdong University of Technology, Guangzhou 510006, China)

分布式电源出力的不确定性与电动汽车充电的随机性给配电网运行效益带来一定的影响。本文根据分布式发电功率和电动汽车充电功率的不确定性，提出了分布式电源出力状态概率模型和电动汽车充电功率状态概率模型，在此基础上形成系统多状态运行空间，建立了含DG和EV配电网分布式发电有功协调模型。以期望的运行成本与期望的停电损失最小为优化目标。利用二阶锥规划，将目标函数和约束条件函数中的非线性形式通过旋转锥转换为线性形式，而新变量间则用特殊结构的锥集表示，从而简化了优化模型。以IEEE14节点的配电系统为例，对所研究的模型与算法进行了验证与分析，获得了较好的效果。

配电网；分布式发电；电动汽车；有功协调；二阶锥规划

The uncertainties in power output of distributed generation (DG) and the randomness of charging power of electric vehicle (EV) bring certain influence on the operation benefit of distribution networks. Based on the uncertainties of distributed generation and the charging power of electric vehicle, the state probability models of the power output for distributed generation and the charging power of electric vehicles are built, based on which the multiple state operation space of system is formed, and an active power coordination model for distributed generation in distribution networks with DE and EV. In addition, the minimization of expected operation cost and expected cost of the power loss are taken as the optimization objectives. By using second- order cone programming, the nonlinear objective function and constraint function are transformed into a linear funtions by rotated cone function. Then, the relationship between new variables is expressed as cone sets with special structure instead, which simplify the optimization model. An IEEE14 distribution system is used as example to verify the adaptability of the proposed model and the feasibility of the proposed method.

distribution network; distributed generation; electric vehicles; active power coordination；second-order cone programming

1007-2322(2016)03-0035-08

A

TM711

广东自然科学基金项目(S2013010012431, 2014A030313509)；广西自然科学基金项目(2011jjA60017)；广东省公益研究与能力建设专项资金项目(2014A010106026)

2015-08-12

吴杰康(1965-)，男，教授，博士生导师，研究方向为电力系统运行与控制，E-mail:wujiekang@163.com；

吴志山(1992-)，男，硕士研究生，研究方向为电力系统运行与控制,E-mail:583684087@qq.com;

林奕鑫(1992-)，男，硕士研究生，研究方向为电力系统运行与控制；

颜少伟(1988-)，男，硕士研究生，研究方向为电力系统运行与控制。