短波固定通信台站装备维修保障能力评估研究

胡明辉，李国军，雷　斌，李高峰，贾昕杰，包　杨

(1.重庆通信学院，重庆　400035； 2.重庆邮电大学，重庆　400065)



短波固定通信台站装备维修保障能力评估研究

胡明辉1，李国军1，雷斌1，李高峰1，贾昕杰1，包杨2

(1.重庆通信学院，重庆400035； 2.重庆邮电大学，重庆400065)

针对短波固定通信台站维修保障力量体系复杂、量化评估难的问题，研究短波固定通信台站装备维修保障能力评估的指标体系，将主元分析与理想点决策方法相结合，建立一种新的维修保障能力多目标评估模型，实验结果表明：该方法结果清晰、易于解释，为构建短波固定通信台站维修保障体系提供辅助决策手段。

层次分析法；主元分析法；理想点法；短波固定通信台站；维修保障能力；评估

本文引用格式：胡明辉，李国军，雷斌，等.短波固定通信台站装备维修保障能力评估研究[J].兵器装备工程学报，2016(8):47-51.

短波通信历来是国家和军队远程通信和机动通信的基本手段。随着我国综合国力的增强及“一带一路”战略的提出，国家利益不断向外扩展，对国家远洋跨海通信能力提出了更高的要求。当前，远洋机动通信手段主要包括卫星通信和短波通信。由于强对抗环境下卫星通信抗毁抗扰能力弱，因此短波通信建设发展成为了我军“走出去”的当务之急。

短波固定通信台站是短波通信系统的主要组成部分。随着通信设备的不断更新，以及网络化程度大幅提升，短波固定通信台站装备的维修保障日益复杂，成为制约其通信保障能力的一个瓶颈。当前，我军固定通信台站主要依靠设备生产厂家组织维修保障，由于这些台站大多涉密程度高，不便于厂家维修人员直接进入工事内进行现地维修，而只能采取返厂维修的方式进行保障，维修周期长达数个月，与我军作战保障需求严重不符。因此，建立完善的基于自身力量的维修保养制度、规范，提升自身维修保障能力显得极其迫切，对当前固定台站的自身维修保障能力做出及时有效的评估和预测也意义重大。当前，关于评估理论方面的研究很多，但对短波固定台站的维修保障能力进行系统的分析评估的相关研究成果较少。

本文通过分析，采用层次分析法建立短波固定台站维修保障能力评估的指标体系，再综合运用主元分析法及理想解点法对其维修保障能力进行评估，并进行实例验证。对分析短波台站维修保障能力，构建短波固定台站运行维修保障体系具有一定借鉴意义。

1　评估指标体系建立

影响维修保障能力的因素众多，建立合理的短波固定台站维修保障能力评估指标体系是对其进行有效的综合评估的前提和关键。短波固定台站因其职能任务需要，大多位于交通不便的山区，且由营连等基层级部队进行日常的业务处理，属于基层级维修机构，故其维修保障能力评估指标有一定特殊性。本文将短波固定台站所有与维修保障相关因素看作一个系统进行综合评估。根据评估指标理论，评估指标体系建立必须满足科学性、可行性、系统性、独立性等原则，具体流程如图1所示。

根据以上原则流程，结合专家的意见及短波台站实际情况，将影响短波固定台站维修保障能力评估的内容分为如下3个方面：维修保障人员、维修保障物资、维修保障管理。由该3个1级指标可细化为10个2级指标、25个3级指标，建立指标体系如图2所示。

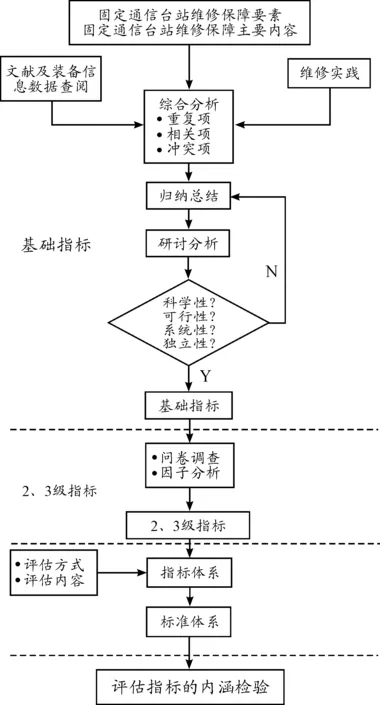
图1　指标体系建立具体流程

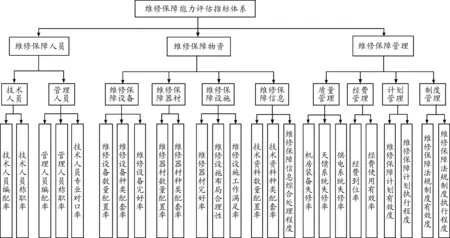
图2　短波固定通信台站维修保障能力评估指标体系

2　基于AHP的指标权重确定

AHP又称层次分析法，是T.L.Satty教授提出的一种定量与定性相结合的系统分析方法，其基本思想是将复杂问题进行层次化，条理化，构造层次分析模型。再按照一定的比例标度，通过两两比较的方式确定各因素的相对重要性，构造上层因素对下层因素的判断矩阵，从而确定各指标相对重要性的总排序。

2.1建立递阶层次结构模型

首先把实际问题条理化、层次化，构造出一个层次分析的结构模型。通常情况下，可分为三层,如图3所示。

图3　递阶的层次结构模型

2.2构造比较判断矩阵

判断矩阵是指人们针对上一层次某因素而言，本层次与之有关的各因素之间相对重要性所做出的判断，判断矩阵的构造是AHP的关键一步。假定A层中因素Ak与下一层中因素B1,B2,…,Bn有联系，则构造的判断矩阵如表1所示。

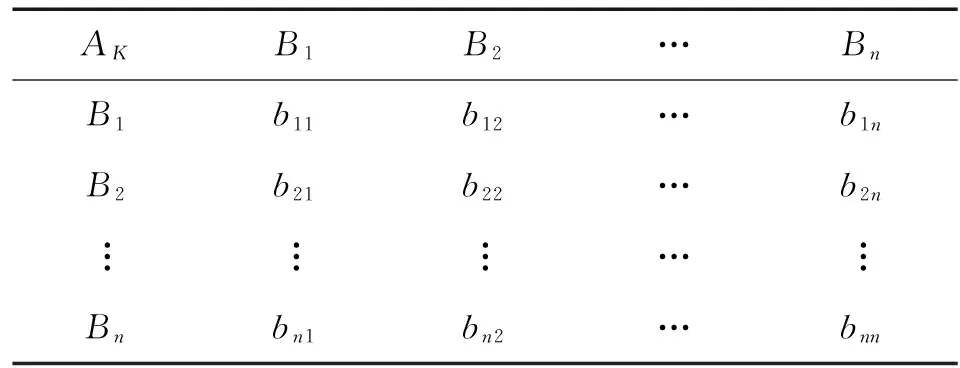
表1　AHP判断矩阵

其中，bij是对于Ak而言，Bi对Bj相对重要性的数值表示，通常bij取1、3、5、7、9及它们的倒数，分别表示Bi与Bj同样重要、稍微重要、明显重要、强烈重要、绝对重要，它们之间的数2,4,6,8及各数的倒数具有相应的类似意义。显然，任何判断矩阵都具有下列性质：

(1)

需要注意的是为避免出现“B1比B2重要，B2比B3重要，同时B3又比B1重要”的矛盾情况，需对判断矩阵进行一致性检验，如果一致性指标不符合标准，需对判断矩阵进行调整。

2.3层次排序

层次排序分为层次单排序和层次总排序。首先进行层次单排序。单排序是指根据判断矩阵计算出对于上一层某因素而言，本层次与之有联系的因素的重要性次序的权值。对判断矩阵B，采用幂法、和积法或方根法计算满足：

(2)

式中：λmax是B的最大特征根，W是对应于λmax的正规化特征向量，W的分量Wi即是相应因素单排序的权值。

表2　层次总排序

3　基于主元分析法与理想点的维修保障能力评估

3.1主成分分析评估方法

设评估站点有m个，每个站点有n个评估指标，则采集矩阵定义为xij(i=1,2,…,m;j=1,2,…,n)。主成分分析利用多元统计分析方法对影响样本指标和各个指标进行分析，通过线性变换将其转换为维数较低的p个互不相关指标变量，亦即主成分变量。主成分分析评估方法的具体步骤如下：

1) 数据标准化

采用Z-Score法对节点指标数据xij进行标准化处理

(6)

其中

从而得到标准化的样本决策矩阵：

2) 指标相关矩阵计算：

(7)

3) 相关矩阵特征分解。计算相关矩阵R的特征值λ1≥λ2≥…≥λn≥0以及相应的特征向量αj=[αj1,αj2, …,αjn]T(j=1,2,…,n)。

4) 主成分决策矩阵。利用上述归一化指标主元αj，可生成主成分：

(8)

选取归一化指标主元的累积能量贡献率满足下式的前p个主成分(通常ε的数值取0.85)：

(9)

由此生成由前p个主成分作为低维指标的主成分决策矩阵F=(zij)m×p=[f1,f2, …，fp]。利用归一化指标主元的方差，可以得到主成分指标权重为

从而可以构造主成分的加权决策矩阵：

(10)

3.2优化决策模型

在现有的主成分评估模型中，大都直接通过主成分的加权平均结果进行决策评估，由于主成分分量通常存在正负数，这种加权决策模型难以给出合理的解释，几何物理意义不明确。为此，本文从空间欧式距离概念出发，利用加权决策矩阵的P个主成分生成P维空间向量，在TOPSIS决策方法框架下，通过欧式距离进行决策判断，以更加充分利用P个主成分信息，且易于给出合理的解释。

TOPSIS法(理想点法)是一种常用的有限方案多目标决策分析法，具有计算简便、结果合理、应用灵活的特点，因此得到了广泛应用。TOPSIS的基本原理是借助于多目标决策问题的“理想解”和“负理想解”进行排序，确定各方案的优劣程度。理想解是一个虚拟的最佳方案，其各个指标值都达到各待评方案中的最优值；负理想解与之恰恰相反，其各个指标值都达到各待评方案中的最劣值。理想解和负理想解分别表示在决策中努力追求和竭力避免的极端情况。具体实现过程如下：

1) 确定理想点。对于主成分加权决策矩阵Z=(zij)m×p，取

从而构造如下正负理想点：

(11)

2) 确定p维空间主成分与理想点的距离:

(12)

3) 计算各采样点主元与理想点主元的相对贴近度。设第i个采样点与理想点主元的相对贴近度为Zi，则:

根据相对贴近度Zi的大小，对各采样点进行排序，Zi越大，表示该采样点离负理想点越远，同时离理想点越近，则该采样点越佳。

4　评估实例分析

根据上述指标体系及评估方法，随机选取15个台站进行评估实例验证。

4.1指标权重确定。

邀请了多名专家，按照层次分析法对上述评估指标体系进行权重打分，得到25个指标最终权重如图4所示。

图4　各项指标最终权重

4.2PCA-TOPSIS评估

在指标权重确定之后，邀请了5位相关领域的专家按照各个指标对各台站进行指标打分，从而得到原始评估样本数据，再根据上述PCA及TOPSIS方法，运用MATLAB进行仿真评估，得到结果如图5所示。

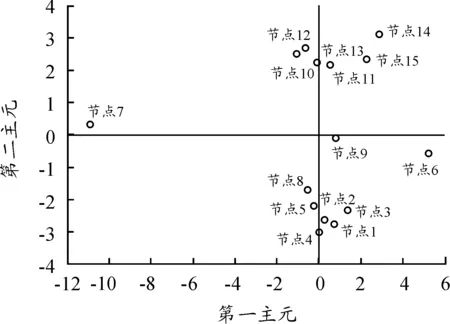
图5　各台站评估结果散点图

上图为以PCA第二主成分对第一主成分的散点图，从图中可以直观看出，从第一主成分的角度看，15个节点大致可以分为3类，节点6最优，节点7最劣，其余节点处于中间位置，相差不多。而从第二主成分的角度看，也可以大致分为3类，其中节点1、2、3、4、5、8得分相近，最优；节点6、7、9处于中间位置；其余节点最劣。如果赋予第一主成分物理意义，比如代表人力因素，则可以通过散点图清楚看到，从人力因素角度，节点6最佳，节点7最劣，其余节点相差不多，人力因素相近。

通过PCA-TOPSIS方法，计算各节点最终综合评估得分，可得图6。

图6　各台站PCA-TOPSIS最终综合得分

由图可以清楚的看到各固定通信台站维修保障能力综合评估结果的大小排序，其中站点6维修保障能力最强，站点7维修保障能力最弱。

4.3与其他方法对比

为验证PCA-TOPSIS方法优势，将该方法与单独用PCA和加权平均法进行了对比。仿真结果对比如图7所示。

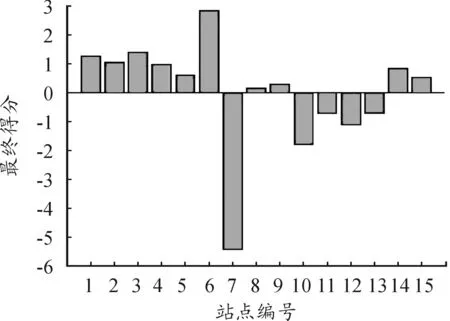
图7　各台站PCA最终综合得分

从图7可以看出，单独采用PCA与采用PCA-TOPSIS方法评估结果一致，均为节点6最佳，节点7最劣。但是，当单独采用PCA时，评估最终得分有正有负，无确切的物理含义，不便于理解。

同时，将PCA-TOPSIS方法与传统的加权平均法进行了对比。通过对实验结果分析，发现因为加权平均法采用相乘再累加的方式计算最终得分，其抗粗差干扰能力较弱，即当某个节点的某个单项指标得分较为突出，而其他指标均较弱时，其最终综合评估结果受大指标的影响较大，易造成评估结果失真。而PCA-TOPSIS抗粗差干扰能力相对较强，评估结果能够更为真实的反映节点综合能力。

5　结束语

本文综合考虑维修保障各个环节，建立了短波固定台站维修保障能力评估的指标体系，利用PCA-TOPSIS方法对维修保障能力进行评估，并通过实例分析，验证了方法的正确性与可行性，对短波固定通信台站维修保障能力评估具有一定的借鉴意义。

[1]李巍峰，王精业.装备保障固有能力评估及评估方法研究[C]//2005年全国仿真技术会议论文集,出版地不详：[出版社不详]，2005:139-141.

[2]张晓南.基于主成分分析的装备综合保障能力评估[J].指挥信息系统与技术，2013,4(5):80-83.

[3]袁义，赵宏宇.BP神经网络在装备维修保障能力评估中的应用[J].电脑与信息技术，2009,17(5)：28-31.

[4]艾宝利，武昌.空军通信装备维修保障系统效能评估体系研究[J].通信导航与指挥自动化，2010(3)：62-65.

[5]高惠璇.应用多元统计分析[M].北京：北京大学出版社，2005.

[6]张福光.基于主成分分析法的军械保障信息化评估方法[J].舰船科学技术,2011(3):45-49.

[7]韩小孩.基于主成分分析的指标权重确定方法[J].四川兵工学报,2012(10):57-61.

[8]杨懿.空军通信装备维修保障系统效能评估研究[D].西安：空军工程大学，2006.

[9]陈光亚.基于主成分分析法的炮兵装备维修保障优化模型[J].四川兵工学报，2014,35(12):88-91.

[10]贾明.基于云AHP模型的保障能力仿真研究[J].系统仿真技术，2014,10(1):64-66.

[11]CHRISTOPHE C,PETER F,HEINRICH F.Robust Sparse Principal Component Analysis[J].Technometrics，2013(2):51-55.

[12]JIA M X,XU H Y,LIU X F,et al.The optimization of the kind and parameters of kernel function in KPCA for process monitoring[J].Computers and Chemical Engineering，2012(5):74-79.

[13]TSAI Y T,WANG K S,TSAI L C.A study of availability-centered preventive maintenance for multi-component systems,2004.

[14]甘茂治，康建设，高崎.军用装备维修工程学[M].北京：国防工业出版社,2005.

[15]裴凤.基于参照点的区间数TOPSIS方法研究[D].合肥:合肥工业大学 2012.

(责任编辑唐定国)

Evaluation of Equipment Maintain Support Capability of HF Fixed Communication Stations Based on PCA and TOPSIS

HU Ming-hui1, LI Guo-jun1, LEI Bin1, LI Gao-feng1, JIA Xin-jie1, BAO Yang2

(1.Chongqing Institute of Communication, Chongqing 400035, China;2.Chongqing University of Posts and Telecommunications, Chongqing 400065, China)

This paper aimed at solving the problem of complex and quantitative assessment of the power system for the maintenance and support of HF fixed communication stations, we established an index system for the evaluation of equipment maintenance support capability of short wave fixed communication station. By combining principal component analysis with ideal point decision method, we established a new multi-objective evaluation model of maintenance support capability. The experimental results show that the method is clear and easy to interpret. It provides a supplementary decision means for constructing the maintenance support system of HF fixed communication stations.

analytic hierarchy process; PCA; TOPSIS; HF fixed communication stations; maintenance support capability; evaluation

2016-02-18；

2016-03-15

国家自然科学基金(61302054)；重庆市基础科学与前沿技术重点项目(cstc2015jcyjBX0078)

胡明辉(1988—)，男，硕士研究生,主要从事战术无线通信与组网技术研究。

李国军，男，副教授，主要从事战术无线通信与组网技术研究。

10.11809/scbgxb2016.08.011

format:HU Ming-hui, LI Guo-jun, LEI Bin, et al.Evaluation of Equipment Maintain Support Capability of HF Fixed Communication Stations Based on PCA and TOPSIS[J].Journal of Ordnance Equipment Engineering,2016(8):47-51.

E962

A

2096-2304(2016)08-0047-05

【后勤保障与装备管理】