带限位的隔离系统抗冲击性能分段建模法研究

厉行军，赵建华，张春辉

(1.东海舰队司令部11分队，浙江 宁波　315000; 2.海军工程大学 动力工程学院，武汉　430033)



带限位的隔离系统抗冲击性能分段建模法研究

厉行军1，赵建华2，张春辉2

(1.东海舰队司令部11分队，浙江 宁波315000; 2.海军工程大学 动力工程学院，武汉430033)

对于采用隔振装置的船舶设备，在遭受外界大冲击时，系统相对位移响应幅值较大，可能会超过设备外接管系的变形范围，甚至超过设备本身的变形能力；因此，在设备保证加速度响应幅值处于设备承受范围的要求下，需在隔振装置中安装合适的限位器用于抑制系统的相对位移幅值；以单自由度单层隔冲系统为研究对象,基于杜哈梅积分，采用分段建模，分析了系统有、无限位器的冲击响应和限位器的主要参数变化对系统抗冲击性能的影响，所得结论可用于指导限位器的设计。

限位器；刚度；间隙；抗冲击性能

本文引用格式：厉行军，赵建华，张春辉.带限位的隔离系统抗冲击性能分段建模法研究[J].兵器装备工程学报，2016(8):29-32.

船舶和船舶设备在服役期间通常会遭受冲击，因此大多数船舶设备在设计时就采用了隔振装置[1-2]。通常隔振器的固有频率较低，因而具有较小的加速度响应幅值[3]，但同时产生的相对位移响应幅值却较大，大大超过了设备外接管系的变形能力，甚至超过了隔振器本身的极限变形能力[4-5]。因此在隔振装置设计过程中，如何防止设备的相对位移幅值超过允许范围非常重要。在设备上安装限位器限制设备的位移，是行之有效的方法之一[6-10]。

实际应用的限位器通常可对系统进行三方向限位，多自由度隔振抗冲系统对冲击激励的瞬态响应，可以采用振型叠加法求解，即通过振型叠加法可以把多自由度系统的冲击问题简化为多个单自由度系统的冲击进行分析和计算[7]。本文主要针对单自由度冲击隔离系统的限位器进行研究，探讨限位器的主要参数对系统在冲击作用下的相对位移响应幅值和绝对加速度幅值的影响。

1　运动方程

由于冲击时间很短，选不考虑阻尼作用的弹性限位器为研究对象，单自由度隔振抗冲系统如图1所示。运动方程：

(1)

式(1)中，m为设备质量，k1为单层隔振器的支撑刚度，k2是限位器刚度，Δx是限位器与设备之间的间隙，x1为基座位移，x3为设备绝对位移。

半正弦波冲击信号：

(2)

式(2)中，A为冲击载荷幅值，ω0为半正弦冲击的圆周频率，t0为冲击持续时间。

图1　带限位器的单自由度隔振抗冲模型

2　系统响应分析

2.1杜哈梅尔积分

对于单质量弹簧系统，单位脉冲发生在t=τ，引起的冲击响应h(t-τ)为

(3)

强度面积为F(τ)Δτ的典型脉冲下，系统的响应可看作每个脉冲引起的响应的总和：

(4)

Δτ趋近于零时，求和变成卷积：

(5)

阶跃函数表示成一系列脉冲函数，得到绝对位移的阶跃响应为

(6)

式(6)称为杜哈梅尔积分。

2.2应用杜哈梅尔积分求解方程

对于图1所示的单自由度隔振抗冲模型，应用杜哈梅尔积分求解系统相对位移响应：

1) 冲击载荷作用阶段，且未接触限位器。设备相对位移y的方程为

(7)

式(7)中，ωn为设备接触限位器前的固有频率。

2) 冲击载荷作用阶段，且接触限位器后。设系统接触限位器后的固有频率为ω2，则设备相对位移为

(8)

式(8)中，t1为设备接触限位器的时刻，y1、v1分别为t1时刻的相对位移和相对速度。

3) 冲击载荷作用结束，且接触限位器前的自由振动阶段。设备相对位移为

(9)

式(9)中，y2、v2分别为载荷作用结束时刻t0的相对位移和相对速度速度。

4) 冲击载荷作用结束，且接触限位器阶段

(10)

式(10)中，y3、v3分别为载荷作用结束时刻t0的相对位移和相对速度。

3　冲击响应计算及分析

通过杜哈梅积分法计算获得式(1)运动方程的相对位移分段计算模型，利用Matlab编程，用于冲击响应计算。

取m=750 kg，k1=4 000 000 N·m，设系统遭受幅值为30 g，持续为10 ms的半正弦冲击，计算了在不同限位器刚度k2=k1～9k1，不同限位器安装间隙Δx=1～7 mm时的冲击响应，分析限位器刚度和安装间隙对冲击响应的影响。

3.1系统无限位器和有限位器时的冲击响应分析

系统无限位器和有限位器(Δx=2 mm,k2=5k1)时的相对位移响应和绝对加速度响应曲线分别如图2和图3所示。从图3中可以看出，在设备添加限位器的一侧，相对位移明显下降，当设备接触到限位器的瞬间，加速度产生突变(增大)，当离开限位器的同时也产生突变(减小)。由于系统无阻尼，故系统将不会有能量耗散，所以不管是在有限位器还是无限位器的情况下，系统的振动响应都是等振幅的响应。

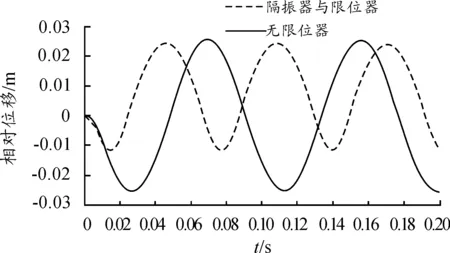
图2　Δx=2 mm, k2=5k1时的相对位移响应

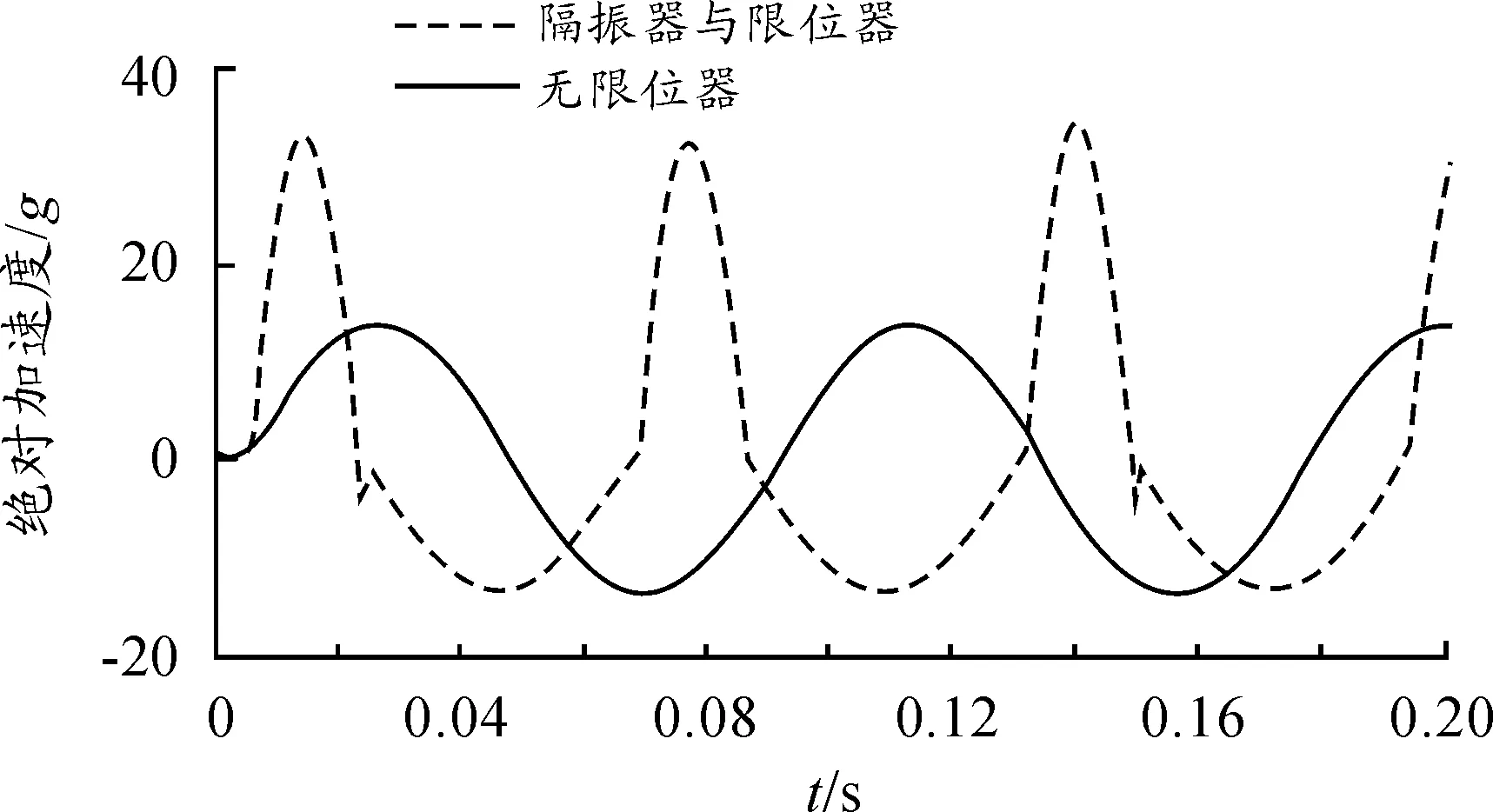
图3　Δx=2 mm, k2=5k1时的绝对加速度响应

3.2限位器安装间隙对系统响应的影响

刚度不变，取限位器安装间隙为1mm、3mm、5mm、7mm，研究限位器安装间隙对系统响应幅值的影响。不同限位器安装间隙下，系统的相对位移响应曲线如图4所示，相对位移幅值随限位器间隙的变化曲线如图5所示。从图5可以看出，相对位移幅值随着限位器间隙的增大而增大，二者近似成线性关系，而且，安装间隙越大，系统达到相对位移幅值所用的时间越长。

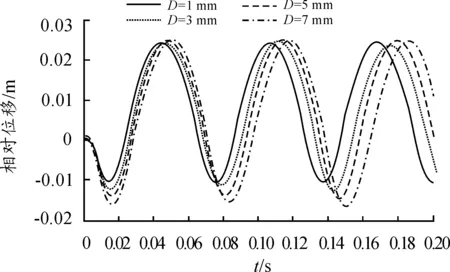
图4　不同安装间隙下相对位移的响应曲线

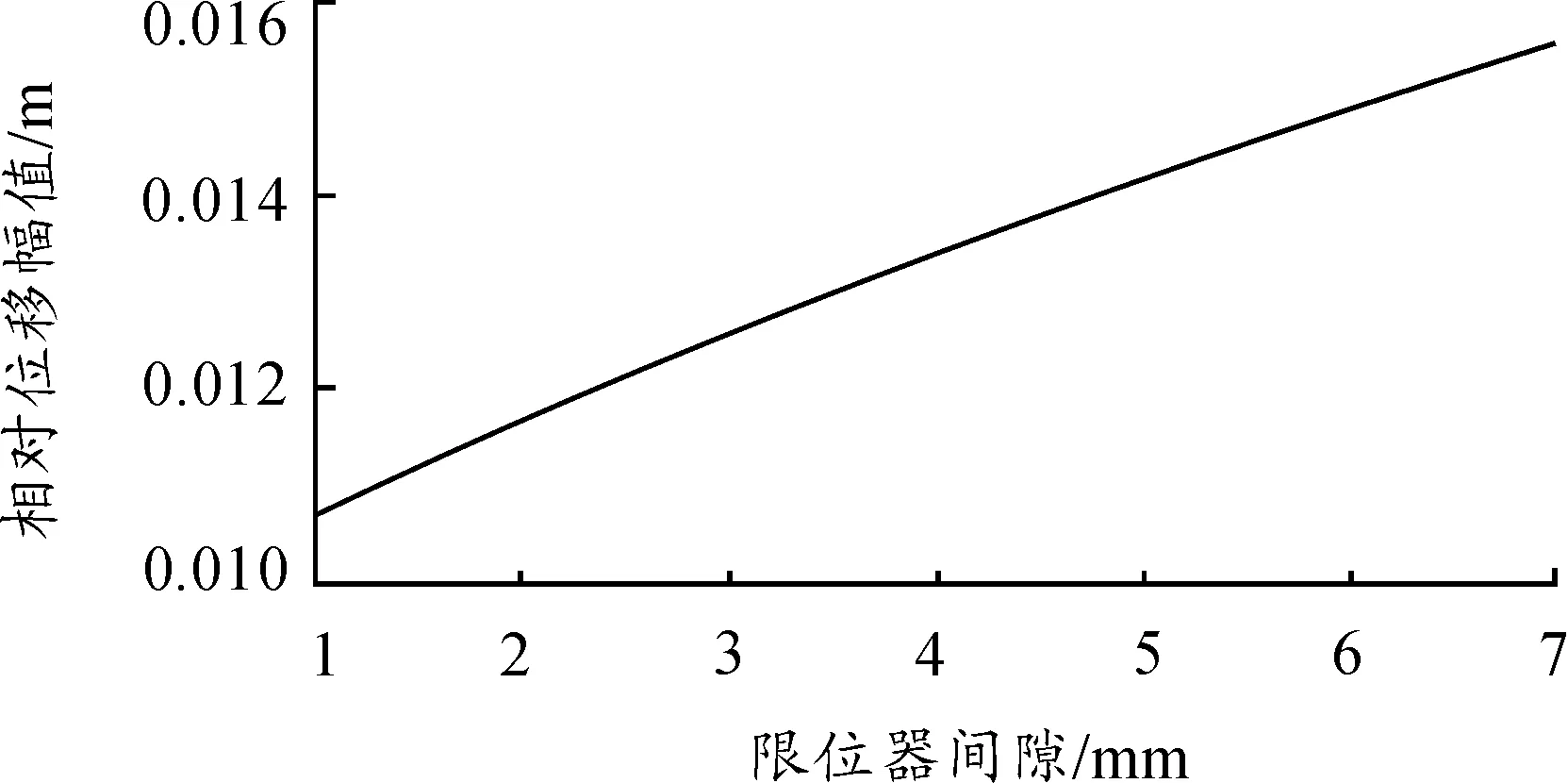
图5　相对位移幅值随限位器间隙的变化曲线

不同安装间隙下绝对加速度响应曲线，如图6所示。绝对加速度幅值随限位器间隙的变化曲线如图7所示。

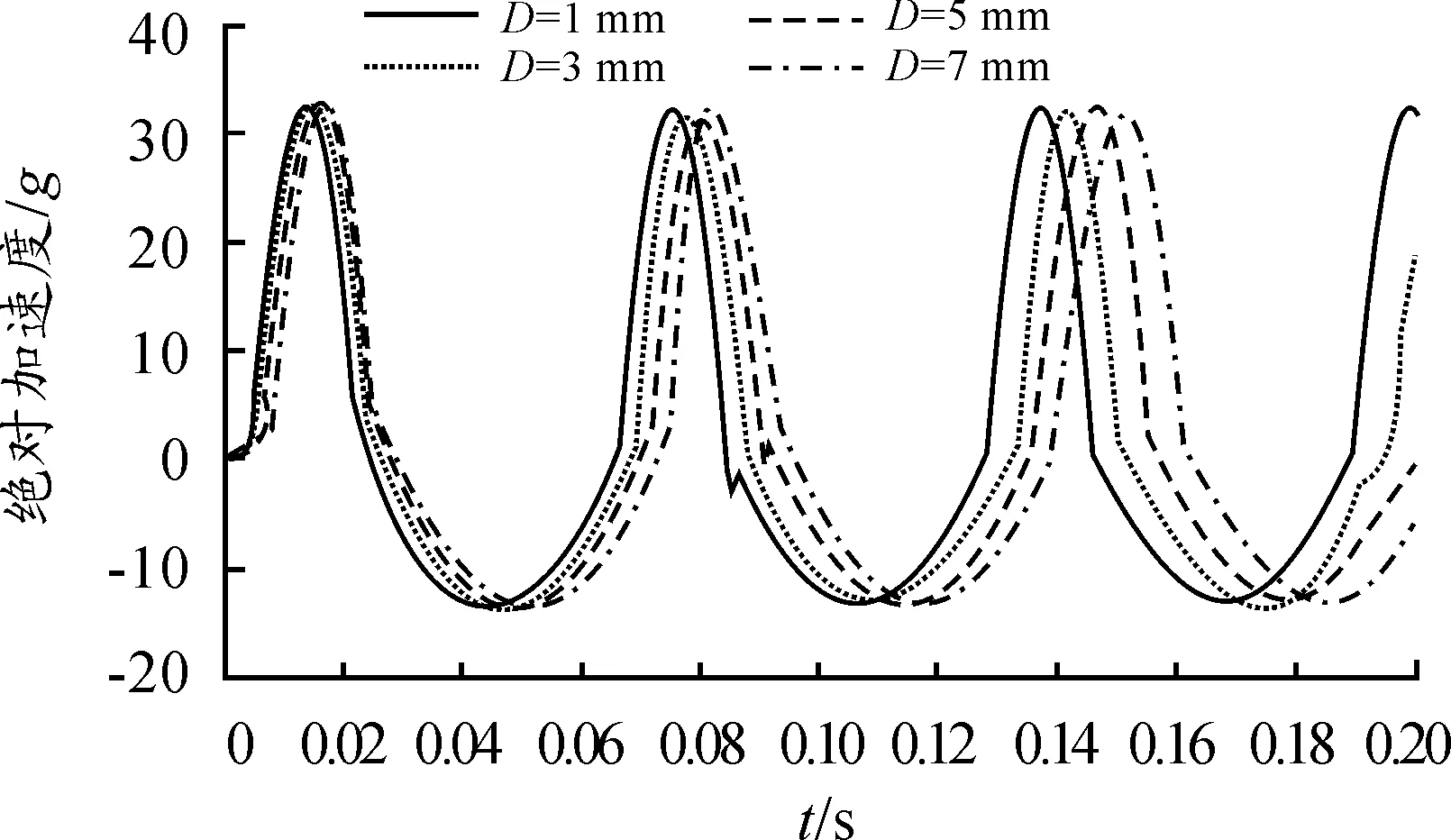
图6　不同安装间隙下绝对加速度响应曲线

图7　绝对加速度幅值随限位器间隙的变化曲线

从图7可以看出，绝对加速度幅值随着限位器安装间隙的增加先增加，后减小，在限位器安装间隙Δx=3mm时绝对加速度幅值达到最大值。

为了进一步确定绝对加速度幅值最大值是否出现在Δx=3mm，缩小安装间隙的间隔，取限位器安装间隙为2mm，2.5mm，3mm，3.5mm，4mm进行研究，绝对加速度幅值随限位器间隙的变化曲线如图8所示。绝对加速度幅值仍随限位器安装间隙的增加先增加，后减小，仍在限位器安装间隙Δx=3mm达到绝对加速度幅值最大值。因此，在设计限位器时，应避免限位器的安装间隙Δx=3mm。

3.3限位器刚度对系统响应的影响

取限位器刚度k2为1k1、3k1、5k1、7k1、9k1，研究限位器刚度对绝对加速度响应幅值和相对位移响应幅值的影响。不同安装间隙下相对位移幅值随限位器刚度的变化如图9所示，在任意确定的安装间隙下，随着限位器刚度的增加，相对位移幅值减小，二者存在负相关关系。不同安装间隙下绝对加速度幅值与限位器刚度曲线如图10所示。

图8　绝对加速度幅值随限位器间隙的变化曲线

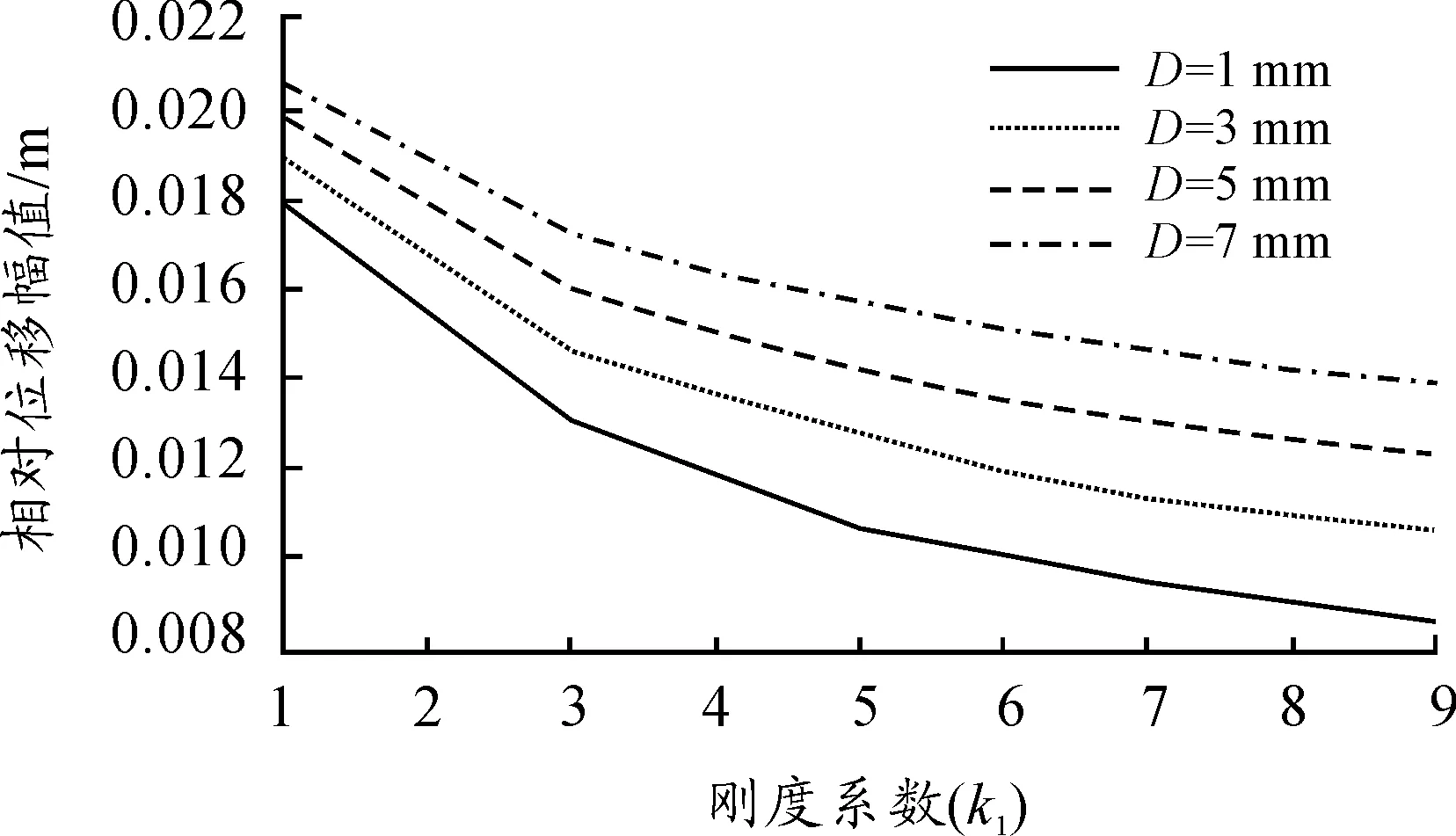
图9　不同安装间隙下相对位移幅值与限位器刚度曲线

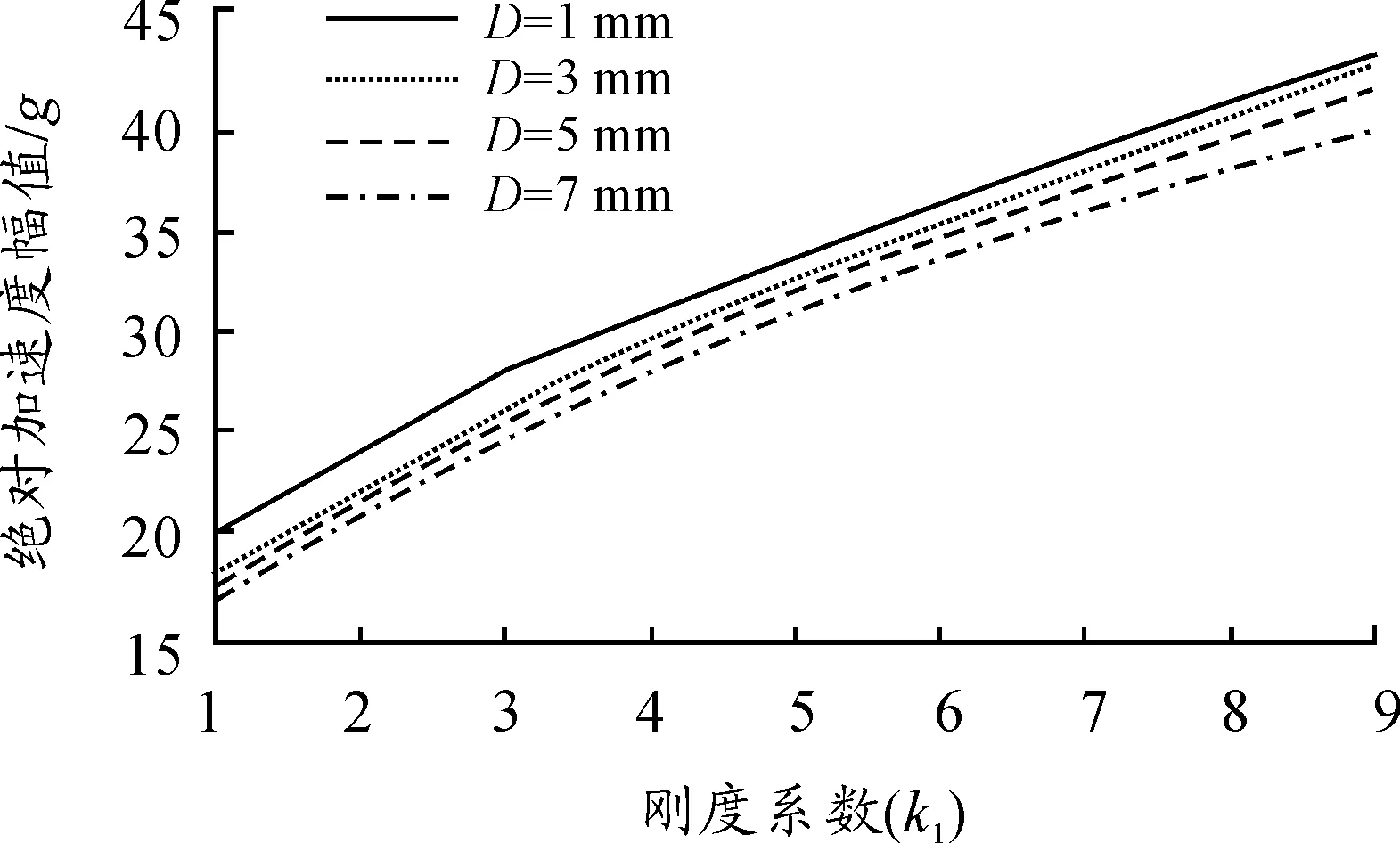
图10　不同安装间隙下绝对加速度幅值与

从图10可以看出，对于任意确定的安装间隙，系统绝对加速度幅值随着限位器刚度的增加而增大，二者存在正相关关系。

4　结论

本文探讨了单自由度隔振抗冲系统增加限位器后对系统抗冲性能的影响。通过上面的推导，可以得出以下结论：

1) 隔振抗冲系统中增加限位器，可以有效减小系统相对位移响应，但是以系统加速度增大为代价，因此限位器不能滥用，必须结合系统的抗冲要求找到二者的均衡点；

2) 限位器安装间隙对系统冲击响应有明显影响，限位器安装间隙越大，系统相对位移响应幅值越大；

3) 绝对加速度幅值随着限位器间隙的增大先增大，后减小，在Δx=3 mm时绝对加速度幅值达到最大值。本文建议设计限位器时应避开加速度响应幅值最大的安装间隙；

4) 限位器刚度越大，系统相对位移响应幅值越小，绝对加速度幅值越大。因此，在保证不影响系统隔振效果的前提下，应该尽量减小安装间隙。

[1]汪玉，华宏星.船舶现代冲击理论及应用[M].北京:科学出版社，2005.

[2]马炳杰，沈建平，王志刚.弹性限位器对双层隔振装置抗冲击性能影响分析[J].噪声与振动控制，2011 31(6)：72-75.

[3]赵存生,唐钊,唐斯密.刚度分段线性系统抗抗冲击等效线性化研究[J].噪声与振动控制,2010,30(9):24-27.

[4]唐思密，朱石坚，楼京俊.半主动干摩擦阻尼器在隔振系统中的抗冲击优化设计研究[J].振动与冲击，2012， 31(1)：11-15.

[5]赵应龙，何 琳，黄映云，等.限位器对隔振系统抗冲击性能的影响[J].振动与冲击，2005，24(2)：71-76.

[6]翁雪涛，朱石坚，何琳.限位器抗冲击计算[J].中国造船，2002，43(2)：85-89.

[7]单树军,何琳.速度阶跃法计算冲击响应幅值的误差原因和适用条件研究[J].振动与冲击,2007,26(1):91-94.

[8]许庆新,沈荣瀛.带限位器的隔振系统冲击动力学仿真[C]//第八届全国振动理论及应用学术会议论文文集摘要.上海，2003.

[9]汪玉,胡刚义,华宏星.带限位器的船舶设备非线性冲击响应分析[J].中国造船，2003，44(2)：39-44.

[10]林道福.带限位器的浮筏隔振系统的冲击响应分析[D].上海：中国科学院上海冶金研究所,2000.

(责任编辑周江川)

Research on Subsection Modeling Method of Shock Resistance Performance of the Single Stage Vibration-Isolating System with Displacement Restrictors

LI Xing-jun1, ZHAO Jian-hua2, ZHANG Chun-hui2

(1.Unit 11, Naval East Fleet Headquarter, Ningbo 315000，China；2.Power Engineering College, Naval University of Engineering of PLA, Wuhan 430033, China)

When marine equipments adopted isolation mounting device is impacted by large shock load, the relative displacement amplitudes of the isolating system may be larger than the allowable deflection of the pipes or even the equipments. Therefore, under the premise of ensuring the amplitude of the acceleration response in a bear range, appropriate displacement restrictors are needed in isolation mounting to restrict the amplitudes. Taking single-stage isolating systems as the research object, and based on Duhamel integral, the subsection model was established. The different response characteristics with or without restrictors were analyzed. The changes of the shock resistance performance were also analyzed in the case of different main restrictor parameters. The conclusions can be used to guide the design of the restrictor.

restrictor; stiffness; gap; shock resistance performance

2016-02-01；

2016-03-25

国防十二五预研基金(4010304030202 )

厉行军(1973—)，男，高级工程师，主要从事动力机械结构优化研究。

10.11809/scbgxb2016.08.007

format:LI Xing-jun, ZHAO Jian-hua, ZHANG Chun-hui.Research on Subsection Modeling Method of Shock Resistance Performance of the Single Stage Vibration-Isolating System with Displacement Restrictors[J].Journal of Ordnance Equipment Engineering,2016(8):29-32.

O381；U664

A

2096-2304(2016)08-0029-04

【装备理论与装备技术】