“认识方程”教学实录及思考

殷智强

“认识方程”教学实录及思考

殷智强

课前思考

方程与不等式是刻画数量关系的重要数学模型。“认识方程”的教学应将重心放在体验方程模型的建立，体会方程思想上，教学难点则是如何引导学生学会顺向思考，会用方程表示事物之间的数量关系。

通过前面四年的数学学习，学生已经积累了用算术方法解决问题的经验，能够运用算术方法快速地找到问题的答案。在这一过程中，学生运用的是以问题为导向的逆向思维。所以在列方程的过程中，由于受算术解题方法经验的影响，学生习惯于把未知数作为目标，然后列式计算。而方程本质上是阐述一个事实，不以解决问题为目标，表达的是题目中最基本的等量关系，体现的是一种顺向思维。逆向思维和顺向思维体现了解决问题的两种不同思考方向。在小学阶段，由于解决的问题尚不复杂，许多问题其实都可以通过逆向思考的方式予以解决。而初中、高中阶段的题目则需要通过顺向思考列出方程，最后通过解方程得以解决。所以“认识方程”的教学目标不能停留在方程的概念性描述上，而应让学生学会顺向思维，获得解决问题的另一种方法。因此在教学时，教师要通过巧妙的教学设计，逐步向学生渗透顺向思考的方式，让顺向思考列方程成为一种习惯。

教学过程

一、导入

师：仔细观察下面这些图片，它们都有一个什么共同点？

生：这些标志当中都用到了天平。

师：天平有什么特点？

图1　

生1：如果天平两边的质量相等，天平就会保持平衡；如果天平两边的质量不相等，天平就会倾斜，天平重的一端就会沉下去，轻的一端就会翘起来。

师：是的，这里就是利用天平的特点来象征公平与正义。在数学学习中，我们也会利用天平的特点解决一些问题。老师这里就有一台天平。（课件呈现天平并进行介绍）

二、新授

1.根据数量关系列算式

师：（出示图2）你看到了什么？

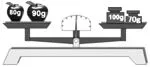
图2　

生2：天平的左边放了两个苹果，一个重80克，一个重90克；天平右边有两个砝码，一个重100克，一个重70克，天平保持平衡。

师：你是怎么看出天平保持平衡的？

生2：天平的指针指向正中间。

师：那你能用一个算式表示出它们的数量关系吗？生2：80+90=100+70。

师：（出示图3）你又看到了什么？

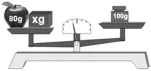
图3　

生3：天平的左边放了一个重80克的苹果和一块积木，天平的右边放了一个重100克的砝码，天平向左边倾斜。

师：天平向左倾斜说明了什么？你能像刚才一样用一个算式表示出它们之间的数量关系吗？

生3：80+一块积木＞100。

生4：这样写太麻烦了，我们可以将这块积木的质量假设为x克，用算式表示为80+x＞100。

师：太棒了，你居然想到了用字母表示这块积木的质量。但是一定要将这块积木的质量假设为x克吗？设为其他字母可以吗？（可以）只是我们通常将其设为x克。要使天平保持平衡，我们该怎么调整砝码？

生5：可以在天平的右边继续放砝码。

师：那好，在天平的右边增加一个重100克的砝码，看看天平两边又会发生什么样的变化（如图4所示）。

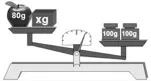
图4　

生6：右边的重一些。

师：那你能够根据这幅图列出一个算式吗？生6：80+x＜200。

师：这时的天平还是不平衡，我们该怎样调整砝码呢？你是怎样想的？

生7：说明天平左边物体的总质量在100克和200克之间，增加的这个100克的砝码太重了，可以换小一点的试试。

师：那好，我们将这个100克的砝码换成一个50克的砝码，看看结果怎么样（如图5所示）。（天平平衡了）你能根据这幅图再列出一个算式吗？

图5　

生8：80+x=150。

师：老师这里买了一个重150克的苹果，如果将其放在天平的左边，闭上眼睛想一想，天平两边会发生怎样的变化？能列出一个式子吗？

生9：天平左边会沉下去，因为150＞100+30。

师：我很好奇，如果将这个苹果咬掉一口后放到天平的左边会怎么样？

图6　

生10：天平还是向左边倾斜。

生11：不一定，要看咬掉的这一口有多重。如果刚好是20克，天平会保持平衡；如果重于20克，天平会向右边倾斜；如果小于20克，天平会继续向左边倾斜。

师：同意吗？说得真好。那你能用式子表示出来吗？

生11：150-x＜130，150-x=130，150-x＞130。

2.对式子进行分类整理

师：同学们，通过刚才的学习我们列出了8个算式。你能将它们按照一定的标准分成两类吗？说说你的想法。

①80+90=100+70②80+x＞100

③80+x＜200④80+x=150

⑤150＞130⑥150-x＜130

⑦150-x=130⑧150-x＞130

生：可以按是否为等式分类；按是否含有字母分类。

师：大家在分类时用到了两个标准：是否为等式和是否含有字母。请仔细观察两个特别的算式④和⑦。你知道为什么说它们特别吗？

生12：因为它们既是等式又含有字母。

师：对，像这样含有未知数的等式，在数学里我们称为方程。这节课我们认识了数学王国里的一位新成员——方程。（板书课题：认识方程）你能告诉大家方程具有什么特点吗？

生13：方程有两个特点，一是必须含有字母，二是必须为等式。

师：了不起。请你继续完成下列练习题（课件出示图7）。

“全人”是指全面发展的人、具有主体性且能够把握自己命运的人。因此，“全人教育”强调人的整体发展，尊重个体的多样性，其目的就是培养有道德、有知识、有纪律、有能力，和谐发展的“完人”[7]。现阶段，我们所有的教育工作者其重要使命是要培养“通德、通识、心智和谐”的人，大学英语教师最直接的方法就是在课程教学设计中彰显和体现此观念及其理论。不难发现本次设计中的几处全人教育理念：女性地位提高、女性自我意识觉醒、客观公正地评价反馈等，特别是写作作业，同学会用真实的经历和情感描写自己的母亲，对于内敛保守的中国人来讲，这是多么好的一次机会！

图7　

生14：1号肯定是方程，既含有未知数又是等式。

生15：2号可能是方程，也可能不是方程。因为只知道它是一个等式，不知道墨水后面是不是未知数。

3.巩固练习

师：请根据图8提供的信息分别列出方程。

图8　

生16：x+90=120。

生17：x+x+x+x=190，或者4x=190。

师：刚才我给了大家天平，让大家根据相关信息列出方程。现在没有天平，大家还能列出方程吗？（出示题目：3包相同的饼干，总质量是210克，每包饼干的质量是多少克？）

生18：3x=210。

生18：x表示一包饼干的质量，3x就表示3包饼干的质量，题目中已经告诉我们3包饼干的总质量是210，所以方程是3x=210。

师：那也就是说我们先找到未知量，并将其假设为x，然后想办法找到题目中的等量关系列方程。那再来一道题：一个长方形的长为13厘米，周长为40厘米，长方形的宽为多少厘米？

生19：长方形的周长计算公式是（长+宽）×2，假设长方形的宽为x厘米，这道题可列方程为（13+x）×2=40。

师：你是利用长方形周长的计算公式列方程。那方程究竟有什么好处呢？（出示例题：王老师带100元到文具店为学生购买奖品。笔记本每本6元，她购买了4本，还买了8支钢笔，售货员找回10元，你知道王老师买的钢笔单价是多少吗？）你能用方程表示出题中的数量关系吗？

生20：6×4+8×x=100-10。

师（故作疑惑状）：这个方程这么长，谁能帮我翻译一下，让大家都明白？

生21：笔记本每本6元，买了4本，6×4表示买笔记本花的钱；将钢笔的单价假设为x元，买了8支，8×x表示买钢笔花的钱；6×4+8×x表示所花出去的总钱数；100-10表示的也是所花出去的总钱数，所以相等。

师：现在我终于明白了，一段看起来很长很复杂的文字，用方程表示出来更简洁明了。

（作者单位：长沙市芙蓉区育才学校）

点评

从算术向代数过渡，是学生数学学习的重要转变，也是重要的进步。代数研究的对象不仅包括数，还包括符号。处理符号是代数的本质特征。在代数里，用字母或其他符号表示数、表示性质、表示关系、表示运算等，就把数与数的关系推广到了一般。

学生在算术学习过程中形成了一些基本的观念。这些观念中，有的与代数思维是相悖的。比如对运算的理解。在算术里，2+3表示的是一个运算过程，即把2和3加起来。在代数里，a+b不仅表示一个过程，还可以表示一个对象，即a与b的和。又如对等号（“=”）的理解。在算术里，学生倾向于把“=”理解为“宣布一种结果”。2+3=5，这里的“=”被认为是宣布2+3的结果。有这种认识的学生，难免会写出这样的错误式子2+3=5-1=4+6=10。而在代数里，“=”表示一种关系，等号两边是表示同一个东西。

方程的认识，关键是对这种关系的认识。这里的关系，当然是指数量关系。所谓数量关系，就是指数量之间的彼此依存与彼此约束。比如我有一些零钱，去商店买东西花掉了一些，还剩下一些。这里有三个数量，它们之间是有关系的。比如剩下的那些钱一定比原有的钱要少。这种关系就约束了这两个量不可能随意取值：在这里，原来10元，剩下8元，这是可能的；原来8元，剩下10元，通常就是不可能的。这种关系用不等式来刻画。又如剩下的钱加上花掉的钱，一定等于原有的钱。这种关系也约束了这三个量不可能任意取值。这种关系用等式来刻画。如果在一个等式里有未知数，我们就把这个等式叫做方程。因为这个等式反映了数量间的一种约束关系，其中的一个未知数不能任意取值。如果只有一个未知数的话，通常可以求出来。这就是解方程。

殷老师执教的“认识方程”一课，就是强调学生对数量关系的理解。天平的左边放了两个苹果，一个重80克，一个重90克；天平的右边有两个砝码，一个重100克，一个重70克，天平保持平衡。这4个苹果的质量间满足一种关系：80+90=100+70。这个等号不是通过计算、比较左右两边的结果得到的，而是通过观察天平得到的。同样，天平的左边放一个重80克的苹果和一块积木，天平的右边放一个重100克的砝码，天平向左边倾斜。这三个量之间又有一种关系，这种关系用不等式刻画：80+x＞100，这里的大于号同样不是通过计算、比较左右两边的值得到的（事实上，不等式左边根本无法计算出一个具体结果来）。左边放一个重150克的苹果，右边放100克和30克的砝码各一个，天平偏左，用150＞100+30刻画。现在，若把苹果咬掉一口，再放回去，会如何？如此，让学生不断加深对数量关系的理解：在这里，刻画数量关系的有不等式和等式。我们把目光集中到等式上来，如果等式里有未知数，就被称为方程。这里的分类，不仅是对那些式子的分类，也是对式子背后的数量关系的分类。

不仅有有形的天平，还有无形的天平。长方形的长、宽和周长之间有可以用等式刻画的数量关系，若其中有未知数，就是方程。王老师带100元到文具店为学生购买奖品。笔记本每本6元，她购买了4本，还买了8支钢笔，售货员找回10元。这些数量之间也有可以用等式刻画的关系，而钢笔的价格未知，刻画这些数量之间关系的等式就是方程。

在教学中，也可以适当引导学生关注数量关系对其中的数量的约束。比如天平的左边放一个重80克的苹果和一块积木，天平的右边放一个重100克的砝码，天平向左边倾斜。80+x＞100，这个不等式约束了积木的质量：30克是可能的，但10克是不可能的。不等式通常把其中的未知数约束在了某个范围内。而对于只有一个未知数的方程，我们往往能确定其中的未知数。这个过程事实上就是用方程解决问题。

（长沙市教育科学研究院张新春）