采用自适应字典学习的In SAR降噪方法

罗晓梅12索志勇3刘且根24

（1.西安电子科技大学综合业务网理论及关键技术国家重点实验室，陕西西安 710071；2.南昌大学信息工程学院，江西南昌 330031；3.西安电子科技大学雷达信号处理国家重点实验室，陕西西安710071；4.中国科学院劳特伯生物医学成像研究中心，广东深圳 518055）

采用自适应字典学习的In SAR降噪方法

罗晓梅1，2，索志勇3，刘且根2，4

（1.西安电子科技大学综合业务网理论及关键技术国家重点实验室，陕西西安 710071；2.南昌大学信息工程学院，江西南昌 330031；3.西安电子科技大学雷达信号处理国家重点实验室，陕西西安710071；4.中国科学院劳特伯生物医学成像研究中心，广东深圳 518055）

提出了一种基于字典学习的干涉合成孔径雷达相位降噪算法.首先利用字典学习，建立了干涉相位滤波的优化模型.鉴于该模型非凸难以求解，采用分裂技术和增广拉格朗日框架，获得松弛后的基于l1范数正则化的优化模型，然后引入交替方向乘子法对松弛后的问题求解，获得最终的相位滤波结果.通过InSAR复相位数据训练字典，从稀疏表达式重建所需的复相位图像.对仿真数据和实测数据的处理显示这种新的InSAR相位降噪方法在残点数、均方误差和边缘完整性保持方面优于现有的经典滤波方法.

InSAR；相位降噪；字典学习；l1范数正则化；交替方向乘子法

干涉合成孔径雷达（Interferometric Synthetic Aperture Radar，InSAR）已经广泛应用在许多领域，例如:数字地形模型（Digital Elevation Model，DEM）的获取和地表形变的监测.相位滤波是干涉处理的关键步骤之一，其目的是为了降低或消除各种相干因素引入的相位噪声，为后续的相位解缠绕和DEM生成奠定基础［1］.根据干涉相位的特点，人们提出了许多有效的相位滤波算法［2-6］.Lee自适应滤波器［2］能够有效地滤除干涉相位图中的噪声，其本质是对干涉相位的一种加权处理，然而，该滤波器需要进行局部相位解缠绕来确定滤波方向窗和加权系数，而存在噪声的相位解缠绕结果会对滤波产生不可忽略的影响.Goldstein滤波器［3］具有很好的噪声抑制能力，并且是以“块”滤波的方式进行的，具有很高的执行效率，目前应用比较广泛.但由于在处理数据过程中参数的不变性，该滤波器在噪声抑制和边缘完整性保持性能方面往往不能兼顾.文献［4］在应用区域增长法以相位变化最小为准则自适应选择滤波窗口，取得较好滤波效果，但未能考虑条纹数.文献［5］通过增加45°方向和135°方向的梯度计算，以及根据干涉图的相干系数确定条纹边缘的尺度函数两方面的改进改善权系数的选择，从而改进复数空间自适应滤波效果.但是相干系数确定的尺度函数并不是最优的.文献［6］给出了一种利用相干系数加权的最优干涉相位滤波方法，滤波效果较好.但由于选择的样本必须满足独立同分布的条件，而且由于降噪是逐个像素进行的，因此比经典的以块为基础的降噪滤波器时间长，例如:Goldstein滤波器.

1 相位滤波建模

为了简单起见，考虑大小为N×N的InSAR图像，若将图像中的像素按列排成列向量，则该图像在复域内表示成加性噪声模型为

其中，k表示像素的序列号，y（k）和u（k）分别表示含噪测量值和理想像素值（复形式），n（k）表示加性噪声.引入字典，一幅图像的每一子块yi可表示为

其中，yi∈CM2×1，yi表示从原图像中抽取大小为M×M的含噪图像子块按列排列形成的列向量；xi∈CK×1，xi表示对应图像子块yi的稀疏表示系数；字典D∈CM2×K，D表示含有K个原子di∈CM2×1的复字典；wi∈CM2×1，wi表示均值为零、方差为σ21+jσ22的加性高斯白噪声，j=（-1）1/2.

众所周知，由于InSAR相位表现出高的自相似性，因此，可以采用合适的字典基对复相位数据进行稀疏表示.通常训练采样值自相似性越高，字典的稀疏表示能力就越强［11］基于此，以块为基础的降噪优化模型为

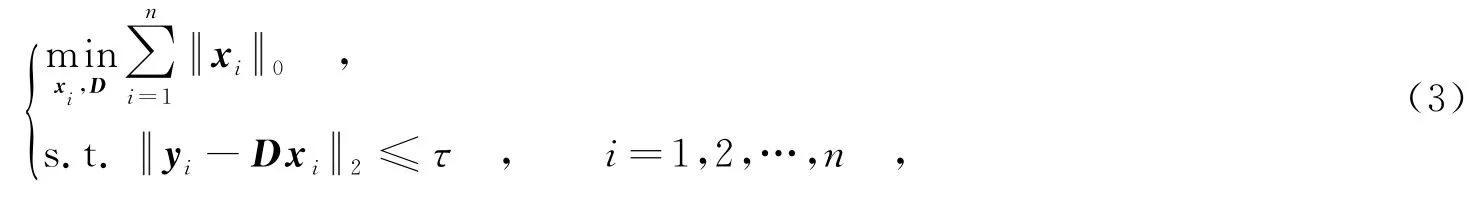
其中，n=（N-M+1）2，表示图像分块的块数.

由于约束条件中存在耦合项，式（4）是非凸的，因而可以采用块坐标轮回法［12］求解.由于字典的引入，采用标准的优化软件CVX［13］直接求解每个优化子问题是非常耗时的甚至是不能收敛的.因此，设计有效的算法求解优化问题式（4）是非常必要的.

2 基于ADMM的干涉相位滤波算法

2.1ADMM-DL算法

优化问题式（4）是带有等号约束的优化问题，因此采用ADMM算法［14］求解该问题.采用增广Lagrangian函数框架［15］，对式（4）优化变量xi和zi（i=1，2，…，n）的追踪可以等效于求解如下的i=1，2，…，n个优化子问题:

而对于优化变量D的追踪等效于求解如下的优化问题:

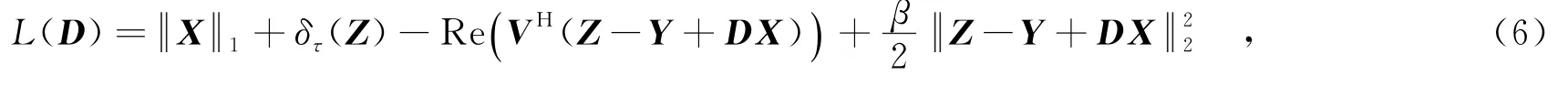
其中，vi∈CM2×1，vi表示拉格朗日乘子以及β＞0是一个罚参数.X∈CK×n，X表示由列向量｛xi｝∈CK×1组成的矩阵；Z∈CM2×n，Z表示由列向量｛zi｝∈CM2×1组成的矩阵；Y∈CM2×n，Y表示由列向量｛yi｝∈CM2×1组成的矩阵；V∈CM2×n，V表示由列向量｛vi｝∈CM2×1组成的矩阵.

引入Gaussian-Seidel迭代［12，15］，并采用ADMM技术，提出的相位滤波算法具体实现如下:

（1）计算松弛变量zk+1i，i=1，2，…，n，

（2）计算稀疏表达式xk+1i，i=1，2，…，n，

（3）计算字典Dk+1，

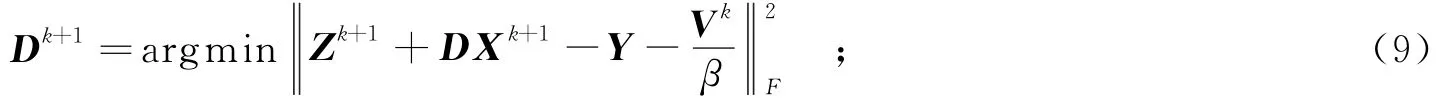
（4）计算拉格朗日乘子向量vk+1i，i=1，2，…，n，

式（7）～（10）优化子问题是凸的，其闭式解或者迭代形式分别为

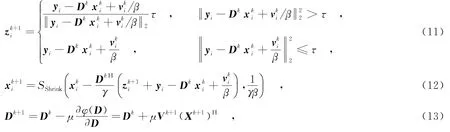
其中，SShrink表示收缩算子（Shrinkage Operator），定义为

由于篇幅的原因，式（11）和式（12）的证明略.

2.2ADMM-DL算法的计算复杂度

由于式（9）～（11）每个子问题具有闭式解或者简单的迭代形式，很容易应用到真实的InSAR图像.通过下一节对仿真数据和实测数据的处理可以获得验证.ADMM-DL算法的整个计算复杂度分析如下:

由于式（10）～（13）的计算复杂度都是O*（n M2K），其中，O*表示低阶项可以忽略.总之，ADMM-DL算法的计算复杂度是O*（4n M2K）.

3 性能分析

本节通过对仿真数据和实际数据的处理分析笔者所提算法的有效性，并与其他算法进行处理性能的对比，对比的指标包括滤波后干涉相位图的残点数量［4］，剩余相位的均方差以及相位条纹边缘的保持性等指标.

3.1仿真数据实验

通过MATLAB中的peaks函数产生一个模拟的相位曲面xyphase=appeak（N），其中，a=10，N=900.假设复相位模型的噪声方差是0.6+j0.6.使用ADMM-DL滤波器和经典的滤波方法进行滤波.文中进行性能对比的经典滤波方法包括测试均值滤波器、Goldstein滤波器和Lee滤波器.除了Lee滤波器的窗口大小是9×9，其他滤波方法窗口的大小是5×5.滤波后的图像如图1所示.

图1　仿真结果对比

为了定量分析不同滤波器的滤波性能，对残点数和滤波后剩余相位的均方差（Mean Square Error，MSE）进行统计，如表1所示.

表1　不同滤波器的残点数和MSE比较

采用ADMM-DL滤波器，按照式（11）～（13），求解优化问题式（3），获得字典D和最稀疏的表达式X= ｛xi｝，xi是式（3）的优化变量，再将二者相乘恢复出理想的InSAR相位图.从图1所示的干涉图以及表1所列的残点数和MSE可知，ADMM-DL滤波器的残点数最少并且其残余相位的均方差最小.与理想的相位图相比，采用ADMM-DL滤波器滤波后图像的边缘失真也是最小的.

3.2实测数据实验

对带有噪声的大小是882×882的实测InSAR相位图进行降噪.ADMM-DL滤波器的参数设定与场景一相同.在实际中，式（1）中的噪声可以近似成一个复的零均值、互相关矩阵与相关值γ有关的白高斯噪声，即

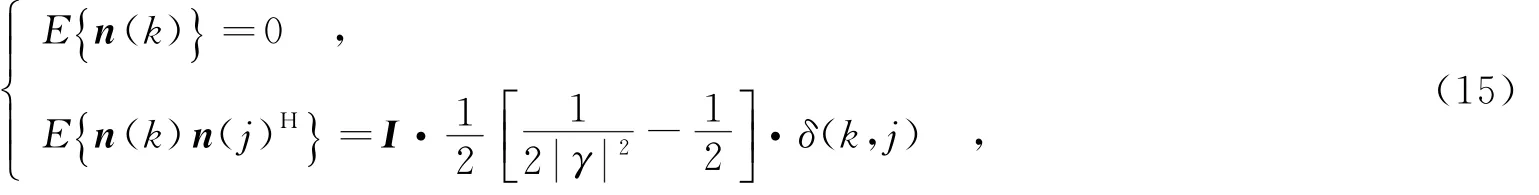
这意味着在使用ADMM算法式（7）～（10）之前必须用标准差归一化式（1）中的噪声变量n（t）.滤波后的图像如图2所示.

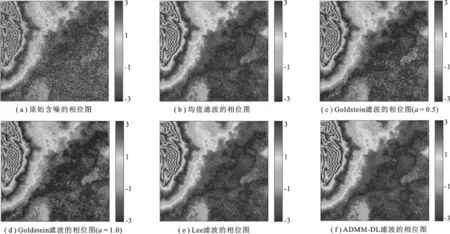
图2　实测结果对比

表2　不同滤波器的残点数比较

采用ADMM-DL滤波器，按照仿真数据实验相同的方式处理数据.从表2所示的残点数和图2显示的干涉相位图可见，ADMM-DL滤波器不但能滤除更多的噪声而且能更好地保持边缘完整性.

4 结束语

笔者提出了一种新的干涉相位滤波法，以字典学习为基础，对复InSAR数据建立了降噪的优化模型.基于Lagrangian/Bregman迭代框架，进行松弛变换和采用ADMM技术，使非凸的难解的优化问题被分解成几个凸的优化子问题，并提出了有效的ADMM-DL算法迭代计算这些子问题.在抑制噪声和滤除残点方面，文中方法的性能都优于传统的滤波方法.

［1］SUKSMONO A B，HIROSE A.Interferometric SAR Image Restoration Using Monte Carlo Metropolis Method［J］. IEEE Transactions on Signal Processing，2002，50（2）:290-298.

［2］郭交，李真芳，刘艳阳，等.一种InSAR干涉相位图的自适应滤波算法［J］.西安电子科技大学学报，2011，38（4）:77-81. GUO Jiao，LI Zhenfang，LIU Yanyang，et al.New Adaptive Noise Suppressing Method for Interferometric Phase Images［J］.Journal of Xidian University，2011，38（4）:77-81.

［3］LEE J S，PAPATHANASSIOU K P，AINSWORTH T L，et al.A New Technique for Noise Filtering of SAR Interferogram Phase Images［J］.IEEE Transactions on Geoscience and Remote Sensing，1998，36（5）:1456-1465.

［4］GOLDSTEIN R M，WERNER C L.Radar Interferogram Filtering for Geophysical Applications［J］.Geophysical Reservation Letters，1998，25（21）:4035-4038.

［5］易辉伟，朱建军，陈建群，等.一种改进的InSAR干涉图复数空间自适应滤波［J］.中南大学学报，2013，44（2）:632-641. YI Huiwei，ZHU Jianjun，CHEN Jianqun，et al.An Improved Adaptive Algorithm for Filtering InSAR Interferogram in Complex Plane［J］.Journal of Central South University，2013，44（2）:632-641.

［6］李锦伟，李真芳，刘艳阳，等.一种相干系数加权的最优干涉相位滤波［J］.西安电子科技大学学报，2014，40（2）:25-31. LI Jinwei，LI Zhenfang，LIU Yanyang，et al.Coherence-weighted Optimum Interferometric Phase Filtering Method ［J］.Journal of Xidian University，2014，40（2）:25-31.

［7］AHARON M，ELAD M，BRUCKSTEIN A.K-SVD:an Algorithm for Designing Overcomplete Dictionaries for Sparse Representation［J］.IEEE Transactions on Signal Processing，2006，54（11）:4311-4322.

［8］RAZAVIYAYN M，TSENG H W，LUO Z Q.Dictionary Learning for Sparse Representation:Complexity and Algorithm ［C］//Proceedings of the IEEE International Conference on Acoustics，Speech and Signal Processing.Piscataway:IEEE，2014: 5247-5251.

［9］YU G S，SAPIRO G，MALLAT S.Image Modeling and Enhancement via Structured Sparse Model Selection［C］// Proceedings of the IEEE Conference on Image Processing.Piscataway:IEEE Computer Society，2010:1641-1644.

［10］KERVRANN C，BOULANGER J.Local Adaptively to Variable Smoothness for Examplar-based Image Regularization and Representation［J］.International Journal of Computer Vision，2008，79（1）:45-69.

［11］HAO H，BIOUCAS-DIAS J M，KATKOVNIK V.Interferometric Phase Image Estimation via Sparse Coding in the Complex Domain［J］.IEEE Transactions on Geoscience and Remote Sensing，2015，53（5）:2587-2602.

［12］RAZAVIYAYN M，HONG M Y，LUO Z Q.A Unified Convergence Analysis of Block Successive Minimization Methods for Nonsmooth Optimization［J］.SIAM Journal on Optimization，2013，23（2）:1126-1153.

［13］GRANT M，BOYD S.CVX:Matlab Software for Disciplined Convex Programming［EB/OL］.［2014-07-26］.http:// cvxr.com/cvx/.

［14］HE B S，YUAN X M.On the O（1/n）Convergence Rate of the Douglas-Rachford Alternating Direction Method［J］. SIAM Journal on Numerical Analysis，2012，50（2）:700-709.

［15］BERTSEKAS D P.Nonlinear Programming［M］.2nd Edition.Nashua:Athena-Scientific，1999.

［16］DAUBECHIES I，DEFRISE M，De MOL C.An Iterative Thresholding Algorithm for Linear Inverse Problems with a Sparsity Constraint［J］.Communications on Pure and Applied Mathematics，2004，57（11）:1413-1457.

（编辑:王 瑞）

InSAR noise reduction using adaptive dictionary learning

LUO Xiaomei1，2，SUO Zhiyong3，LIU Qiegen2，4
（1.State Key Lab.of Integrated Service Networks，Xidian Univ.，Xi’an 710071，China；2.Department of Electronic Information Engineering，Nanchang University，Nanchang 330031，China；3.National Key Lab.of Radar Signal Processing，Xidian Univ.，Xi’an 710071，China；4.The Paul C.Lauterbur Research Centre for Biomedical Imaging，Shenzhen Key Lab.for MRI，Chinese Academy of Sciences，Shenzhen 518055，China）

We consider the phase noise filtering problem for interferometric synthetic aperture radar （InSAR）based on the dictionary learning technique.Due to the non-convexity of the optimization problem is difficult to solve.By using the splitting technique and employing the augmented Lagrangian framework，we obtain a relaxed nonlinear constraint optimization problem with l1-norm regularization which can be solved efficiently by the alternating direction method of multipliers（ADMM）.Specifically，we firstly train dictionaries from the InSAR complex phase data，and then reconstruct the desired complex phase image from the sparse representation.Simulation results based on simulated and measured data show that this new InSAR phase noise reduction method has a much better performance than several classical phase filtering methods in terms of residual count，mean square error（MSE）and preservation of the fringe completeness. Key Words: interferometric synthetic aperture radar；phase noise reduction；dictionary learning；l1-norm regularization；alternating directional method of multipliers

TN957.51

A

1001-2400（2016）01-0018-06

10.3969/j.issn.1001-2400.2016.01.004

2014-08-02 网络出版时间：2015-04-14

国家自然科学基金资助项目（61362001，51165033）

罗晓梅（1971-），女，西安电子科技大学博士研究生，E-mail:xxmluo@gmail.com.

网络出版地址：http://www.cnki.net/kcms/detail/61.1076.TN.20150414.2046.004.html