快速随机多核学习分类算法

孙 涛，冯 婕

（西安电子科技大学智能感知与图像理解教育部重点实验室，陕西西安 710071）

快速随机多核学习分类算法

孙 涛，冯 婕

（西安电子科技大学智能感知与图像理解教育部重点实验室，陕西西安 710071）

多核学习是整合多个子核在一个优化框架内，从而寻求到多个子核之间的一个最佳线性组合，而且多核学习可以获得比单核学习更好的分类性能.受极限学习思想的启发，提出了快速随机多核学习分类方法.当满足极限学习的理论框架时，可以在构造核的过程中，对参数随机赋值，构造一种随机核.可以缩减子核的规模，加快了多核学习的计算时间，并且节省了内存空间，使得多核学习可以处理更大规模的问题.另外，通过使用经验Rademacher复杂度来分析多核学习的一般性误差，从而获得比原有多核学习更高的分类精度.结果表明，与经典的快速多核学习算法相比，文中提供的算法计算更快，占用内存空间更小，分类精度更高.

多核学习；极限学习；随机核；经验Rademacher复杂度

核学习是机器学习中的重要领域.在分类问题中，如果不同种类的数据混杂在一起，在当前维数空间内，可能无法找到一个分类面对它们加以区分.此时，就需要把原始数据通过一个映射函数投影到髙维空间，在髙维空间内把它们区分开.这种方式称为核学习，又称为核技巧［1］.核学习因为其在解决线性不可分问题上的卓越性能，被广泛应用于分类算法［2-4］.多核学习（Multiple Kernel Learning，MKL）［5］是核学习新的研究热点.当对一个目标样本进行分类时，该目标可能呈现出多种特征，需要从中选取出最适合分类的特征.多核学习可以把每一种特征都构成一个单独的子核，然后把多个子核放到一个统一框架内，从而选择出最合适的子核组合，即选出最合适的特征来进行分类.与其他特征选择算法相比，多核学习可以把特征选择问题转变成一个凸优化问题，从而采用经典优化得到最优解.

多核学习往往可以取得比单核学习更好的结果，但是相对应的是时间复杂度和空间复杂度的增加.自从多核学习算法提出以来，研究者们就热衷于如何提高多核学习的计算速度.早期，Bach等［6］把多核学习问题转变成二次锥形规划问题来求解，在算法复杂度上得到一定的降低，但依然不是很理想.后来，Sonnenburg等［7］使用最小最大化模型来描述多核学习问题，用交替优化的方法来求解，大大加快了算法的计算时间.在这个模型的基础上，研究者们为了进一步加快优化速度，相继提出了梯度下降的方法［8］、基于Lasso的方法［9］和解析优化的方法［10］.

上述多核学习的加速算法，都是着重于如何建立更快的优化模型，从而加快优化速度.笔者则考虑通过缩减子核的规模来达到加速的目的，并从极限学习机（Extreme Learning Machine，ELM）［11-12］得到了启发. ELM以单隐层前馈神经网络为平台，提供了一种无需参数调节的分类方法.按照ELM理论的描述，如果隐层节点的数目足够多，在隐藏节点的权重随机赋值的情况下，给定一个在任意区间无限可导的激活函数，SLFN就可以无限逼近拟合输入样本集.如果减少了子核的规模，不仅加快了优化的速度，而且节省了内存空间，使得笔者的方法可以处理更大规模的问题.

另外，通过使用经验Rademacher复杂度［13］来分析多核学习的一般性误差，发现多核学习一般性误差的上确界受到子核数目的影响.如果子核数目过多，误差的上确界增高，从而导致分类精度的下降.随机多核学习在保持训练误差不变的同时，通过降低子核的数目降低了多核学习一般性误差的上确界，从而理论上保证了文中方法可以获得比原有多核学习更好的分类结果.

1 多核学习框架

在单核学习中，依据优化的最终目标不同，有支撑矢量机（Support Vector Machine，SVM）、核判别分析、核最近邻等.当单核学习变为了多核学习的时候，按照最终的优化目标不同，分为了不同的算法.由于SVM分类不用考虑数据的分布特性，有着更广泛的应用环境，所以，文中利用SVM给出多核学习对偶式的公式为

2 快速随机多核学习

2.1构造随机核

在上节介绍了子核的参数设置对多核学习的时间和空间复杂度的巨大影响.如果有一种无需参数调节的核，就可以减少子核的规模，降低多核学习的计算时间和内存存储.Huang等［11］提出了一种无需参数调节的分类方式:ELM算法.先回顾ELM的逼近拟合理论.

定理1 对于任意N个输入样本，给定一个在任意区间可以无穷可导的激活函数和L个隐藏层节点，对隐藏层节点的权重和偏差随机赋值，ELM可以无误差地逼近这N个独立样本.

给定一个含有L个隐藏层节点和M个输出节点的单隐层前馈神经网络.训练集x=（x1，x2，…，xN），含有N个样本，每个样本的维数是d，输出结果是f（x）.G（ai，bi，xi）是满足ELM理论的激活函数，其中，a，b都是随机赋值的.βi是隐藏层的输出权重，它满足如下的公式:

其中，

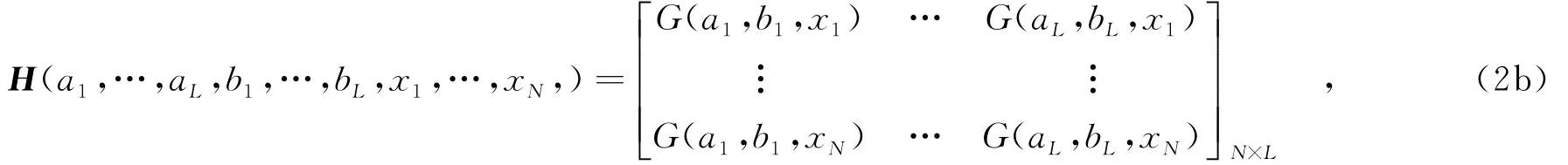
H称作隐层输出矩阵，第i列表示输入样本在激活函数G（ai，bi，x）映射下的第i个隐层节点的输出，T=［tT1，…，tTN］T，是训练样本的类标.

由上文的介绍可知，当输入样本被激活函数映射到一个L维空间后，通过一定的操作可以无误差的逼近任何一个输入样本的类标.这意味着不同种类的样本在这个L维空间内是完全可分的.按照线性不可分问题的解决思路:寻找一个髙维映射函数，把原始数据映射到一个足够髙维的空间，把原来不可分的数据完全可分，而核矩阵就等价于髙维映射函数与它的转置做内积.在ELM中，如果把激活函数看作髙维映射函数，L维空间就是那个足够髙维的空间，可以直接把激活函数和它的转置做内积K=H·HT来构成核矩阵.由于在构造核过程中的参数可以随机赋值，不需要调节参数，所以称之为随机核.

2.2一般性误差的理论分析

虽然随机核的构造加快了多核学习的计算速度，但是否会影响分类的精度依然未知.这里，通过对多核学习的一般性误差分析，来判断随机核对分类精度的影响.

首先，回顾一下模式识别的一个重要理论.

定理2 F是一个定义在集合X上输出为｛±1｝的函数.P是在集合X上的概率分布.假设（X1，Y1），…，（Xn，Yn）与（X，Y）相对于P独立同分布的，则F中的每个子函数f以概率至少1-δ满足

其中，σ1，…，σN∈｛-1，+1｝，是独立均匀分布的随机变量.E代表着期望操作.利用McDiarmid不等式，F中的每个子函数f以概率至少1-δ满足

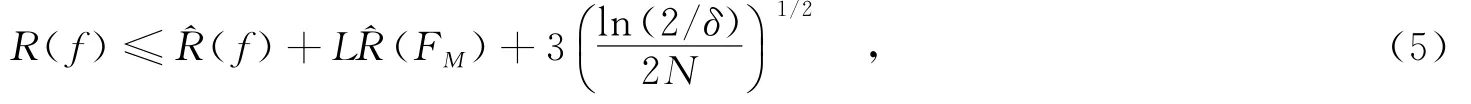
其中，M是子核的数目.L代表损失函数（例如最小平方损失和hinge loss损失）.当δ固定时 （，ln（2/δ）/ （2N））1/2是一个常数.

从文献［10］的结论中，可以得到多核学习L1约束的经验Rademacher复杂度为

其中，η0=23/22.R是一个满足Km（x，x）≤R2的常数.

假设L是一个关于ρ的损失函数，把式（6）代入式（5）中，可以得到

3 实验结果分析

胃癌每年在全球影响着大约800 000的人.胃癌的术前分期对于胃癌的治疗具有非常重要的意义.当前，肿瘤诊断系统是胃癌分期的一个标准系统.其中的淋巴结诊断又是肿瘤分期的一个重要组成部分.淋巴结诊断为手术治疗提供了非常重要的参考.

传统上，淋巴结尺寸被用来作为淋巴结诊断的参考指标.后来，临床医学发现仅仅使用淋巴结尺寸是不足够的.因为大的淋巴结可能是由发炎引起的.而那些不被关注的小淋巴结有可能是真正的转移淋巴结.所以，仅仅依赖淋巴结的尺寸，有可能形成误判.多项生理指标的组合使用就成为了淋巴结诊断的必然选择.但是人的生理指标有很多，哪些生理指标是跟淋巴结诊断相关的，在临床上还暂未定论.

在这里把生理指标的选择问题转变为一个优化选择问题.多核学习被用来求解这个问题.每个指标对应着一个子核，那么优化选择子核的过程就等价于选择最优指标的过程.经过优化求解以后，可以得到多个指标的一个最佳加权组合，它就可以用来检测淋巴结是否转移.

该实验的实验数据来自北京大学医学院癌症研究中心.该数据包含1000个病例，每位病人拥有18个生理指标.它们分别是性别、年龄、肿瘤位置、肿瘤最大半径、肿瘤厚度、肿瘤模式、肿瘤模式、浆膜入侵、入侵深度、博尔曼（Borrmann）类型、加强模式、淋巴结个数、最大淋巴结尺寸、淋巴结数目、最大淋巴结尺寸、淋巴结station、淋巴结的CT衰减、淋巴结的短径与长径比、淋巴结分布、病理类型和血清癌培抗原（CEA of serum）.

对比实验包括简单多核学习［8］，基于Lasso的多核学习［9］和Lp范数多核学习［10］.使用RBF核，其中的核参数，提供了10个候选值［2-3，2-2，…，26］.因此，每个指标对应于有着不同核参数的10个子核.总共拥有18×10=180个子核.

对于随机多核学习，每个指标被用来构造一个随机核.激活函数，选择RBF激活函数.影层的节点数是2 000，总共有18个候选子核.每次运行，随机抽取［30%，50%，70%］的样本作为训练样本，剩余的样本作为测试.整个过程被重复50次.平衡因子C由10次交叉验证来确定.

表1　淋巴结转移分类结果比较

如表1所示，随机多核学习在所有3种不同比例的训练样本集上，分类精度都要优于其他3种多核学习算法.由于减少了子核的规模，随机多核学习使用了最少的训练时间.而且随机多核学习需要更少的子核数目，它一定程度上对应着需要的特征数目.这在临床医学上是非常重要的.因为它可以避免病患做一些不必要的，或者有风险的医疗检查.

4 结束语

笔者提出了一种随机多核学习分类算法，缩减了子核的规模，从而加快了多核学习的训练时间，节省了内存存储空间，并且提高了分类精度.在淋巴结检测数据库上的实验，充分验证了该算法的优良性能.

随着当前信息量的爆炸式发展，要处理的分类问题规模将越来越大，借助语义先验的方法，进一步减少算法的运算时间将是下一步工作的重点.

［1］KWAK N.Nonlinear Projection Trick in Kernel Methods:an Alternative to the Kernel Trick［J］.IEEE Transactions on Neural Networks and Learning Systems，2013，24（12）:2113-2119.

［2］SHAO Z F，ZHANG L，ZHOU X R，et al.A Novel Hierarchical Semisupervised SVM for Classification of Hyperspectral Images［J］.IEEE Geoscience and Remote Sensing Letters，2014，11（9）:92-97.

［3］WON K，SAUNDERS C，PRÜGEL-BENNETT A.Evolving Fisher Kernels for Biological Sequence Classification［J］. Evolutionary Computation，2013，21（1）:81-105.

［4］李映，焦李成.基于核Fisher判别分析的目标识别［J］.西安电子科技大学学报，2003，30（2）:179-182. LI Ying，JIAO Licheng.Target Recognition Based on Kernel Fisher Discriminant［J］.Journal of Xidian University，2003，30（2）:179-182.

［5］SUN T，JIAO L C，LIU F，et al.Selective Multiple Kernel Learning for Classification with Ensemble Strategy［J］. Pattern Recognition，2013，46（11）:3081-3090.

［6］BACH F，LANCKRIET G，JORDAN M.Multiple Kernel Learning，Conic Duality，and the SMO Algorithm［C］// Proceedings of 21th International Conference on Machine Learning.New York:ACM，2004:41-48.

［7］SONNENBURG S，RATSCH G，SCHAFER C，et al.Large Scale Multiple Kernel Learning［J］.Journal of Machine Learning Research，2006，7（1）:1531-1565.

［8］BACH F，RAKOTOMAMONJY A，CANU S，et al.Simple MKL［J］.Journal of Machine Learning Research，2008，9:2491-2521.

［9］XU Z L，JIN R，YANG H Q，et al.Simple and Efficient Multiple Kernel Learning by Group Lasso［C］//Proceedings of the International Conference on Machine Learning.London:Elsevier Limited，2010:1175-1182.

［10］KLOFT M，BREFELD U，SONNENBURG S，et al.Lp-Norm Multiple Kernel Learning［J］.Journal of Machine Learning Research，2011，12:953-997.

［11］HUANG G B，WANG D H，LAN Y.Extreme Learning Machines:a Survey［J］.International Journal of Machine Learning and Cybernetics，2011，2（2）:107-122.

［12］CHEN J Y，ZHENG G Z，CHEN H J.ELM-Map Reduce:MapReduce Accelerated Extreme Learning Machine for Big Spatial Data Analysis［C］//IEEE International Conference on Control and Automation.Washington:IEEE Computer Society，2013:400-405.

［13］CORTES C，MOHRI M，ROSTAMIZADEH A.Generalization Bounds for Learning Kernels［C］//Proceedings of the 27th International Conference on Machine Learning.London:Elsevier Limited，2010:247-254.

（编辑:王 瑞）

Fast randommultiple kernel learning for classification

SUN Tao，FENG Jie
（Ministry of Education Key Lab.of Intelligent Perception and Image Understanding，Xidian Univ.，Xi’an 710071，China）

Multiple kernel learning（MKL）combines multiple kernels in a convex optimization framework and seeks the best line combination of them.Generally，MKL can get better results than single kernel learning，but heavy computational burden makes MKL impractical.Inspired by the extreme learning machine（ELM），a novel fast MKL method based on the random kernel is proposed.When the framework of ELM is satisfied，the kernel parameters can be given randomly，which produces the random kernel. Thus，the sub-kernel scale is reduced largely，which accelerates the training time and saves the memory. Furthermore，the reduced kernel scale can reduce the error bound of MKL by analyzing the empirical Rademacher complexity of MKL.It gives a theoretical guarantee that the proposed method gets a higher classification accuracy than traditional MKL methods.Experiments indicate that the proposed method uses a faster speed，more small memory and gets better results than several classical fast MKL methods.

multiple kernel learning；extreme learning machine；random kernel；empirical rademacher complexity

TP775

A

1001-2400（2016）01-0036-05

10.3969/j.issn.1001-2400.2016.01.007

2014-08-31 网络出版时间：2015-04-14

国家973计划资助项目（2013CB329402）；国家自然科学基金资助项目（61272282）；新世纪人才计划资助项目（NCET-13-0948）

孙 涛（1984-），男，西安电子科技大学博士研究生，E-mail:taosun@mail.xidian.edu.cn.

网络出版地址：http://www.cnki.net/kcms/detail/61.1076.TN.20150414.2046.023.html