结合自适应稀疏表示和全变分约束的图像重建

王 勇1，冯唐智1，陈楚楚1，乔倩倩1，杨笑宇1，王国栋1，高全学2

（1.西安电子科技大学电子工程学院，陕西西安 710071；2.西安电子科技大学通信工程学院，陕西西安 710071）

结合自适应稀疏表示和全变分约束的图像重建

王 勇1，冯唐智1，陈楚楚1，乔倩倩1，杨笑宇1，王国栋1，高全学2

（1.西安电子科技大学电子工程学院，陕西西安 710071；2.西安电子科技大学通信工程学院，陕西西安 710071）

针对以二维小波变换和离散余弦变换为代表的固定正交基在图像压缩感知高分辨率重建中的局限性，提出了一种新的自适应冗余字典稀疏表示结合全变分约束的图像高分辨率重建算法.该算法以迭代过程的中间图像作为训练样本，通过自适应学习获得适合样本特征的冗余字典，它充分利用了字典原子与待重建图像的相关性，获得了待重建图像的理想完备稀疏表示，从而降低了采样率，提高了图像重建质量.最后，以全变分作为正则化条件，采用交替迭代算法求解稀疏优化问题.仿真结果表明，该算法可以在低采样率下重建出高质量的图像.

压缩感知；自适应冗余字典；稀疏表示；图像重建；全变分

在图像高分辨率重建中，稀疏表示是近年来关注的热点之一，也是压缩感知成像的核心问题之一［1］.为提高图像表示的稀疏性，一般通过小波、离散余弦等正交变换对图像进行稀疏表示.这些传统稀疏表示的优点是操作简单、理论成熟.但是这些变换存在着只能表示有限的信号特征的缺点，当信号与基函数特征不匹配时不能获得理想的稀疏表示.最近，字典作为一种有效的稀疏表示手段被引入到图像去噪、去模糊、超分辨及分类等问题中［2-7］，获得了较好的效果.在雷达图像编码领域，从已有相关图像学习出字典，并将该字典作为稀疏变换基应用在合成孔径雷达图像压缩中，取得了较好的效果.相比以小波变换为基础的JPEG2000压缩算法，该方法能够更好地保留图像的重要特征［2］.在图像去模糊方面，利用图像分块在冗余字典下具有稀疏性先验的性能，通过求解稀疏优化问题来恢复图像，获得了较好的效果［3］.采用交替迭代思想，从降质图像本身学习冗余字典，自适应地选取适合待重建图像特征的稀疏变换基，在图像去模糊和超分辨重建中取得了较好效果.在压缩感知方面，在多稀疏空间框架下根据图像局部特性自适应地选取稀疏表示基，提高了表示的稀疏性，降低了采样率［4］.

为了克服传统图像在压缩感知中采用正交基或固定字典作为稀疏变换基带来的图像重建质量低和适应性不强的问题，笔者根据多原子库自适应学习的思想，建立了图像稀疏编码模型.该模型从迭代重建过程的中间图像学习得到冗余字典，充分利用了字典原子与待重建图像的相关性，从而获得了较理想的图像稀疏编码.利用图像在字典域具有稀疏性这一先验知识，通过求解非线性优化问题可以重建出高质量图像.由于图像重建是一个典型的反问题，为了进一步提高重建质量，需要挖掘更多的先验信息，缩小优化问题的求解范围，从而提高重建质量.全变分是一种根据自然图像离散梯度具有稀疏性这一先验知识而提出的正则化约束模型，已成功应用于图像去噪和修复等反问题中.全变分在促使重建图像平滑的同时，还对图像的边缘和纹理具有很好的保持作用［8］.笔者将全变分稀疏先验作为一种正则化项引入到重建模型中，提出了一种结合自适应稀疏表示和全变分约束的图像高分辨率重建算法（Adaptive Sparse rePresentation and Total Variation constraint reconstruction，ASP-TV），提高了图像重建质量.

1 图像稀疏重建

根据压缩感知理论，图像的稀疏表示重建过程是一个反问题.设待重建图像x∈RN×N；稀疏变换基为正交变换Ψ，Ψ∈RN×N；图像的稀疏编码x=Ψα，其中α中每一列的非零元素的个数不大于K个；观测信号y=Φx，其中Φ为观测矩阵.压缩感知理论［1］指出，若观测矩阵Φ和稀疏基Ψ不相关，可以从M≥K log（N/K）个采样中通过求解最优化问题（P1）来重建出信号x:

2 基于ASP-TV模型的图像高分辨率重建

在处理各种基于过完备稀疏表示模型的图像反问题时，传统的做法是先从自然图像库中学习出一个固定的冗余字典，然后以该字典作为稀疏变换基［9］.在图像信息丢失不太严重的情况下，固定的字典仍可以较为准确地描述数据中的主要特征，利用稀疏先验可以从低维观测信号中较为准确地恢复原始数据.但是，在图像信息损失严重的情况下，固定的字典不能很好地对图像进行稀疏表示，从而很难恢复原始图像.基于以上理论，笔者从稀疏编码和稀疏优化问题求解入手，提出ASP-TV模型.根据欠采样数据，通过反投影法重建初始图像，从该图像出发，采用交替迭代逐步逼近［10］来获得较精确的结果.该模型较传统的图像压缩感知主要有两点改进:首先，将图像的小范围分块在自适应冗余字典下具有稀疏性这一先验知识引入压缩感知，代替传统的正交变换稀疏先验知识.每次迭代都将上一次迭代获得的图像进行重叠式分块，利用K奇异值分解（K-SVD）算法［11］从这些分块中学习出冗余字典.由于分块可以很好地突出图像局部结构特点，因而从分块学习得到的字典有效地利用了图像的局部结构信息，对图像可以更好地稀疏表示，降低了采样率.此外，字典是从逐步精确的迭代过程中动态获得的，不是预先设定的固定字典，所以该字典是自适应待重建图像的，能够很好地描述图像.将该字典作为稀疏变换基，利用图像分块的真实成分在字典下是稀疏的，而伪影和噪声则是非稀疏的这一先验知识，在求解稀疏优化问题的同时去除伪影与噪声.其次，为进一步缩小求解范围，提高重建精度，将全变分正则化项引入重建模型.在去除伪影与噪声的基础上，利用自然图像离散梯度具有稀疏性的特点，使用全变分约束，通过求解带采样数据一致性项和前后两次迭代数据一致性项的二范数优化问题更新图像，进一步提高重建精度.具体求解时，采用分裂Bregman迭代法求解同时含有待恢复图像x和图像对应的稀疏编码系数α的近似零范数约束的非凸优化问题，不同于一般的求解单变量L1范数稀疏凸优化问题.ASP-TV模型的流程如图1所示.

图1　ASP-TV模型流程图

2.1自适应稀疏表示

在K-SVD算法的基础上，笔者从迭代求解过程的中间图像学习出冗余字典.由于所获得的冗余字典是从待重建图像本身学习得到的，因此该字典是自适应待重建图像的，能够很好地描述信号的特征，获得完备的稀疏表示.对图像按列处理，N×N图像的稀疏变换基为冗余字典D，D∈RN×K（K＞N），待重建信号在字典D下的稀疏编码为x，x=Dα，其中α与x都是未知的待求解量，观测信号y=Φx=ΦDα.由先验知识知待重建图像在字典D下是稀疏的，即α是稀疏的，原始图像x可以通过求解最优化问题（P2）得到:

当图像的维度N较大时，D是一个规模非常大的矩阵，对存储器要求很大，同时式（2）将是一个大尺度问题，求解较困难.为了降低对存储器的要求和求解难度，笔者在对图像进行稀疏编码时采用“分块”的策略.使用一个大小为n×n（n＜N）的窗从图像的左上角开始，分别沿横向和纵向移动，直到窗的右下角到达图像的右下角.窗每移动一个像素时将获得一个小的图像块.定义Rij（1≤i，j≤N-n+1）为从N×N的图像中取出的大小为n×n像素块的算子，则上一次迭代所得图像x（k）的全体分块可表示为

利用K-SVD算法［11］对上述图像分块xij（k）（1≤i，j≤N-n+1）进行字典学习，得到字典D（k）.本次迭代的待求解图像分块xij=Rijx在字典D（k）下的稀疏编码为xij，xij=D（k）αij，利用稀疏先验知识，有重建模型（P3）为

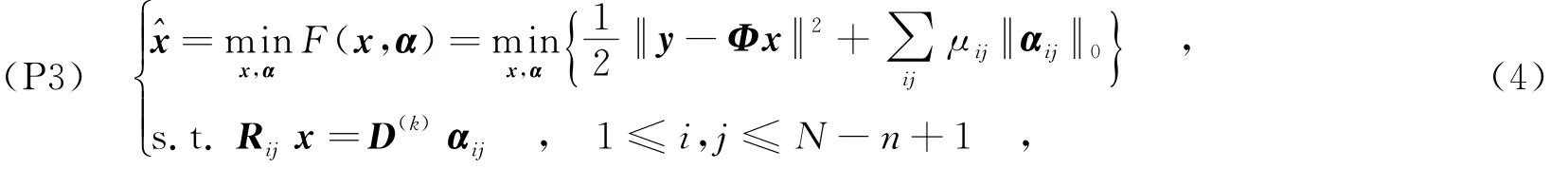
其中，α是全体分块的稀疏编码系数αij的集合.

2.2全变分正则化

根据以上分析，重建模型（P3）只利用了待重建图像在字典域下是稀疏的这一先验信息.正则化方法由于可以附加更多的约束条件，所以在求解反问题时可以获得更高的精度.全变分（Total Variation，TV）是根据自然图像的离散梯度具有稀疏性的先验知识提出来的一种有效的正则化约束模型，已成功应用于诸多图像处理的反问题中.根据全变分的定义，N×N的图像x有

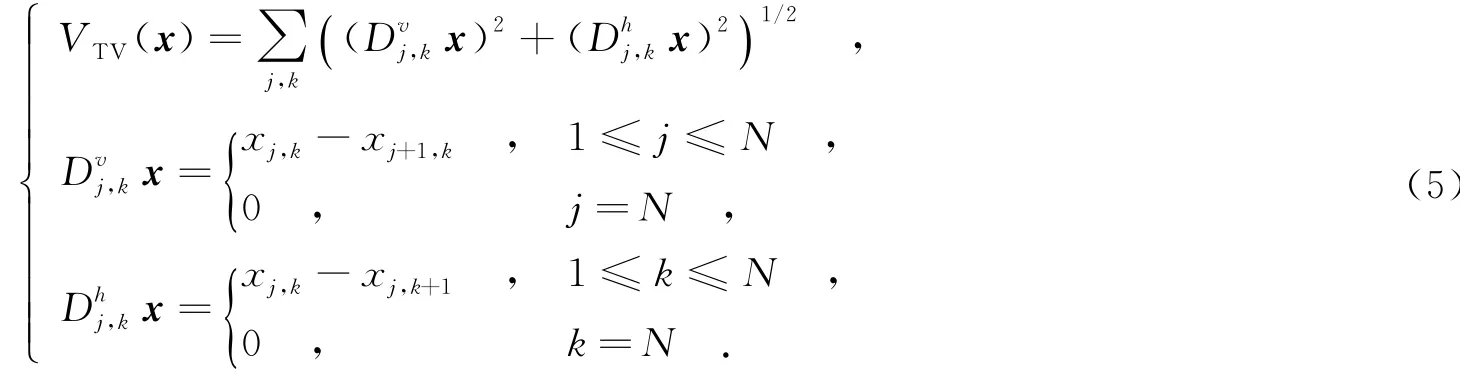
将图像的全变分VTV（x）作为正则化项加入到重建模型（P3）中，得到结合自适应稀疏表示和全变分约束的图像高分辨率重构模型（P4）:

其中，λ和μij（1≤i，j≤N-n+1）是正则化参数，α是全体分块在字典域下的稀疏编码系数αij的集合.

3 ASP-TV模型求解

最优化问题（P4）是一个带约束的多变量优化问题，无法直接求解.笔者结合Bregman迭代［12-13］的思想，将最优化问题（P4）分解为几个简单的子问题，然后通过分别求解各个子问题来求解问题（P4）.一般化最优化问题（P5）为其中，J（u）为凸函数，H（v）为可微的凸函数，Φ是线性算子.（P5）可以按照算法1所述的Bregman迭代算法来求解［13］.

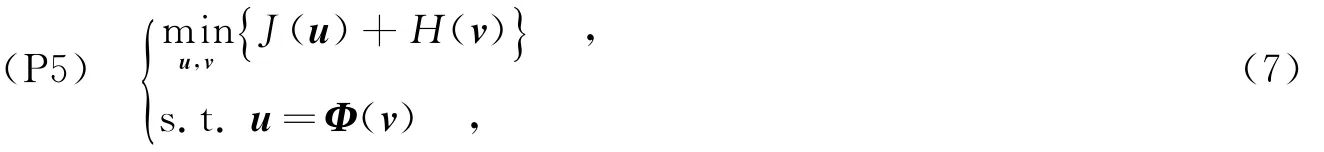
算法1 Bregman迭代算法.

步骤1 引入辅助变量b，初始化k=0，u（0）=0，v（0）=0，b（0）=0.

步骤2 判断是否收敛，若收敛，则执行步骤3；否则，执行如下迭代:

考虑到算法1中式（8）多变量优化问题的复杂性，采用分裂Bregman迭代（Split Bregman Iteration，SBI）方法［13］，得算法1步骤2中多变量优化问题的求解算法，如算法2所述.

算法2 分裂Bregman迭代算法.

步骤1 初始化，i=0，u（k+1，0）=u（k），v（k+1，0）=v（k）（u（k），v（k）是算法1中上一次的迭代结果），给出收敛判断条件.

步骤2 如果不收敛，则按下述步骤交替迭代:

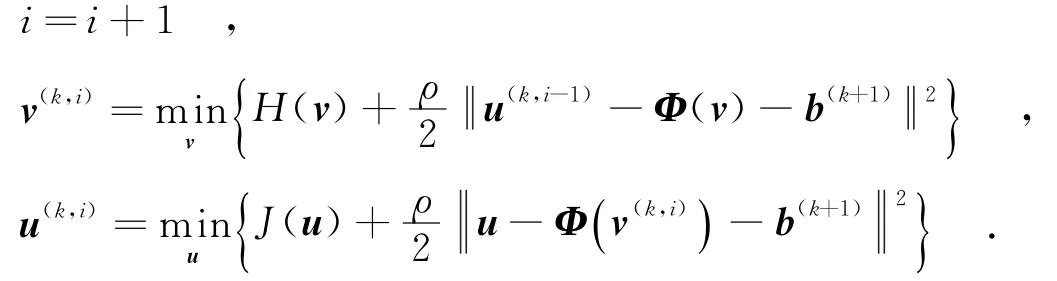
步骤3 将步骤2最终的交替迭代结果输出:（u（k+1），v（k+1））=（u（k，i），v（k，i））.根据前面分块的定义，待重建图像信号x与全体分块的稀疏编码系数的关系为

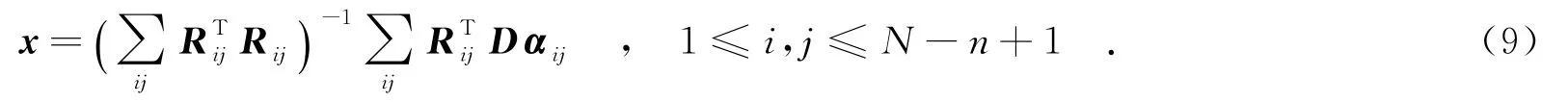
令

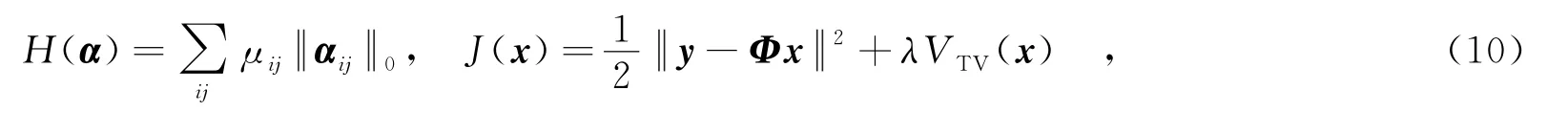
α是全体分块的稀疏编码系数的集合.显然，最优化问题（P4）是（P5）的一种情况.结合算法1和算法2得到求解结合自适应稀疏表示与全变分约束图像压缩感知的恢复模型（P4）的求解算法，如算法3所述.

算法3 恢复模型（P4）的求解算法.

步骤1 引入辅助变量b（b与图像x大小一致），初始化k=0，b（0）=0，根据部分采样数据反投影重建初始迭代图像x（0），确定收敛判定条件:前后两次迭代图像的差值图像的像素和占后一次迭代所获图像像素和的比小于10-5.

步骤2 计算图像x（k）与残差图像b（k）的差值图像x′（k）=x（k）-b（k），将x′（k）分块，采用K-SVD算法学习出字典D（k），并用正交匹配（Orthogonal Matching Pursuit，OMP）算法求解每个差值图像分块的稀疏编码:

步骤3 利用非线性共轭梯度法求解

步骤4 用步骤2所求稀疏编码系数重建出一幅图像，记为

步骤5 b（k+1）=b（k）+x′-x（k+1），k=k+1.

4 仿真实验与分析

为了说明笔者所提方法的有效性，从标准图像库中选取若干幅大小为256×256的典型测试图像，分别选择20%，30%，40%的采样率来进行重建实验.实验在处理器为Intel（R）Xeon E5-5503 CPU，2.30 GHz，内存为16 GB，操作系统为Windows XP（64 bit），环境为Matlab2012b的条件下进行.实验中，模型（P4）中参数λ选取0.005；参数μ在算法3步骤2中可以被吸收到参数ρ，参数ρ=0.15；图像稀疏编码时分块大小为8×8.根据部分采样数据，反投影重建一幅图像，以该图像为初始迭代图像，交替迭代，直至前后两次迭代图像的差值图像的像素和占后一次迭代图像像素和的比小于10-5.最后，将笔者提出的算法与当前几种不同类型的压缩感知重建图像算法分别从主观视觉和客观的峰值信噪比及特征相似度方面来比较.对比算法分别为分块压缩感知［15］、概率类算法贝叶斯压缩感知［16］、L1范数类算法GPSR［14］，稀疏变换均采用小波变换，参数均设置为默认参数.表1是各种算法在不同采样率下的峰值信噪比（Peak Signal to Noise Ratio，PSNR）和特征相似度（Feature SIMilarity，FSIM）的比较.其中，FSIM表示重建图像与原图的特征相似度，其值介于0到1之间，越大表示重建质量越好.限于篇幅，这里只列举了4幅典型图像的数据.

从表1的数值对比结果可知，对同一幅图像，在相同采样率下，笔者提出的算法框架与当前几种典型的图像压缩感知重建算法相比，不论是峰值信噪比还是特征相似度，都有一定程度的提高.重建质量的提高有两方面原因:一是稀疏编码阶段采用自适应冗余字典，而不是固定的字典或者完备正交变换，这对描述图像的细节具有重要意义.从对比中可以看到，像Barbara这种纹理细节丰富的图像，提高更明显.二是在稀疏优化问题求解时采用求解稀疏编码系数的近似L0范数的非凸优化问题，而对比算法分块压缩感知和梯度投影法都是求解稀疏编码系数的L1范数凸优化问题.由压缩感知基本理论可知，L0范数优化问题更接近真实解.为从视觉直观上进行比较，将对比算法与笔者提出的算法重建结果进行比较，由于篇幅所限，这里只列举了Barbara图像在视觉上的重建结果比较，如图2所示.

表1　不同算法的重建图像PSNR和FSlM比较

图2　实验比较结果

从图2中矩形标记的纹理部分可以看出，笔者提出的算法对图像纹理细节的重构明显好于对比算法.分块压缩感知和贝叶斯压缩感知在该部分都有明显的模糊块状.GPSR算法虽然在纹理部分的效果较分块压缩感知和贝叶斯压缩感知方法的都有一定的提高，但在图像平滑部分却引入了较多的类似椒盐噪声的斑点，所以整体效果差于上述两种算法.由于笔者提出的算法中引入了全变分约束，所以对图像的平滑部分的重建比其他几种算法效果要好，从图中Barbara手臂的重建效果对比可以看出这种优势.

5 结束语

相对于传统图像压缩感知中以完备正交基作为稀疏变换基，笔者提出了采用自适应冗余字典作为信号的稀疏变换基，并通过加入总变分正则化项，得到了ASP-TV的高分辨率图像重建模型.仿真实验表明，这种算法能够在低采样率下重建出高质量的图像.由于在求解稀疏优化问题时，笔者采用了共轭梯度法，涉及到矩阵求逆及矩阵乘法问题，当图像的维度较大时，对处理器和存储器的要求较高.另外，在图像恢复模型中只利用了稀疏先验知识，忽略了稀疏系数的结构信息.挖掘更多的先验约束能够提高重建的精度，在稀疏先验的基础上，利用贝叶斯方法对稀疏系数分布进行建模，可以进一步提高重建图像的精度.

［1］DONOHO D L.Compressed Sensing［J］.IEEE Transactions on Information Theory，2006，52（4）:1289-1306.

［2］ZHAN X，ZHANG R，YIN D，et al.SAR Image Compression Using Multiscale Dictionary Learning and Sparse Representation ［J］.IEEE Geoscience and Remote Sensing Letters，2013，10（5）:1090-1094.

［3］MA L Y，MOISAN L，YU J，et al.A Dictionary Learning Approach for Poisson Image Deblurring［J］.IEEE Transactions on Medical Imaging，2013，32（7）:1277-1289.

［4］王良君，石光明，李甫，等.多稀疏空间下的压缩感知图像重构［J］.西安电子科技大学学报，2013，40（3）:73-80. WANG Liangjun，SHI Guangming，LI Fu，et al.Compressed Sensing Image Reconstruction in Multiple Sparse Spaces ［J］.Journal of Xidian University，2013，40（3）:73-80.

［5］HUANG H J，YU J，SUN W D.Superresolution Mapping Using Multiple Dictionaries by Sparse Representation［J］. IEEE Geoscience and Remote Sensing Letters，2014，11（12）:2055-2059.

［6］HUANG D A，KANG L W，CHIANG Y，et al.Self-learning Based Image Decomposition with Applications to Single Image Denoising［J］.IEEE Transactions on Multimedia，2014，16（1）:83-93.

［7］YANG M，ZHANG L，FENG X C，et al.Sparse Representation Based Fisher Discrimination Dictionary Learning for Image Classification［J］.International Journal of Computer Vision，2014，109（3）:209-232.

［8］许建楼，冯象初，郝岩.二阶总广义变分图像修复模型及其算法［J］.西安电子科技大学学报，2012，39（5）:18-23. XU Jianlou，FENG Xiangchu，HAO Yan.Second Order Total Generalized Variational Inpainting model and Its Algorithm［J］.Journal of Xidian University，2012，39（5）:18-23.

［9］练秋生，周婷.结合字典稀疏表示和非局部相似性的自适应压缩成像算法［J］.电子学报，2012，40（7）:1416-1422. LIAN Qiusheng，ZHOU Ting.Adaptive Compressed Imaging Algorithm Combined the Sparse Representation in the Dictionaries with Non-Local Similarity［J］.Acta Electronica Sinica，2012，40（7）:1416-1422.

［10］DONG W，ZHANG L，SHI G，et al.Nonlocally Centralized Sparse Representation for Image Restoration［J］.IEEE Transactions on Image Processing，2013，22（4）:1620-1630.

［11］AHARON M，ELAD M，BRUCKSTEIN A.K-SVD:An Algorithm for Designing Overcomplete Dictionaries for Sparse Representation［J］.IEEE Transactions on Signal Processing，2006，54（11）:4311-4322.

［12］GOLDSTEIN T，OSHER S.The Split Bregman method for L1 regularized problems［J］.SIAM Journal of Imaging Sciences，2009，2（2）:323-343.

［13］YIN W，OSHER S，GOLDFARB D，et al.Bragman Iterative Algorithms for L1-Regularization with Application to Compressed Sensing［J］.SIAM Journal of Imaging Sciences，2008，1（1）:143-168.

［14］FIGUEIREDO M A T，NOUAK R D，WRIGHT S J.Gradient Projection for Sparse Reconstruction:Application to Compressed Sensing and Other Inverse Problems［J］.IEEE Journal of Selected Topics in Signal Processing，2007，1（4）: 586-597.

［15］FOWLER J E，MUN S，TRAMEL E W.Multiscale Block Compressed Sensing with Smoothed Projected Landweber Reconstruction［C］//European Signal Processing Conference.Poland:EUSIPCO，2011:564-568.

［16］JI S H，XUE Y，CARIN L.Bayesian Compressive Sensing［J］.IEEE Transactions on Signal Processing，2008，56（6）: 2346-2356.

（编辑:郭 华）

Adaptive sparse representation and total variation constraint based image reconstruction

WANG Yong1，FENG Tangzhi1，CHEN Chuchu1，QIAO Qianqian1，YANG Xiaoyu1，WANG Guodong1，GAO Quanxue2
（1.School of Electronic Engineering，Xidian Univ.，Xi’an 710071，China；2.School of Telecommunication Engineering，Xidian Univ.，Xi’an 710071，China）

In view of the limitation of fixed complete orthogonal transformation，represented by twodimensional wavelet transform and discrete cosine transform in compressed sensing high-resolution image reconstruction，this paper proposes a new method for high-resolution image reconstruction based on adaptive redundant dictionary sparse representation with the total variation constraint.The algorithm takes the intermediate image in the process of iteration as the training sample to get a redundant dictionary suitable for sample characteristics by adaptive learning.It makes full use of the correlation between dictionary atoms and the image to get an ideal complete sparse representation，thus reducing the sampling rate and improving the quality of image reconstruction.Finally，the algorithm takes the total variation as a constraint and uses the split Bregman iterative method to solve the sparse optimization problem.Simulation shows that the proposed method can reconstruct high quality images under a low sampling rate.

compressed sensing；adaptive redundant dictionary；sparse representation；image reconstruction；total variation

TN911.73

A

1001-2400（2016）01-0012-06

10.3969/j.issn.1001-2400.2016.01.003

2014-07-29 网络出版时间：2015-04-14

国家自然科学基金资助项目（61271296）；中央高校基本科研业务费专项资金资助项目（JB150218）；西安电子科技大学教育教学改革研究资助项目（B1311）；西安电子科技大学新实验开发与新实验设备研制及实验教学改革资助项目（SY1354）

王 勇（1976-），男，副教授，E-mail:yongwang@126.com.

网络出版地址：http://www.cnki.net/kcms/detail/61.1076.TN.20150414.2046.003.html