基于“数学实验”下的“均值不等式”教学与思考
2016-09-12浙江省象山县职业高级中学
☉浙江省象山县职业高级中学 郑 琰
教材教法
基于“数学实验”下的“均值不等式”教学与思考
☉浙江省象山县职业高级中学 郑 琰
数学知识具有较强的抽象性,这造成了数学难懂、难教、难学,乃至于谈“数”色变.能否像物理实验、化学实验那样,让形式化的数学在“实验”过程中变得“可视化”,这便是“数学实验”的起点与归宿.
“数学实验”是通过动手动脑“做”数学的一种数学学习活动,是学生运用有关工具(如纸张、剪刀、模型、测量工具、作图工具及计算机等),在数学目标的指导下进行的一种以实际操作为主要特征的数学验证或探究活动.其目的是让学生在活动中直观形象地看清数学知识,并逐步对其适度抽象,进行更高层次上的“再实验”.“数学实验”可以培养学生的理性思维,提高实践能力和创新精神,这正是新课标所倡导的数学素养和数学的人文价值之所在.
“数学实验”在职高的数学学习中已被广泛地接受和运用,在普通高中情况如何呢?笔者以“均值不等式”为载体,在普通高中学生中作了一次体验,现总结和思考如下,供同行参考.
一、“数学实验”下的教学过程
环节1:模拟生活实际引出课题
一年轻人去金店买项链,但电子秤坏了,只有一个断了一臂并用绳子捆住的天平(图1),不知咋办.于是,店主提议:先将项链置于左盘,砝码置于右盘,平衡时读得砝码为a,再将项链与砝码交换,平衡时读得砝码为b.最后以作为项链重量卖给小伙子.假如是你去买,你同意这个方案吗?

图1
事实上,设项链的重量为x,天平左右两臂的长度分别为l1和l2,则由杠杆原理有两式相乘可得x=,这样,问题就转化为比较与的大小了.
效能分析:数学应用的广泛性是数学的基本特征,以实际问题引出课题,让学生在感悟数学应用价值的同时,更能激发学生的好奇性和学习数学的积极性.
环节2:尝试用线段(一维空间)构建几何模型
在一维空间中,a、b可以用线段的长度来表示,不妨设AD=a,DB=b,于是,问题指向于可以用怎样的线段来表示?结合初中学过的射影定理(直角三角形中,斜边上的高是两直角边在斜边上射影的比例中项),把AD、DB作为两直角边在斜边AB上的射影,这样构建的Rt△ABC(∠C=90°),其斜边上的高CD=(图2).

图2
即对于a,b∈R+,恒有≥,当且仅当a=b时,等号成立.
效能分析:利用线段比长短是学生最容易想到的方法.教学中,笔者进一步作出Rt△ABC的外接圆O,并延长CD交圆O于点E(图3),则AB=a+b,CE=2.于是,“均值不等式”便有了自己的几何解释——在一个圆内,任何半弦长不大于半经.

图3
环节3:尝试用面积(二维空间)构建几何模型
模型1:将a表示为正方形ABCD的面积,b表示为正方形AB′C′D′的面积,则就是以上两个正方形的两边AD和AB′为边长的长方形AB′ED的面积,将这三个图形以角A重合为标准叠合在一起(图4).显然S△ACD+S△AB′C′=,S长方形AB′ED=.因为两个三角形的面积之和大于
的边长相等,即a=b时取等号.

图4

图5
在图5④中,四个直角三角形的面积为S△=2,正方形BDEF的面积为S正方形BDEF=a+b,于是有a+b≥2即,当且仅当长方形ABCD为正方形时,即a= b时取等号.

图6
观察图4,△CEC′的面积就是“均值不等式”两边的差量,即这给不等式的代数证明提供了启示,同时也给不等式两端到底相差多少给出了几何注释.通过几何直观,不仅比较了两者的大小,还能加深对均值不等式的深层理解.
环节4:尝试用二元函数(三维空间)构建几何模型
从图7中不难发现,平面总是在曲面的上方,也就是说对于任意的x,y∈R+,都有(fx,y)≥g(x,y),即成立.
效能分析:信息技术正在改变着人们的生活方式、学习方式和工作方式,也改变着传统的数学教育方式.通过3D技术的智能论证,既活跃了课堂教学形式,也展现了数学学习的新方式.
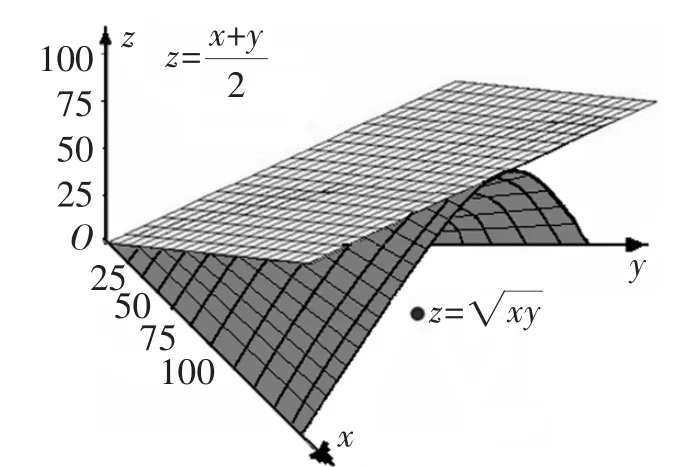
图7
环节5:尝试用代数方法证明不等式
在a,b∈R+的条件下,要证,只要证a+b≥,只要证a+b-2,只要证()2≥ 0,显然上式是成立的,当且仅当a=b时取等号.
效能分析:强调“均值不等式”的代数证明,还是要体现数学的严谨性.同时,观察图5,正方形GHIJ的面积等于()2,这也是上述代数证明的最终归属,至此,几何与代数虽方法迥异,但殊途同归,两者相得益彰.
二、“数学实验”后的教学思考
课后,教研部门组织了部分教师、学生对此作了研讨、评价,结论褒贬不一.学生普遍呈雀跃状,不同的学习方式极大地提升了学生的学习兴趣,课堂参与率很高,对所学的知识理解深刻.教师多数抱担忧形,本来几分钟就能解决的“均值不等式”竟花费一节课,课堂效率何在,高考题目咋解?作为当事人,笔者也有几点思考:
1.“数学实验”是课程标准的一贯坚持
关于“数学实验”,《义务教育数学课程标准(2011年年版)》首先提出了“学生应当有足够的时间和空间经历观察、实验、猜测、计算、推理、验证等活动过程”,明确了“动手实践也是数学学习的一种重要方式”.并要求“有条件的学校可以建立‘数学实验室’供学生使用,以拓宽他们的学习领域,培养他们的实践能力,发展其个性品质与创新精神”.《普通高中数学课程标准(实验)》则进一步提出“学生的数学学习活动不应只限于接受、记忆、模仿和练习,高中数学课程还应倡导自主探索、动手实践、合作交流、阅读自学等学习数学的方式”,并强调“这些方式有助于发挥学生学习的主动性,使学生的学习过程成为在教师引导下的‘再创造’过程”.同时,普通高中数学课程还设立了“数学探究”、“数学建模”等学习活动,其目的是“为学生形成积极主动的、多样的学习方式进一步创造有利的条件,以激发学生的数学学习兴趣”.由此可见,数学课程标准,无论是义务阶段还是高中阶段,对数学教学的方法手段都提出了新的要求,“数学实验”正是新课程所倡导的积极主动、勇于探索的学习方式之一.通过构建“做”数学的教学环境,开展数学实验教学,使学生的数学潜能得到最大的开发,是数学课程标准的一贯坚持.
2.“数学实验”是课程理念的具体体现
课程基本理念强调高中数学教学要返璞归真,努力揭示数学概念、法则、结论的发现过程和本质.要通过典型例子的分析和自主探索活动,使学生理解数学概念、结论逐步形成的过程,体会蕴含其中的思想方法,追寻数学发展的历史足迹,把数学的学术形态转化为学生易于接受的教育形态.依据课程理念,人教版数学课程也安排了“探究与发现”、“实习与思考”等小栏目,为教师开展“数学实验”提供素材和基本线索.数学家弗赖登塔尔在20世纪就说过“要实现真正的数学教育,必须从根本上以不同的方式组织教学,否则是不可能的.它要求有个实验室,学生在那里可以个别活动或是小组活动”.[4]因此,根据具体的教学内容,适当开展数学实验教学活动,让学生去观察、分析实验现象,从中获得数学的基础知识、基本技能、基本思想和基本活动经验,是实现真正的数学教育的企求,也是高中数学课程理念的具体体现.
3.“数学实验”不分普通高中与职业高中
有研究表明,高中学生的认知水平处于由直观感知到描述抽象的演变期,思维水平处于直觉经验思维向逻辑推理思维的过渡期,他们对概念的理解、判断和推理很大程度上还离不开直观形象的实物支撑.而“实验教学”注重实测和直观,具有可操作性和实践性,能有效地促进学生的数学学习.在高中数学教学中开展实验教学,将抽象的数学概念“可视化”,符合学生的认知水平和思维特点,无疑能激发学生的学习兴趣,使学生逐步学会数学思维的物质实践方法,掌握数学研究规律,形成理性思维.另一方面,高中学生年龄还决定了他们好奇、好动,喜欢富有挑战性的特点.因此,开展数学实验教学,让学生通过操作、实践、实验,既满足学生的天性,又培养学生的动手能力、思维能力.“数学实验”其实就是一个科学研究的过程、探索真理的过程.通过“各种不同形式的自主学习、探索活动,让学生体验数学发现和创造的历程,发展他们的创新意识”不分普通高中还是职业高中.
4.“数学实验”想说爱你不容易
长期以来,普高老师处于“好心”,为了节约时间,追求“高效率”,把教材中的知识嚼细后喂给学生.教师的讲授替代了学生的学习、替代了学生的思维过程,使学生丧失了独立思考、自主探索的机会.导致大部分学生只会对着题型套路解题,而在面对新的问题时则茫然不知所措.在数学实验教学过程中,离开教师的指导和提示,多数学生很难开展独立的实验.此外,针对不同的教学内容,如何构建实验素材,如何理清数学实验与高考解题的关系,如何转变教师的教育观念等问题也困扰着数学实验的开展.
总之,“数学实验”还有很长的路要走,“数学实验”想说爱你不容易.
1.刘绍学.普通高中课程标准实验教科书·数学(必修5)A版[M].北京:人民教育出版社,2015.
2.中华人民共和国教育部制定.义务教育数学课程标准(2011年版)[M].北京:北京师范大学出版社,2012.
3.中华人民共和国教育部.普通高中数学课程标准(实验)[M].北京:人民教育出版社,2003.
4.弗赖登塔尔,著.作为教育任务的数学[M].陈昌平,唐瑞芬,译.上海:上海教育出版社,1995.F
