一种用于室内定位的线性规划算法*

徐　琨，刘宏立，马子骥，胡久松

(湖南大学 电气与信息工程学院,湖南 长沙　410082)



一种用于室内定位的线性规划算法*

徐琨，刘宏立†，马子骥，胡久松

(湖南大学 电气与信息工程学院,湖南 长沙410082)

针对基于ToA定位中存在的信标节点较少和发送时间不能提前预知的问题，提出了一种新的应用于无线传感网络室内定位的线性规划算法.通过考虑测量值的最小平均绝对值误差，利用线性逼近方法，将一个复杂的、非凸的室内定位问题转换为一个简单的线性规划问题，并用迭代求精的方法求出最优解.仿真结果表明，提出算法计算复杂度低，收敛速度快，可以快速地求出未知节点的坐标；通过和已有的定位算法相比，提出算法在信标节点较少的情况下，仍能保持很好的定位精度，利用较少的节点资源达到比已有算法更好的定位性能.

无线传感器网络；到达时间；定位；线性规划；迭代

目前，随着无线通信技术、嵌入式技术和网络技术的快速发展，无线传感网络[1](Wireless Sensor Networks，WSN)得到了前所未有的关注，已经成为研究热点.定位技术[2]是WSN中最重要的基础性研究之一，没有位置信息的WSN应用是没有任何意义的.基于WSN的定位是根据不同定位技术的测量值来确定网络中传感节点的位置，常采用的定位技术主要有基于到达时间[3](Time of Arrival，ToA)的定位，基于到达时间差[4](Time Different of Arrival，TDoA)的定位，基于到达角度[5](Angle of Arrival，AoA)的定位和基于接收信号强度[6](Received Signal Strength Indicator，RSSI)的定位等.基于WSN的定位系统被广泛用于各种实际应用中，如环境监测[7]、工业自动化过程控制[8]和家庭医疗保健[9]等.

基于ToA的定位技术具有定位精度高、实现简单等优点，得到了国内外研究者的广泛关注，目前已有很多基于ToA的定位研究方法.最大似然估计方法[10](Maximum Likelihood，ML)是最常用的方法之一，但是，要得到基于ToA定位问题的最大似然估计量是一个困难的全局优化问题.很多研究者提出了一些替代方法来避免复杂的全局优化问题，文献[11]将定位问题转换成一个半正定规划松弛问题(Semidefinite Programming Relaxation，SDP)进行求解，通过采用解决SDP的方法来降低求解ML问题的复杂度.文献[12]提出用线性最小二乘法(Linear Least Square，LLS)解决定位问题.通过这个方法，能够在测量噪声较小的情况下得到较好的定位性能.文献[13]基于极小极大方法，提出了2个次优的方案来解决定位问题,虽然已经提出了很多有效的方法能够减少基于ToA的定位问题的复杂度和得到较好的定位精度，但是它们基本上都要求部署较多的信标节点和提前知道信号的发送时间，没有考虑信标节点较少和发送时间未知的情况.

在实际应用中，不可能在一个区域内部署大量的信标节点，而且这些信标节点也基本上不能提前知道目标节点发送信号的初始时间.本文针对信标节点部署较少、发送时间未知的情况，提出了一种新的基于线性规划的定位优化算法,通过多个信标节点接收到的ToA测量值，消除发送时间未知对定位的影响；考虑残差的最小平均绝对值误差，将一个原始形式为非凸优化的定位问题转换成线性规划问题(Linear Programming，LP).线性规划结构简单，计算复杂度低，可以采用迭代求精的方法快速求出最优解，得到未知节点的坐标.仿真结果证明了提出的算法具有很好的定位性能，特别是在信标节点较少的情况下，提出算法的定位性能明显优于已有的定位算法.

1　系统模型

考虑二维空间R2中,一个由m个信标节点P和n个未知节点U组成的无线传感网络，每个信标节点的位置已知，其坐标为pi=(xi,yi)T∈R2,i=1,2,…,m；每个未知节点的位置未知，其坐标为ui∈R2,i=1,2,…,n.某个未知节点u=(x,y)在时间点T广播一个无线信号给网络中所有的传感节点，其中有k个信标节点接收到了未知节点u发送的无线信号.信标节点事先不知道发送时间T的大小，即目标节点发送信号的时间t0未知.可以将每个信标节点接收到的ToA测量值用数学模型表示为:

ti=t0+di/v+ωi,i=1,2,…,k.

(1)

由于未知节点的发送时间和位置不确定，式(1)中的t0和未知节点的坐标都是未知变量.因为存在多个未知变量，要求出式(1)中的所有未知变量的解是非常困难的，具有较高的计算复杂度.当未知节点向网络中的所有节点广播无线信号时，虽然发送信号的时间并不确定，但是会有多个信标节点接收到这个发送时间点所发送的无线信号，因此，为了减少计算的复杂度，提高定位的效率，可以根据不同信标节点得到的测量值，消除发送时间t0对定位的影响.通过将式(1)中的前k-1个等式分别减去第k个等式，可以得到一个只包含未知节点坐标为未知变量的k-1项不等式组，其表示形式为：

(2)

将式(2)用向量可以表示为：

ti-tk=di/v+ωi-dk/v-ωk;

i=1,2,…,k-1.

(3)

将式(3)进行整理，可以简化为：

R=D+X.

(4)

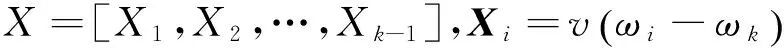
(5)

式(5)表示一个非线性、非凸的优化问题，要求出该问题的最优解是一个复杂的全局优化问题，接下来，我们提出一种基于线性规划的优化算法来解决这个问题.

2　基于LP的定位算法

对于式(5)所描述的定位问题，它表示一个非凸的优化问题，求解过程非常复杂，很难求出对应的全局最优解，可以将其等价地表示为以下形式:

(6)

通过等价变换，将复杂的定位问题转化为一个带约束条件的优化问题.但是在式(6)所表示的优化问题中，虽然目标函数是线性的，但是约束条件中存在平方根，其表示的优化问题仍然是一个非凸非线性的优化问题，对其进行求解是一件很困难的事情.而且，由于是一个非凸的优化问题，在对其进行求解的过程中，求出的最优解可能只是局部最优解，而不能得到优化问题的全局最优解.为了消除式(6)中的非线性项，通过采用线性逼近的方法，从问题域中选取一个点ul，将约束条件中的非线性项‖u-pi‖2围绕着点ul进行一阶泰勒逼近，使其转化为线性项.

‖u-pi‖2≃‖ul-pi‖2+

(7)

式中：ul为初始值；(·)表示在位置ul处的梯度，.将式(7)代入式(6)，通过化简可以得到：

(8)

其中：

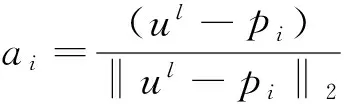
(9)

ci=ri-‖ul-pi‖2+aiul.

(10)

通过采用松弛技术，将式(8)所描述的问题表示成一个二阶锥规划的形式，通过求解二阶锥规划的方法进行求解.但是，由于在约束条件中还存在非线性项，其对应的求解过程依然比较复杂，可以将式(8)所描述的问题进一步进行优化，通过继续采用一阶泰勒逼近，可以将约束条件中的非线性项继续近似表示成线性形式，通过整理，可以表示为：

(11)

其中:

Ai=ak-ai;

(12)

Ci=‖ul-pk‖2-akul+ci.

(13)

通过两次线性逼近方法，约束条件中的所有非线性项都已经被转化成线性形式.从式(11)可以看出，它表示一个典型的线性规划问题,可以很容易地对其进行求解，求出的最优解即是全局最优解，获得目标节点的位置信息，而且计算复杂度低.

3　性能分析

为了验证提出的LP定位算法的性能，基于一个室内环境进行计算仿真，并跟已有的LLS算法和SDR算法进行比较.我们利用Matlab CVX工具来求解提出的LP算法和SDR算法.考虑一个由9个信标节点和一个目标节点组成的传感网络，将目标节点和信标节点部署在一个100 m×100 m的二维空间内，预先部署一些信标节点，它们的坐标分别是p1=[0,0]，p2=[0,50]，p3=[0,100]，p4=[50,0]，p5=[50,50]，p6=[50,100]，p7=[100,0]，p8=[100,50]，p9=[100,100]，目标节点随机部署在定位区域内.对于3种不同的定位算法，设每个节点测量噪声的标准差相同，即σi=σ (i=1,…,m).对3种算法进行仿真，每次进行100次实验取其平均值.

在不同的测量噪声影响下，定位算法会有不同的定位精度，不同测量噪声值下的定位精度如图1所示.

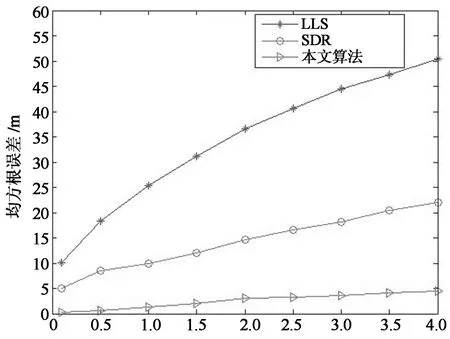
测量噪声标准差σ/m

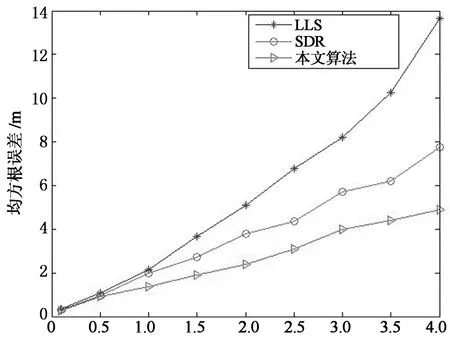
测量噪声标准差σ/m

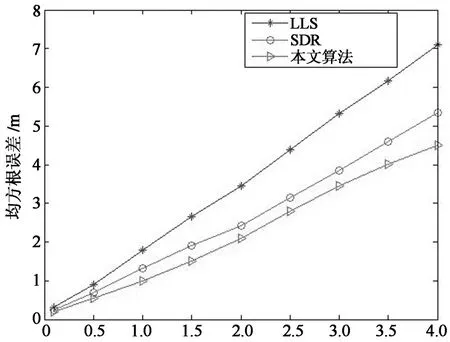
测量噪声标准差σ/m

从图1可以看出，在不同的测量噪声和信标节点个数下，提出算法要明显优于LLS算法，具有和SDR算法相似的定位精度.不管部署多少个信标节点，当测量噪声较小时，3种不同的定位算法都能得到较好的定位性能，但随着测量噪声的增大，3种定位算法的定位误差也会跟着提高，信标节点部署较多时，定位误差增长的程度会降低，其中，LLS算法的定位误差增加的程度最为明显.当信标节点个数较少时，即使在测量噪声很小的情况下，LLS算法和SDR算法依然具有较高的定位误差,本文提出算法明显优于LLS算法和SDR算法.

不同信标节点个数对定位精度也有影响，图2表示了测量噪声标准差σ=2 m的情况下，不同算法的定位精度随信标节点个数的影响.由图2可知，随着信标节点的增多，3种定位算法的定位精度都会得到提高，其中，LLS算法受信标节点个数的影响最大，当信标节点个数增加到一定程度后，对定位精度的影响会慢慢趋于饱和.当部署的信标节点较少时，提出算法依然能够得到较好的定位性能，远远胜过LLS算法和SDR算法的定位精度，其中，LLS算法的定位误差最大.

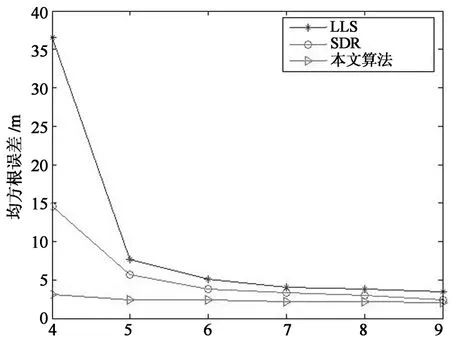
信标节点个数

对于提出算法，需要计算式(5)中平均绝对值误差‖R-D‖1的值.设R-D=e，随机选择一个初始点u0，通过仿真可以计算出算法的收敛速度.设迭代次数为10，重复运行算法10次.其平均绝对值误差和收敛性之间关系如图3所示.图3表示在有4个信标节点，测量噪声标准差为2 m的情况下，提出算法完成一次定位运算的收敛速度，可以很清楚地看到，提出算法在信标节点较少的情况下，收敛速度非常快，只需要3次迭代就收敛了.

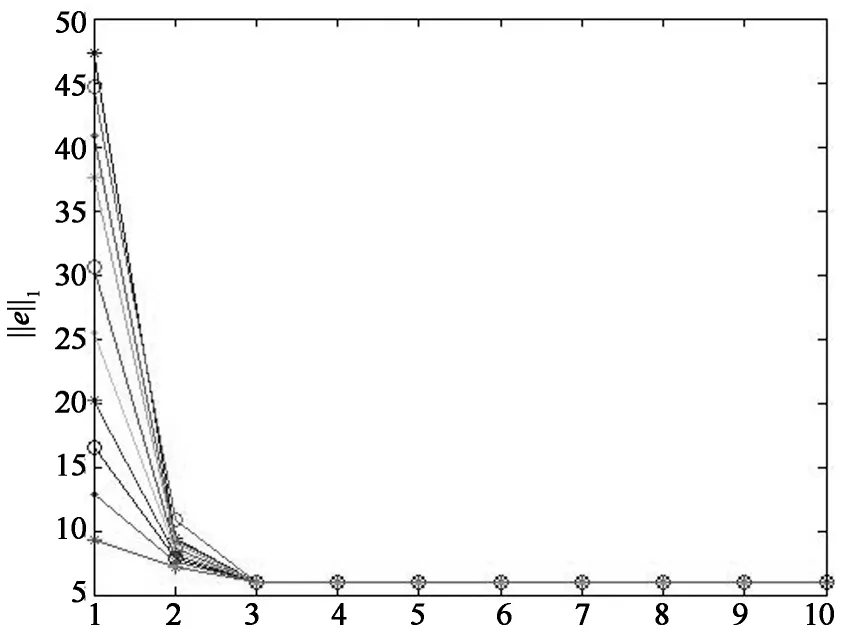
迭代次数

4　结　论

针对基于ToA定位中存在的信标节点少和发送时间不能提前预知的问题，提出了一种新的解决室内定位的线性规划算法，通过提出的算法，可以快速有效地解决目标节点的定位问题.计算仿真表明，本文提出的算法具有较好的定位性能，尤其在信标节点较少的情况下，提出算法明显优于已有的定位算法.

[1]CHIARA B,ANDREA C,DAVIDE D,etal.An overview on wireless sensor networks technology and evolution[J].Sensors, 2009, 9(9):6869-6896.

[2]CONTI M,WILLEMSEN J,CRISPO B.Providing source location privacy in wireless sensor networks: a survey[J]. IEEE Communications Surveys and Tutorials,2013,15(3):1238-1280.

[3]HUANG J, XUE Y, YANG L. An efficient closed-form solution for joint synchronization and localization using ToA[J]. Future Generation Computer Systems,2013,29(3):776-781.

[4]GHOLAMI M R,GEZICI S,STROM E G.TDOA based positioning in the presence of unknown clock skew[J].IEEE Transactions on Communications, 2013,61(6):2522-2534.

[5]MALAJNER M,PLANINSIC P,GLEICH D.Angle of arrival estimation using RSSI and omnidirectional rotatable antennas[J].IEEE Sensors Journal, 2012,12(6):1950-1957.

[6]SAHU P K,WU E H K,SAHOO J.DURT: Dual RSSI trend based localization for wireless sensor networks[J].IEEE Sensors Journal,2013, 13(8):3115-3123.

[7]ZHAO J,XI W,HE Y,etal.Localization of wireless sensor networks in the wild:pursuit of ranging quality[J].IEEE/ACM Transactions on Networking, 2013,21(1):311-323.

[8]RAWAT A S,ANAND P,CHEN H,etal.Collaborative spectrum sensing in the presence of Byzantine attacks in cognitive radio networks[J]. IEEE Transactions on Signal Processing,2011,59(2):774-786.

[9]LI K J,BIGHAM J,BODANESE E L,etal.Outdoor location estimation in changeable environments[J].IEEE Communications Letters,2013,17(11): 2072-2075.

[10]MOHAMMAD R G,SINAN G,ERIK G S.Improved position estimation using hybrid tw-ToA and TDoA in cooperative networks[J]. IEEE Transactions on Signal Processing, 2012,60(7):3770-3785.

[11]WANG G, LI Y M, WANG R D. New semidefinite relaxation method for acoustic energy-based source localization[J].IEEE Sensor Journal,2013, 13(5):1514-1521.

[12]YANG L,HO K C.An approximately efficient TDoA localization algorithm in closed-form for locating multiple disjoint sources with erroneous sensor positions[J].IEEE Transactions on Signal Processing,2009,57(12):4598-4615.

[13]XU E,DING Z,DASGUPTA S.Reduced complexity semidefinite relaxation algorithms for source localization based on time difference of arrival[J].IEEE Transactions on Mobile Comput,2011,10(9):1276-1282.

A Linear Programming Algorithm for Indoor Localization in Wireless Sensor Networks

XU Kun, LIU Hong-li†, MA Zi-ji, HU Jiu-song

(College of Electrical and Information Engineering, Hunan Univ, Changsha, Hunan 410082, China )

To solve the problem of fewer beacon nodes and unknown transmission time in Time of Arrival (ToA) based localization, a new linear programming algorithm was proposed to approximate nonlinear localization estimation problems. We consider the least-mean absolute errors of the residual and formulate the nonconvex localization problem as a simple linear programming by using linear approximation. Simulation results demonstrate that the proposed algorithm can maintain good positioning accuracy under fewer beacon nodes and achieve better performance by using less node resources than the existing algorithms.

wireless sensor networks;time of arrival;localization;linear programming;iteration

1674-2974(2016)08-0115-05

2015-06-03

国家自然科学基金资助项目(61172089), National Natural Science Foundation of China(61172089)；中央国有资本经营预算支出项目(财企[2013]470号)；中国博士后科学基金资助项目(2014M562100)；湖南省科技厅资助项目(2014WK3001)

徐琨(1979-)，男，湖南津市人，湖南大学博士研究生，高级工程师†通讯联系人，E-mail:hongliliu@hnu.edu.cn

TP393

A