机械系统可靠性定量评价方法

高　鹏，谢里阳（.辽宁石油化工大学机械工程学院，辽宁 抚顺 300；.东北大学航空动力装备振动及控制教育部重点实验室，沈阳 089）

机械系统可靠性定量评价方法

高鹏1，谢里阳2
（1.辽宁石油化工大学机械工程学院，辽宁 抚顺 113001；
2.东北大学航空动力装备振动及控制教育部重点实验室，沈阳 110819）

随着机械产品结构和工作环境日益复杂，机械系统可靠性的正确评估对产品质量评价和全寿命周期管理具有重要的现实意义。简要介绍机械可靠性定量模型的建模原理、研究现状和存在的问题，指出尽管静态系统可靠性模型相对成熟，对传统应力强度干涉模型进行扩展可解决大部分机械零部件及机械系统的可靠性评估问题，但是，当机械零部件强度退化时，机械系统可靠性分析需要考虑时间因素，传统静态模型无法满足时变可靠性分析要求。因此，着重阐述了机械系统时变可靠性模型建模过程中有待解决的关键问题。

可靠性；机械系统；失效率；干涉模型

0　引言

自第二次世界大战后可靠性工程兴起以来，国内外研究人员对电子、机械等不同工程系统的可靠性评价进行了大量且卓有成效的理论和实践研究。就机械系统而言，其工作环境与结构功能日益复杂，在设计、制造和使用等环节存在大量影响可靠性的随机因素。随着对机械产品可靠性与安全性要求的提高，机械系统可靠性的精确评估方法面临着新的挑战。

目前，以故障模式影响及危害性分析（FMECA）和故障树分析（FTA）方法为代表的半定性可靠性模型取得了较大的进展。这些模型由于操作简单，便于实现工程师经验与管理人员目标的有效统一而广泛应用于工程实际。然而，在系统全寿命可靠度精确表征、系统稳健性分析以及系统优化设计等方面，由于定性模型在分析指标量化方面的不足，需要进一步展开可靠性定量模型的深入研究。机械系统可靠性定量研究起步相对较晚，大多沿用电子系统的可靠性计算方法。这些方法通常以失效率作为零件和系统可靠性评价的基本输入参数。但是，失效率由于对载荷和材料等随机因素具有较强的敏感性，其统计和验证工作对于机械系统而言较为困难，甚至无法实现。此外，机械工程师更关注的是与机械产品设计和制造相关的载荷和机械性能等参数的随机特性对可靠性的直接影响。因此，在系统可靠性建模过程中，如何以这些参数作为基本输入并考虑系统失效机理来构建机械系统可靠性定量模型，是需要进一步研究的重要问题。本研究将在简要介绍现有定量机械可靠性模型研究现状的基础上，指出建模中需要解决的问题。

1　静态机械系统可靠性定量分析模型

传统机械可靠性定量分析多直接引用电子系统可靠性模型。但是，正如Moss所指出，虽然研究人员对电子元器件及系统的评估方法做了大量的研究，但是由于机械产品与电子产品在工作方式和失效模式等方面存在着本质的区别，这些可靠性分析方法被应用于机械系统时应该引起足够的注意［1］。Freudenthal于1947年提出了著名的应力-强度干涉（SSI）模型［2］。该模型以应力和强度的随机分布为输入，完成机械零部件可靠性的定量评价，并通过系统结构函数进一步计算机械系统可靠度。相对于其他以失效率为输入变量的可靠性模型，以SSI模型为基础的系统可靠性建模方法由于可以综合考虑系统中零部件在设计、制造过程中存在的各种随机因素，并且便于通过试验获得应力和强度的统计特征，因此得到广泛应用，并成为目前机械系统可靠性定量分析的重要理论基础。当应力与强度的分布函数分别需要由多个随机变量（如零件的尺寸）共同确定，SSI模型则演变为一系列的近似概率计算方法，如一次二阶矩法、二次二阶矩法等。在实际工程中，这些近似方法往往不仅需要对功能函数进行泰勒展开，还要完成非正态随机变量到正态变量的映射（如JC法）［3］，其实质是近似计算强度大于应力的概率。

需要指出的是，在传统SSI及其扩展模型中，通常假设应力与强度具有相同的量纲。文献［4］通过对传统SSI模型本质的深层次扩展，指出SSI模型实质上是随机加权模型，提出异量纲干涉模型的概念。通过异量纲干涉方法，传统的静态零部件可靠性模型可直接用于机械零部件的疲劳可靠度，从而使传统的SSI模型中嵌入了时间变量，也为机械系统时变可靠性建模提供了理论基础。此外，SSI模型主要用于机械零部件的可靠度计算，而机械系统的可靠度则由系统的结构函数和零部件可靠度获得。这种系统可靠度计算方法虽然物理意义明确且形式简单，但是，机械系统在传递载荷与运动的过程中，各零部件间由于具有共同的随机因素可能具有明显的失效相关性。事实上，失效相关广泛存在于机械系统中。文献［5］丰富了传统SSI模型的内涵，提出SSI模型直接用于系统可靠度计算的思路。研究中避免上述由下至上建模过程中关于零件失效独立的假设，基于次序统计量理论，通过系统级分析构建了考虑失效相关的系统可靠性模型。该模型不同于传统基于经验参数的可靠性模型，物理意义明确，揭示了机械系统中失效相关的发生机理与失效相关参数控制方法，并指出传统基于SSI模型的系统建模中存在的失效相关信息遗失现象，拓展了传统SSI模型的适用范围。静态机械系统可靠性定量评价方法研究已较为完善（如图1所示），该方法是目前机械系统静态可靠度分析的重要理论基础。

2　以失效率为输入变量的时变机械系统定量可靠性模型

尽管以SSI模型为基础的静态可靠性模型已取得了较大进展，但是，疲劳、磨损、腐蚀等失效模式大量存在于机械零部件中。机械零部件的强度往往由于疲劳裂纹的扩展以及材料的磨损等原因而不断退化。同时，载荷的随机特性在不同时刻也可能存在着较大的差异。机械系统可靠性往往具有明显的时变特征。因此，如何在机械系统定量可靠性分析模型中考虑时间因素具有重要的现实意义，同时也是目前可靠性研究的热点和难点问题。

可靠性的时变特性可通过失效率指标间接描述。而电子元器件具有失效率为常数、便于标准化、制造成本低、易于大样本试验统计等特征，因此以失效率为建模基本输入参数的时变可靠性模型被大量应用于电子系统可靠性分析［6-7］。机械可靠性分析大多沿用了电子领域可靠性评价方法。因此，上述时变可靠性分析方法也被广泛应用于机械系统的时变可靠性定量分析。该方法的主要原理是首先按照系统工作原理划分系统状态，再通过失效率假设和马尔可夫过程理论构建系统状态微分方程并求解系统可靠度。

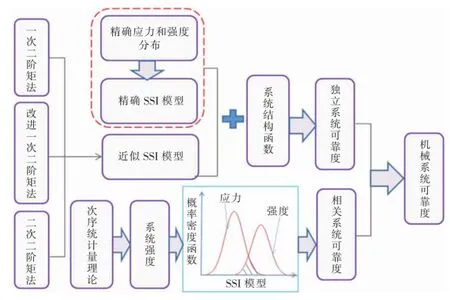
图1　机械系统静态可靠度定量计算方法及原理图示Fig.1　Quantitative calculation method and principle of static reliability of mechanical system

尽管基于失效率和马尔可夫过程原理的时变可靠性理论研究取得了较大的进步，但是，由于机械系统与电子系统在工作模式和失效模式上的本质区别，这种模型在实际应用中面临着以下的一些问题:

1）恒定失效率的假设往往不适用于机械零部件。此外，机械零部件由于功能任务的不同，在几何形状和材料等方面存在较大差异，相对于电子元器件不便于标准化。同时，失效率是工作载荷与零部件材料特性共同作用的结果，任何因素的变化均可能引起失效率时变函数的较大变化。所以，通过大样本实验获取各种机械零部件时变失效率的方法往往不可行。如何基于系统和零部件的失效机理构建能够考虑机械零部件设计、制造和使用过程中各种随机因素的通用时变失效率模型有待于进一步的研究。

2）在并联系统及表决系统中，如果考虑强度退化等因素的影响，机械零部件失效率通常是随时间变化的，并且零部件的时变失效率受到系统工作元件个数和强度退化的共同影响。此时，系统状态演变过程一般不能用马尔可夫过程来描述。系统时变可靠度微分方程形式复杂，解析解求解困难。即使使用数值方法对微分方程求解，也可能存在非线性方程对初始值和求解步长敏感等因素所造成的求解稳定性问题。因此，如何建立能够合理表征零部件性能退化的随机微分方程是有待深入研究的重要问题。

3　基于应力强度干涉原理的时变机械系统可靠性模型

除了以失效率为参数的系统可靠性模型，基于应力强度动态干涉的系统时变可靠性模型也是机械系统时变可靠性分析的重要基础。该方法是静态应力强度干涉理论的直接扩展。在模型中首先假设零件应力历程与强度退化历程为两个特定类型的随机过程（如图2所示）。相应的，各个时刻载荷与强度的分布也由随机过程的类型所确定［8-9］。此时的SSI模型成为某一时刻可靠度的计算模型（图2）。在此基础上，由系统失效准则可进一步建立系统时变可靠性模型。文献［10］提出了机械系统时变可靠性分析的理论框架。所提出方法从载荷和材料特性两个角度从不同层次详尽解释了时变干涉模型随机因素的来源。通过强度分布及其退化规律、载荷的宏微观统计分布、载荷作用次数分布各因素的分析，揭示了载荷历程样本不确定性效应、单载荷样本不确定性效应、载荷发生次数不确定性效应和零部件性能退化行为统计特性对机械系统时变可靠性的影响。

图2　应力强度动态干涉示意图Fig.2　Schematic diagram of dynamic interference between stressand strength

这种时变可靠性分析方法依赖于应力和强度退化历程的精确描述和统计，其核心问题是2个历程动态干涉的数学表达。当各时刻下应力与强度分布由多随机变量确定时，通常利用时变功能函数来处理动态干涉问题。尽管回归模型等方法的提出为这种模型的迅速发展起到了重要的作用［11］。但是，有关强度与应力历程两方面的以下问题却有待于进一步的研究:

1）直接采用各个时刻的剩余强度分布计算零部件可靠度时可能引起较大误差。例如，图3所示的仿真流程中，图3a用于模拟实际工作流程，并获得各个时刻剩余强度分布由失效数据计算可靠度，图3b基于图3a中获得的各时刻剩余强度分布求解可靠度。这两种仿真方法通常会得到不同的可靠度结果。这是由于随机载荷作用下的强度退化历程中相邻载荷作用时刻的剩余强度间具有明显的统计相关性。基于各时刻剩余强度分布假设的计算方法则忽略了这种相关性。此外，现有模型所假定的强度退化随机过程模型中统计参数的物理意义往往缺乏明确的解释。因此，如何以更易于实验测试的材料参数作为输入变量并考虑强度退化机理对随机载荷历程下的强度退化历程进行数学表达有待于进一步的研究。

图3　可靠性仿真框图Fig.3　Flow chart of reliability simulation

2）系统内零部件的应力随机过程由随机载荷历程计算获得。在由磨损、裂纹等原因引起的强度退化过程中，零部件的刚度、阻尼特性以及零部件间的传递载荷均表现出明显的时变特征。此时的机械系统为非自治系统，应力响应一般为非稳态随机历程，并且其频率和幅值与工作载荷之间不是线性关系。目前，线性系统平稳载荷以及非平稳载荷下的响应分析取得了较大进展［12-13］，统计线性化法等非线性系统的线性化等效方法也为非线性系统的随机响应分析提供了理论基础［14］。同时，线性和非线性随机有限元方法以及响应面法等近似方法也在复杂非线性系统的响应分析中发挥了重要的作用。但是，非稳态载荷下强非线性系统的解析随机响应求解问题和随机场离散化所引起的高维度随机场下系统响应自相关函数求解问题仍然有待于进一步的研究。此外，如何在时变非线性系统随机应力响应求解中考虑零部件的强度退化机理也是目前处理机械系统动态干涉时存在的主要问题。

3）机械每个零部件应力随机历程与强度随机退化历程之间、系统内各零部件强度退化历程之间由于工作载荷以及机械零部件几何和材料特性的共同作用而具有相关性。事实上，这种相关性广泛存在于机械系统，对该相关性的准确揭示和数学表达对机械系统时变可靠性分析具有重要意义。

4　结论

机械系统定量可靠性模型是机械产品可靠性精确评价、优化设计和质量管理的重要理论基础。本研究从定量静态模型和时变模型2个角度阐述了现有重要定量模型的建模基本原理、研究现状以及存在的问题。目前，静态定量可靠性模型的研究相对成熟，但该模型无法考虑时间因素对可靠性的影响。当系统中零部件存在性能退化时，定量时变可靠性模型成为主要的理论分析基础。机械系统时变可靠性分析理论是机械可靠性研究的重要问题。由于机械失效率在统计测试方便的困难，基于应力强度动态干涉原理的系统可靠性模型更适于机械产品可靠性的定量分析。但是，在建模过程中，应充分考虑应力与强度历程的统计和数学表达以及动态干涉过程中的强度退化历程相关性问题。

［1］Moss T R，Andrews J D.Reliability assessment of mechanical systems［J］.Proceedings of the Institution of Mechanical Engineers，Part E:Journal of Process Mechanical Engineering，1996，210（3）:205-216.

［2］Freudenthal A M.Safety of structures［J］.Transaction on ASCE，1947，112:125-180.

［3］Rackwitz R，Fiessler B.Structural reliability under combined random load sequences［J］.Computers and Structures，1978，9 （5）:489-494.

［4］谢里阳，王正.随机恒幅循环载荷疲劳可靠度异量纲干涉模型［J］.机械工程学报，2008，44（1）:1-6.

［5］谢里阳，李翠玲.相关系统失效概率的次序统计量模型及共因失效原因分析［J］.机械强度，2005，27（1）:66-71.

［6］Vaurio J K.An implicit method for incorporating common cause failures in system analysis［J］.IEEE Transaction on Reliability，1998，47（2）:173-180.

［7］Chae K C，Clark G M.System reliability in the presence of common-cause failures［J］.IEEE Transaction on Reliability，1986，35（1）:32-35.

［8］Bilikam J E.Some stochastic stress-strength processes［J］.IEEE transactions on reliability，1985，3:269-274.

［9］ Aminzadeh M S.Estimation of P（Z＜Y）for correlated stochastic time series models［J］.Applied Mathematics and Computation，1999，104（2）:179-189.

［10］谢里阳.扩展式可靠性建模方法与四元统计模型［J］.中国机械工程，2009，20（24）:2969-2973.

［11］Zuo M J，Jiang R，Yam R.Approaches for reliability modeling of continuous-state devices［J］.IEEE Transactions on Reliability，1999，48（1）:9-18.

［12］ LiangJ，ChaudhuriSR，ShinozukaM.Simulationof nonstationary stochastic processes by spectral representation ［J］.Journal of Engineering Mechanics，2007，133（6）:616 -627.

［13］Mao C，Jiang Y，Wang D，et al.Modeling and simulation of non-stationaryvehiclevibrationsignalsbasedonHilbert spectrum［J］.Mechanical Systems and Signal Processing，2015，50-51:56-69.

［14］Caughey T K.Equivalent linearization techniques［J］.The Journal of the Acoustical Society of America，1963，35（11）: 1706-1711.

Review on Quantitative Evaluation Methods of Mechanical System Reliability

GAO Peng1，XIE Li-yang2
（1.Liaoning Shihua University，College of Mechanical Engineering，Liaoning Fushun 113001，China；
2.Northeastern University，Ministry of Education Key Laboratory of Aero Power Equipment Vibration and Control，Shenyang 110819，China）

With mechanical product structures and working environment becoming more and more complex，correct evaluation on mechanical system reliability has important practical significance for the product quality evaluation and the whole life cycle management.In this paper，modeling principles as well as research status and problems of the existing quantitative reliability models of mechanical systems are briefly introduced.It is pointed out thatthe research on static system reliability models is relatively mature and the traditional stress strength interference model can be extended to evaluate reliability of mostmechanical components and mechanical systems.However，when the strength of components degenerates，time has to be taken into consideration in reliability analysis of mechanical systems and traditional static reliability models are incapable of analyzing timedependent reliability of mechanical systems.Therefore，key problems in establishing time-dependent reliability of mechanical systems are described in this paper.

reliability；mechanical system；failure rate；interference model

TB114

A

10.3969/j.issn.1673-6214.2016.01.008

1673-6214（2016）01-0037-05

2015年9月5日

2015年12月28日

国家自然科学基金（51505207）；国家自然科学基金（51175072）；辽宁省教育厅科学研究一般项目（L2015298）；辽宁省自然科学基金（2015020152）

高鹏（1982年-），男，博士，副教授，主要从事机械系统可靠性与机械动力学等方面的研究。