一种参数自适应的Harris角点检测算法

赵　萌，温佩芝，邓　星，成　龙

(1.桂林电子科技大学 电子工程与自动化学院,广西 桂林　541004；2.桂林电子科技大学 计算机与信息安全学院,广西 桂林　541004)



一种参数自适应的Harris角点检测算法

赵萌1，温佩芝2，邓星2，成龙1

(1.桂林电子科技大学 电子工程与自动化学院,广西 桂林541004；2.桂林电子科技大学 计算机与信息安全学院,广西 桂林541004)

针对用固定高斯函数参数σ值及人为设定阈值时角点检测不准确的问题，提出一种σ自适应的Harris算法。在选定区域内设置多个σ值提取Harris预选角点，对非极大值抑制时，采用自适应阈值获得预选角点；对不同σ值生成的预选角点响应函数R采用约束准则筛选出最大值，从而提取出有效的角点，去除伪角点。实验结果表明，本算法具有较好的图像角点检测性能，能够获得更多有效角点和更少伪角点。

Harris角点检测；高斯函数参数σ；自适应；阈值

角点未有精确的数学定义，通常指图像中梯度值和梯度变化率都非常大的像素点以及图像边缘曲线曲率极大值的像素点，它能反映出图像的局部特征，在降低信息数据量的同时有效地保留了图像的重要特征[1]。因此，角点检测在目标辨识、目标跟踪、相机标定、三维测量、运动估计、图像配准与匹配等计算机视觉处理中起着至关重要的作用。目前，角点检测方法主要有2大类：

1)基于图像边缘轮廓特征的方法。此方法需要经过图像预分割、轮廓链码提取和角点检测，如基于边界曲率的角点检测[2]，基于边界小波变换的角点检测[3]以及基于边界链码的角点检测[4]。

2)基于图像灰度信息的方法。此方法主要通过计算曲率及梯度进行角点检测，通过计算边缘的曲率来判断角点的存在性。典型代表有Harris算法[5]、Susan算法[6]、Moravec算法[7]等。

Schmid等[8]指出，在基于图像灰度的方法中Harris算法是角点检测效果最好的，其计算简单，稳定性强，具有对光照、相机姿态变化、旋转和仿射均不变的特性，因此得到了广泛的应用。众多学者基于经典的Harris角点检测算法进行了改进，如赵万金等[9]应用图像分块与邻近点剔除相结合的思想来避免阈值的设置，保证了角点分布均匀，且具有紧支性与良好的逼近能力。王玉珠等[10]依据B样条函数收敛于高斯函数，且具有紧支性与良好的逼近能力，用B样条函数替换了经典Harris算法中的高斯函数。汪成亮等[11]用分数阶微分代替原算法中的整数阶微分对图像做微分运算，并引入分形维数，自适应地选择分数阶微分中所需的参数。He等[12]根据统计特性对Harris算法进行了改进。龙忠杰等[13]应用邻域像素取差法改进Harris算法，并加入Susan特性去除伪角点，使改进算法更加有效。李鹏程等[14]通过圆形区域进行了非极大值抑制，降低了角点检测时间。毛雁明等[15]针对非极大值抑制时不易设置阈值问题，提出相对大和相对小的双阈值法。房超等[16]利用双掩膜结合K均值聚类方法进行非极大值抑制，回避了阈值的设置。以上改进算法虽取得了一定成效，但均在固定高斯函数参数σ值下进行，然而Harris算法对噪声很敏感，虽然采用了高斯函数对噪声进行抑制，但不同的σ值对检测结果有很大的影响[17]。当σ值较小时，高斯函数对噪声的抑制较弱，角点检测结果的稳定性差；而σ值较大时，抗噪性强，对角点过于平滑，降低了角点响应函数R的值或使邻近角点的响应交叠，从而影响角点提取的精度。实际使用时，阈值需人为多次设定才可得到相对理想的结果。

鉴于此，结合多个σ值和自适应阈值对Harris算法进行改进。利用Harris算法在选定区域内设置多个σ值进行角点检测，对非极大值抑制时采用角点响应函数最大值的倍数作为阈值[18]，自适应地设置阈值来提取预选角点，并采用文献[19]的方法修改角点响应函数，避免了人为设置阈值与角点响应函数中系数k的随机性和反复性。采用约束准则对不同σ值产生的预选角点响应函数R筛选出峰值最大的点作为角点，从而提取出有效角点，去除伪角点。

1　Harris角点检测的原理

Harris角点检测算法于1988年由Harris等[5]提出，是在Moravec算法的基础上改进的一种基于信号的点特征提取算法。Harris角点检测算法采用微分运算与自相关矩阵进行角点检测。微分算子能反映像素点沿任何方向的灰度变化，可以很好地区分边缘与角点。与自相关函数有关联的矩阵Μ的特征值是自相关函数的一阶曲率，若某像素点在x、y方向的曲率都很高，则该像素点被认为是角点。

假设像素点(x,y)的灰度为I(x,y)，以像素点(x,y)为中心的窗口移动微小的位移(u,v)后的灰度变化为：

(1)

其中，w(x,y)=exp[-(x2+y2)/2σ2]为二维高斯平滑函数，对自相关函数起低通平滑的作用，以提高算法抵抗噪声的能力。一阶导数X、Y可用一阶微分近似：

(2)

其中⊗表示卷积。对于微小的位移可忽略高次阶O(u2,v2)，因此灰度强度可近似为：

E(u,v)=Au2+2Cuv+Bv2。

(3)

其中：A=X2⊗w；B=Y2⊗w；C=(XY)⊗w。

灰度强度的二次型为：

(4)

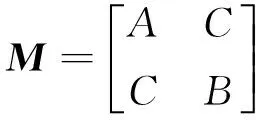
为了避免对矩阵直接求解特征值，用矩阵的行列式和迹表示角点响应函数：

(5)

其中：det(M)=λ1λ2=AB-C2；tr(M)=λ1+λ2=A+B；k为常量，通常取值0.04～0.06。每个像素点在其自身为中心的邻域内，若该像素点响应函数在其邻域内为最大值且超过设定的某个阈值，则该像素点被认为是角点。

尽管经典Harris角点检测算法计算简单，且具有对光照、相机姿态变化、旋转和仿射不变的特性。但仍存在以下缺陷[19]：

1)σ参数对Harris算法影响较大。采用固定σ值检测角点，可使Harris算法提取伪角点，漏掉部分有效的角点，定位精度差，同时该算法对噪声相对较敏感。

2)Harris算法提取角点时，尽管对响应函数进行了非极大值抑制，然而阈值的设定决定了角点提取的结果，阈值偏大时有效角点会丢失,阈值偏小时伪角点会出现。

3)虽然Harris算法选用的高斯平滑函数窗口可调，但实际使用中很难掌握高斯窗口的尺寸。若高斯平滑函数窗口选取偏大，则由于卷积的圆角效应导致角点位置的偏移；若高斯平滑函数窗口选取偏小，则由于噪声的影响呈现较多的伪角点。

4)对图像做平滑滤波时，若采用光滑的高斯函数，则因过平滑引起丢失有效角点信息，且无法对此角点丢失给予弥补。

2　改进的参数自适应Harris角点检测算法

由于Harris角点检测算法提取角点时采用了固定的σ值，当σ值较小时，高斯函数的抗噪性弱，会影响角点提取的稳定性，有效角点周围会出现聚簇现象，错误检测的比例增加，但定位准确；当σ值较大时，高斯函数的抗噪性强，对角点过于平滑，使R值降低，角点的定位产生偏移，丢失有效角点。因此，在固定σ值的角点提取过程中，存在有效角点信息的丢失和伪角点被提取的问题。平滑的角点模型由于光学低通的作用，使角点在图像过渡区并非阶梯状，而存在一定的宽度w，对于性能稳定的角点，存在理想的σ值。角点响应值R、过渡区宽度w、σ之间的关系如图1所示[17]。

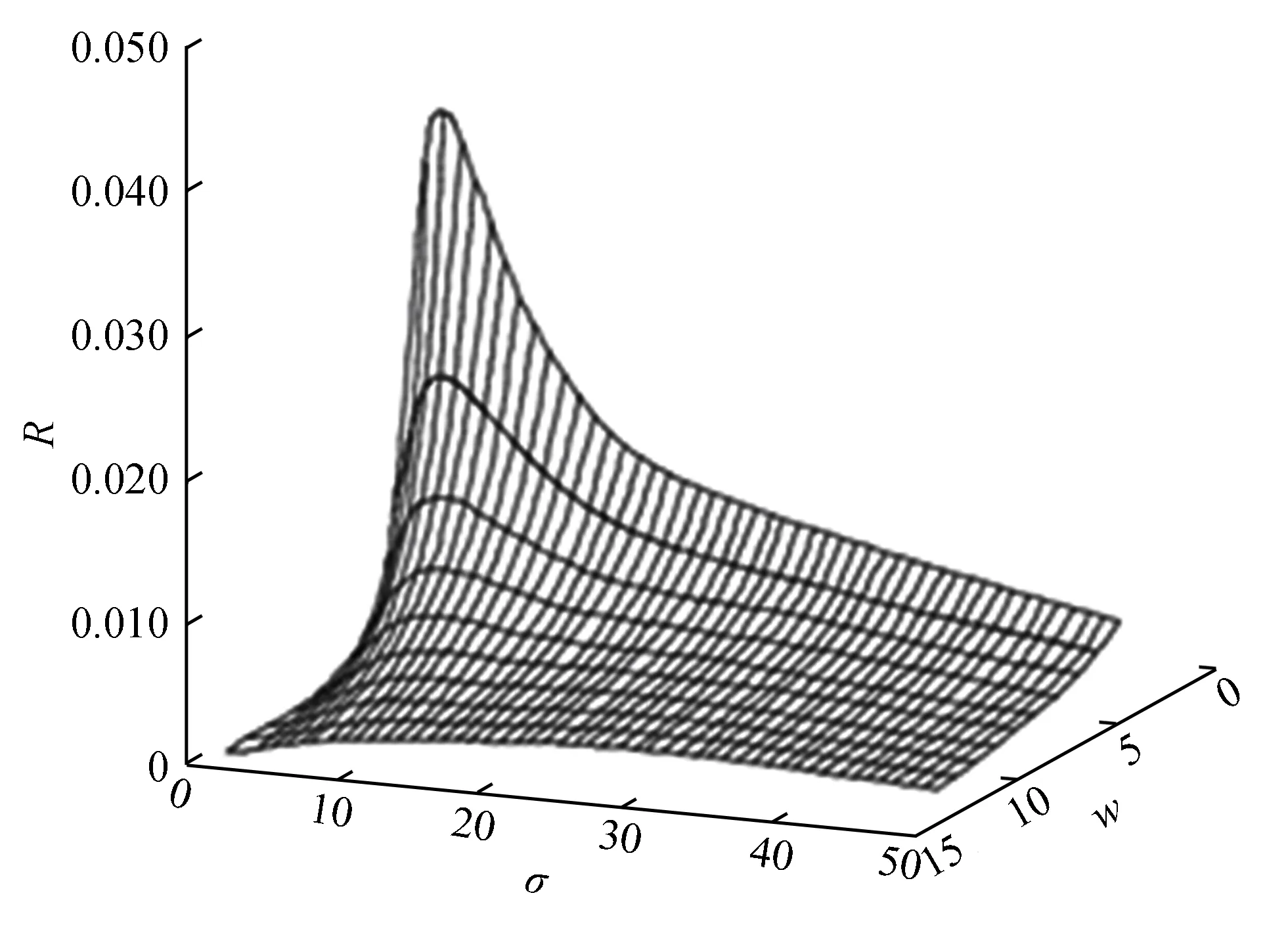
图1　R与w和σ之间的关系Fig.1　The relationship of R,σ,w

从图1可看出，对于不同角点的w，总存在一个与此相匹配的理想的σ。因此，提出一种σ自适应的Harris算法，在选定区域内设置不同的σ值来进行Harris预选角点的提取，然后采用约束准则对不同的σ值产生的预选角点响应R进行筛选，以角点响应函数峰值最大的一组为理想结果。改进算法步骤如下：

1)求取Μ。彩色二维图像变换为灰度二维图像，计算灰度二维图像上像素点(x,y)在水平方向与垂直方向上的梯度Ix、Iy及其乘积，获得3幅新图像与M的4个元素值，采用Prewitt算子提取边缘，计算Ix、Iy，则有

(6)

离散二维零均值高斯函数w(x,y)对获得的3幅新图像进行滤波,获得新Μ。

2)计算每个像素点(x,y)在原二维灰度图像上对应的响应函数R。经典的Harris角点检测算法中的响应函数R=det(M)-k(tr(M))2，由于需要多次调节系数k来获得理想的检测结果，降低了算法的效率。为此，采用文献[19]的方法对R进行修改：

(7)

其中ε为任意小的正数。修改后的响应函数无需对矩阵直接求解，且避免了人为设定系数k的随机性。在Harris算法中，局部区域内的极大值对应的像素点若被认为是角点，则响应函数值应大于阈值。经典Harris算法需要人为设置阈值，对角点响应函数进行非极大值抑制，获得局部极大值后，由阈值的设置决定角点提取的结果。考虑到对不同的图像需要设定不同的阈值，本算法将阈值设定为角点响应函数最大值Rmax的p倍[18]，即T=p×Rmax，其中p值选定为0.05～0.075，以避免阈值设定的盲目性、反复性。

3)在选定区域内设置多个σ值，对图像按Harris算法进行预选角点提取，对每个σ值产生的预选角点响应值R采用约束准则进行筛选。若第一个σ值下的角点在第二个σ值下的相同位置及邻近区域出现，则以角点响应函数峰值最大的一组为理想结果，否则删除此角点，依次比较，去除伪角点，保留有效角点，最终获得不同σ值下的角点。

3　实验与分析

为对本算法的检测性能进行验证，选择角点比较明显的积木、几何图形以及真实古建筑窗户3组图像，对经典Harris算法、阈值自适应Harris算法和本算法的实验结果进行编程和对比分析。实验环境为Inter(R)Core(TM)2处理器、2GB内存、64位Window8.1操作系统、MatlabR2013b。

积木角点检测结果如图2所示，几何图形角点检测结果如图3所示。对图2、图3角点检测结果的数据统计分别如表1、表2所示。表1、表2中的正确数表示检测出的角点数，漏检数表示未被检测出的角点数，误检数表示检测出的非角点数，准确率为检测到的角点数与图像中的总角点数之比。

图2　积木角点检测Fig.2　Corner detection of building block

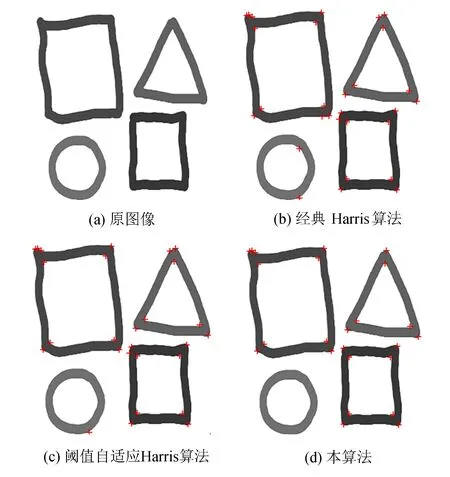
图3　几何图形角点检测Fig.3　Corner detection of geometric figures

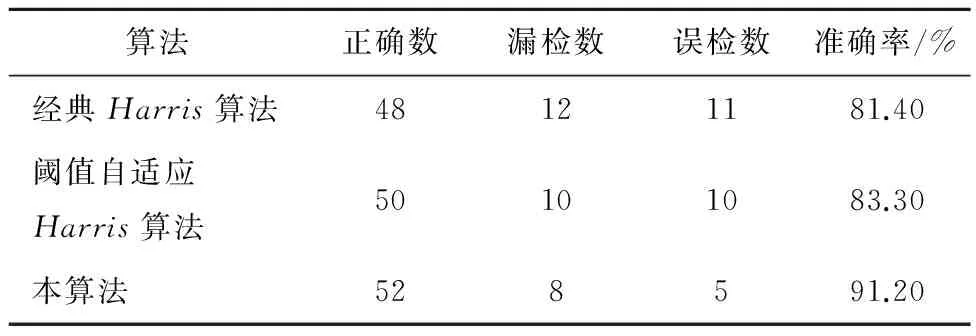
算法正确数漏检数误检数准确率/%经典Harris算法48121181.40阈值自适应Harris算法50101083.30本算法528591.20

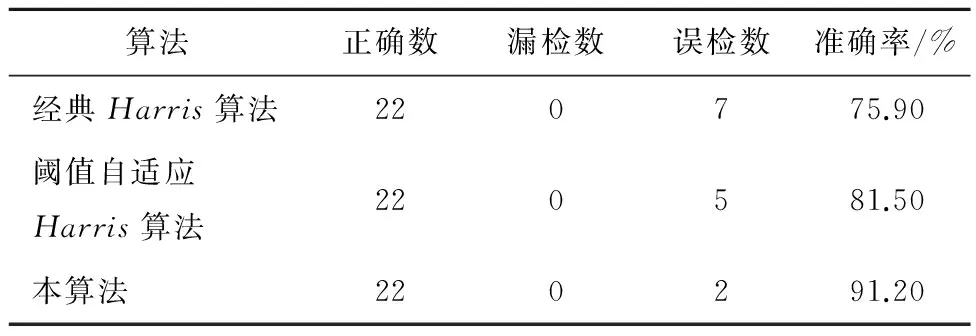
表2　几何图形角点检测结果

从图2、图3和表1、表2可看出，本算法具有较好的图像角点检测性能，能够获得更多的有效角点和更少的伪角点。

古建筑局部窗户角点检测结果如图4所示。从图4可看出，本算法删除了大量的伪角点，保留了更多的有效信息点，角点分布比较均匀，而经典Harris算法中角点聚簇现象严重，自适应阈值Harris算法仍有较多伪角点，因此本算法具有较好的检测效果。

经典Harris算法采用单一的σ值、固定阈值提取角点，针对一幅图像具有较好的提取结果，但其σ值、阈值不一定适应其他图像，在实际应用中，如发现效果差，需要重新设定参数，较为繁琐且效率低。自适应阈值Harris算法的阈值虽然自适应于所检测图像，但σ仍为固定单一值。本算法采用了自适应的思想，阈值设定为最大角点响应函数值的倍数，此倍数由经验值得到，应用多组σ值，以角点响应函数峰值最大的一组为理想结果，角点在不同σ值下提取，得到了较好的提取结果，减少了对实验的调整次数，提高了效率。

4　结束语

在继承经典Harris算法计算简单、稳定性强等优点的基础上，针对其采用固定σ值及人为设定阈值检测角点存在的不足，结合多组σ值和自适应阈值对Harris算法进行了改进。用多组σ值进行Harris预选角点提取，采用约束准则对不同σ值产生的预选角点响应函数R进行筛选，提取不同σ值下的角点，利用参数的自适应实现了不同σ值下角点的有效提取。在预选角点提取过程中修改角点响应函数R，并对非极大值抑制时采用自适应阈值获得预选角点，避免了人为设置阈值的随机性和反复性。与经典Harris算法及自适应阈值Harris算法对比的实验结果表明，本算法具有较好的图像角点检测性能，能够获得更多有效角点，减少伪角点，更具实用性。但本算法存在运算时间略长的问题，这是今后进一步优化的方向。

[1]赵文彬，张艳宁.角点检测技术综述[J].计算机应用研究，2006(10):17-19.

[2]MOKHTARIANF,SUOMELAR.Robustimagecornerdetectionthroughcurvaturescalespace[J].IEEETransactionsonPatternAnalysisandMachineIntelligence,1988,6(1):121-128.

[3]HUAJP,LIAOQM.Multiscalecornerdetectionbyusingwavelettransform[J].IEEETransactionsonImageProcessing,1995,4(1):100-104.

[4]FREEMANH,DAVISLS.Acorner-findingalgorithmforchain-codedcurves[J].IEEETransactionsonComputer,1977,26(3):297-303.

[5]HARRISCG,STEPHESMJ.Acombinedcornerandedgedetector[C]//ProceedingsofFourthAlveyVisionConference,1988:147-151.

[6]SMITHSM,BRADYJM.SUSAN-Anewapproachtolowlevelimageprocessing[J].InternationalJournalofComputerVision,1997,23(1):45-78.

[7]MORAVECHP.Towardsautomaticvisualobstacleavoidance[C]//Proceedingsofthe5thInternationalJointConferenceonArtificialIntelligence,1977:584-590.

[8]SCHMIDC,MOHRR,BAUCKHAGEC.Evaluationofinterestingpointdetectors[J].InternationalJournalofComputerVision,2000,37(2):151-172.

[9]赵万金，龚声蓉，刘纯平，等.一种自适应的Harris角点检测算法[J].计算机工程，2008,34(10):212-217.

[10]王玉珠，杨丹，张小洪.基于B样条的改进型Harris角点检测算法[J].计算机应用研究，2007(2):192-194.

[11]汪成亮，乔鹤松，程娟娟.基于自适应分数阶微分的Harris角点检测算法[J].计算机应用，2011,31(10):2702-2704.

[12]HEBaigen,MINGZhu,WEIYajuan.AmatchingalgorithmonstatisticalpropertiesofHarriscorner[C]//ProceedingsoftheIEEEInternationalConferenceonInformationandAutomation,2011:226-229.

[13]龙中杰，王吉芳，左云波.一种改进的Harris与Susan相结合的角点检测方法[J].计算机应用与软件，2013,30(12):133-136.

[14]李鹏程，曾毓敏，张梦.一种改进的Harris角点检测算法[J].南京师大学报(自然科学版)，2014,37(2):49-54.

[15]毛雁明，兰美辉，王运琼，等.一种改进的基于Harris的角点检测方法[J].计算机技术与发展，2009,19(5):130-133.

[16]房超，王小鹏，牛云鹏，等.基于改进Harris算法的角点检测[J].计算机与数字工程，2011,39(5):142-144.

[17]张益昕.基于计算机视觉的大尺度三维几何尺寸测量方法及应用[D].南京：南京大学，2011:49-50.

[18]沈士吉，张小龙，衡伟.一种自适应阈值的预筛选Harris角点检测方法[J].数据采集与处理，2011,26(2):207-213.

[19]张小洪，李博，杨丹.一种新的Harris多尺度角点检测[J].电子与信息学报，2007,29(7):1735-1738.

编辑：张所滨

A parameter adaptive Harris corner detection algorithm

ZHAO Meng1, WEN Peizhi2, DENG Xing2, CHENG Long1

(1.School of Electronic Engineering and Automation, Guilin University of Electronic Technology, Guilin 541004, China;2.School of Computer and Information Security, Guilin University of Electronic Technology, Guilin 541004, China)

Corner detection is not accurate with a fixed Gaussian function parameter σ and artificially set value, so a σ parameter adaptive Harris algorithm is put forward. Gaussian function parameter σ is set in the selected region to extract preselected Harris corner. and in the process of non maximal suppression, the adaptive threshold is used to obtain the preselected angular point. The constraint criterion is adopted to choice the maximum from each σ parameter generation of the preselected angular point response functionR, the effective corners are extracted and the false corners are removed. The experimental results show that this algorithm has better image corner detection performance, and can get more effective corners and less false corners.

Harris corner detection; Gaussian function parameter σ; adaptive; threshold

2016-01-13

广西科学研究与技术开发计划(桂科攻1598010-7，桂科攻14124005-2-9)；桂林电子科技大学研究生教育创新计划(GDYCSZ201418)

温佩芝(1963-)，女，广西灵山人，教授，博士，研究方向为数字图像处理、目标检测与模式识别。E-mail:48566433@qq.com

TP394.41

A

1673-808X(2016)03-0215-05

引文格式： 赵萌，温佩芝，邓星，等.一种参数自适应的Harris角点检测算法[J].桂林电子科技大学学报，2016,36(3):215-219.