裂纹条件下轴类锻件锻造中温度场分析模型

付献斌　张玉存　董志明　张雷强

1.河北环境工程学院，秦皇岛，066102　　2.燕山大学,秦皇岛,066004



裂纹条件下轴类锻件锻造中温度场分析模型

付献斌1张玉存2董志明2张雷强2

1.河北环境工程学院，秦皇岛，0661022.燕山大学,秦皇岛,066004

基于非稳态热传导理论建立了对称与非对称裂纹条件下轴类锻件的二维温度场分析模型。该模型结合复合介质理论，首先运用集总参数法求解对称裂纹锻件的裂纹介质温度场，得出裂纹对应的温度场函数，然后将其作为对称裂纹条件下轴类锻件热传导方程的边界条件，通过求解热传导方程得到对称裂纹条件下轴类锻件的温度场分析模型；其次，通过引入修正系数得到非对称裂纹的温度场函数，将该温度场函数作为非对称裂纹条件下轴类锻件热传导方程的边界条件，求解热传导方程得到非对称裂纹条件下轴类锻件的温度场分析模型。实验验证了该模型的可行性。

轴类锻件；裂纹；复合介质；非稳态热传导理论；温度场

0　引言

轴类锻件作为大型成套设备的核心零部件[1]，其质量直接关乎国家能源安全和人民群众的生命财产安全。裂纹作为轴类锻件锻造过程中的常见缺陷，其存在会直接影响锻件质量，给安全生产带来隐患。在轴类锻件锻造过程中，实时掌握锻件温度场,特别是其外表面温度场的变化情况，对保证锻造工艺准确实施，提高锻件质量尤为重要[2]。

近年来，国内外许多学者对包括轴类锻件在内的锻件温度场进行了深入的研究。Lee[3]采用有限元软件、Fourier方程及拉氏变换等方法对三维物体进行了温度场数值分析。Lu等[4]通过建立多维复合圆柱瞬态温度场，得到了复合圆柱瞬态温度场的变化规律。关明等[5]通过实验模拟实际生产中的锻件建立了Mn18Cr18N护环钢锻造中的温度场，对在一定保温措施下锻件的温度场变化情况进行了描述。张艳芹等[6]建立了模拟静压轴承的温度场模型，得出了轴承周期端面较准确的不对称温度分布规律。张玉存等[7]在热传导理论的基础上，建立了大型筒类锻件的温度场检测模型。综上所述，目前大部分学者都是对正常锻件温度场进行研究，对含缺陷轴类锻件温度场的研究较少，故本文对裂纹条件下轴类锻件锻造中的温度场进行分析。

本文在非稳态热传导理论的基础之上，结合复合介质理论建立了裂纹条件下轴类锻件锻造中的温度场分析模型。通过求解模型得到锻件外表面温度场变化规律，进而对锻造中的锻件内部状态进行判断。

1　裂纹条件下轴类锻件温度场分析模型

假设轴类锻件中的裂纹存在对称和非对称两种形式，如图1、图2所示。其中，r1、r2分别为裂纹和锻件的半径。

图1　含对称裂纹的轴类锻件

图2　含非对称裂纹的轴类锻件

1.1对称裂纹条件下轴类锻件温度场分析模型

对称裂纹位于轴类锻件中心位置，由于裂纹尺寸相对锻件小得多，故采用集总参数法进行分析。裂纹与裂纹外围锻件的能量控制方程为

(1)

初始条件和边界条件为

(2)

式中，T1、T2分别为轴类锻件裂纹部分和裂纹外围锻件的温度分布函数；h1、h2分别为裂纹和外围锻件间的传热系数、锻件与外界环境间的对流传热系数；T0为初始时刻轴类锻件与裂纹的温度；T∞为外界环境温度；ρ1、c1、A1、V1和ρ2、c2、A2、V2分别为轴类锻件裂纹部分与裂纹外围部分的密度、质量热容、表面积和体积。

求解控制方程得到包含T1的微分方程的通解为

T1=T∞+Mem1t+Nem2t

(3)

m1={-(P1+P2+P3)+

m2={-(P1+P2+P3)-

将初始条件代入式(3)，求得裂纹温度：

(4)

一般认为含对称裂纹锻件为复合介质，并将裂纹温度T1作为裂纹外围介质的边界条件，为分析方便,忽略轴类锻件端部传热效应，则锻件的传热问题便转化为第三类边界条件下的二维非稳态传热问题，热传导方程为

(5)

式中，Tw为含对称裂纹轴类锻件裂纹外围锻件的温度场，Tw=p(r,z,t)；α1为轴类锻件的热扩散率；k为裂纹外围锻件的热导率；f(r)为初始时刻锻件给定温度分布；h3为锻件外侧与环境的对流传热系数；p1(t)为r=r1、t>0时对称裂纹条件下轴类锻件温度场的边界条件；p2(t)为r=r2、t>0时的边界条件；t为所经过的时间。

对Tw(r,z,t)中变量r进行正积分、逆积分变换，得到如下形式：

(6)

(7)

H0(γm,r)=cos(γmr)

式中，γm为γmtan(γmr1)=h3的根；r′为对r进行逆变换后的变量。

用式(7)对热传导方程进行积分变换，有

(8)

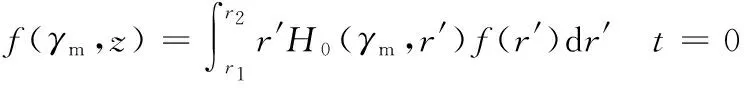
(9)

(10)

(11)

M(εj,z)=cos(εjz)

式中，εj为εjtan(εjr2)=h3的根。

利用积分变换式(11)对式(8)进行变换得

(12)

对式(12)进行积分逆变换，最终求得

(13)

式(13)即为对称裂纹条件下轴类锻件的温度场分析模型，通过代入相应位置信息即可求得锻件表面指定位置处的温度值。

1.2非对称裂纹条件下轴类锻件温度场分析模型

当裂纹位于锻件近表面位置处时，该锻件被认为是非对称裂纹锻件。此时利用集总参数法求得的裂纹温度与对称裂纹存在差异，实际上在t>0时，非对称裂纹的温度比对称裂纹温度要低。故我们在非对称裂纹温度中引入修正系数b′，于是有：

(14)

修正系数反映了对应裂纹与锻件中心轴线偏离距离之间的关系，这符合热传递过程中的实际情况。同样,视非对称裂纹锻件为复合介质，依然忽略锻件端部传热，因此，非对称裂纹条件下轴类锻件的二维非稳态热传导方程为

(15)

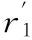
采用式(7)对式(15)进行变换可得

(16)

(17)

求解式(16)，并经积分变换最终求得

(18)

式(18)即为最终求得的非对称裂纹条件下轴类锻件的温度场分析模型，同样通过代入相应位置信息即可求得锻件表面指定位置处的温度值。

2　实验验证

2.1仿真实验

利用有限元仿真软件Comsol Multiphysics建立具有对称和非对称内部裂纹的轴类锻件传热模型，得到锻件的温度场分布，锻件的参数如下：材料为45钢，其热导率为26.49 W/(m·K)，直径为0.13 m，长度为0.50 m，外壁对流传热系数为20 W/(m2·K)，裂纹半径为0.01 m，长度为0.10 m。含对称与非对称裂纹锻件表面轴向设定点的温度仿真分布如图3所示。

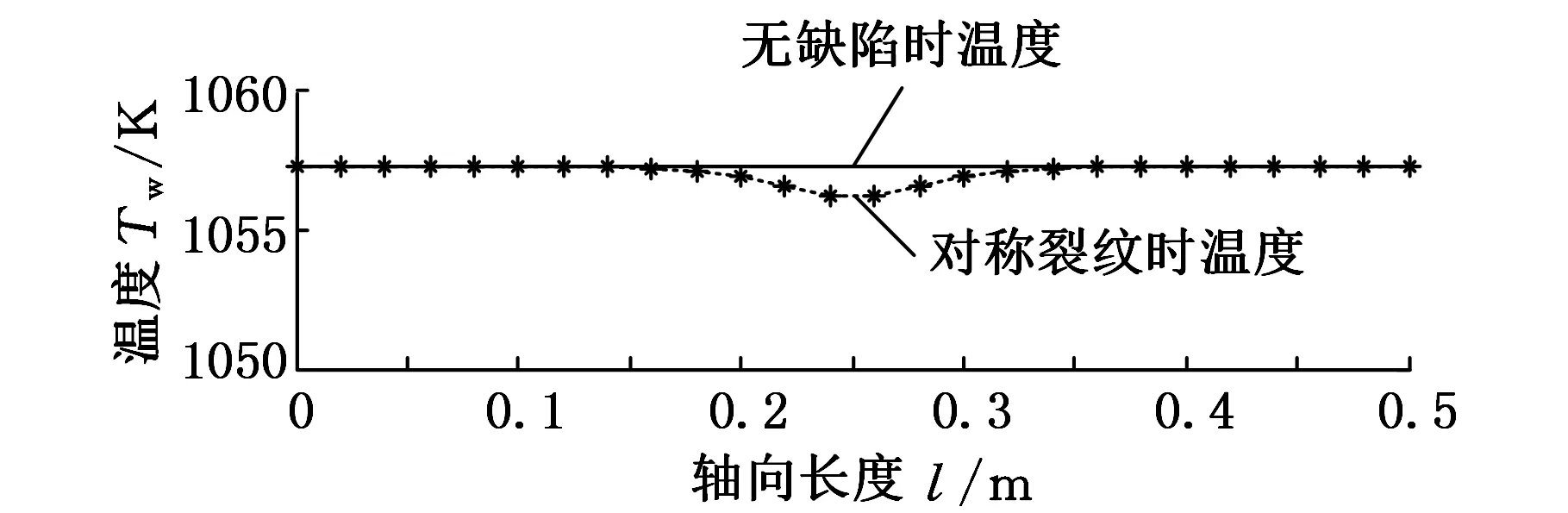
(a)含对称裂纹锻件表面轴向设定点的温度

(b)含非对称裂纹锻件表面轴向设定点的温度图3　含对称与非对称裂纹锻件表面轴向设定点的温度仿真分布

图3a采样得到的温度曲线变化较缓慢，图3b采样得到的温度曲线变化较为强烈。温度的显著降低，说明缺陷距离锻件外壁较近，且距离越近温度下降得越显著；温度变化越平缓，说明缺陷距离锻件轴向中心位置越近。

通过以上温度场分析模型仿真分析可知，该模型能够通过外表面的温度变化对锻件内部缺陷进行预判。

2.2实验

由于锻件锻造现场环境复杂，对流传热系数较大，考虑到实验的成本和安全性，选取实验对象为45钢圆柱锻件。实验参数为：锻件长0.50 m，直径0.13 m；裂纹长0.10 m，半径0.01 m。实验中首先应用超声波探测器对选取的45钢圆柱锻件进行检测，以确定锻件没有任何缺陷；然后，在锻件一个端面中心轴线(或非中心轴线)位置钻取一个指定大小与深度的柱形裂纹；最后，切削加工出直径与钻取柱形裂纹材料直径一致的柱形孔，且将长度小于柱形裂纹的细圆柱棒塞入锻件柱形裂纹中，便完成了锻件内置裂纹的设置。将设置好的45钢圆柱锻件放置加热炉加热至1000 ℃(保温半小时)，取出锻件放置室温空冷。

通过红外热成像仪检测锻件表面温度，并与热电偶温度传感器测量温度进行对比以保证实验数据的准确性。图4所示为实验中用红外热成像仪获得锻件表面设定点温度的实验设备。

图4　获得锻件表面设定点温度的实验设备

考虑锻件两端面实际传热的影响，提取锻件中心位置轴向两侧10个设定点的温度分布数据。含对称和非对称裂纹圆柱锻件表面轴向为l的圆周上、不同角度φ上的温度分布如表1和表2所示。

表1　含对称裂纹轴类锻件不同轴向长度圆周上的温度分布数据表　K

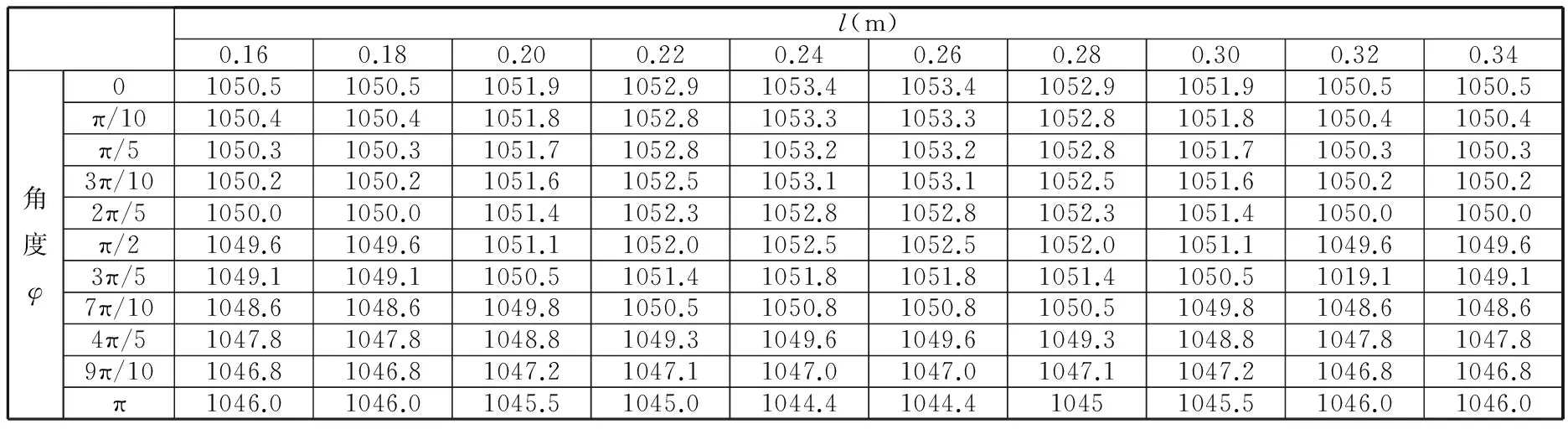
表2　含非对称裂纹轴类锻件不同轴向长度圆周上的温度分布数据表　K

从表1中可以看出，含对称裂纹锻件的表面温度变化比较平缓。为了更加明确地看出锻件外表面温度变化趋势，用曲面图对锻件外表面展开后的温度分布进行表示。图5为含对称裂纹轴类锻件不同轴向长度圆周上的温度分布曲面图。

图5　含对称裂纹轴类锻件不同轴向长度圆周上的温度分布曲面图

从图5中可以看出：锻件轴向长度0.22 m到0.28 m段局部外表面温度呈现缓慢下降趋势；从方位角角度看，锻件温度变化不明显，由此可知锻件中心轴线位置出现裂纹。这一结果符合缺陷处于锻件中心位置的实际情况，实验中采用热电偶测量的锻件外表面温度与采用红外热像仪测量的温度基本一致。

从表2中可以看出，含非对称裂纹锻件的表面出现了许多温度明显低于其他位置温度的点(在表2中用黑体作出标记)，为更加明确地显示锻件外表面温度变化趋势，用曲面图对锻件外表面展开后的温度分布进行表示。图6为含非对称裂纹轴类锻件不同轴向长度圆周上的温度分布曲面图。

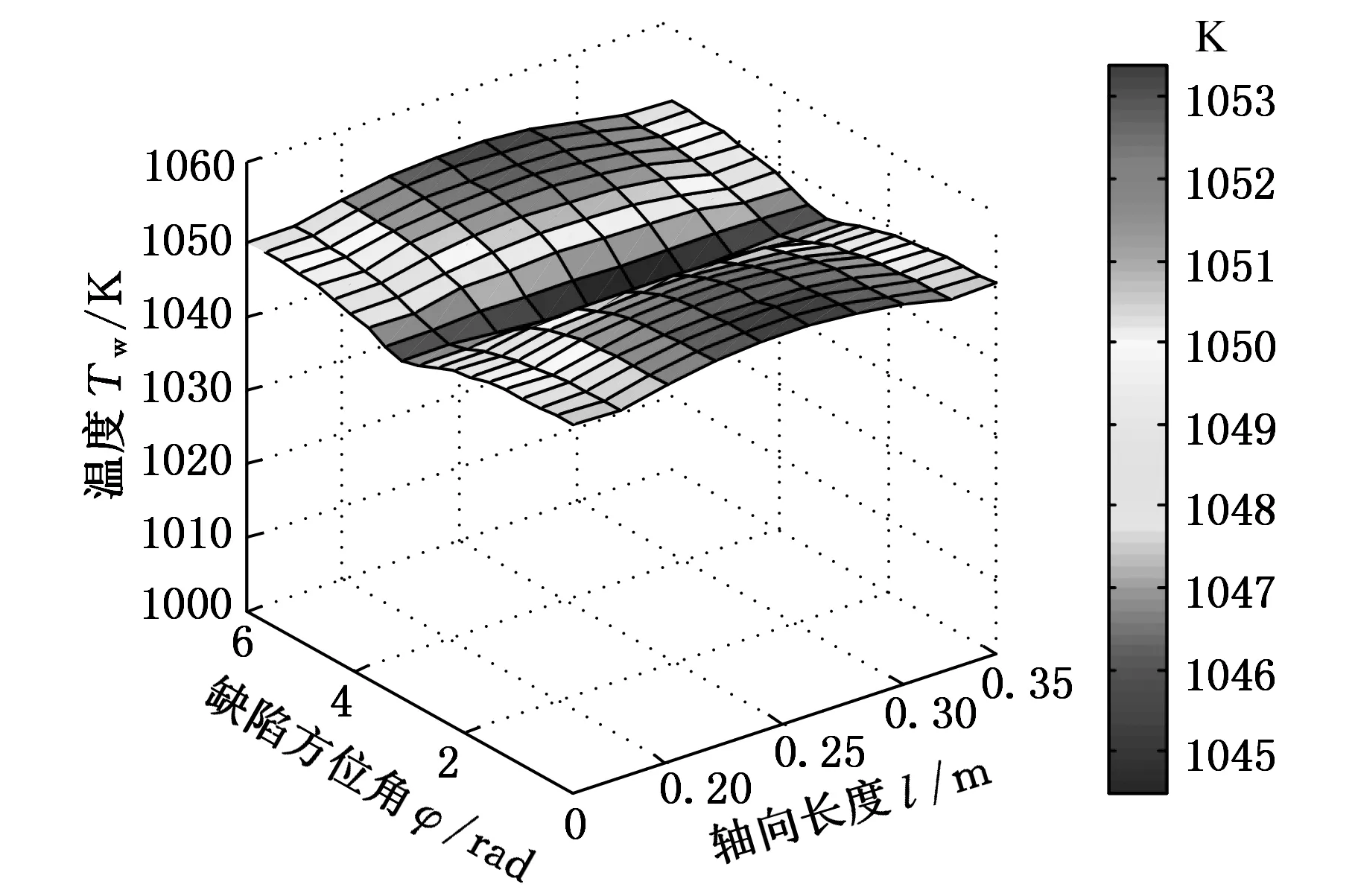
图6　含非对称裂纹轴类锻件不同轴向长度圆周上的温度分布曲面图

由图6的曲面图可以看出：锻件方位角4π/5 rad到6π/5 rad的轴向长度一段局部的温度下降明显，任意截面上的温度随角度的增加出现先降低再升高的趋势，由此可知此处锻件近表面位置有长条状缺陷。实际缺陷设定位置是在0.20 m到0.30 m之间，与实验结果基本一致，且采用热电偶测量的锻件外表面温度与采用红外热像仪测量的温度基本一致。

以上在理想条件下的仿真分析和实际条件下的实验结果基本一致，说明该模型能够通过对锻造过程中含裂纹轴类锻件外表面温度场分布规律进行分析来实现锻件内部缺陷的预判。

3　结束语

本文结合复合介质与非稳态热传导理论，采用集总参数法建立了对称与非对称裂纹条件下轴类锻件的温度场分析模型，利用建立的裂纹条件下轴类锻件的温度场分析模型得到了锻件外表面的温度场分布规律，通过对锻件外表面温度场分布规律进行对比分析，实现了对锻件内部状态的预判。实验证明了该模型的正确性，且通过此模型能够较准确、直观地反映锻件内部状态。因此，本文建立的裂纹条件下轴类锻件锻造中的温度场分析模型是可行的。

[1]赵俊伟, 陈学文, 史宇麟, 等. 大型锻件锻造工艺及缺陷控制技术的研究现状及发展趋势[J]. 锻压装备与制造技术,2009(4): 23-28.

Zhao Junwei, Chen Xuewen, Shi Yulin, et al. The Current Stage and Development Trend of Forging Technology and Defect Control for Heavy Forging[J]. China Metal Forming Equipment and Manufacturing Technology, 2009(4): 23-28.

[2]史小云, 付金宝, 王文盛, 等. 锻造温度对TC4-DT钛合金力学性能及显微组织的影响[J]. 中国有色金属学报, 2010, 20(1): 79-82.

Shi Xiaoyun, Fu Jinbao, Wang Wensheng, et al. Effect of Forging Temperature Mechanical Property and Microstructure of TC4-DT Titanium[J]. The Chinese Journal of Nonferrous Metals, 2010, 20(1): 79-82.[3]Lee H P. Thermal Stress Analysis of a Waste Storge Concrete[J]. Computer & Structures, 1996, 61(2): 197-224.[4]Lu X, Tervola P, Viljanen M. Transient Analytical Solution to Heat Conduction in Composite Circular Cylinder[J]. International Journal of Heat and Mass Transfer, 2006, 49(1/2): 341-348.

[5]关明, 付赟秋, 常志梁, 等. 大锻件锻造过程中温度场测定及其结果分析[J]. 锻压技术, 2012, 37(2): 6-9.

Guan Ming, Fu Binqiu, Chang Zhiliang, et al. Temperature Field Detection and Result Analysis of Heavy Forging during Forging Process[J]. Forging and Stamping Technology, 2012, 37(2): 6-9.

[6]张艳芹, 邵俊鹏, 倪世钱. 大尺寸静压轴承温度场数值模拟[J]. 中国机械工程, 2008, 19(5): 563-565.

Zhang Yanqin, Shao Junpeng, Ni Shiqian. Numerical Simulation of Temperature Field in Large Size Hydrostatic Bearings[J]. China Mechanical Engineering, 2008, 19(5): 563-565.

[7]张玉存, 付献斌, 刘彬, 等. 基于红外光谱大型筒类锻件热处理过程中温度场检测方法研究[J]. 光谱学与光谱分析, 2013, 33(1): 55-59.

Zhang Yucun, Fu Xianbin, Liu Bin, et al. Research on the Temperature Field Detection Method of Large Cylinder Forgings during Heat Treatment Process Based on Infrared Spectra[J]. Spectroscopy and Spectral Analysis, 2013, 33(1): 55-59.

(编辑袁兴玲)

Temperature Field Analysis Model of Shaft Forgings with Cracks during Forging

Fu Xianbin1Zhang Yucun2Dong Zhiming2Zhang Leiqiang2

1.Hebei University of Environmental Engineering,Qinhuangdao,Hebei,066102 2.Yanshan University,Qinhuangdao,Hebei,066004

Based on the unsteady heat conduction theory, a temperature field analysis model of shaft forgings with symmetric and asymmetric cracks was proposed. The shaft forgings with cracks were considered as composite media. According to lumped parameter method, the temperature field function of crack was obtained through solving governing equation of forgings with symmetric cracks. Then the temperature field function of asymmetric cracks was obtained by introducing correction factors. Moreover, the temperature field function of symmetric crack was regarded as the boundary conditions of heat conduction equation for shaft forgings with symmetric cracks. The temperature field function of asymmetric cracks was regarded as the boundary conditions of heat conduction equation for shaft forgings with asymmetric cracks. Therefore, combining with the corresponding boundary conditions, the temperature field analysis model of shaft forgings with cracks was established. The feasibility of this model was verified according to experimental results.

shaft forgings; crack; composite media; unsteady heat conduction theory; temperature field

2015-05-04

2016-06-17

河北省自然科学基金资助项目(E2014203070)；河北环境工程学院科研基金资助项目(BJ201603)

TB94

10.3969/j.issn.1004-132X.2016.16.021

付献斌，男，1985年生。河北环境工程学院信息工程系讲师。主要研究方向为尺寸和温度场检测。张玉存，男，1969年生。燕山大学电气工程学院教授、博士研究生导师。董志明，男，1988年生。燕山大学电气工程学院硕士研究生。张雷强，男，1988年生。燕山大学电气工程学院硕士研究生。