基于范数优化极限学习机的矿浆浓度预测

王　欢，姜昌伟，徐　鑫，孙为平，鲁鹏云，张德政

(1.鞍钢集团矿业公司，辽宁 鞍山 114001；2.北京科技大学计算机与通信工程学院，北京 100083；3.材料领域知识工程北京市重点实验室，北京 100083)



基于范数优化极限学习机的矿浆浓度预测

王欢1，姜昌伟2，3，徐鑫1，孙为平1，鲁鹏云1，张德政2，3

(1.鞍钢集团矿业公司，辽宁 鞍山 114001；2.北京科技大学计算机与通信工程学院，北京 100083；3.材料领域知识工程北京市重点实验室，北京 100083)

选矿过程中的矿浆浓度是一个重要的生产工艺参数，一般可以通过预测矿浆浓度来提高生产效率。由于矿浆浓度和其他的生产工艺参数往往非线性相关，这给矿浆浓度的预测带来了很大困难。本文针对此问题，基于极限学习机这一面向神经网络的新颖学习算法，提出了一种矿浆浓度预测新算法。首先，使用相空间重构方法对矿浆浓度数据进行预处理，从一维转换到多维。然后，使用基于L2范数的极限学习机算法(ELM-L2)建立时序预测模型，实现预测功能。围绕来自于某矿厂的真实生产数据进行了实验验证，结果显示，针对大规模的数据样本集，所设计的算法与传统神经网络预测算法相比，训练时间大约减少了30%，而预测精度大约提高了48%。实验结果表明了所设计预测算法的有效性。

极限学习机；相空间重构；矿浆浓度；预测

粗选过程的矿浆浓度是浮选过程中的重要工艺指标之一[1]。目前多数浮选过程都是通过离线化验检测来得到矿浆浓度，这需要较长的处理时间，导致调节落后。粗选过程中矿浆浓度的变化一般具有非线性特征，很难从化学反应机理上建立矿浆浓度的预测模型，因此，可考虑进行数据驱动建模[2-3]。根据矿浆浓度的具体生产数据，使用一些高效的神经网络算法建立预测模型，利用预测结果合理控制生产过程中各种原料的使用，同时根据预测值和实际值的比较来发现生产过程的变化和问题。

随着现代矿山自动化建设的推进及大数据信息化的快速发展，生产数据仓库存储了大量采集到的矿山生产经营管理数据，以及相关的各类外部数据[4]。通过分析采集到的矿浆浓度数据，基于BP神经网络等传统的机器学习算法，可建立时间预测模型，观察数据的变化趋势。虽然该方法取得了一定的成效，但在实际应用过程中，由于影响的因素过多，BP算法的预测效果变动较大，有时不甚理想，存在着预测精度不高和预测速度较慢等典型不足。

针对这些不足，本文考虑采用极限学习机(ExtremeLearningMachine，ELM)此类新算法，实现矿浆浓度的优化预测。ELM是近年来兴起的一类新颖的神经网络高效学习算法，它具有学习速度快、泛化能力强、可调节性能参数少等突出优势，在机器学习等领域得到了广泛的应用。与传统的神经网络学习算法相比，ELM在回归和分类等问题上，能够得到泛化能力更优的解，并且有着很快的训练速度。ELM已在很多特定领域，开展了数据分析应用[5-6]。由于经典的ELM是基于经验风险最小化原则实现的，它可能会在一些应用实例中产生过拟合现象，导致模型不够稳定，这给算法的实际应用带来了一定的挑战。为了克服传统ELM的这一不足，出现了一些改进的ELM算法，例如，基于核的ELM算法(Kernel-ELM)[7]、基于正则化的ELM算法(R-ELM)[8]、基于L2范数的ELM算法(ELM-L2)[7]等。这些算法在一定程度上能有效避免过拟合现象，并具有更好的鲁棒性和泛化能力。但是其中一些算法在实际应用中也有一些局限性。例如，这些改进的算法在一些小样本训练数据集中，都能达到很好的预测效果，但是随着样本数据量的逐步增加，Kernel-ELM和R-ELM算法的预测效果不甚理想，甚至会出现内存溢出的问题。因此，在样本数量比较大的情况下，这两类算法在计算实现上有一定困难。通过多次实验发现，ELM-L2算法的训练速度快，预测精度高，并且能够适应不同大小数据样本集的训练，基本不会出现内存溢出等计算问题。同时，采用矿山企业实际矿浆浓度数据进行的实验显示，与传统的BP算法相比，ELM-L2具有更高的预测精度。通过已经获得的数据，采用ELM-L2算法构建的学习网络，能够对相关未知数据进行预测，实验表明，预测效果比较理想。

1　相空间重构理论和极限学习机

1.1相空间重构理论

根据相空间重构理论，对于实际测得的一组时间序列数据{zi| i=1，2，…，p }，相空间中的相点个数为T=p-(r-1)τ，而重构后的相空间向量Zi(i=1，2，…，T)可表示为式(1)。

(1)

在这里，对于选择的r和τ，在测得的时间序列数据{zi| i=1，2，…，p }中，存在一个嵌入时间窗Γ，使得zi和zi+Γ所构成的相空间轨迹相对规则[9]。

1.2极限学习机

极限学习机(ELM)作为一种简单且有效的神经网络学习算法，最早被提出用来训练单隐层前馈神经网络。在该网络中，输入层和隐含层间的权值矩阵以及隐含层节点的偏置可以随机初始化，而不需要像传统学习算法那样进行迭代更新。所需计算的只有隐含层和输出层的权值矩阵，而该矩阵则可通过求广义逆矩阵的方法求得。

这里，设定有N个训练数据{xi，ti} (i=1，2，…，N)，其中，xi是d维的训练样本，ti是m维的输出向量。ELM算法的整体结构如图1所示[5]。图中，L是隐含层节点的数目，wj是隐含层中第j个节点与输入层之间的权重向量，bj是隐含层第j个节点的偏置。wj和 bj一旦随机初始化后就不再改变。y是ELM算法中的的输出向量，对于第i个样本，隐含层的输出可以表示为zi，见式(2)。

(2)

图1　ELM的应用框架

对于所有的训练数据而言，神经网络的输出函数可以表示为：Hβ=T，其中，H为隐含层的输出矩阵，可以表示为式(3)。另外，β为输出权重，可以表示为式(4)。T是输出向量，可以表示为式(5)。

(3)

(4)

(5)

2　基于范数优化极限学习机的矿浆浓度预测

传统的预测算法(如BP神经网络算法)往往存在训练速度慢和预测精度不高等不足，在进行矿浆浓度预测时，很难满足实际要求。ELM是一种非常简单的机器学习算法，它有着很好的泛化能力，并且学习速度远远快于传统的神经网络学习算法。考虑到经典ELM的实现主要基于经验风险最小化原则，可能产生一个比较复杂的学习模型。因此，可以通过引入ELM-L2这一改进算法，在一个统一框架中进行优化学习处理。实际上，仿真结果也显示，ELM-L2算法的预测精度明显优于BP算法。在这里，基于L2范数ELM的数学模型可描述为式(6)[7，10]。

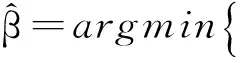
(6)

式中，ξ表示L2范数的正则化系数。式(6)能产生一个闭合解，可表示为式(7)。

厚责于己，能实现自身素质的提升。责己有利于我们及时地发现自身的不足并迅速改正，进而逐渐提高自我的修养，达到“知明而行无过”的最终目标。

(7)

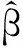
(8)

(9)

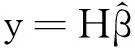
(10)

式中，I是一个单位矩阵。引入L2范数的ELM改进算法是基于结构风险最小化的原则，具有更好的泛化能力和更强的鲁棒性。

通过引入L2范数到传统的ELM中，克服了传统ELM的一些缺点。ELM-L2算法的学习步骤可以总结如表1所示。

表1　ELM-L2算法的执行步骤

针对矿浆浓度预测问题，这里基于范数优化极限学习机ELM-L2求解算法的实现框架如图2所示。

图2　基于范数优化极限学习机的矿浆浓度预测实现框架

3　实验结果和分析

为了验证预测算法的有效性，基于国内某个矿山企业的矿浆浓度真实数据，开展了如下的测试实验。算法运行在IntelRRCoreTMi3，2.13GHzCPU的计算环境中。首先，整合收集到的数据。数据是按一个固定的时间间隔来采集的，其中有效的数据被控制在40～50之间。在实验进行之前，首先分析了所采集数据的变化特征。图3是基于采集到的20000多个数据绘制的矿浆浓度拟合图，由于数据是等时间间隔获得的，所以拟合图能够在一定程度上说明数据的变化趋势。从图3可以看出，20000多个数据分布波动相对比较大，整体呈现先上升再下降的趋势，但在局部上，数据的分布还是比较稳定的。由于数据的分布呈现比较明显的非线性特征，传统的预测方法较难建立一个适应于此情况的动态预测模型，而数据驱动下的神经网络优化预测算法则对处理此类非线性问题有一定优势，尤其是本文讨论的ELM-L2算法，有着很好的泛化能力。

在预测问题的研究中，一般用均方根误差(RootMeanSquareError，RMSE)作为评价标准，RMSE的值越小，说明预测的结果越准确，误差越小。RMSE的计算公式见式(11)。

(11)

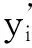
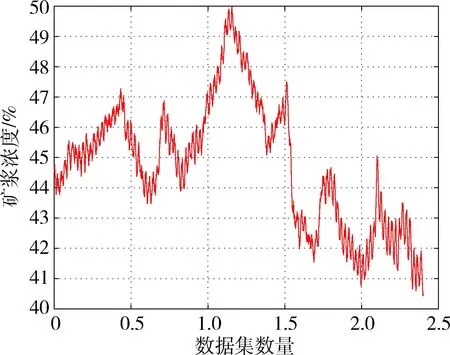
图3　矿浆浓度数据变化趋势

另外，根据对所获得的矿浆浓度样本数据集的分析，采用大小为3000和7000的样本进行预测实验比较合适。这里主要完成了时序预测实验。这里的时序序列是指按照时间的顺序，将事情变化发展的过程记录下来，所构成一个特定序列。通过观察和研究时序序列，找寻其变化发展的规律，以预测将来的走势。本实验主要根据时序序列，研究矿浆浓度的变化发展趋势，找寻矿浆浓度的变化规律，另外，还通过对比分析ELM-L2和传统的神经网络算法BP的训练学习效果，验证ELM-L2算法在预测精度方面的优势。

因为这里获得的是时序序列的数据，如果不对数据进行预处理，很难获得理想的训练学习效果，因此，在使用BP和ELM-L2算法进行实验之前，使用文献[9]中的相空间重构方法对数据进行了预处理，将一维数据转为多维数据。采用同一数据集，使用不同的时间延迟τ和嵌入维数r进行实验，当时间延迟τ为8，嵌入维数r为2时，预测精度最高。所以，在下面的实验中，将时间延迟τ设为8，嵌入维数r设为2。对经过相空间重构预处理后的矿浆浓度数据集，分别利用ELM-L2和BP算法进行训练，得到相应的预测学习实验结果。图4是针对3000个测试样本的矿浆浓度时序预测结果，其中ELM-L2的预测曲线更接近真实值曲线，而BP的预测曲线波动较大，与真实值差别较大。图5是针对7000个测试样本的时序预测结果，通过图5可以看出，相比3000的样本进行实验时，ELM-L2的预测精度更高。这说明，在本文数据驱动下的神经网络优化预测算法应用中，数据样本越多，预测效果越好，这与前文中的理论分析是一致的。同时，对比BP算法的预测效果，当样本数量达到7000时，预测精度很差。这主要是因为BP算法中的神经网络结构固定，其在线反复迭代训练学习机制，对样本数据增加后的适应效果不佳，致使预测精度下降明显。

本实验分别使用3000和7000个样本进行测试。首先，通过重构后，将20个样本作为测试集，其余数据作为训练集。表2显示了，针对不同数量的样本集，ELM-L2和BP两种算法的测试精度和训练时间。

通过上述针对不同大小样本数据集进行的实验，可以看出，在不同数量的训练样本下，ELM-L2的预测精度都比BP的预测精度高，而且ELM-L2训练时间明显更短。另外，通过使用不同数量的样本进行实验，还可以发现，当训练样本数量较小时(即低于3000时)，ELM-L2和BP算法的预测精度都可以满足实际的要求。而随着训练样本数量的增加，ELM-L2能达到更好的预测精度，BP算法的预测精度反而下降，不能满足实际预测精度的要求。

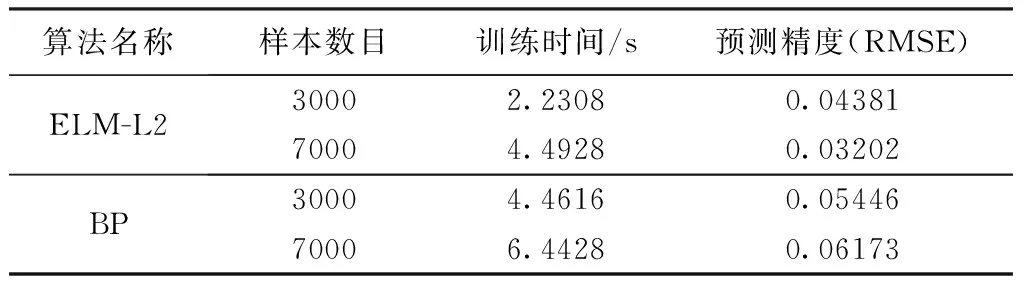
表2　ELM-L2和BP算法的训练时间和测试精度

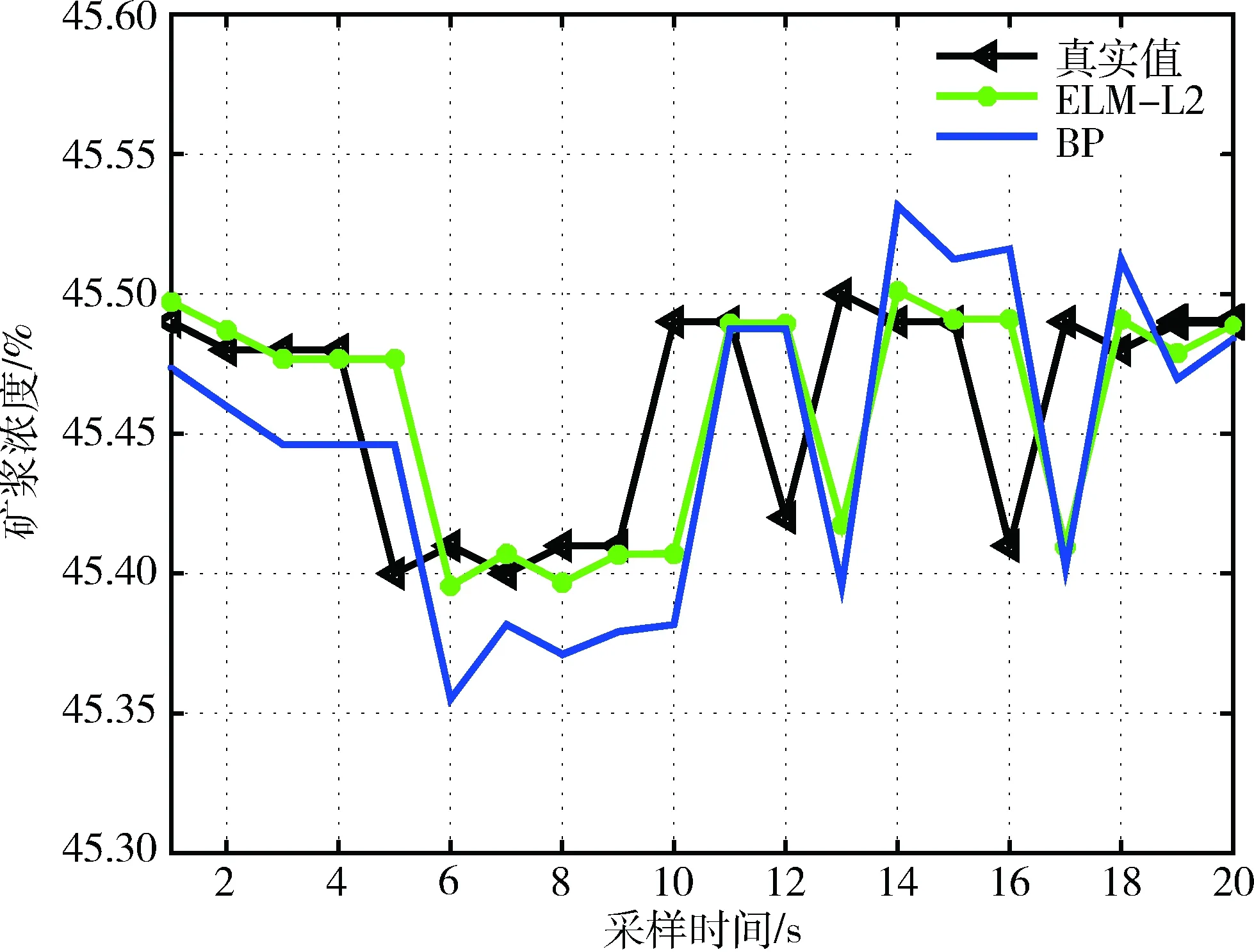
图4　矿浆浓度时序预测结果(3000个测试样本)

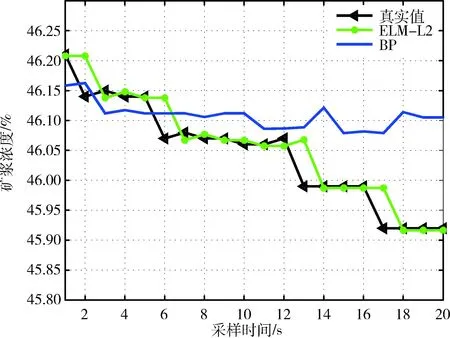
图5　矿浆浓度时序预测结果(7000个测试样本)

4　结　论

为了预测矿浆浓度的变化趋势，并总结其变化规律，本文利用矿山数据仓库中的历史数据，提出了数据驱动下基于ELM-L2算法的矿浆浓度预测神经网络学习新方法，建立了矿浆浓度的时序预测学习模型。本文中提出的ELM-L2神经网络学习预测模型结构简单，泛化能力强，收敛速度快，能获得较好的预测精度。结合某矿山的实际生产数据，进行了实验验证，结果显示，针对大规模的数据样本集，本文中提出的方法与传统的BP神经网络预测算法相比，所需的训练时间大约减少了30%，而预测精度则大约提高了48%，有效验证了文中方法的高效性。通过基于ELM-L2的选矿生产指标预测方法，可发现矿浆浓度的变化规律，从而能够合理配置选矿过程中的其他原料。另外，通过预测矿浆浓度的变化趋势，还可以发现选矿过程中可能出现的问题，在一定程度上保证安全生产。在今后的工作中，将进一步结合矿山生产中的其它工艺数据，进行方法的应用验证。

[1]刘长鑫，丁进良，姜波，等.选矿过程精矿品位自适应在线支持向量预测法[J].控制理论与应用，2014，31(3)：386-391.

[2]薄洪光，张书冉，刘晓冰，等.支持钢铁企业产能时序预测的数据同化方法[J].计算机集成制造系统，2011，17(6)：1298-1307.

[3]Tucker P.The influence of pulp density on the selective grinding of ores[J].International Journal of Mineral Processing，1984，12(4)：273-284.

[4]Blazquez G，Hoces M C，Castro F H.Influence of pulp density and cell size in minerals flotation[J].Afinidad Revista De Química Teórica Y Aplicada，2002，59(500)：415-420.

[5]Huang G B，Song S，You K.Trends in extreme learning machines：a review[J].Neural Networks，2015，61：32-48.

[6]Luo X，Chang X H，Ban X J.Regression and classification using extreme learning machine based on L1-norm and L2-norm[J].Neurocomputing，2016，174：179-186.

[7]Huang G B，Zhou H，and Ding X.Extreme learning machine for regression and multiclass classification[J].IEEE Transactions on Systems，Man，and Cybernetics，Part B：Cybernetics，2012，42(2)：513-529.

[8]Deng W Y，Zheng Q H，Chen L.Regularized extreme learning machine[C]//Proceedings of IEEE Symposium on Computational Intelligence and Data Mining，2009：389-395.

[9]Zhang W，Ma Y，and Yang G.Study on parameter selection of phase space reconstruction for chaotic time series[J].Advances in Information Sciences and Service Sciences，2012，4(2)：67-77.

[10]Hoerl A E，Kennard R W.Ridge regression：biased estimation for nonorthogonal problems[J].Technometrics，1970，12(1)：55-67.

A prediction algorithm for pulp concentration using norm-optimized extreme learning machine

WANGHuan1，JIANGChang-wei2，3，XUXin1，SUNWei-ping1，LUPeng-yun1，ZHANGDe-zheng2，3

(1.AnsteelMining，Anshan114001，China；2.SchoolofComputerandCommunicationEngineering，UniversityofScienceandTechnologyBeijing，Beijing100083，China；3.BeijingKeyLaboratoryofKnowledgeEngineeringforMaterialsScience，Beijing100083，China)

Pulpconcentrationasoneofthemostimportantproductionparametersplaysanimportantroleintheoreproduction.Generally，theproductionefficiencycanbeimprovedbyapredictionforpulpconcentration.Sincetherearesomenonlinearrelationshipsbetweenthepulpconcentrationandotherproductionparameters，itimposesverychallengingobstaclestoaddressthisissueofprediction.Anovelpredictionmethodisproposedinthispaperthroughtheuseofextremelearningmachine(ELM)thatisaneffectivelearningalgorithmdevelopedforneuralnetwork.Firstly，thepulpconcentrationdataispreprocessedbythephasespacereconstructionmethod，andthetimeseriespredictionmodelisadjustedfromonedimensiontomultipledimensions.Secondly，animprovedELMalgorithmusingL2norm(ELM-L2)isdevelopedtoimplementtheprediction.Theexperimentsareconductedwithareal-worldproductiondatasetfromamine.Comparedwiththetraditionalpredictionmethodusingneuralnetwork，theproposedapproachcanreducethetrainingtimeby30%andimprovethepredictionaccuracyby48%foralarge-scaledataset.Theexperimentalresultsshowtheeffectivenessoftheproposedalgorithm.

extremelearningmachine(ELM)；phasespacereconstruction；pulpconcentration；prediction

2015-12-08

中央高校基本科研业务费专项资金资助项目资助(编号：FRF-BD-15-013A)

王欢(1971-)，男，高级工程师，现任鞍钢集团矿业公司信息开发中心经理，主要从事矿山信息化方面的研究与开发工作。E-mail：info_engineering@163.com。

张德政(1964-)，男，教授，博士研究生导师，北京科技大学计算机与通信工程学院副院长，材料领域知识工程北京市重点实验室主任，主要从事人工智能与知识工程的研究工作。E-mail：dzzhzd@126.com。

TP3，TD9

A

1004-4051(2016)08-0112-05