圆柱绕流气动噪声数值分析

顾信忠，李舜酩



圆柱绕流气动噪声数值分析

顾信忠1,2，李舜酩1

(1. 南京航空航天大学能源与动力学院，江苏南京210016; 2. 南京航空航天大学金城学院车辆系，江苏南京211156)

为了快速预测刚性圆柱绕流的气动噪声，研究了一种将离散涡方法(DVM)和涡声理论结合起来计算低马赫数、高雷诺数流场气动噪声的方法。首先用Oseen粘性涡模型改进了离散涡方法并模拟了圆柱绕流，分析结果与实际情况相符。根据流场计算的结果，应用涡声理论进一步计算了远场的声压。测点的总声压级与实验值及其他数值计算结果都比较吻合。最后绘制了声场的指向性特性曲线，表明圆柱绕流声场明显的偶极子特性。

气动噪声；圆柱绕流；离散涡方法；涡声理论；Oseen涡

0 引言

圆柱体绕流产生声音是一种非常普遍的现象。产生的机理包括：流体与圆柱壁面的相互作用使圆柱产生振动，振动的圆柱排开流体就形成了单极子声源；当旋涡从圆柱表面交替脱落时，会在圆柱表面产生正负环量，柱面附近区域因此产生周期性压力波动，从而形成了偶极子声源；圆柱表面边界层中的涡旋和脱落的涡旋会因湍流应力而不断衰减，此湍流应力就是四极子声源[1]。

圆柱绕流产声问题在航空航天、航海、风工程等实际工程中非常具有代表性，因此众多的学者对此进行过深入研究，所采用的方法大致可以分为声类比方法和直接数值模拟方法两大类。

文献[2]采用有限体积法分别求解二维、三维可压缩平均雷诺数N-S方程，对马赫数为0.2、雷诺数为100～5000000的圆柱绕流进行了数值分析，并用Lighthill声类比方法获得了远场声信息。文献[3]用大涡模拟方法模拟了雷诺数为50000～90000的圆柱绕流湍流流场，提取声源的强度和分布信息后，用FW-H方程的积分外推法计算了远场气动噪声，研究了圆柱绕流气动噪声的声场特性。文献[4]则采用高精度的空间和时间离散算法直接求解N-S方程（DNS方法），计算结果可以清晰显示声波的产生和传播过程而不受马赫数和雷诺数的限制。文献[5]同样采用DNS方法分析了马赫数为0.2、雷诺数为150时圆柱绕流的气动噪声，着重研究了涡与声压之间的内在关系。

上述两类方法都需要采用非常细密的网格和高精度算法对流场进行准确的计算，因此需要大量的存储空间和很长的计算时间。本文则是基于离散涡方法和涡声理论，采用Oseen粘性涡模型，研究了可快速预测绕流产生气动噪声的方法。

1 流场模拟

1.1 离散涡方法

离散涡方法通过计算涡量，求解Navier-Stokes方程，以拉格朗日方式跟踪脱落涡的运动轨迹，恰能满足流场涡声计算的需要，因此本文采用离散涡方法模拟流场。

离散涡方法的基本思路是将流场分成有旋和无旋两部分，有旋部分主要集中在柱面的边界层和分离后的剪切层，并认为两者都是薄薄的连续涡层，可用离散的涡元来模拟，并将其置于无旋流场中，通过计算离散涡元之间相互作用和演化实现对流场的快速模拟。当柱面的轴向尺寸远大于其断面尺寸时，则可用二维离散涡方法模拟流场[6-7]，如图1所示。

1.2 涡模型选择

当两个点涡接近时产生诱导速度非常大，与实际情况不符，因此很多文献[8-9]采用Rankin涡模型进行光滑处理。但是涡声与涡量的变化率有关，而Rankin涡的涡量是恒定的，因此本文采用的是Oseen粘性涡模型，其周向速度为[10]

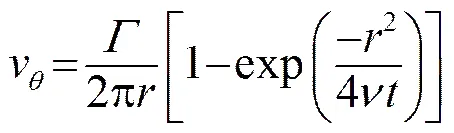
其中：为涡的环量；为离涡核中心的距离；为流体的运动粘性系数；为计算时间。

1.3 离散涡方法计算流程

1.3.1 边界层涡量的确定

将圆柱面用若干个等长首尾相连的直线段来离散，直线段的端点布置适当强度的涡元，称为涡点，直线段的中点称为控制点。根椐Dirichet边界条件——物面的切向速度为零，要求任意控制点处的流速与涡元产生的诱导速度相应[11]，即

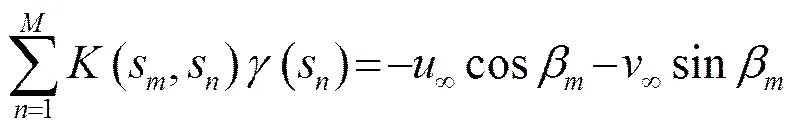
其中：(s,s)为相关系数，表示s处单位强度点涡在s控制点处产生的诱导速度；(s)为s涡点处涡的强度；u、v分别为来流的速度分量；β为控制点s的位矢与水平方向的夹角。写成矩阵形式为

(3)

求解该线性方程组即可得到各涡点处涡元的强度。

1.3.2 涡的脱落

边界层中的涡会不断从柱面分离进入尾流，本文采用固定分离点的方式产生脱落涡，即预先在物面上确定几个涡点产生脱落涡。根据库塔(Kutta)条件可确定初生脱落涡的环量为[12]

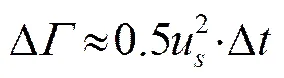
其中：u为相应涡点处边界层外的流速；为计算的时间步长。

初生脱落涡的平均对流速度为[13]

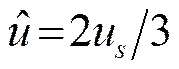
1.3.3 涡的对流

已知二维不可压缩无粘流场中所有涡元（包括边界层中的涡元和脱落涡）的强度和位置，则可用Biot-Savart公式计算出流场中任意点处的诱导速度为

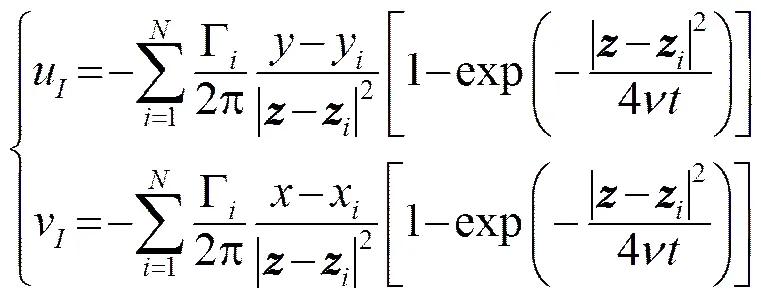
式中：为涡元在复平面中的位矢；x、y分别为其水平和竖直分量。

将诱导速度与来流速度叠加就可以得到流场中任意位置的实际速度为

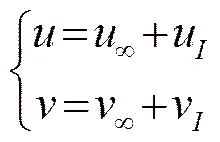
假设在时刻涡元的位置为()、()，则可得到涡元对流的计算公式为

(8)

其中：和为涡元因粘性扩散产生的运动，可采用随机走位估算[14]：

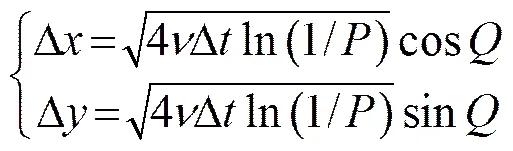
式中：和分别是(0，1)和(0，2π)区间内两个相互独立的随机数。97

1.3.4 涡的合并与镜像

实际情况下，当两涡元之间距离足够小时，就会因涡核被破坏而发生合并。于是Spalart提出了涡的融合机制[15]，即认为当两个涡元满足一定条件时，就被合并成一个涡元。

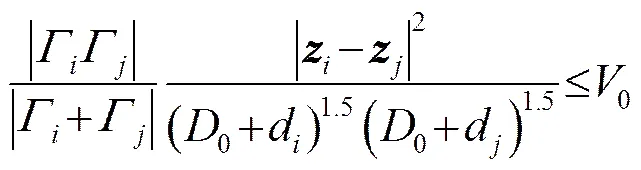
式中：0和0都是控制参数；0控制圆柱附近的涡元数目；0控制流场中涡元总数。合并后新涡元的位置和环量分别为：

， (11)

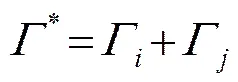
当涡元运动到圆柱内部时，文中采用镜像的方法将其强制移到圆柱外部。

1.3.5 作用在圆柱上的力

流体流经圆柱表面时会产生相互作用，圆柱上的作用力可用布拉休斯公式计算，将该作用力在竖直方向和水平方向进行分解，并除以0.5∞2进行无量纲化，即可得到圆柱上的升力和阻力系数[12]：

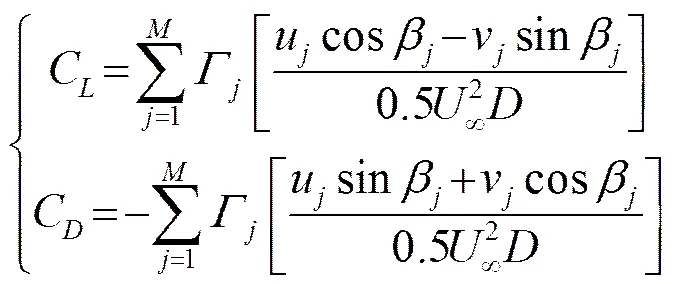
式中：Г、u、v、β分别为第涡点处的涡的环量、柱面的切向速度、法向速度和方位角；∞为平均来流速度；为圆柱直径。

1.4 流场仿真结果

本文以实验验证的模型[16]为研究对象，圆柱直径为19 mm，空气流速为69.2 m/s，此时雷诺数为Re≈90000，马赫数约为0.2。圆柱面上均匀布置了40个涡点，其中5个为预定的脱落点，如图1所示。设置计算时间步长为10-5 s，图2是=0.02 s时的涡元分布图，此时流场中有3600多个脱落涡元，可见从圆柱脱落的涡并没有形成稳定的卡门涡街，而是扩散到尾流区很宽的范围内形成了紊流，与实际情况相符。

升力系数和阻力系数如图3和图4所示，因为在计算过程中存在大量的涡元合并与镜像，使得升力系数的变化范围非常大，流场稳定后升力系数在0值的上下等幅振荡。阻力系数的时间平均值约为1.52，比实验值1.32[16]大15.2%，比文献[17]中的大涡模拟结果1.47大3.4%，如表1所示。说明文中采用的离散涡方法能够较为准确地模拟圆柱绕流。

表1 圆柱绕流平均阻力系数(Re≈90000，马赫数≈0.2)

2 声场计算

2.1 涡声理论

根据气动声学理论[18]，在大雷诺数、低马赫数无粘三维流场中，运动涡元产生的远场声压为

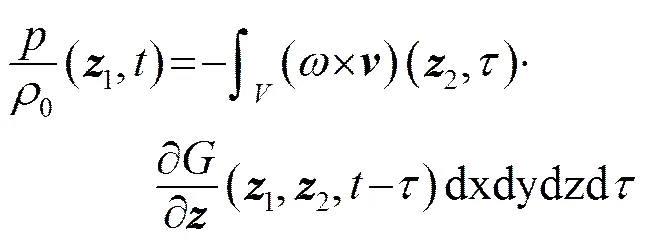
式中：0为流体密度；为涡量；为涡的运动速度；为声源发射声波的时刻；为紧致格林函数；1为观测点的位矢；2为声源即涡的位矢。

若柱体的轴向尺寸远大于其断面尺寸，可在二维中计算涡声[18]，此时紧致格林函数为

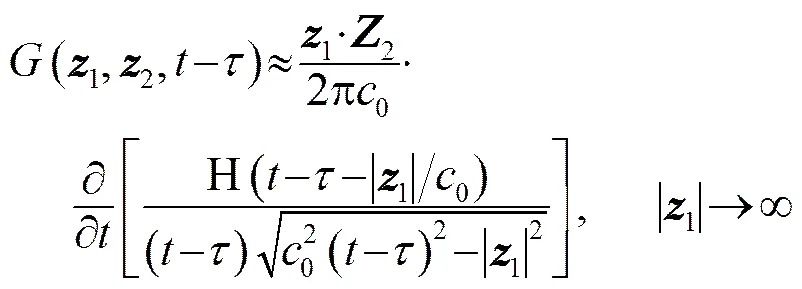
其中：2为基尔霍夫矢量；0为声波传播速度；H(.)为Heaviside广义函数。将式(15)代入式(14)即可得到二维流场的声压为

(16)

分别将=1、2代入上式，就可以得到柱体上脉动升力和阻力产生的远场声压。若声场中的柱体为圆柱，则基尔霍夫矢量为

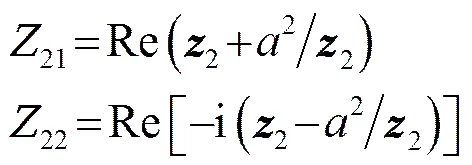
2.2 声场计算结果

2.2.1 声压

为了与实验值比较，与文献[16]相同，在远场取三个测量点，坐标分别为：测量点1(0.665，0)、测量点2(0，-0.665)、测量点3(0，2.432)，如图5所示，各测点的声压如图6所示。

对测点的声压信号进行快速傅里叶变换，得到频域下的声压规律，利用式(18)计算各测点的声压级为

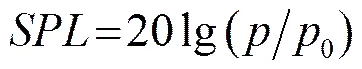
(a)

(b)

图6 各测点声压

Fig.6 The time-histories of sound pressures at different testing points

测量点声压级的频谱特性曲线如图7所示，噪声频率分布范围很宽，且测点的声压级在750 Hz左右有明显的峰值，与实际流场中涡从柱面脱落的周期相应。

还可进一步计算各测点的总声压级：

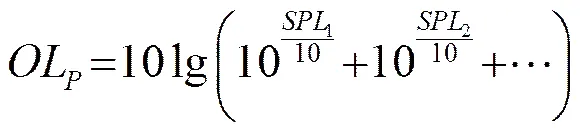
得到测量点1总声压级为118.52 dB，而实验测量值为117 dB[16]，误差仅为1.3%，比大涡模拟的结果115.72[3]高2.4%，比115.16 dB[17]高2.9%；测量点3 总声压级的仿真值为113.74 dB，实验测量值为100 dB，误差为13.7%，比大涡模拟的结果104.52 dB[3]高8.8%，比103.89 dB[17]高9.5%，如表2所示。

表2 圆柱绕流总声压级(Re≈90000，马赫数≈0.2)

Tabie 2 Overall sound pressure levels at different testing points (Re≈90000, Mach number≈0.2)

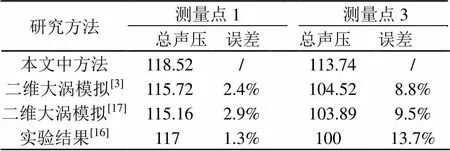
研究方法测量点1 测量点3 总声压 误差总声压 误差 本文中方法118.52/ 113.74/ 二维大涡模拟[3]115.722.4% 104.528.8% 二维大涡模拟[17]115.162.9% 103.899.5% 实验结果[16]1171.3% 10013.7%

测点1、3的总声压级均大于实测值及大涡模拟的结果，可能产生误差的原因包括以下几个方面：第一，在仿真过程中用大量的离散涡元模拟边界层和剪切层中的连续涡层，使得声压信号中的高频成分偏高；第二，为了编程方便，文中将边界层的离散涡元直接布置在物面上，而当声源靠近物面时，对外辐射的声压较大；第三，在计算涡元对流时采用的是精度较低的一阶差分格式，可能对计算结果存在一定的影响。总体来看，仿真预测结果是较为可信的。

2.2.2 指向性特性

图8是声场在=0.019 s、=0.0195 s和=0.02 s时的辐射特性曲线，声压最大辐射值都在垂直于来流的轴线上，指向性与偶极子声源的指向性相近，说明圆柱绕流的气动噪声主要是由偶极子声源引起的。在平行于来流方向仍有一定的声辐射，这是由作用在圆柱上的阻力周期性波动以及涡元粘性衰减的四极子声源共同作用的结果。

=0.019

=0.0195

3 结论

(1) 采用离散涡方法对二维圆柱绕流流场的模拟结果显示，流场图与实际情况相符，升力系数和阻力系数的计算值都与实验结果较为吻合，模拟结果是可信的。

(2) 圆柱绕流产生的气动噪声的峰值频率与涡的脱落频率相应，总声压级与实验值及大涡模拟仿真结果比较吻合，声场的辐射特性与实际情况相符，声场的计算结果是比较准确的。

(3) 由于采用大量的离散涡元模拟边界层和剪切层的连续涡层，获得的声信号中的高频成分偏高。

(4) 采用离散涡方法和涡声理论相结合的方法，对声场进行快速预测的方法是可行的。

[1] 张强. 气动声学基础[M]. 北京: 国防工业出版社, 2012.

ZHANG Qiang. Foundation of Acoustics[M]. Beijing: National Defense Industry Press, 2012.

[2] COX J S, Brentner K S, Rumsey C L. Computation of vortex shedding and radiated sound for a circular cylinder: subcritical to transonic Reynolds numbers[J]. Theoret. Comput. Fluid Dyn, 1988, 12(4): 233-253.

[3] 龙双丽, 聂宏, 许鑫. 不同雷诺数下圆柱绕流气动噪声数值模拟[J]. 声学技术, 2011, 30(2): 111-116.

LONG Shuangli, NIE Hong, XU Xin. Numerical simulation of noise induced by flow around a cylinder at different Reynolds number[J]. Technical Acoustics, 2011, 30(2): 111-116.

[4] Mitchell B E, Lele S K, Moin P. Direct computation of the sound generated by vortex pairing in an axisymmetric jet[J]. J. Fluid Mech, 1999, 383(6): 113-142.

[5] Inoue O, Hatakeyama N. Sound generation by a two-dimensional circular cylinder in a uniform flow[J]. Journal of Fluid Mechanics, 2002, 471(01): 285-314.

[6] MUSTTO A A, Hirata M H, Bodstein G C R. Discrete vortex method simulation of the flow around a circular cylinder with and without rotation[J]. AIAA paper, 1998, 98-2409: 59-69.

[7] Etoh F, Kamemoto K, Matsumoto H, et al. Numerical simulation of flow around a rotary oscillating foil with constant amplitude angle by use of the vortex method[C]//Proc. 11th Symp. on CFD, Tokyo, 1997: 385-386.

[8] 潘岩松. 高层建筑二维流场的离散涡方法数值模拟[D]. 武汉: 华中科技大学, 2004.

PAN Yansong. Numerical simulation of two-dimensional flow past a tall building using a discrete vortex method[D]. Wuhan: Huazhong University of Science & Technology, 2004.

[9] 徐晓亮, 黄海明, 章梓茂. 烧蚀环境下的圆柱绕流计算模型[J]. 空气动力学学报, 2011, 29(2): 170-176.

XU Xiaoliang, Huang Haiming, Zhang Zimao. Numerical models for flow past a cylinder in the ablation environment[J]. Acta Aerodynam Ica Sinica, 2011, 29(2): 170-176.

[10] Schaefer J W, Eskinazi S. An analysis of the vortex street generated in a viscous fluid[J]. J. Fluid Mech.,1959, 6(2): 241-260.

[11] Lewis R I, Vortex element methods for fluid dynamic analysis of engineering systems[M]. Cambridge University Press, 2005.

[12] Sarpkaya T, Shoaff R L. An inviscid model of two dimensional vortex shedding for transient and asymptotically-steady separated flow over a cylinder [J]. AIAA Paper, 1979, 79-0281: 1-9.

[13] 童秉纲, 夏南, 李潜.物体绕流的离散涡方法[J]. 力学进展, 1985, 15(3): 318-328.

TONG Bingang, XIA Nan, LI Qian. Discrete Vortex Method in external flow problems [J].Advances in Mechanics, 1985, 15(3): 318-328.

[14] 陈伟, 宗智. 二维圆柱绕流的离散涡数值模拟[J]. 舰船科学技术, 2010, 32(5): 111-115.

CHEN Wei, ZONG Zhi. Numerical simulation of two- dimensional flow around circular cylinder using discrete vortex method[J]. Ship SciencE and Technology, 2010, 32(5): 111-115.

[15] SPALARTR S, LEONARD A, BAGANOFF D. Numerical simulation of separated flows[D]. Stanford University, California, 1983.

[16] Revell J D, Prydz R A, Hays A P. Experimental study of aerody­namic noise vs drag relationships for circular cylinders[J]. Anz Journal of Surgery, 1978, 16(6): 889-897.

[17] YANG Dangguo, LI Jianqiang, LIU Jun. Analysis on physical mechanism of sound generation inside cavities based on acoustic analogy method[J]. Journal of Fluid Dynamics, 2013, 3(1): 23-31.

[18] HOWE M S. Theory of vortex sound [M]. Cambridge Texts in Applied Mathematics, 2002.

Numerical analysis of noise induced by flow around a cylinder

GU Xin-zhong1,2, LI Shun-ming1

(1. College of Energy and Power Engineering,Nanjing University of Aeronautics &Astronautics, Nanjing 210016,Jiangsu, China；2. Department of Vehicle Engineering, Nanhang Jincheng College, Nanjing211156, Jiangsu,China)

The method of combination of Discrete Vortex Method (DVM) and the theory of vortex sound are used to predict two-dimensional far field noise induced by flow around a cylinder. Firstly, the field of flow around a cylinder is simulated using the Oseen vortex model. The simulation results are in agreement with experimental data. Based on the simulation results, the characteristic of the acoustic field is studied. The overall sound pressure levels of receivers also accord wellwith both experimental data and other numerical simulation results. The polar diagrams of the aeroacoutic pressure are plotted. And the dipolar nature of the generated sound is confirmed.

aerodynamic noise; flow around a cylinder; Discrete Vortex Method(DVM); theory of vortex sound; oseen vortex

TB533

A

1000-3630(2016)-02-0095-06

10.16300/j.cnki.1000-3630.2016.02.003

2015-04-10;

2015-06-10

顾信忠(1980－), 男, 江苏仪征人, 博士研究生, 研究方向为气动噪声预测与控制技术。

顾信忠, E-mail: guxingzhong007@126.com