基于光纤矢量水听器的浅海噪声矢量场特性研究

朱良明，李风华，陈德胜



基于光纤矢量水听器的浅海噪声矢量场特性研究

朱良明1,2，李风华1，陈德胜1

(1. 中国科学院声学研究所声场声信息国家重点实验室，北京100190; 2. 中国科学院大学物理学院，北京100049)

基于简正波理论分析了浅海噪声矢量场声压和质点振速的强度特性，仿真了浅海声压和质点振速的噪声强度在深度和频率上的变化特性，噪声矢量场强度特性仿真结果与实验测量结果一致。针对声场测量的有效性，给出了加速度通道自噪声谱级和灵敏度必须满足的关系式，并提出了降低自噪声对接收系统影响的两种措施。最后分析并对比了系统自噪声谱级和海洋环境噪声谱级，结果表明，声压通道的自噪声比环境噪声谱级低20 dB左右，Y通道和Z通道的自噪声比环境噪声低3.5 dB以上, X通道的自噪声谱级在200 Hz附近与环境噪声谱级最为接近，约比环境噪声低1.5 dB。

光纤矢量水听器；噪声矢量场；系统自噪声；海洋环境噪声；灵敏度

0 引言

矢量水听器因其能够共点同步测量空间某点处的声压和质点振速而在水声领域倍受关注[1]，声压与振速联合信息处理可以更好地获取波导参数和声源位置信息[2]。矢量水听器具有良好的低频指向性和抗各向同性干扰能力，能够获得一定的空间增益。矢量水听器这些优点使其在低频弱目标探测领域倍受青睐。与压电水听器相比，干涉型光纤矢量水听器具有灵敏度高、信号损耗小、稳定性高的优点。应用现有成熟的光纤通讯技术，光纤矢量水听器可以方便地组建水下光纤阵列和大范围光纤传感器网络。

随着矢量水听器在水声领域的应用，国内外学者进行了矢量声场预报[3-4]、矢量声场传播特性[5-6]、噪声矢量场特性[7-11]等方面的研究，同时还进行了矢量水听器目标测向[12-15]和匹配场反演与定位[16]等应用方面的研究。

为实现矢量水听器对声场的有效记录，需严格控制系统自噪声强度，并应用减振和流噪声抑制技术降低系统低频振动干扰和流噪声。海洋环境噪声作为常见的背景干扰，研究噪声矢量场特性对矢量水听器应用具有重要意义。

本文首先结合矢量水听器灵敏度特性讨论了声压通道和质点振速通道的系统自噪声特性。针对声场测量的有效性，给出了加速度通道自噪声谱级和灵敏度所需满足的关系式，并提出降低自噪声对接收系统影响的两种措施。然后利用简正波理论分析了浅海噪声矢量场声压和质点振速的强度特性，并对浅海声压和质点振速的噪声强度在深度和频率上的变化特性进行仿真分析。最后，对比了系统自噪声谱级和海洋环境噪声谱级，分频段讨论了各个通道的系统自噪声对矢量接收系统的影响。

1 光纤矢量接收系统自噪声特性

矢量水听器作为一种新型的水声测量设备，不仅可以测量声压量，还可以直接、同步测量声场同一点处的质点振速。光纤矢量水听器兼备光纤水听器和矢量水听器两者的优点。

本文所使用的矢量水听器为加速度型光纤矢量水听器，它属于同振式三维矢量水听器。灵敏度是传感器的一项重要性能指标，而且矢量水听器灵敏度直接影响矢量收系统的自噪声特性，下面介绍矢量水听器灵敏度特性。

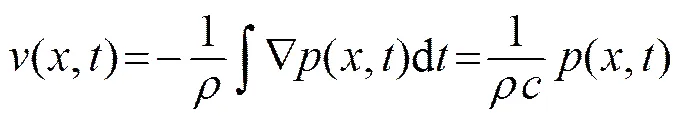
(2)

(3)

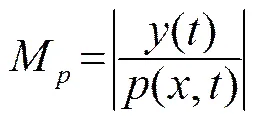
(5)

(6)

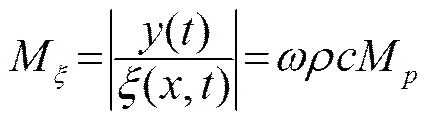
因此，矢量传感器灵敏度之间满足如下关系：

(8)

由式(8)可知，振速型矢量水听器的等效声压灵敏度与频率无关，而加速度型和位移型矢量水听器的等效声压灵敏度具有频率依赖性，加速度型矢量水听器的等效声压灵敏度与频率成正比，位移型矢量水听器的等效声压灵敏度与频率成反比。

对本文中使用的某光纤矢量水听器的灵敏度进行测试，测试频率范围为20 Hz~1 kHz，测试结果如图1~3所示。图1为声压水听器的灵敏度曲线，从图1可知，声压水听器在测试频率范围内灵敏度起伏较小，灵敏度平均值为-147.2 dB ()。图2为三个方向加速度通道的等效声压灵敏度曲线，从图2可知三个方向加速度通道的等效声压灵敏度十分接近，在1 kHz处的等效声压灵敏度约为-155.7 dB（）。图3是根据(8)式折算得到的三个方向加速度通道的加速度灵敏度曲线，从图中可知，X、Y、Z三个通道的平均加速度灵敏度分别为31.6、31.1、31.8 dB (，g表示重力加速度)。

系统自噪声、绕流噪声和构件的低频振动是矢量接收系统的主要干扰，为了保证声场数据记录的有效性，必须将这些干扰的强度控制在一定范围之内。绕流噪声和构件的低频振动都主要集中在低频段。矢量水听器加速度通道的等效声压灵敏度与频率成正比，因而加速度通道自噪声等效声压谱级随频率的降低而增大，这使得自噪声在低频段对矢量接收系统的性能影响较大。

图4为矢量接收系统在安静环境下的自噪声测试结果，图4(a)是各个通道输出光信号的谱级，信号尚未进行灵敏度折算，图4(b)是经灵敏度折算之后的谱级，其中加速度通道噪声已经转化为等效声压谱级。需要说明的是，图中740、1220、1490和2240 Hz处的尖峰并非系统谐振峰，而是测试时环境中存在的干扰，这些尖峰并非一直存在。从图4(a) 中可知，声压通道和加速度通道的自噪声谱级较为接近，并且随频率的变化不明显，只在低频段有较小上升。从图4(b)可知，转换成等效声压之后，声压通道在高于1 kHz频段噪声谱级为36 dB左右，随着频率降低，加速度通道自噪声谱级的上升速度要快于声压通道，并且频率越低，加速度通道自噪声谱级高出声压通道越多。因此，对矢量接收系统低频测量性能影响较大的是加速度通道的系统自噪声，只有把加速度通道的等效声压噪声谱级降低到一定范围，才能保证声场数据的有效记录。

(a) 各个通道输出光信号的谱级

(b)各个通道等效声压谱级

图4 系统自噪声测试结果

Fig.4 Measured results of system self noise spectra

影响矢量接收系统的常见干扰中，绕流噪声可以通过设计流线型框架、增加内外导流罩进行抑制，低频振动干扰也能通过合理的悬置装置和减振措施来加以抑制。下面分析如何降低系统自噪声对光纤矢量水听器接收系统性能的影响。

在实际海洋环境中，声压通道的自噪声谱级往往比海洋环境噪声谱级小，它对接收系统的影响可以忽略，本文不予讨论。为有效记录矢量场数据，必须保证三个方向加速度通道的自噪声等效声压谱级小于海洋环境噪声谱级，即必须满足：

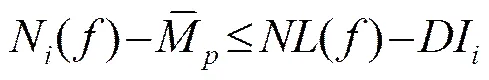
(10)

2 浅海噪声矢量场特性分析

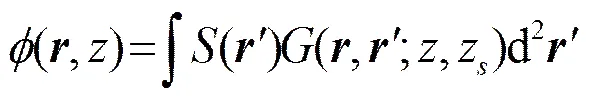
(12)

根据角谱理论可将格林函数展开成格林核函数的积分形式[17]：

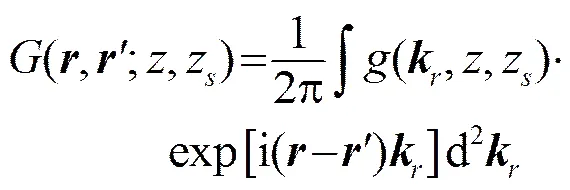
(15)

因此，界面噪声场的声压和质点振速的强度可以表示为

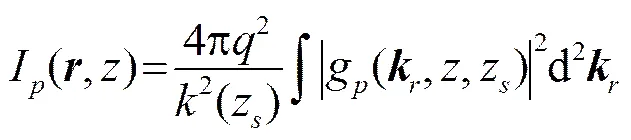
(17)

假设矢量水听器Z轴垂直海面向下，X轴和Y轴与海面平行。根据运动方程和角谱理论不难得出X、Y、Z三个方向的质点振速格林核函数分别为：

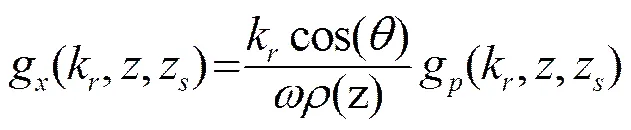
(20)

(21)

(23)

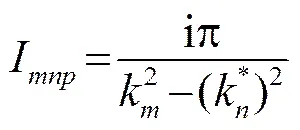
(25)

将X方向振速格林核函数式(19)代入式(17)，可得噪声场的X方向振速强度：

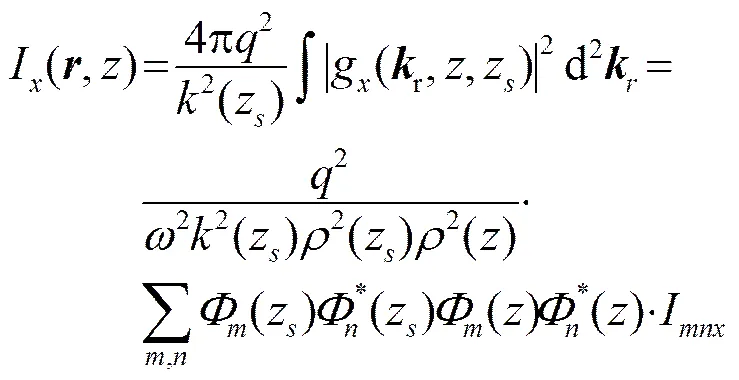
(27)

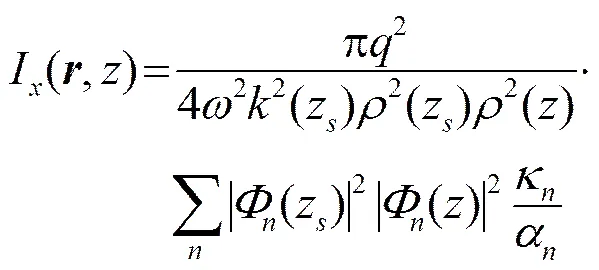
Y方向振速强度的推导与X方向振速强度的推导类似，此处不再重复，且有。

将Z方向振速格林核函数式(21)代入式(17)，可得噪声场的垂直方向的质点振速强度为

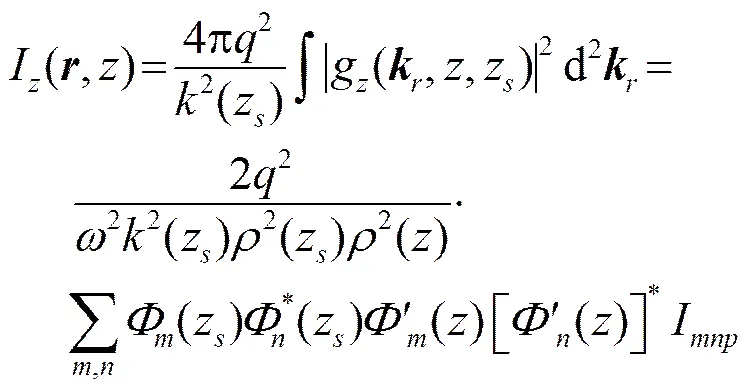
与前面做类似的近似处理，可得

(30)

上面的公式(25)、(28)和(30)组成了非相干海面噪声源情况下声压和三维质点振速的噪声强度简正波计算表达式。

海洋界面噪声与海洋表面风相关，风力激发噪声的机理目前还不十分清楚，其可能的原因有以下几种[19]：(1) 流体静压(一阶效应、二阶效应)；(2) 白浪花及气泡；(3) 浪花溅泼；(4) 湍流伪声；(5) 空气边界层噪声。对于高风速时，后面四项可能是主要机制；对于低风速时，流体静压可能是主要机制，文献[20]根据二阶效应讨论了其机制问题，并得出：

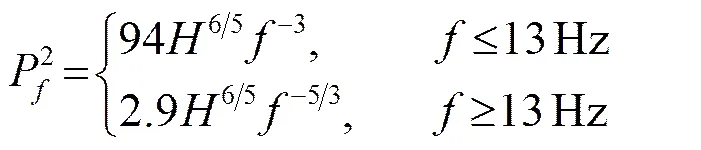
根据前面的噪声矢量场理论，对浅海噪声矢量场的声压和质点振速的强度进行数值仿真，仿真时使用某次矢量水听器海上实验的实测水文，水深为60 m，水体声速剖面如图5所示，海底声速为1600 m/s，海底密度为1.8 g/cm3，海底声吸收为0.25 dB/，噪声场计算频段为100 Hz至1500 Hz。由于X方向和Y方向的质点振速强度相等，因此下面只给出X方向的质点振速强度。

图6为噪声矢量场强度的深度和频率二维伪彩图，其中图6(a)为声压强度，图6(b)为X方向振速强度，图6(c)为垂直振速强度。从图6可以看出，在海面附近声压和X方向振速的强度较弱，垂直振速强度较强；海底附近的声压和X方向振速的强度较大，垂直振速强度较弱；这可以从海面绝对软边界和海底高声阻抗的波导特性得到较好的解释。水体中其他区域除了有小幅度振荡之外，声压和振速的强度随深度和频率变化不大。

图7为1 kHz频点处声压与质点振速的强度特性曲线，其中图7(a)为声压和质点振速的强度随深度的变化曲线，图7(b)为声压与质点振速的噪声强度差随深度的变化曲线。从图7(a)可知，在海面和海底附近声压和质点振速的强度随深度出现振荡，接近海面时声压和X方向振速逐渐减小而垂直振速逐渐增大，接近海底时声压和X方向振速逐渐增大而垂直振速逐渐减小。从图7(b)可知，声压与质点振速的强度差随深度变化较小，X方向振速强度比声压强度小4.8 dB左右，声压与垂直振速的强度差在较浅深度时为5.5 dB左右，在较深深度时为4.8 dB左右。

(a) 声压强度

(b)X方向振速强度

(a) 声压与质点振速的强度曲线

(b)声压与质点振速的强度差曲线

图7 1000 Hz频点处声压与质点振速的强度曲线

Fig.7 Intensity curves of pressure and particle velocities at 1000 Hz

图8为55 m深度处声压与质点振速的强度频率特性曲线，其中图8(a)为声压和质点振速的强度随频率的变化曲线，图8(b)为声压与质点振速的强度差随频率的变化曲线。从图8可知，声压与质点振速的强度随频率变化较小，声压与X方向振速强度差为4.8 dB左右，声压与垂直振速的强度差为4.5 dB左右。再结合式(31)描述的声源功率频率特性可知，浅海噪声矢量场声压和质点振速具有相似的谱斜率，且在低于13 Hz频段谱斜率为-9 dB/倍频程，在高于13 Hz频段谱斜率为-5.3 dB/倍频程，这与著名的Knudson噪声谱级一致。

3 海洋环境噪声矢量场实验结果

2012夏天，中国科学院声学研究所声场声信息国家重点实验室在南海进行了光纤矢量水听器海上实验。光纤矢量接收系统采用座底的方式布放于海底，设备布放点离岸2 km、水深为60 m，传输光缆将矢量水听器和罗经记录的声压、三维加速度和姿态等数据实时地传输到科学研究基站。在海洋环境噪声测量期间，实验海域为三级海况。每个数据文件的记录时间为2 s，本文采用300个数据文件进行能量平均计算环境噪声谱级，实验测得矢量水听器布放点的声速剖面如图5所示。

(a) 声压与质点振速的强度曲线

(b)声压与质点振速的强度差曲线

图8 深度55 m处声压与质点振速的强度曲线

Fig.8 Pressure and particle intensities at depth of 55 m

受海底不平整性和布放等因素的影响，实验中矢量接收系统会有一定程度的倾斜，为控制矢量水听器倾斜程度并记录矢量水听器姿态，矢量接收系统安装了自回转装置和罗经。图9给出了实验期间罗经记录的矢量水听器俯仰角。从图9可知，实验期间矢量水听器俯仰角小于，因此矢量水听器姿态的倾斜对噪声矢量场测量的影响可以忽略。

图10为海洋环境噪声实验测量结果，图中质点振速转换成了等效声压量纲。从图10可知，在高于300 Hz频段，三个通道的质点振速噪声谱级基本一致，都比声压噪声谱级小5 dB左右，且声压和质点振速的噪声谱级具有相似的频率特性，谱斜率皆为-5.3 dB/倍频程，这与前面的理论分析结果一致；在低于300 Hz频段，X通道和Z通道的振速噪声谱级比声压谱级小5 dB左右，而Y通道振速噪声谱级比X和Z通道高3 dB左右，这是因为该频段受航船噪声影响较大，航船噪声相当于环境中离散的相干声源，矢量传播场的水平振速与声压的传播损失接近，矢量水听器在实验布放时X轴平行海岸线，Y轴垂直海岸线指向远处航船密集的区域，因此该频段Y通道振速的噪声谱级有所增加。

图11为海洋环境噪声谱级与系统自噪声谱级对比，各物理量都已转换为声压量纲。图11(a)、图11(b)、图11(c)和图11(d)依次为声压通道、X通道、Y通道和Z通道的测量结果，图中实线为海洋环境噪声谱级，虚线为系统自噪声谱级。从图中可知，除了自噪声测试时存在干扰的频点之外，声压和质点振速的系统自噪声都比环境噪声小。声压通道的自噪声比环境噪声谱级低20 dB左右。X通道自噪声谱级在200 Hz附近与环境噪声谱级最为接近，约比环境噪声低1.5 dB。Y通道和Z通道的自噪声比环境噪声低3.5 dB以上。

(a) 声压通道

(b)X通道

(c)Y通道

(d)Z通道

图11 实测海洋环境噪声与自噪声的谱级对比

Fig.11 The spectra comparison between ambient noise and system noise

4 结论

本文基于简正波理论分析了浅海噪声矢量场声压和质点振速的强度随深度和频率的变化特性。针对声场测量有效性，给出了加速度通道自噪声谱级和灵敏度必须满足的条件，并提出两种降低自噪声对接收系统影响的措施。分析和对比了系统自噪声和海洋环境噪声实测结果。可得出以下结论：

(1) 浅海偶极子界面噪声源激发的噪声矢量场，声压和三维质点振速的谱级具有相似的谱斜率特性，在高于100 Hz频段谱斜率约为-5.3 dB/倍频程。三维质点振速噪声强度基本一致，比声压强度低5 dB左右。

(2) 可以通过降低加速度通道自噪声谱级和提高加速度通道灵敏度两种措施来降低系统自噪声对矢量接收系统的影响，且加速度通道自噪声和灵敏度必须满足式(10)给出的条件。

(3) 对于本文使用的光纤矢量接收系统，声压通道的自噪声谱级比环境噪声低20 dB左右，X通道的自噪声谱级在200 Hz附近与环境噪声谱级最为接近，约比环境噪声低1.5 dB。Y通道和Z通道的自噪声比环境噪声低3.5 dB以上。

[1] 孙贵青, 李启虎. 声矢量传感器研究进展[J].声学学报, 2004, 29(6): 481-490.

SUN Guiqing, LI Qihu. Progress of study on acoustic vector sensor[J]. Acta Acustica, 2004, 29(6): 481-490.

[2] 惠俊英, 刘宏, 余华兵. 声压振速联合信息处理及其物理基础初探[J].声学学报, 2000, 25(4): 303-307.

HUI Junying, LIU Hong, YU Huabing, et al. Study of physical basis of pressure and particle velocity combined processing[J]. Acta Acustica, 2000, 25(4): 303-307.

[3] OLEG E G, YANG D S. On the certain semi- analytical models of low-frequency acoustic fields in terms of scalar-vector description [J]. Chinese Journal of Acoustics, 2004, 23(1): 58-70.

[4] 张海刚, 朴胜春, 杨士莪, 等. 楔形弹性海底声矢量场分布规律研究[J]. 声学学报, 2011, 36(4): 389-395.

ZHANG Haigang, PIAO Shengchun, YANG Shi’e, et al. Researches on the distribution law of vector sound field in elstic wedge bottom.[J]. Acta Acustica, 2011, 36(4): 389-395.

[5] 周士弘. 分层介质波导中的声矢量场传播[J]. 哈尔滨工程大学学报, 2004, 25(1): 38-42.

ZHOU Shi-hong. Acoustic vector fields propagation in horizontal-stratified waveguide [J]. Journal of Harbin Engineering University, 2004, 25(1): 38-42.

[6] DAVID R. Dall’Osto, Peter H Dahl. Properties of the acoustic intensity vector field in a shallow water waveguide[J]. J. Acoust. Soc. Am, 2012, 131(3): 2023 -2035.

[7] Malcolm Hawkes, Arye Nehorai. Acoustic vector sensor correlations in ambient noise[J]. IEEE J. Oceanic Eng, 2001, 26(3): 337-347.

[8] ABDI A, GUO H. Signal correlation modeling in acoustic vector sensor arrays[J]. IEEE Trans Signal Processing, 2009, 57(3): 892-903.

[9] BRUCE M, Abraham. Ambient Noise Measurements with Vector Acoustic Hydrophones[J]. IEEE OCEANS, 2006, 1(4244): 0115-1/06.

[10] 孙贵青, 杨德森, 时胜国. 基于矢量水听器的声压和质点振速的空间相关系数[J]. 声学学报, 2003, 28(6): 509-513.

SUN Guiqing, YANG Desen, SHI Shengguo. Spatial correlation coefficents of acoustic pressure and particle velocity based on vector hydrophone[J]. Acta Acustica, 2003, 28(6): 509-513.

[11] 黄益旺, 李婷, 于盛齐, 等. 水平分层介质表面噪声矢量场空间相关特性[J]. 哈尔滨工程大学学报, 2010, 31(7): 975-981.

HUANG Yiwang, LI Ting, YU Shengqi, et al. Spatial correlation of surface noise received by acoustic vector sensors in a horizontally stratified medium[J]. Journal of Harbin Engineering University, 2010, 31(7): 975-981.

[12] Arye Nehorai, Eytan Paldi. Acoustic Vector-Sensor Array Processing[J]. IEEE Trans. Signal Processing, 1994, 42(9): 2481-2491.

[13] Malcolm Hawkes, Arye Nehorai. Acoustic vector sensor array processing in the presence of a reflecting boundary[J]. IEEE Trans. Signal Processing, 2000, 48(11): 2981-2993.

[14] 牛嗣亮, 张振宇，胡永明, 等. 单矢量水听器的姿态修正测向问题探讨[J]. 国防科技大学学报, 2011, 33(6): 105-110.

NIU Siliang, ZHANG Zhenyu, HU Yongming, et al. Direction of arrival estimation from a single vector hydrophone with attitude correction[J]. Journal of National University of Defense Technology, 2011, 33(6): 105-110.

[15] Malcolm Hawkes, Arye Nehorai. Acoustic vector sensor beamforming and Capon direction estimation[J]. IEEE Oceanic Eng, 1998, 46(9): 2291–2304.

[16] 李风华, 孙梅, 张仁和. 由矢量水听器阵反演海底地声参数[J]. 哈尔滨工程大学学报, 2010, 31(7): 895-902.

LI Fenghua, SUN Mei, ZHANG Renhe. Geo-acoustic inversion for a vector sensor array[J]. Journal of Harbin Engineering University, 2010, 31(7): 895-902.

[17] JENSEN F B, KUPERMAN W A, PORTER M B, et al. Computational ocean acoustics[M]. New York: American Institute of Physics, 1994.

[18] KUPERMAN W A, INGENITO F. Spatial correlation of surface generated noise in a stratified ocean[J]. J. Acoust. Soc. Am, 1980, 67(6): 1988-1996.

[19] 汪德昭, 尚尔昌. 水声学[M]. 2版. 北京：科学出版社, 2013: 303-319.

WANG Dezhao, SHANG Erchang. Underwater Acoustics[M]. 2nd Edition. Beijing: Science Press, 2013:303-319.

[20] MARSH H W. Origin of the knudson spectra[J]. J. Acoust. Soc. Am, 1963, 35(1): 409.

[21] WILLIAM M. Carey, RICHARD B Evans, JAMES A Davis, et al. Deepocean vertical noise directionality[J]. IEEE Oceanic Eng, 1990, 15(4): 324-334.

Study of vector noise field characteristics in shallow water by fiber optical vector hydrophone

ZHU Liang-ming1,2, LI Feng-hua2, CHEN De-sheng1

(1. State Key Laboratory of Acoustics, Institute of Acoustics, Chinese Academy of Sciences, Beijing 100190, China;2. College of Physics, University of Chinese Academy of Sciences, Beijing 100049, China)

Vector noise field characteristics in shallow water are analyzed with normal mode theory, and the intensity distributionsof pressure and particle velocities in shallow water vector noise field are simulated, which are well in agreement with experiment results. The expressions of system noise intensity and sensitivity, which meetthe validity of data record, are presented, and two methods of suppressing the influence of system noise on fiber-optical vector hydrophone system are also proposed. System noise and ambient noise are tested with the fiber-optical vector hydrophone system, and analyzed indifferent frequency bands. The result shows that the self-noise spectrum level in pressure channel is 20 dB lower than ambient noise level, and the self-noise spectrum levels in Y and Z acceleration channels are lower than ambient noise level by 3.5 dB more. While the self-noise spectrum level in X acceleration channel is nearestto ambient noise level at 200 Hz (about 1.5 dB lower).

fiber-optical vector hydrophone; vector noise field; system noise; sensitivity

TB556

A

1000-3630(2016)-02-0101-08

10.16300/j.cnki.1000-3630.2016.02.004

2015-02-06;

2015-04-20

国家自然科学基金资助项目(11125420)。

朱良明(1988－), 男, 江西赣州人, 博士, 研究方向为海洋声学、矢量水听器声信号处理。

李风华, E-mail: lfh@mail.ioa.ac.cn。