河流截面流量与速度水位关系的拟合研究

毕凤美，彭东立，许伟杰



河流截面流量与速度水位关系的拟合研究

毕凤美，彭东立，许伟杰

(中国科学院声学研究所东海研究站，上海200032)

基于声学多普勒流速剖面仪测得的不同水位河流截面的平均流速，研究了走航式宽带声学多普勒流量测量系统中，流量与速度水位关系的拟合表达式。采用窄深矩形截面和梯形截面流速分布模型，结合声学多普勒流速剖面仪求得不同水位下的平均流速值，在MATLAB平台下，对两种不同截面中流量与速度水位关系进行了拟合,并求得均方根误差检验拟合的精度。仿真结果表明：通过走航式宽带声学多普勒流量测量算法求得的河流截面流量，与由流速分布模型求得的流量真值间的误差，满足单次流量测验允许的误差要求，表明给出的流量与速度水位关系拟合公式能够较好地表现河流截面的流量变化趋势。对于天然明渠流量推算具有重要的参考价值。

流量与速度水位关系；声学多普勒流速剖面仪；拟合公式；均方根误差

0 引言

在水文测验中，流量与速度水位关系的确定能为流量预报、灌溉区以及水库水量调度提供重要的依据。应用幂指数描述水位流量关系的传统方法,因其求解过程的缺陷性,使得利用最小二乘法确定的参数只能使变换后方程的残差平方和最小,而不能保证原始方程的残差平方和最小[1]。故不能保证所拟合的水位流量关系曲线为最优拟合曲线。同时，该方法没有对拟合精度进行检测，研究成果的可靠性难以得到保证。

本文在前人研究的基础上，采用胡云进等[2-3]的窄深矩形截面和梯形截面流速分布数学模型，得到了不同河流截面的流速分布，再利用流速面积法求得河流截面的流量，将其作为流量真值，结合走航式宽带声学多普勒流量测量算法得到的不同水位下对应的微断面中部实测区的平均流速值，在MATLAB仿真平台上，对两种不同形状河流截面中流量与速度水位关系进行了多项式拟合，求解出矩形河流截面明渠和梯形河流截面明渠中流量与速度水位关系的多项式拟合公式，并得到水位、河流截面平均流速、流量关系的三维曲面。最后用均方根误差对拟合效果进行了检测，保证了研究成果的可信度。该研究对水库库容区及河渠流量的分析、监测将产生重要的应用价值。

1 河流截面流速分布数学模型

目前，明渠河流截面流量测量方法有多种，如流速面积法、堰槽法、动船法、水位流量关系法等。无论采用何种方法，要保证河流截面流量的测量精度，必须准确掌握河流截面的流速分布。随着有关窄深矩形截面、梯形截面等明渠流速分布理论研究的不断深入和发展, 本文采用胡云进等[2-3]经过建模并用实验资料验证了的流速分布模型来模拟河流截面的流速分布。

1.1 垂线平均流速横向分布律

通过对河流截面明渠流速分布的大量仿真实验，结果表明：受两边壁的影响，垂线平均流速沿横向的分布，在两边壁附近变化幅度较大，离边壁一定距离后，变化幅度较小，最终基本保持不变，中垂线处平均流速最大[2]。选择幂函数公式描述河流截面垂线平均流速沿横向的分布。矩形截面垂线平均流速横向分布为

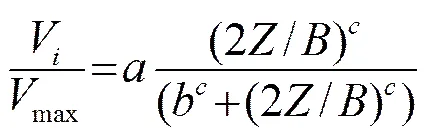
梯形截面垂线平均流速横向分布为

(2)

1.2 垂线流速分布律[2-3]

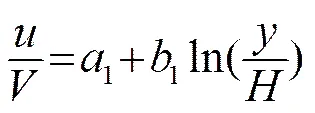
(4)

用乘幂公式描述梯形河流截面外区的垂线流速分布：

2 宽带声学多普勒流量测量算法

声学多普勒流量测量原理和传统的流速仪法相同，但走航式宽带声学多普勒流量测量是动态方法，不要求测流截面垂直于河岸，在走航过程中采样率高，可以将整个河流截面沿河宽方向划分为更小的子截面，具有不扰动流场、省时省工的优点。

声学多普勒流速剖面仪(Acoustic Doppler Current Profiler，ADCP)进行河流截面流量测验时，总流量的计算由四部分组成：中部实测区、表层未测区、底部“旁瓣”影响区和左右岸边区域。除中部实测区外，其他三个区域的流速和流量均需通过中部实测区数据外延来估算。

2.1 中部实测区流量计算[4]

ADCP可以直接测出中部实测区每一个微断面内的平均流速，其值是所有有效单元流速之和的平均。方向分量(方向的类似)可表示为

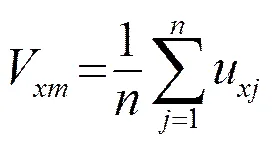
对应于ADCP走航测验起点至终点之间河流截面的中部流量可表示为：

(7)

2.2 表层和底层流量计算

借助于幂指数流速剖面的假定来计算表层和底层的平均流速和流量[4]。微断面内表层平均流速方向的分量(方向的类似)计算公式为

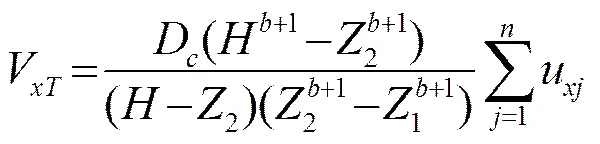
式中：是水深，单位：m；是幂指数，常取1/6。

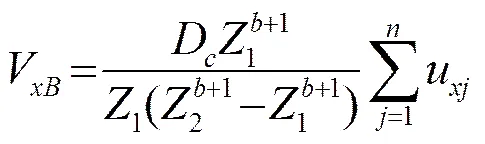
对应于ADCP走航测验起点到终点之间河流截面的表层流量为

(10)

底层流量为

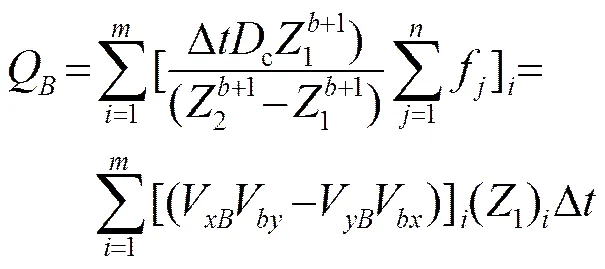
2.3 岸边流量估计

根据走航式ADCP流量测量的原理，岸边区域属于非实测区，可由经验公式[5]来计算流量：

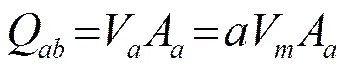
按照中华人民共和国水利部《河流流量测验规范》，岸边流速系数式[6]的取值如表1所示。

表1 岸边流速系数列表

3 模型仿真结果及分析

利用第1节中提到的河流截面流速分布模型，对不同（主要指流速分布和水位不同）的矩形截面和梯形截面分别进行了数值模拟，求出各个小微断面内的平均流速值，然后利用流速面积法求出整个河流截面的总流量，将其作为流量测量的真值，最后根据ADCP流量测量算法算出不同河流截面的流量并与真值作误差分析。

3.1 矩形截面数值仿真

3.1.1 真值的仿真过程

将设定的参数分别代入式(1)、(3)、(4)中，可求得各个小微断面内的测点流速。

对水位分别为5、6、8、9 m的河流截面进行了数值模拟。以每个小微断面几何中点处的水流速作为该微断面内的平均流速，用该流速乘以各个小微断面的面积即为该微断面内的流量，所有流量的代数和即为矩形河流截面的流量真值。

3.1.2 ADCP测量算法求解矩形截面流量过程

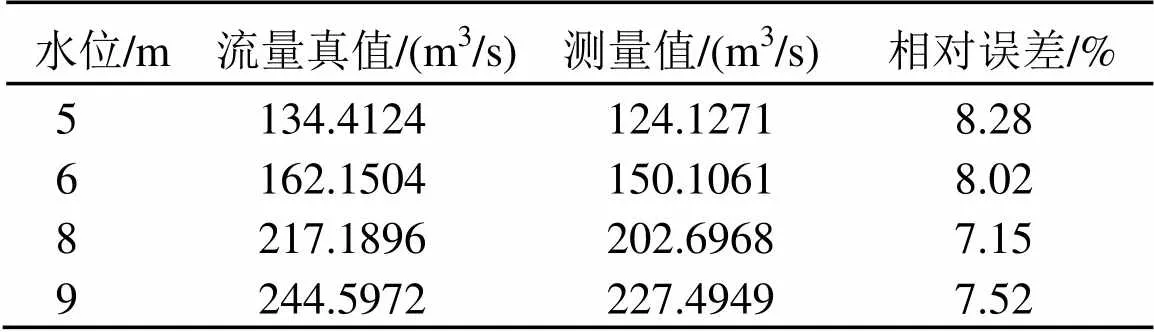
表2 矩形截面ADCP测量结果与真值对比

3.2 梯形截面数值仿真

3.2.1 真值的仿真过程

设定河流截面宽为23.4 m，糙率=0.014，边坡比是1:1，中垂线上的最大平均流速是1.5 m/s。沿着河流截面方向上，第一条测速垂线距离左岸边2.7 m，之后每隔3 m设置一条测速垂线，最后一条测速垂线距离右岸边2.7 m，测速垂线共9条。根据文献[3]，相关的仿真参数设置如下：

将设置的参数分别代入到式(2)、(3)、(5)中，可求得各个小微断面内的水流速。

对水位分别为7.2、9.36、10.4 m的河流截面进行了数值模拟。以每个小微断面几何中点处的水流速作为该微断面内的平均流速，用该流速值乘以微断面的面积即为各微断面内的流量，所有流量的代数和即为梯形河流截面的流量真值。

3.2.2 ADCP测量算法求解梯形截面流量过程

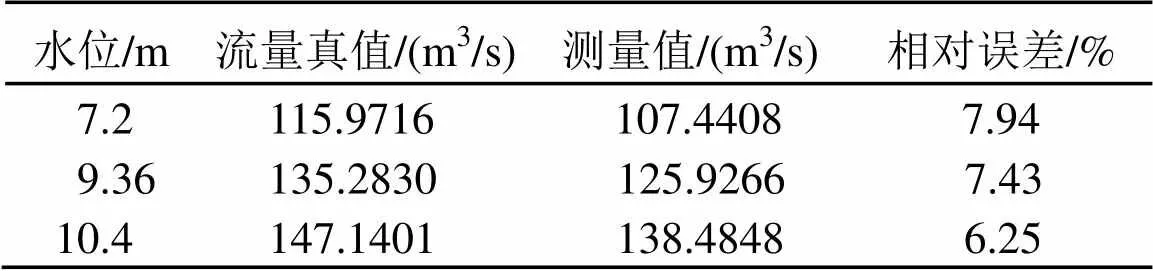
表3 梯形截面ADCP测量结果与真值对比

通过误差分析可知：对于不同水位的矩形截面和梯形截面，用ADCP进行走航式流量测量的结果与流量真值的相对误差均满足单次流量测验允许的误差要求[6]。

4 流量与速度水位关系的拟合公式

河流截面中流量与速度水位的关系，可以通过各个深度微断面中的平均流速与面积的乘积来表示。对于矩形河流截面和梯形河流截面，由于是比较规则的几何形状，很容易用数学表达式表示各个深度微断面的面积。各个深度微断面中的平均流速可以表示成关于水位和ADCP测得的中部实测区平均流速的函数。

下面将利用ADCP流量测量算法求得的实测区各个深度微断面中的平均流速值、水位以及通过流速分布模型求得的河流截面流量真值，在MATLAB平台下使用曲线拟合工具箱进行多项式拟合，得到流量与速度水位关系的拟合表达式，并得到了河流截面三维拟合曲面图。

4.1 矩形截面流量与速度水位关系的拟合公式

表4是利用ADCP流量测量算法求得的矩形截面中部实测区对应水位处的平均流速和河流截面流量真值的数值列表。根据表4中的数据，在MATLAB平台下拟合出矩形河流截面的流量与速度水位关系表达式，得到三维拟合曲面，并求解出拟合多项式的均方根误差(Root Mean Square Error，RMSE)。

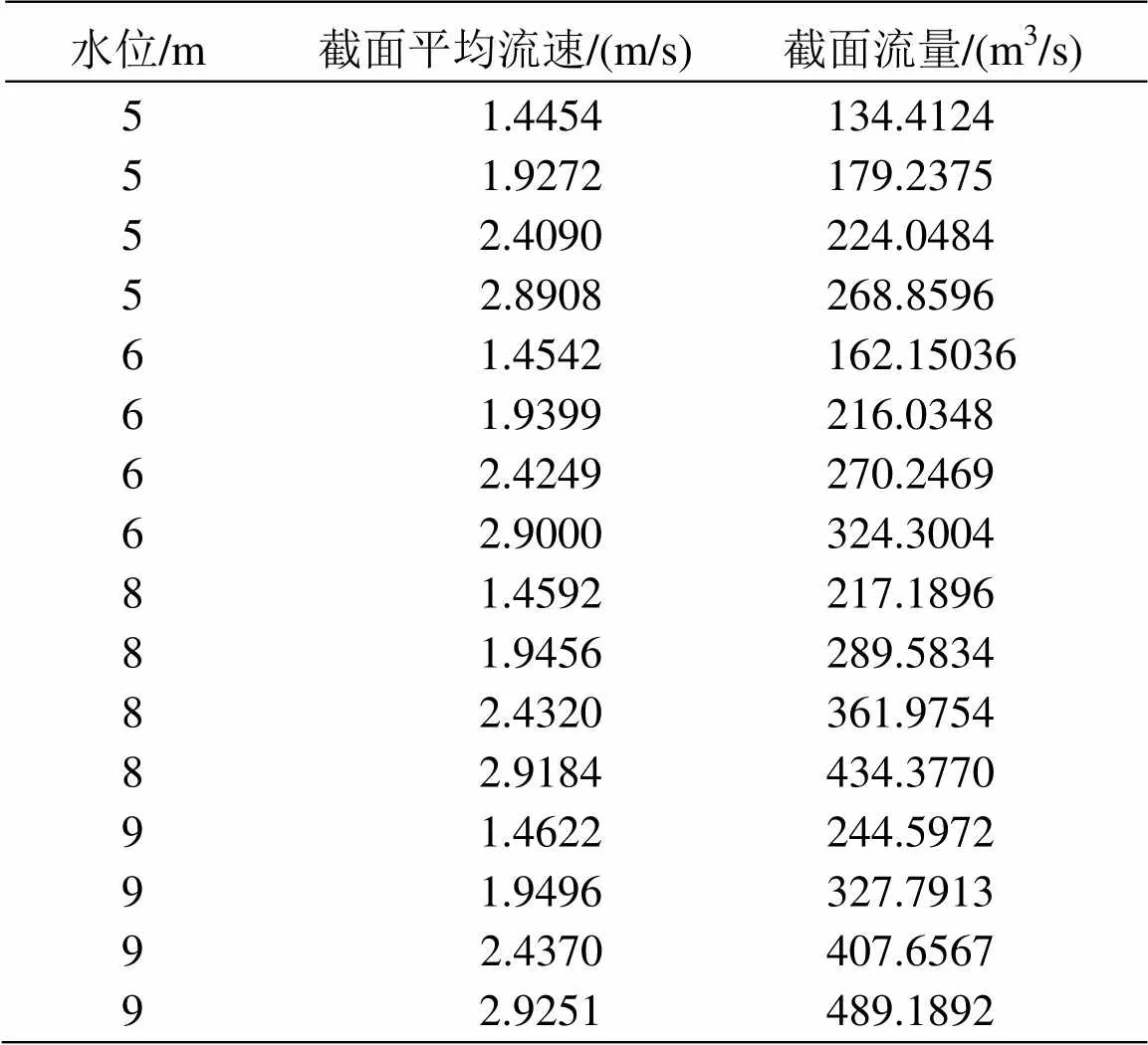
表4 矩形截面的水位、流速和流量数值列表

经过拟合得到的矩形截面流量与速度水位关系的拟合表达式为

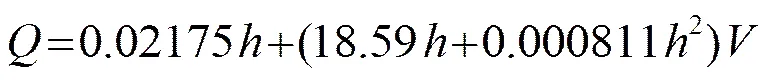
图1是拟合得到的矩形河流截面的三维拟合曲面。

4.2 梯形截面流量与速度水位关系的拟合公式

表5是利用ADCP流量测量算法求得的梯形截面中部实测区对应水位处的平均流速和河流截面流量真值的数值列表。根据表5中数据，在MATLAB平台下拟合出梯形截面的流量与速度水位关系表达式，得到河流截面的三维拟合曲面，并求得拟合多项式的均方根误差值。

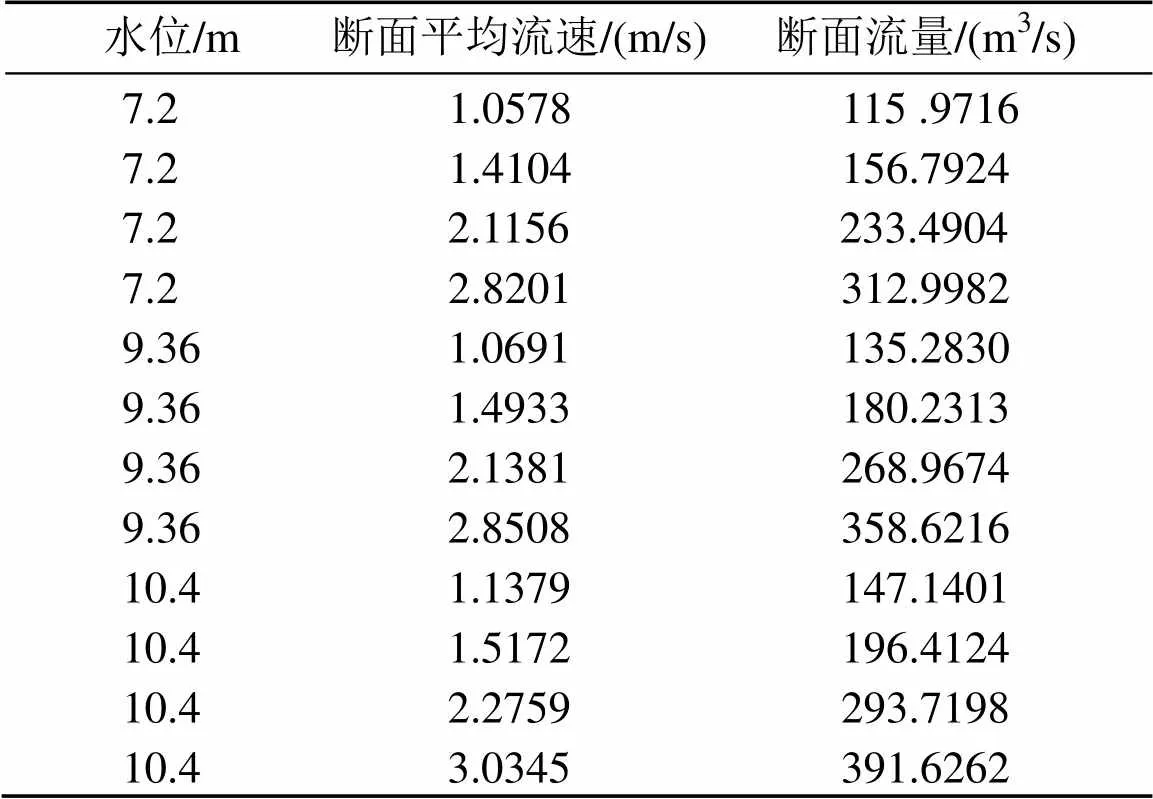
表5 梯形断面的水位、流速和流量数值列表

经过拟合得到的梯形河流截面流量与速度水位关系的拟合表达式是：

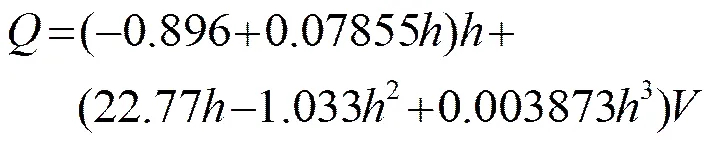
同时得到多项式拟合公式的RMSE=2.7。图2是经拟合得到的梯形河流截面的三维拟合曲面。

三维拟合曲面可直观地表现河流截面流量与速度水位的关系。通过均方根误差的分析可得：对于两种不同形状的河流截面，通过曲线拟合工具得到的流量与速度水位的拟合多项式都能很好地表现矩形河流截面和梯形河流截面的流量变化趋势。

5 结论

本文研究了窄深矩形和梯形河流截面中流量与速度、水位的拟合关系，求解出河流截面的关系拟合公式，得到窄深矩形和梯形两种河流截面的三维拟合曲面。在今后的实际应用中，只需使用声学多普勒流速剖面仪在河流截面进行走航测验，利用测得的平均流速和水位值即可推算出整个河流截面的流量。本文对于河流截面和水库的水量调配和分析将提供很好的帮助。

[1] 周世良, 尚明芳, 李怡, 等. 拉格朗日乘子法在水位流量关系拟合中的应用[J]. 水文, 2011, 31(5): 15-17.

ZHOU Shiliang, SHANG Mingfang, LI Yi, et al. Application of lagrange multiplier method in fitting stage-discharge relation [J]. Journal of China Hydrology, 2011, 31(5): 15-17.

[2] 胡云进, 万五一，蔡甫款, 等. 窄深矩形断面明渠流速分布的研究[J]. 浙江大学学报: 工学版, 2008, 42(1): 183-187.

HU Yunjin, WAN Wuyi. CAI Fukuan, et al. Velocity distribution in narrow and deep rectangular open channels[J]. Journal of Zhejiang University: Engineering Science, 2008, 42(1): 183-187.

[3] 胡云进, 郜会彩, 耿洛桑, 等. 梯形断面明渠流速分布的研究[J]. 浙江大学学报: 工学版, 2009, 43(6): 1102-1106.

HU Yunjin, GAO Huicai, GENG Luosang, et al. Laws of velocity distribution in trapezoidal open channels[J]. Journal of Zhejiang University: Engineering Science, 2009, 43(6): 1102-1106.

[4] 田淳, 刘少华. 声学多普勒测流原理及其应用[M]. 郑州: 黄河水利出版社, 2003: 191-192.

TIAN Chun, LIU Shaohua. The principle and application of acoustic Doppler discharge measurements[M]. Zhengzhou: The Yellow River Water Conservancy Press, 2003: 191-192.

[5] Simposon M R. Discharge measurements using a broad-band acoustic Doppler current profiler[R]. Sacramento, California: Charles G. Groat, 2001.

[6] 中华人民共和国水利部, SL337-2006, 声学多普勒流量测验规范[S]. 中国水利水电出版社, 2006.

Ministry of Water Resources of the People’s Republic of China. Code for discharge measurement of acoustic Doppler current profiler[S]. China Water & Power Press, 2006.

Research on relation fitting formula of river section discharge versus velocity and water level

BI Feng-mei, PENG Dong-li, XU Wei-jie

(Shanghai Acoustic Laboratory, Institution of Acoustic, Chinese Academy of Sciences, Shanghai 200032, China)

This paper studies the relation fitting formula of discharge versus velocity and water level based on the average-velocity values calculated by acoustic Doppler current profilerat different water depth. The narrow and deep rectangular and trapezoidal cross-section velocity distribution models are adopted. Combined with the average-velocity values at different water depths calculated by broad-band ADCP, the fitting for discharge versus velocity and water level is made on the MATLAB platform for two different river cross-sections. This paper obtains a polynomial fitting formula of discharge versus velocity and water level, and meanwhile the accuracy of fitting is tested through root mean square error. Simulation results show that the error between the discharge values calculated by the underway broad-band acoustic Doppler discharge measurement algorithm and the discharge true-values calculated by velocity distribution model satisfies the tolerance requirements of single discharge test. The relation fitting formula of discharge versus velocity and water level can reflect the changing trends of river cross-section.This paper has an important reference value for the river-section discharge calculation of open channel.

discharge versus velocity and water level;Acoustic Doppler Current Profiler; fitting formula; root mean square error

TB533

A

1000-3630(2016)-02-0120-05

10.16300/j.cnki.1000-3630.2016.02.007

2015-03-04;

2015-06-10

毕凤美(1988－), 女, 山东莱芜人, 硕士研究生, 研究方向为信号与信息处理。

毕凤美, E-mail: bifengmei@126.com